机器学习笔记之高斯网络(一)基本介绍
机器学习笔记之高斯网络——基本介绍
- 引言
-
- 回顾:
-
- 条件独立性
- 概率图模型
- 高斯网络
-
- 高斯网络介绍
- 高斯网络的条件独立性
-
- 随机变量之间的边缘独立
- 随机变量之间的条件独立
引言
本节将介绍高斯网络
回顾:
条件独立性
在概率图模型——背景介绍中介绍了条件独立性,条件独立性的核心思想是:给定某随机变量集合 X A \mathcal X_{\mathcal A} XA的条件下,可能存在随机变量集合 X B , X C \mathcal X_{\mathcal B},\mathcal X_{\mathcal C} XB,XC内部结点之间存在关联,但 X B , X C \mathcal X_{\mathcal B},\mathcal X_{\mathcal C} XB,XC之间不存在关联:
X B ⊥ X C ∣ X A \mathcal X_{\mathcal B} \perp \mathcal X_{\mathcal C} \mid \mathcal X_{\mathcal A} XB⊥XC∣XA
并且 X A , X B , X C \mathcal X_{\mathcal A},\mathcal X_{\mathcal B},\mathcal X_{\mathcal C} XA,XB,XC是三个不相交的特征集合。
概率图模型
在概率图模型——背景介绍中介绍了概率图模型(Probabilisitc Graphical Model,PGM)。从图的表示角度观察,它可以分为有向图和无向图两种:
-
基于有向图的概率图模型又称贝叶斯网络(Bayesian Network),也称信念网络(Belief Network)。
从条件独立性的角度观察,贝叶斯网络的条件独立性表达包含三种经典情况:- 同父结构(Common Parent),对应概率图结构表示如下:
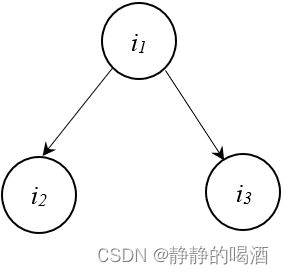
上图结构表现的现象是:给定结点 i 1 i_1 i1的取值,结点 i 2 , i 3 i_2,i_3 i2,i3条件独立。
i 2 ⊥ i 3 ∣ i 1 i_2 \perp i_3 \mid i_1 i2⊥i3∣i1 - 顺序结构(Sequence),对应概率图结构表示如下:

上图结构表现的现象是:给定结点 i 2 i_2 i2的取值,结点 i 1 , i 3 i_1,i_3 i1,i3相互独立。
i 1 ⊥ i 3 ∣ i 2 i_1 \perp i_3 \mid i_2 i1⊥i3∣i2 - V \mathcal V V型结构(V-Structure),对应概率图结构表示如下:
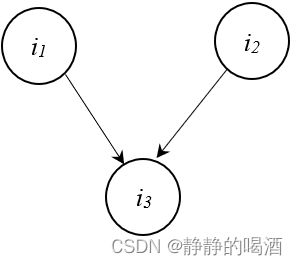
该结构表现的现象是:给定 i 3 i_3 i3结点的条件下, i 1 , i 2 i_1,i_2 i1,i2必不独立;相反, i 3 i_3 i3取值未知的条件下, i 1 , i 2 i_1,i_2 i1,i2相互独立。
i 3 ∣ i 1 ⊥ i 2 i_3 \mid i_1 \perp i_2 i3∣i1⊥i2
- 同父结构(Common Parent),对应概率图结构表示如下:
-
基于无向图的概率图模型又称马尔可夫网络(Markov Network),也称马尔可夫随机场(Markov Random Field)。
相比于贝叶斯网络,马尔可夫随机场中描述变量之间的依赖关系 仅包含一种格式:

该结构表现的现象是:给定 i 1 i_1 i1结点的条件下,结点 i 2 , i 3 i_2,i_3 i2,i3相互独立。
i 2 ⊥ i 3 ∣ i 1 i_2 \perp i_3 \mid i_1 i2⊥i3∣i1
高斯网络
高斯网络介绍
高斯网络(Gaussian Network),又称高斯概率图模型(Gaussian Probabilistic Graphical Model)。它同样也是一种概率图模型。
从随机变量的类型角度观察,将随机变量分为离散型随机变量核连续型随机变量两种。已经介绍的随机变量是离散型随机变量的有:
- 高斯混合模型(Gaussian Mixture Model,GMM),其隐变量 Z \mathcal Z Z包含离散的 ∣ K ∣ |\mathcal K| ∣K∣个取值,每个取值条件下的观测变量服从高斯分布:
P ( X ) = ∑ k = 1 K α k ⋅ N ( μ k , Σ k ) ∑ k = 1 K α k = 1 \mathcal P(\mathcal X) = \sum_{k=1}^{\mathcal K} \alpha_k \cdot \mathcal N(\mu_{k},\Sigma_k) \quad \sum_{k=1}^{\mathcal K} \alpha_k = 1 P(X)=k=1∑Kαk⋅N(μk,Σk)k=1∑Kαk=1 - 隐马尔可夫模型(Hidden Markov Model,HMM):隐变量 I \mathcal I I是离散型随机变量,观测变量 O \mathcal O O没有要求。
- 条件随机场(Condition Random Field,CRF):隐变量 I \mathcal I I是离散型随机变量,观测变量 O 1 : T \mathcal O_{1:T} O1:T常以序列形式出现。
而高斯网络是随机变量是连续型随机变量 的一种代表模型,其核心思想是:随机变量都是连续型随机变量,并且随机变量服从高斯分布。同上,根据图的表示,高斯网络同样分为有向图和无向图两种表达形式:
- 高斯贝叶斯网络(Gaussian Beyasian Network,GBN)
- 高斯马尔可夫网络(Gaussian Markov Network,GMN)
高斯网络的条件独立性
假设一个高斯图模型表示如下:
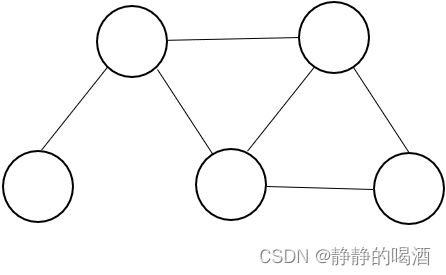
这只是一个简单的马尔可夫网络,并且每个结点都是一个一维随机变量。这里的随机变量均是连续型随机变量,并且均服从高斯分布:
x i ∼ N ( μ i , Σ i ) x_i \sim \mathcal N(\mu_i,\Sigma_i) xi∼N(μi,Σi)
假设随机变量集合的维数是 p p p,整个高斯图模型中所有随机变量对应的概率密度函数 P ( X ) \mathcal P(\mathcal X) P(X)表示为:
X = ( x 1 , x 2 , ⋯ , x p ) T P ( X ) = 1 ( 2 π ) p 2 ∣ Σ ∣ 1 2 exp [ − 1 2 ( x − μ ) T Σ − 1 ( x − μ ) ] \begin{aligned} \mathcal X & = (x_1,x_2,\cdots,x_p)^T \\ \mathcal P(\mathcal X) & = \frac{1}{(2\pi)^{\frac{p}{2}}|\Sigma|^{\frac{1}{2}}} \exp \left[-\frac{1}{2} (x - \mu)^T \Sigma^{-1}(x - \mu)\right] \end{aligned} XP(X)=(x1,x2,⋯,xp)T=(2π)2p∣Σ∣211exp[−21(x−μ)TΣ−1(x−μ)]
这明显是一个多元高斯分布。一个高斯图模型和一个多元高斯分布存在映射关系。其中 μ \mu μ表示多元高斯分布的期望, Σ \Sigma Σ表示多元高斯分布的协方差矩阵。
其中,期望 μ \mu μ表示为:
μ = [ μ i ] p × 1 = ( μ 1 μ 2 ⋮ μ p ) p × 1 \mu = [\mu_i]_{p \times 1} = \begin{pmatrix} \mu_1 \\ \mu_2 \\ \vdots \\ \mu_p \end{pmatrix}_{p \times 1} μ=[μi]p×1=⎝⎜⎜⎜⎛μ1μ2⋮μp⎠⎟⎟⎟⎞p×1
协方差矩阵 Σ \Sigma Σ表示为:
Σ = [ σ i j ] p × p = ( σ 11 , σ 12 , ⋯ , σ 1 p σ 21 , σ 22 , ⋯ , σ 2 p ⋮ σ p 1 , σ p 2 , ⋯ , σ p p ) p × p \Sigma = [\sigma_{ij}]_{p \times p} = \begin{pmatrix} \sigma_{11},\sigma_{12},\cdots,\sigma_{1p} \\ \sigma_{21},\sigma_{22},\cdots,\sigma_{2p} \\ \vdots \\ \sigma_{p1},\sigma_{p2},\cdots,\sigma_{pp} \\ \end{pmatrix}_{p \times p} Σ=[σij]p×p=⎝⎜⎜⎜⎛σ11,σ12,⋯,σ1pσ21,σ22,⋯,σ2p⋮σp1,σp2,⋯,σpp⎠⎟⎟⎟⎞p×p
其中 σ i j \sigma_{ij} σij表示随机变量 x i , x j x_i,x_j xi,xj的协方差结果:
这里没有写成 ( x i − μ i ) ( x j − μ j ) T (x_i - \mu_i)(x_j - \mu_j)^T (xi−μi)(xj−μj)T因为已经设定的一维随机变量。
σ i j = C o v ( x i , x j ) = E [ ( x i − μ i ) ( x j − μ j ) ] \sigma_{ij} = Cov(x_i,x_j) = \mathbb E\left[(x_i - \mu_i)(x_j - \mu_j)\right] σij=Cov(xi,xj)=E[(xi−μi)(xj−μj)]
随机变量之间的边缘独立
根据协方差的定义,如果在同一物理量纲(基准)的条件下, C o v ( x i , x j ) = 0 Cov(x_i,x_j) = 0 Cov(xi,xj)=0,那个称随机变量 x i , x j x_i,x_j xi,xj是不相关的。从独立性的角度观察,即 x i , x j x_i,x_j xi,xj相互独立:
这个相互独立意味着 x i x_i xi和 x j x_j xj在不观察其他变量的条件下是‘边缘独立/绝对独立’的,这种独立在现实世界的问题中并不常见。
σ i j = 0 ⇒ x i ⊥ x j σ i j = 0 ⇒ P ( x i , x j ) = P ( x i ) P ( x j ) \begin{aligned} \sigma_{ij} = 0 & \Rightarrow x_i \perp x_j \\ \sigma_{ij} = 0 & \Rightarrow \mathcal P(x_i,x_j) = \mathcal P(x_i)\mathcal P(x_j) \end{aligned} σij=0σij=0⇒xi⊥xj⇒P(xi,xj)=P(xi)P(xj)
如果两个随机变量之间的基准存在差异,对应的 σ i j \sigma_{ij} σij也可能存在很大差异。为此可以引入相关系数(Correlation Coefficient):
ρ i j = C o v ( x i , x j ) D ( x i ) D ( x j ) = σ i j σ i i σ j j \begin{aligned} \rho_{ij} & = \frac{Cov(x_i,x_j)}{\sqrt{\mathcal D(x_i)}\sqrt{\mathcal D(x_j)}} \\ & = \frac{\sigma_{ij}}{\sqrt{\sigma_{ii}\sigma_{jj}}} \end{aligned} ρij=D(xi)D(xj)Cov(xi,xj)=σiiσjjσij
如果相关系数 ρ i j = 0 \rho_{ij} = 0 ρij=0称 x i , x j x_i,x_j xi,xj不相关。
随机变量之间的条件独立
条件独立性本质上是为了简化运算提出的一种假设,从而在概率图模型中得到映射。
关于高斯网络的条件独立性,引入一个概念:精度矩阵(Precision Matrix),也称作 信息矩阵(Information Matrix)。它是协方差矩阵的逆矩阵:
第一次遇到‘精度矩阵’是在推断任务之边缘概率分布与条件概率分布,记录一下时间点~
Λ = Σ − 1 = ( λ 11 , λ 12 , ⋯ , λ 1 p λ 21 , λ 22 , ⋯ , λ 2 p ⋮ λ p 1 , λ p 2 , ⋯ , λ p p ) p × p \Lambda = \Sigma^{-1} = \begin{pmatrix} \lambda_{11},\lambda_{12},\cdots,\lambda_{1p} \\ \lambda_{21},\lambda_{22},\cdots,\lambda_{2p} \\ \vdots \\ \lambda_{p1},\lambda_{p2},\cdots,\lambda_{pp} \\ \end{pmatrix}_{p \times p} Λ=Σ−1=⎝⎜⎜⎜⎛λ11,λ12,⋯,λ1pλ21,λ22,⋯,λ2p⋮λp1,λp2,⋯,λpp⎠⎟⎟⎟⎞p×p
关于精度矩阵 Λ \Lambda Λ与条件独立性的关联关系表示如下:
其中 x − i − j x_{-i-j} x−i−j表示随机变量集合 X \mathcal X X中除去 x i , x j x_i,x_j xi,xj之外的其他随机变量。
λ i j = 0 ⇔ x i ⊥ x j ∣ x − i − j \lambda_{ij} = 0 \Leftrightarrow x_i \perp x_j \mid x_{-i-j} λij=0⇔xi⊥xj∣x−i−j
精度矩阵的核心在于:精度矩阵中的元素与条件独立性(概率图的映射)紧密结合在一起。
下一节将介绍高斯贝叶斯网络。
相关参考:
高斯图模型、精度矩阵、偏相关系数、贝叶斯估计(利用贝叶斯做数据融合)、Wishart分布和逆Wishart分布
协方差——百度百科
概率图模型(四):经典概率图模型
机器学习-高斯网络(1)-总体介绍