NNDL 作业3:分别使用numpy和pytorch实现FNN例题
1.过程推导 - 了解BP原理
神经网络结构如下图所示,总体上由三部分组成:输入层、隐藏层(为方便起见,图中给出一层,实际中可以有多层)和输出层。对于每一层,都是由若干个单元(神经元)组成。相邻两层的神经元之间是全连接的,但是同一层内,各神经元之间无连接。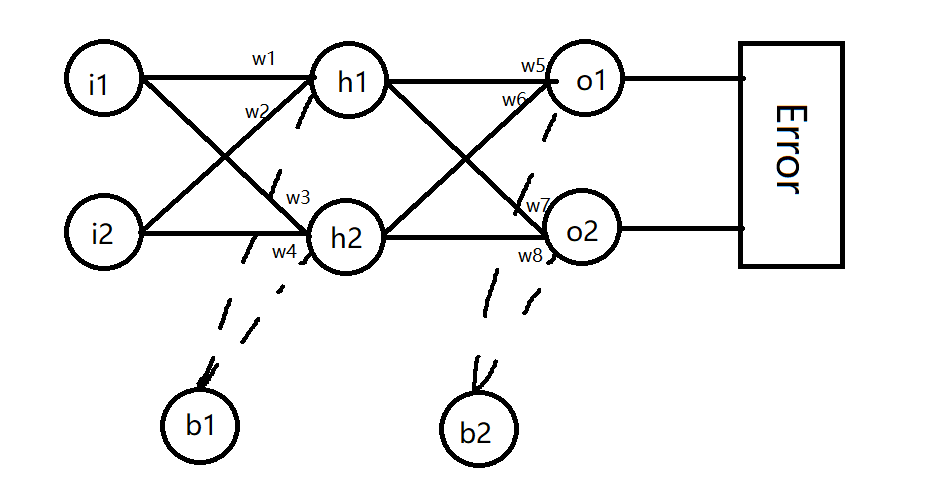
这是一个简单的神经网络。
正向传播:输入层——隐藏层
![]()
![]()
为了方便我们用sigmoid函数进行激活:
隐藏层——输出层:
![]()
![]()
这样我们就得到了输出值out(o1)和out(o2),此时这两个输出值和我们预想的输出值肯定相差甚远那么我们就要进行反向传播来修正w以此来修正输出值。
这里要用到链式法则,我们以w5为例来看隐含层---->输出层的权值更新:
w5在![]() 中出现,
中出现,![]() 在
在![]() 中出现,
中出现,![]() 在Error中出现,由链式法则得到:
在Error中出现,由链式法则得到:
sigmoid函数的性质就是![]() ,有兴趣的同学可以自己推一下,我这里就不赘述了。从这个性质可以得到:
,有兴趣的同学可以自己推一下,我这里就不赘述了。从这个性质可以得到:
而上面正向推到的时候已经算出来了![]()
然后就可以对w5进行更新![]() ,其中lr是学习率。w6,w7,w8同理。
,其中lr是学习率。w6,w7,w8同理。
隐含层---->隐含层的权值更新 ,这里以w1为例:
周老师在西瓜书上也有完整的推到公式,写的很清楚也很好理解。
公式里各个变量的意义如下:
2.数值计算 - 手动计算,掌握细节
计算首先要初始化参数,这里就用老师给的图了
这里以w5为例,题里面给的0.23和-0.07就是上文提到的target。
其实算出来h和o以后后面就是套入公式直接算就可以了,w5和w1是一样的,不过w1算的数要多一点我就选w5举例了。
3.代码实现 - numpy手推 + pytorch自动
![]()
1、对比【numpy】和【pytorch】程序,总结并陈述。
numpy代码:
import numpy as np
def sigmoid(z):
a = 1 / (1 + np.exp(-z))
return a
def forward_propagate(x1, x2, y1, y2, w1, w2, w3, w4, w5, w6, w7, w8):
in_h1 = w1 * x1 + w3 * x2
out_h1 = sigmoid(in_h1)
in_h2 = w2 * x1 + w4 * x2
out_h2 = sigmoid(in_h2)
in_o1 = w5 * out_h1 + w7 * out_h2
out_o1 = sigmoid(in_o1)
in_o2 = w6 * out_h1 + w8 * out_h2
out_o2 = sigmoid(in_o2)
print("正向计算:o1 ,o2")
print(round(out_o1, 5), round(out_o2, 5))
error = (1 / 2) * (out_o1 - y1) ** 2 + (1 / 2) * (out_o2 - y2) ** 2
print("损失函数:均方误差")
print(round(error, 5))
return out_o1, out_o2, out_h1, out_h2
def back_propagate(out_o1, out_o2, out_h1, out_h2):
# 反向传播
d_o1 = out_o1 - y1
d_o2 = out_o2 - y2
# print(round(d_o1, 2), round(d_o2, 2))
d_w5 = d_o1 * out_o1 * (1 - out_o1) * out_h1
d_w7 = d_o1 * out_o1 * (1 - out_o1) * out_h2
# print(round(d_w5, 2), round(d_w7, 2))
d_w6 = d_o2 * out_o2 * (1 - out_o2) * out_h1
d_w8 = d_o2 * out_o2 * (1 - out_o2) * out_h2
# print(round(d_w6, 2), round(d_w8, 2))
d_w1 = (d_w5 + d_w6) * out_h1 * (1 - out_h1) * x1
d_w3 = (d_w5 + d_w6) * out_h1 * (1 - out_h1) * x2
# print(round(d_w1, 2), round(d_w3, 2))
d_w2 = (d_w7 + d_w8) * out_h2 * (1 - out_h2) * x1
d_w4 = (d_w7 + d_w8) * out_h2 * (1 - out_h2) * x2
# print(round(d_w2, 2), round(d_w4, 2))
print("反向传播:误差传给每个权值")
print(round(d_w1, 5), round(d_w2, 5), round(d_w3, 5), round(d_w4, 5), round(d_w5, 5), round(d_w6, 5),
round(d_w7, 5), round(d_w8, 5))
return d_w1, d_w2, d_w3, d_w4, d_w5, d_w6, d_w7, d_w8
def update_w(w1, w2, w3, w4, w5, w6, w7, w8):
# 步长
step = 5
w1 = w1 - step * d_w1
w2 = w2 - step * d_w2
w3 = w3 - step * d_w3
w4 = w4 - step * d_w4
w5 = w5 - step * d_w5
w6 = w6 - step * d_w6
w7 = w7 - step * d_w7
w8 = w8 - step * d_w8
return w1, w2, w3, w4, w5, w6, w7, w8
if __name__ == "__main__":
w1, w2, w3, w4, w5, w6, w7, w8 = 0.2, -0.4, 0.5, 0.6, 0.1, -0.5, -0.3, 0.8
x1, x2 = 0.5, 0.3
y1, y2 = 0.23, -0.07
print("=====输入值:x1, x2;真实输出值:y1, y2=====")
print(x1, x2, y1, y2)
print("=====更新前的权值=====")
print(round(w1, 2), round(w2, 2), round(w3, 2), round(w4, 2), round(w5, 2), round(w6, 2), round(w7, 2),
round(w8, 2))
for i in range(1000):
print("=====第" + str(i) + "轮=====")
out_o1, out_o2, out_h1, out_h2 = forward_propagate(x1, x2, y1, y2, w1, w2, w3, w4, w5, w6, w7, w8)
d_w1, d_w2, d_w3, d_w4, d_w5, d_w6, d_w7, d_w8 = back_propagate(out_o1, out_o2, out_h1, out_h2)
w1, w2, w3, w4, w5, w6, w7, w8 = update_w(w1, w2, w3, w4, w5, w6, w7, w8)
print("更新后的权值")
print(round(w1, 2), round(w2, 2), round(w3, 2), round(w4, 2), round(w5, 2), round(w6, 2), round(w7, 2),
round(w8, 2))pytorch代码:
import torch
x1, x2 = torch.Tensor([0.5]), torch.Tensor([0.3])
y1, y2 = torch.Tensor([0.23]), torch.Tensor([-0.07])
print("=====输入值:x1, x2;真实输出值:y1, y2=====")
print(x1, x2, y1, y2)
w1, w2, w3, w4, w5, w6, w7, w8 = torch.Tensor([0.2]), torch.Tensor([-0.4]), torch.Tensor([0.5]), torch.Tensor(
[0.6]), torch.Tensor([0.1]), torch.Tensor([-0.5]), torch.Tensor([-0.3]), torch.Tensor([0.8]) # 权重初始值
w1.requires_grad = True
w2.requires_grad = True
w3.requires_grad = True
w4.requires_grad = True
w5.requires_grad = True
w6.requires_grad = True
w7.requires_grad = True
w8.requires_grad = True
def sigmoid(z):
a = 1 / (1 + torch.exp(-z))
return a
def forward_propagate(x1, x2):
in_h1 = w1 * x1 + w3 * x2
out_h1 = sigmoid(in_h1) # out_h1 = torch.sigmoid(in_h1)
in_h2 = w2 * x1 + w4 * x2
out_h2 = sigmoid(in_h2) # out_h2 = torch.sigmoid(in_h2)
in_o1 = w5 * out_h1 + w7 * out_h2
out_o1 = sigmoid(in_o1) # out_o1 = torch.sigmoid(in_o1)
in_o2 = w6 * out_h1 + w8 * out_h2
out_o2 = sigmoid(in_o2) # out_o2 = torch.sigmoid(in_o2)
print("正向计算:o1 ,o2")
print(out_o1.data, out_o2.data)
return out_o1, out_o2
def loss_fuction(x1, x2, y1, y2): # 损失函数
y1_pred, y2_pred = forward_propagate(x1, x2) # 前向传播
loss = (1 / 2) * (y1_pred - y1) ** 2 + (1 / 2) * (y2_pred - y2) ** 2 # 考虑 : t.nn.MSELoss()
print("损失函数(均方误差):", loss.item())
return loss
def update_w(w1, w2, w3, w4, w5, w6, w7, w8):
# 步长
step = 1
w1.data = w1.data - step * w1.grad.data
w2.data = w2.data - step * w2.grad.data
w3.data = w3.data - step * w3.grad.data
w4.data = w4.data - step * w4.grad.data
w5.data = w5.data - step * w5.grad.data
w6.data = w6.data - step * w6.grad.data
w7.data = w7.data - step * w7.grad.data
w8.data = w8.data - step * w8.grad.data
w1.grad.data.zero_() # 注意:将w中所有梯度清零
w2.grad.data.zero_()
w3.grad.data.zero_()
w4.grad.data.zero_()
w5.grad.data.zero_()
w6.grad.data.zero_()
w7.grad.data.zero_()
w8.grad.data.zero_()
return w1, w2, w3, w4, w5, w6, w7, w8
if __name__ == "__main__":
print("=====更新前的权值=====")
print(w1.data, w2.data, w3.data, w4.data, w5.data, w6.data, w7.data, w8.data)
for i in range(1000):
print("=====第" + str(i) + "轮=====")
L = loss_fuction(x1, x2, y1, y2) # 前向传播,求 Loss,构建计算图
L.backward() # 自动求梯度,不需要人工编程实现。反向传播,求出计算图中所有梯度存入w中
print("\tgrad W: ", round(w1.grad.item(), 2), round(w2.grad.item(), 2), round(w3.grad.item(), 2),
round(w4.grad.item(), 2), round(w5.grad.item(), 2), round(w6.grad.item(), 2), round(w7.grad.item(), 2),
round(w8.grad.item(), 2))
w1, w2, w3, w4, w5, w6, w7, w8 = update_w(w1, w2, w3, w4, w5, w6, w7, w8)
print("更新后的权值")
print(w1.data, w2.data, w3.data, w4.data, w5.data, w6.data, w7.data, w8.data)numpy代码的运行结果:
pytorch代码的运行结果:
都经过1000轮训练后发现损失是差不多的,但是最后更新后的权值不一样。
2、激活函数Sigmoid用PyTorch自带函数torch.sigmoid(),观察、总结并陈述。
把torch的sigmoid换成torch.sigmoid()后的代码:
import torch
x = [0.5, 0.3] # x0, x1 = 0.5, 0.3
y = [0.23, -0.07] # y0, y1 = 0.23, -0.07
print("输入值 x0, x1:", x[0], x[1])
print("输出值 y0, y1:", y[0], y[1])
w = [torch.Tensor([0.2]), torch.Tensor([-0.4]), torch.Tensor([0.5]), torch.Tensor(
[0.6]), torch.Tensor([0.1]), torch.Tensor([-0.5]), torch.Tensor([-0.3]), torch.Tensor([0.8])] # 权重初始值
for i in range(0, 8):
w[i].requires_grad = True
print("权值w0-w7:")
for i in range(0, 8):
print(w[i].data, end=" ")
def forward_propagate(x): # 计算图
in_h1 = w[0] * x[0] + w[2] * x[1]
out_h1 = torch.sigmoid(in_h1)
in_h2 = w[1] * x[0] + w[3] * x[1]
out_h2 = torch.sigmoid(in_h2)
in_o1 = w[4] * out_h1 + w[6] * out_h2
out_o1 = torch.sigmoid(in_o1)
in_o2 = w[5] * out_h1 + w[7] * out_h2
out_o2 = torch.sigmoid(in_o2)
print("正向计算,隐藏层h1 ,h2:", end="")
print(out_h1.data, out_h2.data)
print("正向计算,预测值o1 ,o2:", end="")
print(out_o1.data, out_o2.data)
return out_o1, out_o2
def loss(x, y): # 损失函数
y_pre = forward_propagate(x) # 前向传播
loss_mse = (1 / 2) * (y_pre[0] - y[0]) ** 2 + (1 / 2) * (y_pre[1] - y[1]) ** 2 # 考虑 : t.nn.MSELoss()
print("损失函数(均方误差):", loss_mse.item())
return loss_mse
if __name__ == "__main__":
for k in range(1000):
print("\n=====第" + str(k+1) + "轮=====")
l = loss(x, y) # 前向传播,求 Loss,构建计算图
l.backward() # 反向传播,求出计算图中所有梯度存入w中. 自动求梯度,不需要人工编程实现。
print("w的梯度: ", end=" ")
for i in range(0, 8):
print(round(w[i].grad.item(), 2), end=" ") # 查看梯度
step = 1 # 步长
for i in range(0, 8):
w[i].data = w[i].data - step * w[i].grad.data # 更新权值
w[i].grad.data.zero_() # 注意:将w中所有梯度清零
print("\n更新后的权值w:")
for i in range(0, 8):
print(w[i].data, end=" ")
发现torch.sigmoid和自己手写的sigmoid得到的结果是一样的
3、激活函数Sigmoid改变为Relu,观察、总结并陈述。
import torch
x = [0.5, 0.3] # x0, x1 = 0.5, 0.3
y = [0.23, -0.07] # y0, y1 = 0.23, -0.07
print("输入值 x0, x1:", x[0], x[1])
print("输出值 y0, y1:", y[0], y[1])
w = [torch.Tensor([0.2]), torch.Tensor([-0.4]), torch.Tensor([0.5]), torch.Tensor(
[0.6]), torch.Tensor([0.1]), torch.Tensor([-0.5]), torch.Tensor([-0.3]), torch.Tensor([0.8])] # 权重初始值
for i in range(0, 8):
w[i].requires_grad = True
print("权值w0-w7:")
for i in range(0, 8):
print(w[i].data, end=" ")
def forward_propagate(x): # 计算图
in_h1 = w[0] * x[0] + w[2] * x[1]
out_h1 = torch.relu(in_h1)
in_h2 = w[1] * x[0] + w[3] * x[1]
out_h2 = torch.relu(in_h2)
in_o1 = w[4] * out_h1 + w[6] * out_h2
out_o1 = torch.relu(in_o1)
in_o2 = w[5] * out_h1 + w[7] * out_h2
out_o2 = torch.relu(in_o2)
print("正向计算,隐藏层h1 ,h2:", end="")
print(out_h1.data, out_h2.data)
print("正向计算,预测值o1 ,o2:", end="")
print(out_o1.data, out_o2.data)
return out_o1, out_o2
def loss(x, y): # 损失函数
y_pre = forward_propagate(x) # 前向传播
loss_mse = (1 / 2) * (y_pre[0] - y[0]) ** 2 + (1 / 2) * (y_pre[1] - y[1]) ** 2 # 考虑 : t.nn.MSELoss()
print("损失函数(均方误差):", loss_mse.item())
return loss_mse
if __name__ == "__main__":
for k in range(50):
print("\n=====第" + str(k+1) + "轮=====")
l = loss(x, y) # 前向传播,求 Loss,构建计算图
l.backward() # 反向传播,求出计算图中所有梯度存入w中. 自动求梯度,不需要人工编程实现。
print("w的梯度: ", end=" ")
for i in range(0, 8):
print(round(w[i].grad.item(), 2), end=" ") # 查看梯度
step = 1 # 步长
for i in range(0, 8):
w[i].data = w[i].data - step * w[i].grad.data # 更新权值
w[i].grad.data.zero_() # 注意:将w中所有梯度清零
print("\n更新后的权值w:")
for i in range(0, 8):
print(w[i].data, end=" ")
得到以下结果:
=====第1轮=====
正向计算,隐藏层h1 ,h2:tensor([0.2500]) tensor([0.])
正向计算,预测值o1 ,o2:tensor([0.0250]) tensor([0.])
损失函数(均方误差): 0.023462500423192978
w的梯度: -0.01 0.0 -0.01 0.0 -0.05 0.0 -0.0 0.0
更新后的权值w:
tensor([0.2103]) tensor([-0.4000]) tensor([0.5062]) tensor([0.6000]) tensor([0.1513]) tensor([-0.5000]) tensor([-0.3000]) tensor([0.8000])
=====第2轮=====
正向计算,隐藏层h1 ,h2:tensor([0.2570]) tensor([0.])
正向计算,预测值o1 ,o2:tensor([0.0389]) tensor([0.])
损失函数(均方误差): 0.020715968683362007
w的梯度: -0.01 0.0 -0.01 0.0 -0.05 0.0 0.0 0.0
更新后的权值w:
tensor([0.2247]) tensor([-0.4000]) tensor([0.5148]) tensor([0.6000]) tensor([0.2004]) tensor([-0.5000]) tensor([-0.3000]) tensor([0.8000])
=====第3轮=====
正向计算,隐藏层h1 ,h2:tensor([0.2668]) tensor([0.])
正向计算,预测值o1 ,o2:tensor([0.0535]) tensor([0.])
损失函数(均方误差): 0.01803365722298622
w的梯度: -0.02 0.0 -0.01 0.0 -0.05 0.0 0.0 0.0
更新后的权值w:
tensor([0.2424]) tensor([-0.4000]) tensor([0.5254]) tensor([0.6000]) tensor([0.2475]) tensor([-0.5000]) tensor([-0.3000]) tensor([0.8000])
=====第4轮=====
正向计算,隐藏层h1 ,h2:tensor([0.2788]) tensor([0.])
正向计算,预测值o1 ,o2:tensor([0.0690]) tensor([0.])
损失函数(均方误差): 0.015410471707582474
w的梯度: -0.02 0.0 -0.01 0.0 -0.04 0.0 0.0 0.0
更新后的权值w:
tensor([0.2623]) tensor([-0.4000]) tensor([0.5374]) tensor([0.6000]) tensor([0.2924]) tensor([-0.5000]) tensor([-0.3000]) tensor([0.8000])
=====第5轮=====
正向计算,隐藏层h1 ,h2:tensor([0.2924]) tensor([0.])
正向计算,预测值o1 ,o2:tensor([0.0855]) tensor([0.])
损失函数(均方误差): 0.012893404811620712
w的梯度: -0.02 0.0 -0.01 0.0 -0.04 0.0 0.0 0.0
更新后的权值w:
tensor([0.2834]) tensor([-0.4000]) tensor([0.5501]) tensor([0.6000]) tensor([0.3346]) tensor([-0.5000]) tensor([-0.3000]) tensor([0.8000])
对比一下torch的损失函数
=====第1轮=====
正向计算,隐藏层h1 ,h2:tensor([0.5622]) tensor([0.4950])
正向计算,预测值o1 ,o2:tensor([0.4769]) tensor([0.5287])
损失函数(均方误差): 0.2097097933292389
w的梯度: -0.01 0.01 -0.01 0.01 0.03 0.08 0.03 0.07
更新后的权值w:
tensor([0.2084]) tensor([-0.4126]) tensor([0.5051]) tensor([0.5924]) tensor([0.0654]) tensor([-0.5839]) tensor([-0.3305]) tensor([0.7262])
=====第2轮=====
正向计算,隐藏层h1 ,h2:tensor([0.5636]) tensor([0.4929])
正向计算,预测值o1 ,o2:tensor([0.4685]) tensor([0.5072])
损失函数(均方误差): 0.19503259658813477
w的梯度: -0.01 0.01 -0.01 0.01 0.03 0.08 0.03 0.07
更新后的权值w:
tensor([0.2183]) tensor([-0.4232]) tensor([0.5110]) tensor([0.5861]) tensor([0.0319]) tensor([-0.6652]) tensor([-0.3598]) tensor([0.6550])
=====第3轮=====
正向计算,隐藏层h1 ,h2:tensor([0.5652]) tensor([0.4910])
正向计算,预测值o1 ,o2:tensor([0.4604]) tensor([0.4864])
损失函数(均方误差): 0.1813509315252304
w的梯度: -0.01 0.01 -0.01 0.01 0.03 0.08 0.03 0.07
更新后的权值w:
tensor([0.2294]) tensor([-0.4321]) tensor([0.5177]) tensor([0.5808]) tensor([-0.0005]) tensor([-0.7437]) tensor([-0.3879]) tensor([0.5868])
=====第4轮=====
正向计算,隐藏层h1 ,h2:tensor([0.5671]) tensor([0.4896])
正向计算,预测值o1 ,o2:tensor([0.4526]) tensor([0.4664])
损失函数(均方误差): 0.16865134239196777
w的梯度: -0.01 0.01 -0.01 0.0 0.03 0.08 0.03 0.07
更新后的权值w:
tensor([0.2416]) tensor([-0.4392]) tensor([0.5250]) tensor([0.5765]) tensor([-0.0317]) tensor([-0.8195]) tensor([-0.4149]) tensor([0.5214])
=====第5轮=====
正向计算,隐藏层h1 ,h2:tensor([0.5691]) tensor([0.4883])
正向计算,预测值o1 ,o2:tensor([0.4451]) tensor([0.4473])
损失函数(均方误差): 0.15690487623214722
w的梯度: -0.01 0.01 -0.01 0.0 0.03 0.07 0.03 0.06
更新后的权值w:
tensor([0.2547]) tensor([-0.4447]) tensor([0.5328]) tensor([0.5732]) tensor([-0.0620]) tensor([-0.8922]) tensor([-0.4408]) tensor([0.4590])从结果中可以看到relu损失函数下降的非常快到15轮左右就达到了最低而最后的更新出来的权值跟numpy和torch的都不一样
更新后的权值w:
tensor([0.4287]) tensor([-0.4000]) tensor([0.6372]) tensor([0.6000]) tensor([0.5672]) tensor([-0.5000]) tensor([-0.3000]) tensor([0.8000]) 小结一下ReLU函数相对于tanh和sigmoid函数好在哪里:
第一,采用sigmoid等函数,算激活函数是(指数运算),计算量大;反向传播求误差梯度时,求导涉及除法,计算量相对大。而采用Relu激活函数,整个过程的计算量节省很多。
第二,对于深层网络,sigmoid函数反向传播时,很容易就会出现梯度消失的情况(在sigmoid接近饱和区时,变换太缓慢,导数趋于0),这种情况会造成信息丢失,梯度消失在网络层数多的时候尤其明显,从而无法完成深层网络的训练。
第三,ReLU会使一部分神经元的输出为0,这样就造成了网络的稀疏性,并且减少了参数的相互依存关系,缓解了过拟合问题的发生。
关于relu和sigmoid的区别可以参考:http://t.csdn.cn/9uIQD
4、损失函数MSE用PyTorch自带函数 t.nn.MSELoss()替代,观察、总结并陈述。
# https://blog.csdn.net/qq_41033011/article/details/109325070
# https://github.com/Darwlr/Deep_learning/blob/master/06%20Pytorch%E5%AE%9E%E7%8E%B0%E5%8F%8D%E5%90%91%E4%BC%A0%E6%92%AD.ipynb
# torch.nn.Sigmoid(h_in)
import torch
x1, x2 = torch.Tensor([0.5]), torch.Tensor([0.3])
y1, y2 = torch.Tensor([0.23]), torch.Tensor([-0.07])
print("=====输入值:x1, x2;真实输出值:y1, y2=====")
print(x1, x2, y1, y2)
w1, w2, w3, w4, w5, w6, w7, w8 = torch.Tensor([0.2]), torch.Tensor([-0.4]), torch.Tensor([0.5]), torch.Tensor(
[0.6]), torch.Tensor([0.1]), torch.Tensor([-0.5]), torch.Tensor([-0.3]), torch.Tensor([0.8]) # 权重初始值
w1.requires_grad = True
w2.requires_grad = True
w3.requires_grad = True
w4.requires_grad = True
w5.requires_grad = True
w6.requires_grad = True
w7.requires_grad = True
w8.requires_grad = True
def sigmoid(z):
a = 1 / (1 + torch.exp(-z))
return a
def forward_propagate(x1, x2):
in_h1 = w1 * x1 + w3 * x2
out_h1 = sigmoid(in_h1) # out_h1 = torch.sigmoid(in_h1)
in_h2 = w2 * x1 + w4 * x2
out_h2 = sigmoid(in_h2) # out_h2 = torch.sigmoid(in_h2)
in_o1 = w5 * out_h1 + w7 * out_h2
out_o1 = sigmoid(in_o1) # out_o1 = torch.sigmoid(in_o1)
in_o2 = w6 * out_h1 + w8 * out_h2
out_o2 = sigmoid(in_o2) # out_o2 = torch.sigmoid(in_o2)
print("正向计算:o1 ,o2")
print(out_o1.data, out_o2.data)
return out_o1, out_o2
def loss_fuction(x1, x2, y1, y2): # 损失函数
y1_pred, y2_pred = forward_propagate(x1, x2) # 前向传播
mse = torch.nn.MSELoss()
loss =mse(y1_pred,y1) + mse(y2_pred,y2) # 考虑 : t.nn.MSELoss()
print("损失函数(均方误差):", loss.item())
return loss
def update_w(w1, w2, w3, w4, w5, w6, w7, w8):
# 步长
step = 1
w1.data = w1.data - step * w1.grad.data
w2.data = w2.data - step * w2.grad.data
w3.data = w3.data - step * w3.grad.data
w4.data = w4.data - step * w4.grad.data
w5.data = w5.data - step * w5.grad.data
w6.data = w6.data - step * w6.grad.data
w7.data = w7.data - step * w7.grad.data
w8.data = w8.data - step * w8.grad.data
w1.grad.data.zero_() # 注意:将w中所有梯度清零
w2.grad.data.zero_()
w3.grad.data.zero_()
w4.grad.data.zero_()
w5.grad.data.zero_()
w6.grad.data.zero_()
w7.grad.data.zero_()
w8.grad.data.zero_()
return w1, w2, w3, w4, w5, w6, w7, w8
if __name__ == "__main__":
print("=====更新前的权值=====")
print(w1.data, w2.data, w3.data, w4.data, w5.data, w6.data, w7.data, w8.data)
for i in range(1000):
print("=====第" + str(i) + "轮=====")
L = loss_fuction(x1, x2, y1, y2) # 前向传播,求 Loss,构建计算图
L.backward() # 自动求梯度,不需要人工编程实现。反向传播,求出计算图中所有梯度存入w中
print("\tgrad W: ", round(w1.grad.item(), 2), round(w2.grad.item(), 2), round(w3.grad.item(), 2),
round(w4.grad.item(), 2), round(w5.grad.item(), 2), round(w6.grad.item(), 2), round(w7.grad.item(), 2),
round(w8.grad.item(), 2))
w1, w2, w3, w4, w5, w6, w7, w8 = update_w(w1, w2, w3, w4, w5, w6, w7, w8)
print("更新后的权值")
print(w1.data, w2.data, w3.data, w4.data, w5.data, w6.data, w7.data, w8.data)得到更新后的权重:
=====第999轮=====
正向计算:o1 ,o2
tensor([0.2298]) tensor([0.0050])
损失函数(均方误差): 0.005628134589642286
grad W: -0.0 -0.0 -0.0 -0.0 -0.0 0.0 -0.0 0.0
更新后的权值
tensor([1.8441]) tensor([0.3147]) tensor([1.4865]) tensor([1.0288]) tensor([-0.7469]) tensor([-4.6932]) tensor([-0.9992]) tensor([-2.5217])
发现损失函数变大了不少,说明还是手写的mse好一点
5、损失函数MSE改变为交叉熵,观察、总结并陈述。
# https://blog.csdn.net/qq_41033011/article/details/109325070
# https://github.com/Darwlr/Deep_learning/blob/master/06%20Pytorch%E5%AE%9E%E7%8E%B0%E5%8F%8D%E5%90%91%E4%BC%A0%E6%92%AD.ipynb
# torch.nn.Sigmoid(h_in)
import torch
x1, x2 = torch.Tensor([0.5]), torch.Tensor([0.3])
y1, y2 = torch.Tensor([0.23]), torch.Tensor([-0.07])
print("=====输入值:x1, x2;真实输出值:y1, y2=====")
print(x1, x2, y1, y2)
w1, w2, w3, w4, w5, w6, w7, w8 = torch.Tensor([0.2]), torch.Tensor([-0.4]), torch.Tensor([0.5]), torch.Tensor(
[0.6]), torch.Tensor([0.1]), torch.Tensor([-0.5]), torch.Tensor([-0.3]), torch.Tensor([0.8]) # 权重初始值
w1.requires_grad = True
w2.requires_grad = True
w3.requires_grad = True
w4.requires_grad = True
w5.requires_grad = True
w6.requires_grad = True
w7.requires_grad = True
w8.requires_grad = True
def sigmoid(z):
a = 1 / (1 + torch.exp(-z))
return a
def forward_propagate(x1, x2):
in_h1 = w1 * x1 + w3 * x2
out_h1 = sigmoid(in_h1) # out_h1 = torch.sigmoid(in_h1)
in_h2 = w2 * x1 + w4 * x2
out_h2 = sigmoid(in_h2) # out_h2 = torch.sigmoid(in_h2)
in_o1 = w5 * out_h1 + w7 * out_h2
out_o1 = sigmoid(in_o1) # out_o1 = torch.sigmoid(in_o1)
in_o2 = w6 * out_h1 + w8 * out_h2
out_o2 = sigmoid(in_o2) # out_o2 = torch.sigmoid(in_o2)
print("正向计算:o1 ,o2")
print(out_o1.data, out_o2.data)
return out_o1, out_o2
def loss_fuction(x1, x2, y1, y2):
y1_pred, y2_pred = forward_propagate(x1, x2)
loss_func = torch.nn.CrossEntropyLoss() # 创建交叉熵损失函数
y_pred = torch.stack([y1_pred, y2_pred], dim=1)
y = torch.stack([y1, y2], dim=1)
loss = loss_func(y_pred, y) # 计算
print("损失函数(交叉熵损失):", loss.item())
return loss
def update_w(w1, w2, w3, w4, w5, w6, w7, w8):
# 步长
step = 1
w1.data = w1.data - step * w1.grad.data
w2.data = w2.data - step * w2.grad.data
w3.data = w3.data - step * w3.grad.data
w4.data = w4.data - step * w4.grad.data
w5.data = w5.data - step * w5.grad.data
w6.data = w6.data - step * w6.grad.data
w7.data = w7.data - step * w7.grad.data
w8.data = w8.data - step * w8.grad.data
w1.grad.data.zero_() # 注意:将w中所有梯度清零
w2.grad.data.zero_()
w3.grad.data.zero_()
w4.grad.data.zero_()
w5.grad.data.zero_()
w6.grad.data.zero_()
w7.grad.data.zero_()
w8.grad.data.zero_()
return w1, w2, w3, w4, w5, w6, w7, w8
if __name__ == "__main__":
print("=====更新前的权值=====")
print(w1.data, w2.data, w3.data, w4.data, w5.data, w6.data, w7.data, w8.data)
for i in range(1000):
print("=====第" + str(i) + "轮=====")
L = loss_fuction(x1, x2, y1, y2) # 前向传播,求 Loss,构建计算图
L.backward() # 自动求梯度,不需要人工编程实现。反向传播,求出计算图中所有梯度存入w中
print("\tgrad W: ", round(w1.grad.item(), 2), round(w2.grad.item(), 2), round(w3.grad.item(), 2),
round(w4.grad.item(), 2), round(w5.grad.item(), 2), round(w6.grad.item(), 2), round(w7.grad.item(), 2),
round(w8.grad.item(), 2))
w1, w2, w3, w4, w5, w6, w7, w8 = update_w(w1, w2, w3, w4, w5, w6, w7, w8)
print("更新后的权值")
print(w1.data, w2.data, w3.data, w4.data, w5.data, w6.data, w7.data, w8.data)得到更新后的权重
=====第999轮=====
正向计算:o1 ,o2
tensor([0.9929]) tensor([0.0072])
损失函数(交叉熵损失): -0.018253758549690247
grad W: -0.0 -0.0 -0.0 -0.0 -0.0 0.0 -0.0 0.0
更新后的权值
tensor([2.2809]) tensor([0.6580]) tensor([1.7485]) tensor([1.2348]) tensor([3.8104]) tensor([-4.2013]) tensor([2.5933]) tensor([-2.0866])需要注意的是,需要将输入通过Logsoftmax函数得到输出概率后再进行负对数似然损失函数计算。
6、改变步长,训练次数,观察、总结并陈述。
步长是1的时候训练次数变成10:
=====第9轮=====
正向计算:o1 ,o2
tensor([0.4109]) tensor([0.3647])
损失函数(均方误差): 0.11082295328378677
grad W: -0.02 0.0 -0.01 0.0 0.03 0.06 0.02 0.05
更新后的权值
tensor([0.3273]) tensor([-0.4547]) tensor([0.5764]) tensor([0.5672]) tensor([-0.1985]) tensor([-1.2127]) tensor([-0.5561]) tensor([0.1883])发现损失还是比较大的,训练次数变100:
=====第99轮=====
正向计算:o1 ,o2
tensor([0.2378]) tensor([0.0736])
损失函数(均方误差): 0.010342842899262905
grad W: -0.0 -0.0 -0.0 -0.0 0.0 0.01 0.0 0.01
更新后的权值
tensor([0.9865]) tensor([-0.2037]) tensor([0.9719]) tensor([0.7178]) tensor([-0.8628]) tensor([-2.8459]) tensor([-1.0866]) tensor([-1.1112])
发现训练100次后损失还是没有到最小,把训练次数变成150:
=====第148轮=====
正向计算:o1 ,o2
tensor([0.2297]) tensor([0.0528])
损失函数(均方误差): 0.0075379335321486
grad W: -0.0 -0.0 -0.0 -0.0 -0.0 0.0 -0.0 0.0
=====第149轮=====
正向计算:o1 ,o2
tensor([0.2296]) tensor([0.0525])
损失函数(均方误差): 0.007501816377043724
grad W: -0.0 -0.0 -0.0 -0.0 -0.0 0.0 -0.0 0.0
更新后的权值
tensor([1.1088]) tensor([-0.1431]) tensor([1.0453]) tensor([0.7541]) tensor([-0.8789]) tensor([-3.1110]) tensor([-1.0990]) tensor([-1.3145])
进程已结束,退出代码为 0
发现到150后就已经达到最小的损失了。
我们把step变成2后训练10次:
=====第9轮=====
正向计算:o1 ,o2
tensor([0.3609]) tensor([0.2613])
损失函数(均方误差): 0.06343768537044525
grad W: -0.01 -0.0 -0.01 -0.0 0.02 0.04 0.01 0.03
更新后的权值
tensor([0.4696]) tensor([-0.4351]) tensor([0.6618]) tensor([0.5790]) tensor([-0.4145]) tensor([-1.6882]) tensor([-0.7343]) tensor([-0.2040])发现步长变为2后损失下降变快了。我们再把训练次数变为50
=====第49轮=====
正向计算:o1 ,o2
tensor([0.2376]) tensor([0.0736])
损失函数(均方误差): 0.01034099142998457
grad W: -0.0 -0.0 -0.0 -0.0 0.0 0.01 0.0 0.01
更新后的权值
tensor([0.9834]) tensor([-0.2099]) tensor([0.9701]) tensor([0.7141]) tensor([-0.8661]) tensor([-2.8555]) tensor([-1.0899]) tensor([-1.1204])发现step=2时训练50次就已经达到了step=1时训练100次的效果。我们再改变训练次数100次:
=====第98轮=====
正向计算:o1 ,o2
tensor([0.2281]) tensor([0.0415])
损失函数(均方误差): 0.006220802664756775
grad W: -0.0 -0.0 -0.0 -0.0 -0.0 0.0 -0.0 0.0
=====第99轮=====
正向计算:o1 ,o2
tensor([0.2280]) tensor([0.0412])
损失函数(均方误差): 0.006181709934026003
grad W: -0.0 -0.0 -0.0 -0.0 -0.0 0.0 -0.0 0.0
更新后的权值
tensor([1.1885]) tensor([-0.1073]) tensor([1.0931]) tensor([0.7756]) tensor([-0.8715]) tensor([-3.3002]) tensor([-1.0941]) tensor([-1.4604])
进程已结束,退出代码为 0
发现损失已经到最低,并且损失比step=1时小了一点。
再改变step=5时,训练10次:
=====第9轮=====
正向计算:o1 ,o2
tensor([0.2777]) tensor([0.1328])
损失函数(均方误差): 0.021693594753742218
grad W: -0.01 -0.0 -0.0 -0.0 0.01 0.02 0.0 0.01
更新后的权值
tensor([0.7494]) tensor([-0.3390]) tensor([0.8297]) tensor([0.6366]) tensor([-0.7496]) tensor([-2.4153]) tensor([-1.0027]) tensor([-0.7872])发现这次损失下降的更快了,训练次数变成50:
=====第48轮=====
正向计算:o1 ,o2
tensor([0.2280]) tensor([0.0346])
损失函数(均方误差): 0.005469010677188635
grad W: -0.0 -0.0 -0.0 -0.0 -0.0 0.0 -0.0 0.0
=====第49轮=====
正向计算:o1 ,o2
tensor([0.2280]) tensor([0.0340])
损失函数(均方误差): 0.00540730869397521
grad W: -0.0 -0.0 -0.0 -0.0 -0.0 0.0 -0.0 0.0
更新后的权值
tensor([1.2391]) tensor([-0.0953]) tensor([1.1234]) tensor([0.7828]) tensor([-0.8628]) tensor([-3.4584]) tensor([-1.0903]) tensor([-1.5854])
进程已结束,退出代码为 0
发现损失已经到最低并且损失比step=1、2时都低。
但是如果step过大,我在这里把step调为200
=====第0轮=====
正向计算:o1 ,o2
tensor([0.4769]) tensor([0.5287])
损失函数(均方误差): 0.2097097933292389
grad W: -0.01 0.01 -0.01 0.01 0.03 0.08 0.03 0.07
=====第1轮=====
正向计算:o1 ,o2
tensor([0.0016]) tensor([1.1962e-07])
损失函数(均方误差): 0.02853141352534294
grad W: 0.0 0.0 0.0 0.0 -0.0 0.0 -0.0 0.0这就可以发现步长太大了,损失已经比原来大很多了。
7、权值w1-w8初始值换为随机数,对比“指定权值”的结果,观察、总结并陈述。
import torch
x1, x2 = torch.Tensor([0.5]), torch.Tensor([0.3])
y1, y2 = torch.Tensor([0.23]), torch.Tensor([-0.07])
print("=====输入值:x1, x2;真实输出值:y1, y2=====")
print(x1, x2, y1, y2)
w1, w2, w3, w4, w5, w6, w7, w8 = torch.randn(1, 1), torch.randn(1, 1), torch.randn(1, 1), torch.randn(1, 1), torch.randn(1, 1), torch.randn(1, 1), torch.randn(1, 1), torch.randn(1, 1) #权重初始值
w1.requires_grad = True
w2.requires_grad = True
w3.requires_grad = True
w4.requires_grad = True
w5.requires_grad = True
w6.requires_grad = True
w7.requires_grad = True
w8.requires_grad = True
def sigmoid(z):
a = 1 / (1 + torch.exp(-z))
return a
def forward_propagate(x1, x2):
in_h1 = w1 * x1 + w3 * x2
out_h1 = sigmoid(in_h1) # out_h1 = torch.sigmoid(in_h1)
in_h2 = w2 * x1 + w4 * x2
out_h2 = sigmoid(in_h2) # out_h2 = torch.sigmoid(in_h2)
in_o1 = w5 * out_h1 + w7 * out_h2
out_o1 = sigmoid(in_o1) # out_o1 = torch.sigmoid(in_o1)
in_o2 = w6 * out_h1 + w8 * out_h2
out_o2 = sigmoid(in_o2) # out_o2 = torch.sigmoid(in_o2)
print("正向计算:o1 ,o2")
print(out_o1.data, out_o2.data)
return out_o1, out_o2
def loss_fuction(x1, x2, y1, y2): # 损失函数
y1_pred, y2_pred = forward_propagate(x1, x2) # 前向传播
loss = (1 / 2) * (y1_pred - y1) ** 2 + (1 / 2) * (y2_pred - y2) ** 2 # 考虑 : t.nn.MSELoss()
print("损失函数(均方误差):", loss.item())
return loss
def update_w(w1, w2, w3, w4, w5, w6, w7, w8):
# 步长
step = 1
w1.data = w1.data - step * w1.grad.data
w2.data = w2.data - step * w2.grad.data
w3.data = w3.data - step * w3.grad.data
w4.data = w4.data - step * w4.grad.data
w5.data = w5.data - step * w5.grad.data
w6.data = w6.data - step * w6.grad.data
w7.data = w7.data - step * w7.grad.data
w8.data = w8.data - step * w8.grad.data
w1.grad.data.zero_() # 注意:将w中所有梯度清零
w2.grad.data.zero_()
w3.grad.data.zero_()
w4.grad.data.zero_()
w5.grad.data.zero_()
w6.grad.data.zero_()
w7.grad.data.zero_()
w8.grad.data.zero_()
return w1, w2, w3, w4, w5, w6, w7, w8
if __name__ == "__main__":
print("=====更新前的权值=====")
print(w1.data, w2.data, w3.data, w4.data, w5.data, w6.data, w7.data, w8.data)
for i in range(50):
print("=====第" + str(i) + "轮=====")
L = loss_fuction(x1, x2, y1, y2) # 前向传播,求 Loss,构建计算图
L.backward() # 自动求梯度,不需要人工编程实现。反向传播,求出计算图中所有梯度存入w中
print("\tgrad W: ", round(w1.grad.item(), 2), round(w2.grad.item(), 2), round(w3.grad.item(), 2),
round(w4.grad.item(), 2), round(w5.grad.item(), 2), round(w6.grad.item(), 2), round(w7.grad.item(), 2),
round(w8.grad.item(), 2))
w1, w2, w3, w4, w5, w6, w7, w8 = update_w(w1, w2, w3, w4, w5, w6, w7, w8)
print("更新后的权值")
print(w1.data, w2.data, w3.data, w4.data, w5.data, w6.data, w7.data, w8.data)得到以下结果:
=====第0轮=====
正向计算:o1 ,o2
tensor([[0.4912]]) tensor([[0.4686]])
损失函数(均方误差): 0.1791301667690277
grad W: -0.0 -0.0 -0.0 -0.0 0.03 0.06 0.04 0.07=====第60轮=====
正向计算:o1 ,o2
tensor([[0.2681]]) tensor([[0.1164]])
损失函数(均方误差): 0.01809021271765232
grad W: -0.0 -0.01 -0.0 -0.0 0.0 0.01 0.0 0.01=====第999轮=====
正向计算:o1 ,o2
tensor([[0.2295]]) tensor([[0.0099]])
损失函数(均方误差): 0.0031887246295809746
grad W: -0.0 -0.0 -0.0 -0.0 -0.0 0.0 -0.0 0.0
更新后的权值
tensor([[0.2719]]) tensor([[1.1898]]) tensor([[0.9440]]) tensor([[1.6113]]) tensor([[-1.6006]]) tensor([[-2.6337]]) tensor([[-0.3288]]) tensor([[-4.0496]])
进程已结束,退出代码为 0
发现最后的结果是一样的,但是下降速度变慢了很多,所以说明最后的结果跟初始权重无关,只不过会影响下降速度。
8、权值w1-w8初始值换为0,观察、总结并陈述。
import torch
x1, x2 = torch.Tensor([0.5]), torch.Tensor([0.3])
y1, y2 = torch.Tensor([0.23]), torch.Tensor([-0.07])
print("=====输入值:x1, x2;真实输出值:y1, y2=====")
print(x1, x2, y1, y2)
w1, w2, w3, w4, w5, w6, w7, w8 = torch.Tensor([0]), torch.Tensor([0]), torch.Tensor([0]), torch.Tensor(
[0]), torch.Tensor([0]), torch.Tensor([0]), torch.Tensor([0]), torch.Tensor([0]) # 权重初始值
w1.requires_grad = True
w2.requires_grad = True
w3.requires_grad = True
w4.requires_grad = True
w5.requires_grad = True
w6.requires_grad = True
w7.requires_grad = True
w8.requires_grad = True
def sigmoid(z):
a = 1 / (1 + torch.exp(-z))
return a
def forward_propagate(x1, x2):
in_h1 = w1 * x1 + w3 * x2
out_h1 = sigmoid(in_h1) # out_h1 = torch.sigmoid(in_h1)
in_h2 = w2 * x1 + w4 * x2
out_h2 = sigmoid(in_h2) # out_h2 = torch.sigmoid(in_h2)
in_o1 = w5 * out_h1 + w7 * out_h2
out_o1 = sigmoid(in_o1) # out_o1 = torch.sigmoid(in_o1)
in_o2 = w6 * out_h1 + w8 * out_h2
out_o2 = sigmoid(in_o2) # out_o2 = torch.sigmoid(in_o2)
print("正向计算:o1 ,o2")
print(out_o1.data, out_o2.data)
return out_o1, out_o2
def loss_fuction(x1, x2, y1, y2): # 损失函数
y1_pred, y2_pred = forward_propagate(x1, x2) # 前向传播
loss = (1 / 2) * (y1_pred - y1) ** 2 + (1 / 2) * (y2_pred - y2) ** 2 # 考虑 : t.nn.MSELoss()
print("损失函数(均方误差):", loss.item())
return loss
def update_w(w1, w2, w3, w4, w5, w6, w7, w8):
# 步长
step = 1
w1.data = w1.data - step * w1.grad.data
w2.data = w2.data - step * w2.grad.data
w3.data = w3.data - step * w3.grad.data
w4.data = w4.data - step * w4.grad.data
w5.data = w5.data - step * w5.grad.data
w6.data = w6.data - step * w6.grad.data
w7.data = w7.data - step * w7.grad.data
w8.data = w8.data - step * w8.grad.data
w1.grad.data.zero_() # 注意:将w中所有梯度清零
w2.grad.data.zero_()
w3.grad.data.zero_()
w4.grad.data.zero_()
w5.grad.data.zero_()
w6.grad.data.zero_()
w7.grad.data.zero_()
w8.grad.data.zero_()
return w1, w2, w3, w4, w5, w6, w7, w8
if __name__ == "__main__":
print("=====更新前的权值=====")
print(w1.data, w2.data, w3.data, w4.data, w5.data, w6.data, w7.data, w8.data)
for i in range(1000):
print("=====第" + str(i) + "轮=====")
L = loss_fuction(x1, x2, y1, y2) # 前向传播,求 Loss,构建计算图
L.backward() # 自动求梯度,不需要人工编程实现。反向传播,求出计算图中所有梯度存入w中
print("\tgrad W: ", round(w1.grad.item(), 2), round(w2.grad.item(), 2), round(w3.grad.item(), 2),
round(w4.grad.item(), 2), round(w5.grad.item(), 2), round(w6.grad.item(), 2), round(w7.grad.item(), 2),
round(w8.grad.item(), 2))
w1, w2, w3, w4, w5, w6, w7, w8 = update_w(w1, w2, w3, w4, w5, w6, w7, w8)
print("更新后的权值")
print(w1.data, w2.data, w3.data, w4.data, w5.data, w6.data, w7.data, w8.data)得到以下结果:
=====第0轮=====
正向计算:o1 ,o2
tensor([0.5000]) tensor([0.5000])
损失函数(均方误差): 0.1988999992609024
grad W: 0.0 0.0 0.0 0.0 0.03 0.07 0.03 0.07=====第59轮=====
正向计算:o1 ,o2
tensor([0.2685]) tensor([0.1172])
损失函数(均方误差): 0.018268289044499397
grad W: -0.0 -0.0 -0.0 -0.0 0.0 0.01 0.0 0.01=====第99轮=====
正向计算:o1 ,o2
tensor([0.2391]) tensor([0.0759])
损失函数(均方误差): 0.01068986114114523
grad W: -0.0 -0.0 -0.0 -0.0 0.0 0.01 0.0 0.01=====第999轮=====
正向计算:o1 ,o2
tensor([0.2296]) tensor([0.0096])
损失函数(均方误差): 0.003165625501424074
grad W: -0.0 -0.0 -0.0 -0.0 -0.0 0.0 -0.0 0.0
更新后的权值
tensor([1.1809]) tensor([1.1809]) tensor([0.7085]) tensor([0.7085]) tensor([-0.8765]) tensor([-3.3598]) tensor([-0.8765]) tensor([-3.3598])发现最后的损失是一样的,只不过权值全是0后下降更慢了,也应证了上面的结论:最后的结果跟初始权重无关,只不过会影响下降速度。
9、全面总结反向传播原理和编码实现,认真写心得体会。
反向传播算法可以看成是梯度下降法在神经网络中的变形版本,它的原理主要利用了链式法则,通过递归的方式求解微分。
正向传播与反向传播其实是同时使用的。
首先,你需要正向传播,来计算z对w的偏导,进而求出sigmoid’(z)是多少。然后,根据输出层输出的数据进行反向传播,计算出l对z的偏导是多少,最后,代入到公式0当中,即可求出l对w的偏导是多少。注意,这个偏导,其实反应的就是梯度。然后我们利用梯度下降等方法,对这个w不断进行迭代(也就是权值优化的过程),使得损失函数越来越小,整体模型也越来越接近于真实值。
在这次实验中用了不同的损失函数和激活函数,还有步长和训练次数的改变,虽然原来也写过反向传播的代码,但是没有过去进行改变,只是从书上了解的一些结论,这次实验进行实践后对这些知识了解更加透彻了,并且这次的实验也查询了很多资料,在这里我整理了一些我认为反向传播写的比较好的文章分享给大家。
http://t.csdn.cn/R6c74
http://t.csdn.cn/mqmNf
http://t.csdn.cn/zSPSv










