【数据结构】基础:堆
【数据结构】基础:堆
摘要:本文主要介绍数据结构堆,分别介绍其概念、实现和应用。
文章目录
- 【数据结构】基础:堆
-
- 一、概述
-
- 1.1 概念
- 1.2 性质
- 二、实现
-
- 2.1 定义
- 2.2 初始化与销毁
- 2.3 入堆
- 2.4 出堆
- 2.5 堆的创建
- 2.6 其他
- 三、应用
-
- 3.1 堆排序
- 3.2 Top-K问题
一、概述
1.1 概念
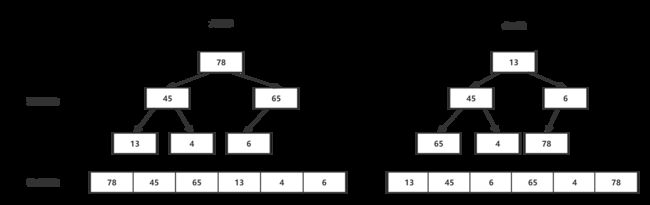
如果有一个关键码的集合K = {k0,k1, k2,…,kn-1},把它的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中,并满足:K[i] <= K[2i+1] 且 K[i]<= K[2i+2] (K[i] >= K[2i+1] 且 K[i] >= K[2i+2]) i = 0,1,2…,则称为小堆(或大堆)。将根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆。逻辑结构与物理结构图示如下:
1.2 性质
-
堆中某个节点的值总是不大于或不小于其父节点的值
小堆:所有父亲都小于或者等于孩子
大堆:所有父亲都大于或者等于孩子
-
堆总是一棵完全二叉树
-
父亲与孩子下标关系
parent_pos = (child_pos - 1) /2
rightChild_pos = parent_pos * 2 + 2
leftChild_pos = parent_pos * 2 + 1
-
左孩子下标为奇数,右孩子下标为偶数
二、实现
2.1 定义
由于栈的定义过程中,物理结构为数组,因此在此使用顺序表的形式实现,而定义的结构体,与顺序表相似
typedef int HeapDataType;
struct Heap {
HeapDataType* arr;
int size;
int capacity;
};
typedef struct Heap Heap;
2.2 初始化与销毁
初始化:对栈的每个成员进行赋初值
void HeapInit(Heap* pheap) {
assert(pheap);
pheap->arr = NULL;
pheap->capacity = pheap->size = 0;
}
销毁:由于是通过顺序表的形式呈现,因此会在栈区开辟空间,销毁即释放在栈区开辟的空间
void HeapDestory(Heap* pheap) {
assert(pheap);
free(pheap->arr);
pheap->arr = NULL;
pheap->size = pheap->capacity = 0;
}
2.3 入堆
由于堆的特殊性质,不可以随意对堆进行插入。从逻辑结构入手,可以现在末尾插入,然后不断往上移动,这样就不会影响其他子树,对堆的影响程度较小,而且每次移动进行的是交换操作,高度相较于各个节点来说是很小的,因此复杂度也会小。向上移动的方法是与父节点进行比较,如果子节点较大,就可以与父节点进行交换,并与新的子树继续比较,直到为根或者不需要当前位置合法(比父节点小)为止。当然还需要注意各种细节,有了这样的思路,可以具体书写代码流程与图示如下(以大堆为例):
- 断言判断堆是否有效
- 判断是否需要扩容
- 尾插
- 向上移动
void AjustUp(HeapDataType* arr, int child_pos) {
int parent_pos = (child_pos - 1) / 2;
while (child_pos > 0) {
if (arr[parent_pos] < arr[child_pos]) {
swap(&arr[parent_pos], &arr[child_pos]);
child_pos = parent_pos;
parent_pos = (child_pos - 1) / 2;
}
else
break;
}
}
void HeapPush(Heap* pheap, HeapDataType val) {
assert(pheap);
// 判断是否需要扩容
if (pheap->capacity == pheap->size) {
int capacityTemp = pheap->capacity == 0 ? 4 : pheap->capacity * 2;
HeapDataType* ptemp = (HeapDataType*)realloc(pheap->arr,sizeof(HeapDataType) * capacityTemp);
if (ptemp == NULL) {
perror("realloc");
exit(-1);
}
pheap->arr = ptemp;
pheap->capacity = capacityTemp;
}
// 插入到最后一个
pheap->arr[pheap->size] = val;
pheap->size++;
// 对最后一个元素上移操作
AjustUp(pheap->arr, pheap->size - 1);
}
2.4 出堆
出堆实际上是要根进行出堆,如果直接覆盖,会出现许多问题,既不符合堆的性质,也有较高的复杂度。为了减少对堆的影响,首先将堆的根与末尾进行交换,删除末尾,将新的根节点进行下移。这样复杂度与高度相关,复杂度较低。下移的思路为对找出最大子节点,如果父节点比最大子节点小,就与其进行交换,并重新确定父节点与最大子节点,持续循环下去,直到为叶节点。
void AjustDown(HeapDataType* arr, int len, int parent_pos) {
int child_pos = parent_pos * 2 + 1;
while (child_pos < len) {
if (child_pos + 1 < len && arr[child_pos + 1] > arr[child_pos]) {
child_pos = child_pos + 1;
}
if (arr[parent_pos] < arr[child_pos]) {
swap(&arr[parent_pos], &arr[child_pos]);
parent_pos = child_pos;
child_pos = parent_pos * 2 + 1;
}
else
break;
}
}
void HeapPop(Heap* pheap) {
assert(pheap);
assert(!isHeapEmpty(pheap));
//最后一个与根交换
swap(&pheap->arr[0], &pheap->arr[pheap->size - 1]);
pheap->size--;
//下移
AjustDown(pheap->arr, pheap->size, 0);
return;
}
2.5 堆的创建
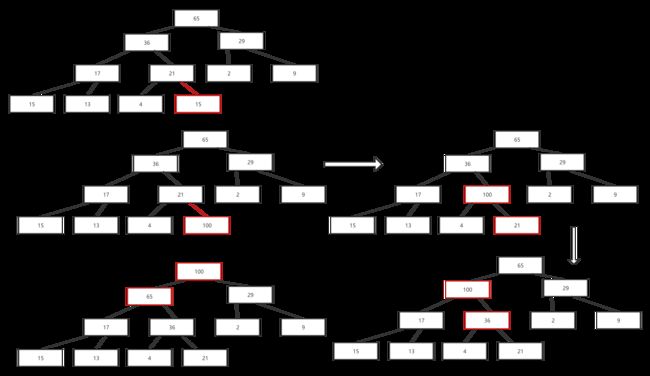
堆的创建有两种方法,一种是逐个插入,另外可以逐渐构建堆直到构建整个堆为止。由于第二种方法的复杂度更低,因此在此介绍第二种方法。该方法即找出最小的父节点,然后对父节点进行循环,从小的堆到大的对,构建好每一个堆。图示与代码如下:
void HeapCreate(Heap* pheap, HeapDataType* arr, size_t len) {
assert(pheap);
HeapDataType* ptemp = (HeapDataType*)malloc(sizeof(HeapDataType) * len);
if (ptemp == NULL) {
perror("malloc");
exit(-1);
}
pheap->arr = ptemp;
memmove(pheap->arr, arr, sizeof(HeapDataType) * len);
pheap->size = len;
pheap->capacity = len;
int endLeaf = pheap->size - 1;
int parent = (endLeaf - 1) / 2;
while (parent >= 0) {
AjustDown(pheap->arr, pheap->size, parent);
parent -= 1;
}
return;
}
**堆的建立时间复杂度分析:**对于逐个插入数据后自顶向下的维护堆结构与从底向上逐步构建根节点维持堆结构两个算法,虽然看起来时间复杂度都是O(nlgn),实际上二者的时间复杂度是存在差异的,仔细观察可以发现,对于每一棵子树的根节点和叶节点的数目差不多,因此遍历的数量会少很多,在此通过计算来分析二者的时间复杂度。以满二叉树举例,便于计算以及分析,计算过程如下:
2.6 其他
HeapDataType HeapTop(Heap* pheap) {
return pheap->arr[0];
}
int HeapSize(Heap* pheap) {
return pheap->size;
}
bool isHeapEmpty(Heap* pheap) {
return pheap->size == 0;
}
三、应用
3.1 堆排序
堆排序的主要思路是通过堆得性质,不断从堆顶进行取值出堆,并保持堆的性质不变。通过升序排序为例,具体思路为,初始化时通过建堆的思路将需要排序的数组建成一个大堆(每次出堆最大值,将其放在末尾),建立好后,将最大值与末尾交换,进行下移算法,保持堆的性质,重复此过程知道所有元素排序完成。
堆排序的第一个细节是思考建立大堆还是小堆,如果为升序,那就是需要大堆,建立大堆可以将堆顶元素与末尾交换,并将数组长度减一,这样对于数组来说,堆的性质不变的,而如果是小堆则无法达成该目的。
对于堆排序的时间复杂度为:O(lgn)
具体代码如下:
void HeapSorted(HeapDataType arr[], int len) {
// 升序
// 变成一个大堆
// 最小子树的根节点
int parent = (len - 1) / 2;
while (parent >= 0) {
AjustDown(arr, len, parent);
parent--;
}
// 将最后一个与第一个互换,向下调整
int length = len;
for (int i = 0; i < len; i++) {
swap(&arr[0], &arr[length - 1]);
AjustDown(arr, --length, 0);
}
return 0;
}
3.2 Top-K问题
TOP-K即求数据中前K个最大的元素或者最小的元素,一般情况下数据量都比较大。一般情况下,如果使用排序的话复杂度会过高,但使用堆的数据结构可以很好的解决该问题。
对于实现思路主要有两种(以求最大值为例):
- 建立一个N个数据的大堆,出堆k次,依次取堆顶,这种方法适用于数据在内存的时候,不会有额外的空间消耗,时间复杂度为 O(N+ Nlgk)
- 建立一个k个数据的小堆,依次遍历数组,比堆顶大的数据就替代堆顶,再向下调整,直到数组遍历完,最后最大的k个数就在小堆中,这种思路直接取部分数据到小堆中,每次出堆最小的,因此最后得到的是前k个大的数,这种方法的时间复杂度为:O(k+(N-k)logk) = O(Nlgk),但时间复杂度为O(K),实际上消耗也很小,但使用与更多长场景。
在此我们对第二种方法对最小值topk问题进行实现,代码示例如下:
void PrintTopK(HeapDataType arr[], int n, int k) {
// 最小k个数
// 建立一个k个数据的大堆
HeapDataType* arr_temp = (HeapDataType*)malloc(sizeof(HeapDataType) * k);
if (arr_temp == NULL) {
perror("arr_temp malloc failed");
exit(1);
}
for (int i = 0; i < k; i++) {
arr_temp[i] = arr[i];
}
Heap* minKHeap = (Heap*)malloc(sizeof(Heap));
HeapInit(minKHeap);
// 遍历数组当有更小的数时,出最大堆数,入数组的数
HeapCreate(minKHeap, arr_temp, k);
for (int i = 0; i < n; i++) {
if (HeapTop(minKHeap) > arr[i]) {
HeapPop(minKHeap);
HeapPush(minKHeap, arr[i]);
}
}
printf("TopK:");
for (int i = 0; i < k; i++) {
printf("%d ", minKHeap->arr[i]);
}
printf("\n");
free(minKHeap);
free(arr_temp);
return;
}
void test4() {
int n = 10000;
int* a = (int*)malloc(sizeof(int) * n);
srand(time(0));
for (size_t i = 0; i < n; ++i)
{
a[i] = rand() % 1000000;
}
a[5] = -1;
a[1231] = -2;
a[531] = -3;
a[5121] = -4;
a[115] = -5;
a[2335] = -6;
a[9999] = -7;
a[76] = -8;
a[423] = -9;
a[3144] = -10;
PrintTopK(a, n, 10);
free(a);
}
补充:
- 代码将会放到:C_C++_REVIEW: 一套 C/C++ 系统完整的使用手册,以及部分疑难杂症的解析 (gitee.com) ,欢迎查看!
- 欢迎各位点赞、评论、收藏与关注,大家的支持是我更新的动力,我会继续不断地分享更多的知识!