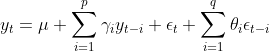用Rstudio进行ARIMA模型预测（小白系列）

读前告知：阅读本文前，需要带着对应用ARIMA模型的需求，大佬请避让，但欢迎指点本文的不足之处，本文只说明ARIMA模型和用Rstudio应用ARIMA模型进行预测的一些通俗性概念和操作，不会深度讲解定义的来源和相关代码的意义，旨在帮助读者搭建理解ARIMA模型实际应用的桥梁，对于一些刨根问底的求知者请转向大佬区域或自行查阅相关资料。

1.ARIMA模型及相关知识点的介绍

1.1ARIMA模型（p,d,q）

     全称：自回归（AR）差分（I）移动平均模型（MA）。p是自回归项，d是时间序列平稳化是做的差分次数，q是移动平均项。在我们生活中有很多的经济现象都具有一定的规律性或者也会发生周期性的变化，然后我们就会利用一些方法来预测经济的未来发展趋势，其中一种方法就是我们这里提到的ARIMA模型，它的原理就是把非平稳的时间序列通过差分转化为平稳的时间序列，然后。其中ARIMA模型包含了以下几种类型：

 1.1.1自回归模型（AR）    

      在计量经济学中，了解基础的人一般大概知道回归分析，通过回归分析可以考察解释变量与被解释变量之间的相关关系，进一步延申到自回归，自回归没有了回归分析中的一个变量与另一个变量的关系，在时间序列中，自回归只有当前值和历史值之间的关系。所以在AR模型中，它用的是过去一段时间数据对未来发生值的预测。不过，自回归模型需要满足的是所使用的时间序列是平稳的而且不是白噪声。（其中平稳性和白噪声将会在下文说明）

   AR模型有个AR（P）过程 ,简单来说就是P阶自回归过程，回归过程的公式定义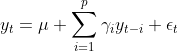：       ，其中是t时刻对应的数据，的常数项,p就是上面说的p阶自回归阶数，是自相关系数（相似于回归模型中求解的，在此模型中，随着时间序列越推后，会越趋近于0），是误差项。主要表达的是当前期受到过去p期的影响，同时也受到随机干扰项（误差项）的冲击，比如说20年的疫情，也可能存在漂移项的冲击。

1.1.2移动平均模型（MA）

    在自回归模型中，有个误差项，它是不同时期内发生的冲击导致时间序列数据的变异，而移动平均模型就是对这些误差项的累加。MA模型有个q阶移动平均过程，移动平均过程的公式定义：

,它表达的是当前期的冲击和（不可观察的）滞后期冲击，通过q值的引入来消除预测中的随机波动；与自回归公式不同之处主要是用当前的冲击和序列的（可以观察到的）之后值来表述

1.1.3自回归移动平均模型（ARMA）

    该模型是AR模型和MA模型的结合；公式：。

1.2平稳性及其检验

    平稳性可以说是时间序列预测前的一个重要指标，通过平稳性检验的时间序列的均值和方差都不会发生明显变化，它能让时间序列有规律可循，并在未来一段时间依照原有的“惯性”继续下去。

1.3差分法

    差分法的原理是时间序列里t期的值与t-1的值的差，通过这个过程能让时间序列更平稳一些，具体的差分次数在ARIMA模型中表示的是d值

1.4白噪声及其检验

    它的特点表现在任何两个时期的随机变量都不相关，时间序列中不存在任何可以利用的规律，所以白噪声序列不能用过去的数据对未来进行预测，在ARIMA模型开始执行的前几部操作中若检测出白噪声序列就说明该时间序列就不能进行下去了，无法对其预测。

    其中白噪声检验又称纯随机性检验，它的作用在ARIMA模型中担当的是检测拟合出来的ARIMA模型是否是优质模型

1.5自相关函数ACF和偏自相关函数PACF

   ACF表示的是在时间序列中不同时间对应的数值之间的相关性，对应的PACF是描述随机特征的一种方法，具体原理内容较多，不便解释。通过这两个函数的图像可以确定ARIMA模型中p,q的值。

在理解一些相关概念后，我们开始进行ARIMA模型的实际操作

2.R和Rstudio的安装

2.1安装R

    ①进入R的官网

R: The R Project for Statistical Computing

    ② 点击DOWNLOAD下的CRAN

    ③下拉选择China的镜像：

The Comprehensive R Archive Networkhttps://mirrors.tuna.tsinghua.edu.cn/CRAN/    ④点击Download R for Windows,再点击 install R for the first time,最后点击Download R 4.1.1 for Windows下载安装

2.2安装Rstudio 

    ①进入Rstudio官网：

RStudio | Open source & professional software for data science teams - RStudio

    ②下拉窗口找到"DOWNLOAD FREE DESKTOP IDE"并点击进去

    ③下拉窗口找到"Rstudio Dsktop"和"Free",点击"DOWNLOAD"

    ④版本选择windows版

     ⑤注意安装的目标文件夹名称都要是英文

     ⑥更新R包镜像资源，点击Tools下的Global Options,在其中选择Packages,最后点击change更改为国内的服务器

3.Rstudio的ARIMA模型实际操作

3.1简化步骤

3.1.1操作原理 

 (此图片源于B站up不懂数据)

3.1.2操作流程

    平稳性检验→白噪声检验→模型拟合与定阶→模型检验→模型预测

3.2ARIMA实际操作

该例子以2010年1月份到2020年12月份中国钢铁出口贸易额（美元）建立表格，然后导入到Rstudio中建立时间序列，之后进行以下一系列操作.......

3.2.1导入数据

    打开Rstudio软件后，在Console框中输入代码安装相关package包

install.packages("forecast")
install.packages("tseries")
install.packages("readxl")

    进行数据的导入和相关算法的引入，其中的getwd(C:/Rstudio/project)是确定你需要预测的表格文件所在的地址，如果不对的话可以在getwd()下一行输入例如：setwd(F:/Rstudio/first project)，具体所要使用的表格所在地址可以鼠标右击桌面表格，查看表格的属性来获取

library(forecast)
library(tseries)
library(readxl)
getwd()                                         #确定工作文件位置
x<-read_excel('abcd.xlsx')                      #读取文件并命名x
x1<-x[,2]                                       #获取表格中第二列的数据，并命x1
xts<-ts(x1,start=2010,end = 2020,frequency = 12)#建立时间序列，12为月度数据，年度数据改为1

3.2.2平稳性检验（ADF单位根检验）

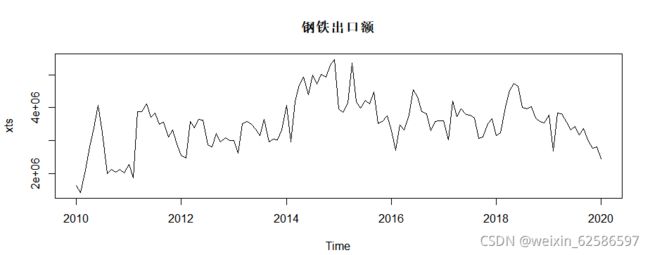
    ①画出时间序列图，命名为xts

plot(xts，main='钢铁出口额')               #原时序图

     ②对原时序xts进行单位根检验，检验出P值大于0.05，存在单位根，说明原时间序列不稳定

ADF<-adf.test(xts)      #原序列单位根检验
ADF                     #P值大于0.05，存在单位根

<单位根检验结果>
       Augmented Dickey-Fuller Test

data:  xts
Dickey-Fuller = -2.6895, Lag order = 4,
p-value = 0.2902
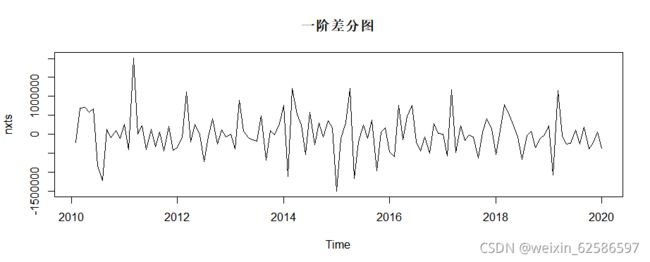
alternative hypothesis: stationary

    ③判断非平稳的原时间序列需要几阶差分化为平稳序列， 结果表明一阶差分，给一阶差分后的时间序列命名为nxts，然后在进行单位根检验其稳定性，结果得出p值小于0.05，拒绝原假设，一阶差分后的时间序列平稳

ndiffs(xts)                               #判断几阶差分化为平稳序列
nxts<-diff(xts,1)                         #一阶差分
plot(nxts，main='一阶差分图’)              #一阶差分图
ADF1<-adf.test(nxts)                      #一阶差分单位根检验
ADF1                                      #P值小于0.05，拒绝原假设，序列平稳

<判断几阶差分>
>  ndiffs(xts)             #判断几阶差分化为平稳序列
[1] 1

<单位根检验结果>
	Augmented Dickey-Fuller Test

data:  nxts
Dickey-Fuller = -6.6148, Lag order = 4,
p-value = 0.01
alternative hypothesis: stationary

3.2.3白噪声检验（纯随机性检验）

    该检验主要判断差分后的时间序列是否具有白噪声，或者说时间序列中的数值随机性很高，且不具备规律性。经检验差分后的序列不是白噪声，可以进行下一步ARIMA模型中p,d,q的确定（模型拟合），如果说差分后序列是白噪声，就说明该序列不具备可以预测的意义了，也说明ARIMA模型不适合对该序列做预测

Box.test(nxts,type = "Ljung-Box")             #P值小于0.05，差分后的序列不是白噪声模型

<白噪声检验结果>
	Box-Ljung test

data:  nxts
X-squared = 5.1063, df = 1, p-value = 0.02384

3.2.4确定ARIMA模型中的p,q

    这里有两种方法，一种是凭对知识点的理解通过ACF函数图和PACF函数图自行判断p,q的值，另一种是通过软件的算法自动预测。这里要注意的是，时间序列有时会呈季节性或者周期性，自动预测的效果会不如自行判断并通过对比找出最优ARIMA模型的效果佳。

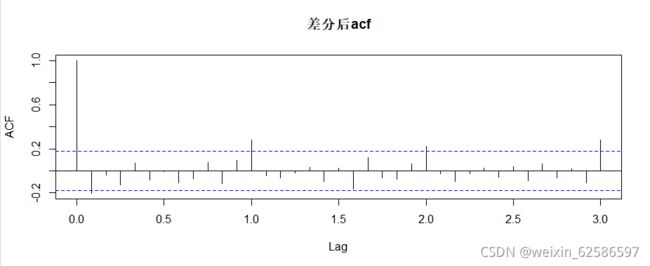
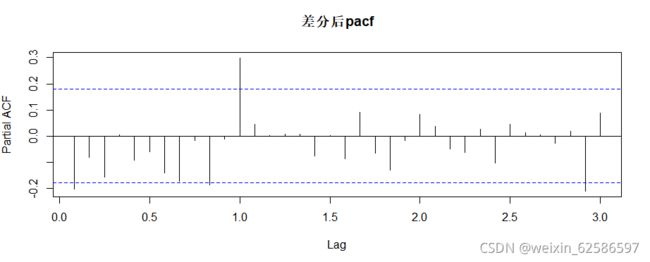
    ①通过自相关图按自身经验来确定；这里的lag,也就是滞后期，需要根据SC或AIC等信息准则，越小越好。判断依据理论格式：

模型	AR(p)	MA(q)	ARMA(p,q)
ACF	拖尾	第q个后截尾	拖尾
PACF	第p个后截尾	拖尾	拖尾

acf(nxts,main='差分后acf',lag.max = 60)
pacf(nxts,main='差分后pacf',lag.max = 60)

 

     ②通过软件算法自动确定，拟合后的模型命名为fit，结果最优模型输出为ARIMA(0,1,1)(2,0,0)[12] 。

fit<-auto.arima(xts)
fit 
arima<-auto.arima(xts,trace=T)
accuracy(fit) 

<拟合模型相关数据>
Series: xts 
ARIMA(0,1,1)(2,0,0)[12] 

Coefficients:
          ma1    sar1    sar2
      -0.3415  0.2934  0.2391
s.e.   0.0962  0.0921  0.1007

sigma^2 estimated as 2.283e+11:  log likelihood=-1739.72
AIC=3487.44   AICc=3487.78   BIC=3498.59

<模型精度的相关数据>
                  ME     RMSE      MAE       MPE       MAPE      MASE       ACF1
Training set -2063.327  469821.2 354179.7  -1.137371   10.34958 0.5273896 0.01337568
                

 <最优模型选择> 
 ARIMA(2,1,2)(1,0,1)[12] with drift         : Inf
 ARIMA(0,1,0)            with drift         : 3510.207
 ARIMA(1,1,0)(1,0,0)[12] with drift         : 3494.535
 ARIMA(0,1,1)(0,0,1)[12] with drift         : 3497.442
 ARIMA(0,1,0)                               : 3508.158
 ARIMA(1,1,0)            with drift         : 3507.238
 ARIMA(1,1,0)(2,0,0)[12] with drift         : 3491.288
 ARIMA(1,1,0)(2,0,1)[12] with drift         : Inf
 ARIMA(1,1,0)(1,0,1)[12] with drift         : Inf
 ARIMA(0,1,0)(2,0,0)[12] with drift         : 3499.315
 ARIMA(2,1,0)(2,0,0)[12] with drift         : 3493.165
 ARIMA(1,1,1)(2,0,0)[12] with drift         : Inf
 ARIMA(0,1,1)(2,0,0)[12] with drift         : 3489.954
 ARIMA(0,1,1)(1,0,0)[12] with drift         : 3493.126
 ARIMA(0,1,1)(2,0,1)[12] with drift         : Inf
 ARIMA(0,1,1)(1,0,1)[12] with drift         : Inf
 ARIMA(0,1,2)(2,0,0)[12] with drift         : 3491.904
 ARIMA(1,1,2)(2,0,0)[12] with drift         : Inf
 ARIMA(0,1,1)(2,0,0)[12]                    : 3487.784
 ARIMA(0,1,1)(1,0,0)[12]                    : 3490.996
 ARIMA(0,1,1)(2,0,1)[12]                    : Inf
 ARIMA(0,1,1)(1,0,1)[12]                    : Inf
 ARIMA(0,1,0)(2,0,0)[12]                    : 3497.176
 ARIMA(1,1,1)(2,0,0)[12]                    : Inf
 ARIMA(0,1,2)(2,0,0)[12]                    : 3489.697
 ARIMA(1,1,0)(2,0,0)[12]                    : 3489.114
 ARIMA(1,1,2)(2,0,0)[12]                    : Inf

 Best model: ARIMA(0,1,1)(2,0,0)[12] 

3.2.5模型检验

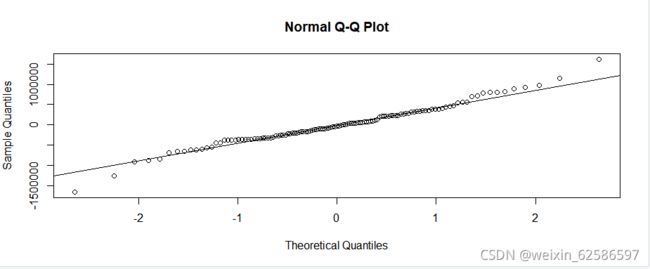
    可以通过画QQ图与其加线的拟合度来判断残差是否服从正态分布，然后再对拟合模型的残差白噪声检验进一步判断残差之间是否相关。从输出结果中看出，残差服从正态分布而且p值大于0.05证明残差之间不相关，可以进行下一步的模型预测。

qqnorm(fit$residuals)                      #QQ图
qqline(fit$residuals)                      #加线
Box.test(fit$residuals,type = "Ljung-Box") #残差白噪声检验

<白噪声检验结果>
Box-Ljung test

data:  fit$residuals
X-squared = 0.022189, df = 1, p-value = 0.8816

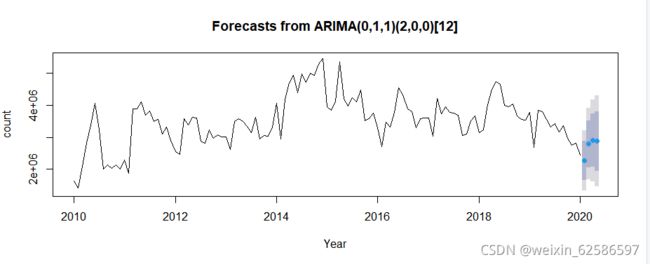
3.2.6模型预测

对原序列进行预测4期的值和预测图像，结果如下表格：

2020年2月	2264079
2020年3月	2788542
2020年4月	2897962
2002年5月	2876895

 #代码汇总

library(forecast)
library(tseries)
library(readxl)
getwd()
x<-read_excel('abcd.xlsx')
x1<-x[,2]
xts<-ts(x1,start=2010,end = 2020,frequency = 12)
#1.检验平稳性
 plot(xts,main='钢铁出口额')               #原时序图
 ADF<-adf.test(xts)      #原序列单位根检验
 ADF                     #P值大于0.05，存在单位根
 ndiffs(xts)             #判断几阶差分化为平稳序列
 nxts<-diff(xts,1)       #一阶差分
 plot(nxts,main='一阶差分图')              #一阶差分图
 ADF1<-adf.test(nxts)    #一阶差分单位根检验
 ADF1                    #P值小于0.05，拒绝原假设，序列平稳
#2.白噪声检验（纯随机性检验）
 Box.test(nxts,type = "Ljung-Box")#P值小于0.05，差分后的序列不是白噪声模型
#3.确定ARIMA(p,d,q)中的p,q
 #①通过自相关图按自身经验来确定
  acf(nxts,main='差分后acf',lag.max = 36)
  pacf(nxts,main='差分后pacf',lag.max = 36)
 #②模型拟合与定阶
  fit<-auto.arima(xts)
  fit 
  arima<-auto.arima(xts,trace=T)
  accuracy(fit) 
#4.模型诊断
 qqnorm(fit$residuals)
 qqline(fit$residuals)  
 Box.test(fit$residuals,type = "Ljung-Box")
#模型预测
 forecast(fit,4)#预测4期
 plot(forecast(fit,4),xlab = "Year",ylab = "count")