线性二分类——机器学习

目录

一、算法思想

 二、算法原理

三、算法分析

四、源程序代码

五、运行结果及分析

六、总结

---

一、算法思想

---

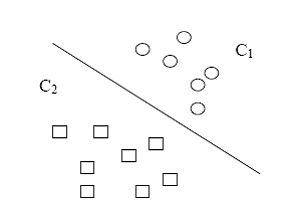
（1）二分类:表示分类任务有两个类别，比如我们想识别图片中是不是狗，也就是说，训练一个分类器，输入一幅图片，用特征向量x表示，输出是不是狗，用y=0或1表示。二类分类是假设每个样本都被设置了一个且仅有一个标签 0 或者 1。

 

（2）多类分类: 表示分类任务中有多个类别, 比如对一堆水果图片分类, 它们可能是橘子、苹果、梨等. 多类分类是假设每个样本都被设置了一个且仅有一个标签: 一个水果可以是苹果或者梨, 但是同时不可能是两者。

（3）多标签分类: 给每个样本一系列的目标标签. 可以想象成一个数据点的各属性不是相互排斥的(一个水果既是苹果又是梨就是相互排斥的), 比如一个文档相关的话题. 一个文本可能被同时认为是宗教、政治、金融或者教育相关话题。

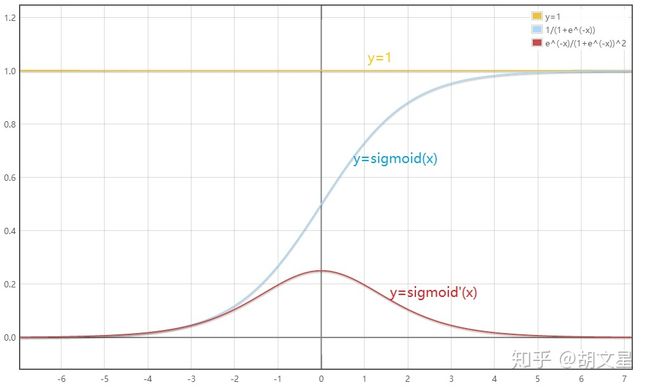
（4）二分类函数：对率函数Logistic Function，本身是激活函数，又可以当作二分类的分类函数。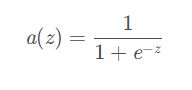

 

此函数实际上是一个概率计算，它把[ − ∞ , ∞ ]之间的任何数字都压缩到[0,1]之间，返回一个概率值。这就是它的工作原理。

 二、算法原理

---

        训练时，一个样本x在经过神经网络的最后一层的矩阵运算后的结果作为输入，经过Sigmoid后，输出一个[0,1]之间的预测值。

        我们假设这个样本的标签值为0（属于负类，另外一类是第1类属于正类），如果其预测值越接近0，就越接近标签值，那么误差越小，反向传播的力度就越小。

        推理时，我们预先设定一个阈值，比如上图中的红线，我们设置阈值=0.5，则当推理结果大于0.5时，认为是正类；小于0.5时认为是负类；等于0.5时，根据情况自己定义。

        阈值也不一定就是0.5，也可以是0.65等等，阈值越大，准确率越高，召回率越低；阈值越小则相反。

三、算法分析

---

(1)、先进行正向计算，如z=x1w1+x2w2+b

(2)、然后进行分类计算a=1/(1+e^z)

(3)、损失函数计算loss=-[yln(a)+(1-y)ln(1-a)]

(4)、根据loss的值来判断分类情况是否正确

四、源程序代码

---

import matplotlib.pyplot as plt
import numpy as np
from sklearn.metrics import classification_report
from sklearn import tree
import graphviz
#载入数据
data = np.genfromtxt('.csv',delimiter=',')
x_data = data[:,:-1]
y_data = data[:,-1]
plt.scatter(x_data[:,0],x_data[:,-1],c=y_data)
plt.show()
#创建决策树模型
model = tree.DecisionTreeClassifier()
model.fit(x_data,y_data)
#导出决策树
dot_data = tree.export_graphviz(model,
                                out_file=None,
                                #特征的名字，要设置
                                feature_names = ['x','y'],
                                class_names=['label0','label1'],
                                filled=True,
                                rounded=True,
                                special_characters=True)
graph = graphviz.Source(dot_data)
graph.render('cart_1')
#获取数据值所在范围
x_min,x_max = x_data[:,0].min() - 1,x_data[:,0].max() + 1
y_min,y_max = x_data[:,1].min() - 1,x_data[:,1].max() + 1
 
#生成网格矩阵
xx,yy = np.meshgrid(np.arange(x_min,x_max,0.02),
                    np.arange(y_min,y_max,0.02))
z = model.predict(np.c_[xx.ravel(),yy.ravel()])
#扁平化，得到一个一个的点
#ravel和flatten类似，多维数据转一维，flatten不会改变原始数据，而ravel会
z = z.reshape(xx.shape)
#等高线图
#在这里，只有两个高度，0和1
cs = plt.contourf(xx,yy,z)
#样本散点图
plt.scatter(x_data[:,0],x_data[:,1],c=y_data)
plt.show()

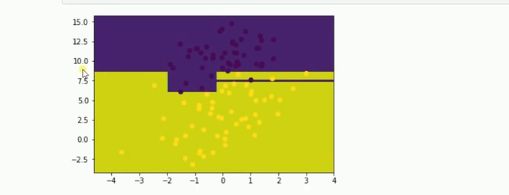
五、运行结果及分析

---

 

由图可见，数据几乎被一条线分隔为两部分

六、总结

---

        通过本次实验的学习，基本可以实现线性二分类。通过对该方法的学习，发现相同的模型在不同的终止方式、不同的训练次数、损失、梯度的情况下有不同的效果。

        特别是数据标准化前和标准化后的处理有很大的差异，所以要多尝试不同的指定参数。详细的分析方式在之后的内容中介绍。