深度学习入门---《白话机器学习的数学》笔记

---

一、基础：回归的实现

1、训练数据click.csv

x,y
235,591
216,539
148,413
35,310
85,308
204,519
49,325
25,332
173,498
191,498
134,392
99,334
117,385
112,387
162,425
272,659
159,400
159,427
59,319
198,522

2、参考公式：

首先把 fθ(x) 作为一次函数来实现

参数更新表达式：

学习率先设置为10−3 。

3、代码实现：

'''
回归的实现
'''
import numpy as np
import matplotlib.pyplot as plt

# 读入训练数据
train = np.loadtxt('click.csv',delimiter=',',skiprows=1)
train_x = train[:,0]
train_y = train[:,1]

# 参数初始化
theta0 = np.random.rand()
theta1 = np.random.rand()
# 预测函数
def f(x):
    return  theta0 + theta1 * x
# 目标函数
def E(x,y):
    return 0.5 * np.sum((y - f(x))**2)
# 标准化
mu = train_x.mean()
sigma = train_x.std()
def standardize(x):
    return (x - mu)/sigma
train_z = standardize(train_x)

# 绘图
# plt.plot(train_z,train_y,'o')
# plt.show()

# 学习率
ETA = 1e-3
# 误差的差值
diff = 1
# 更新次数
count = 0

# 直到误差的值小于0.01为止，重复参数更新
error = E(train_z, train_y)
while diff > 1e-2:
    # 更新结果保存到临时变量
    tmp0 = theta0 - ETA * np.sum((f(train_z) - train_y))
    tmp1 = theta1 - ETA * np.sum((f(train_z) - train_y) * train_z)
    # 更新参数
    theta0 = tmp0
    theta1 = tmp1
    # 计算与上一次误差的差值
    current_error = E(train_z,train_y)
    diff = error - current_error
    error = current_error
    # 输出日志
    count += 1
    log = '第{}次：theta0 = {:.3f},theta1 = {:.3f},差值 = {:.4f}'
    # print(log.format(count,theta0,theta1,diff))

# 绘图确认
x = np.linspace(-3, 3, 100)
plt.plot(train_z,train_y,'o')
plt.plot(x,f(x))
# plt.show()
# print(f(standardize(100)))

4、运行结果：

5、验证：

二、多项式回归

提示：增加参数theta2，并替换预测函数
多重回归：将参数和训练数据都作为向量来处理，使计算变得简单

1、参考公式

将参数和训练数据都作为向量来处理，可以使计算变得更简单

由于训练数据有很多，所以我们把 1 行数据当作 1 个训练数据，以矩阵的形式来处理会更好

2、代码实现

'''
多项式回归
增加参数theta2，并替换预测函数
多重回归：将参数和训练数据都作为向量来处理，使计算变得简单
'''
import numpy as np
import matplotlib.pyplot as plt
# 读入训练数据
train = np.loadtxt('click.csv',delimiter=',',skiprows=1)
train_x = train[:,0]
train_y = train[:,1]
# 标准化
mu = train_x.mean()
sigma = train_x.std()
def standardize(x):
    return (x - mu)/sigma
train_z = standardize(train_x)

# 初始化参数
theta = np.random.rand(3)
# 学习率
ETA = 1e-3
# 误差的差值
diff = 1
# 均方误差的历史记录
errors = []

# 创建训练数据的矩阵
def to_matrix(x):
    return  np.vstack([np.ones(x.shape[0]),x,x ** 2]).T
X = to_matrix(train_z)


# 预测函数
def f(x):
    return np.dot(x,theta)
# 目标函数
def E(x,y):
    return 0.5 * np.sum((y - f(x))**2)
# 均方误差
def MSE(x, y):
    return (1 / x.shape[0]) * np.sum((y - f(x)) ** 2)


# 重复学习
error = E(X, train_y)
errors.append(MSE(X, train_y))
while diff > 1e-2:
    # 更新参数
    theta = theta - ETA * np.dot(f(X) - train_y,X)
    # 计算与上一次误差的差值
    current_error = E(X, train_y)
    diff = error - current_error
    error = current_error

    errors.append(MSE(X, train_y))
    # diff = errors[-2] - errors[-1]

# 绘制拟合曲线
x = np.linspace(-3,3,100)
plt.plot(train_z,train_y,'o')
plt.plot(x,f(to_matrix(x)))
plt.show()

# 绘制误差变化图
x = np.arange(len(errors))
plt.plot(x, errors)
plt.show()

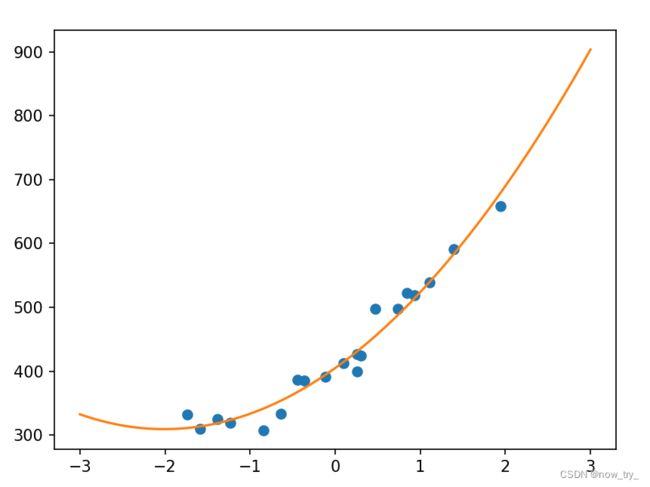
3、运行结果

绘制误差变化图：

三、随机梯度下降法的实现

1、参考公式

在随机梯度下降法中会随机选择一个训练数据并使用它来更新参数。表达式中的 k 就是被随机选中的数据索引。

随机梯度下降法由于训练数据是随机选择的，更新参数时使用的又是选择数据时的梯度，所以不容易陷入目标函数的局部最优解。

小批量（mini-batch）梯度下降法

前面提到了随机选择 1 个训练数据的做法，此外还有随机选择 m 个训练数据来更新参数的做法。设随机选择 m 个训练数据的索引的集合为 K：

2、代码实现

"""
随机梯度下降法的实现
"""
import numpy as np
import matplotlib.pyplot as plt
# 读入训练数据
train = np.loadtxt('click.csv',delimiter=',',skiprows=1)
train_x = train[:,0]
train_y = train[:,1]
# 标准化
mu = train_x.mean()
sigma = train_x.std()
def standardize(x):
    return (x - mu)/sigma
train_z = standardize(train_x)

# 初始化参数
theta = np.random.rand(3)
# 均方误差的历史记录
errors = []
# 误差的差值
diff = 1
# 学习率
ETA = 1e-3

# 创建训练数据的矩阵
def to_matrix(x):
    return  np.vstack([np.ones(x.shape[0]),x,x ** 2]).T
X = to_matrix(train_z)

# 预测函数
def f(x):
    return np.dot(x,theta)
# 目标函数
def E(x,y):
    return 0.5 * np.sum((y - f(x))**2)
# 均方误差
def MSE(x, y):
    return (1 / x.shape[0]) * np.sum((y - f(x)) ** 2)

# 重复学习
errors.append(MSE(X, train_y))
while diff > 1e-2:
    # 为了调整训练数据的顺序，准备随机的序列permutation
    p = np.random.permutation(X.shape[0])
    # 随机取出训练数据，使用随机梯度下降法更新参数
    for x,y in zip(X[p,:],train_y[p]):
        theta = theta - ETA * (f(x) - y) * x
    # 计算与上一次误差的差值
    errors.append(MSE(X, train_y))
    diff = errors[-2] - errors[-1]

x = np.linspace(-3,3,100)
plt.plot(train_z,train_y,'o')
plt.plot(x,f(to_matrix(x)))
plt.show()

3、运行结果

四、感知机

1、训练数据images1.csv

x1,x2,y
153,432,-1
220,262,-1
118,214,-1
474,384,1
485,411,1
233,430,-1
369,361,1
484,349,1
429,259,1
286,220,1
399,433,-1
403,340,1
252,34,1
497,472,1
379,416,-1
76,163,-1
263,112,1
26,193,-1
61,473,-1
420,253,1

2、参考公式

感知机模型

判别函数

根据参数向量 x 来判断图像是横向还是纵向的函数，即返回 1 或者 −1 的函数 fw(x)的定义如下。

内积是衡量向量之间相似程度的指标。结果为正，说明二者相似；为 0 则二者垂直；为负则说明二者不相似。

权重向量的更新表达式

3、代码实现

使权重向量成为法线向量的直线方程是内积为 0 的 x 的集合。所以对它进行移项变形，最终绘出以下表达式的图形即可。

"""
分类---感知机
"""
import numpy as np
import matplotlib.pyplot as plt
# 读入训练数据
train = np.loadtxt('images1.csv',delimiter=',',skiprows=1)
train_x = train[:,0:2]
train_y = train[:,2]
# print(list(zip(train_x,train_y)))


# 权重初始化
# 返回一个或一组服从“0~1”均匀分布的随机样本值。随机样本取值范围是[0,1)，不包括1
w = np.random.rand(2)
#判别函数
def f(x):
    if np.dot(w,x) >= 0:
        return 1
    else:
        return -1

# 重复次数
epoch = 10
# 更新次数
count = 0
# 学习权重
for _ in range(epoch):
    for x,y in zip(train_x,train_y):
        if f(x) != y:
            w = w + y * x
            # 输出日志
            count += 1
            print("第{}次：w = {}".format(count,w))

# 绘制直线：使权重向量称为法线向量的直线方程是内积为0的x的集合
x1 = np.arange(0,500)
plt.plot(train_x[train_y == 1,0], train_x[train_y == 1,1],'o')
plt.plot(train_x[train_y == -1,0], train_x[train_y == -1,1],'x')
plt.plot(x1, -w[0]/w[1]*x1,linestyle = 'dashed')
# plt.axis('scaled')
# plt.show()

print(f([200,100]))

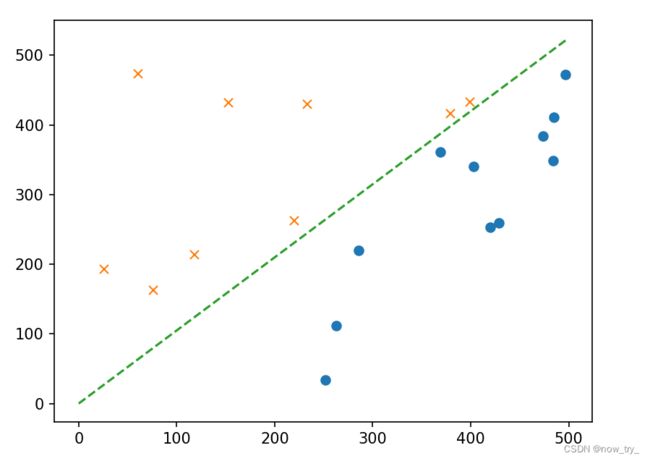
4、运行结果

5、验证

五、分类——逻辑回归的实现

1、训练数据images2.csv

x1,x2,y
153,432,0
220,262,0
118,214,0
474,384,1
485,411,1
233,430,0
369,361,1
484,349,1
429,259,1
286,220,1
399,433,0
403,340,1
252,34,1
497,472,1
379,416,0
76,163,0
263,112,1
26,193,0
61,473,0
420,253,1

2、参考公式

与感知机的不同之处在于，逻辑回归是把分类作为概率来考虑的。

sigmoid函数

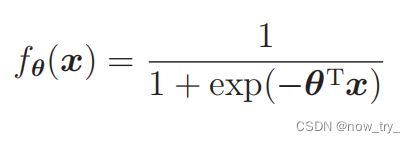
决策边界：
从图中可以看出在 fθ(x) ⩾ 0.5 时，θTx ⩾ 0，反过来在 fθ(x) < 0.5 时，θTx < 0;

参数更新表达式

3、代码实现

首先初始化参数，然后对训练数据标准化。x1和 x2 要分别标准 化。另外不要忘了加一个 x0 列。
θTx = 0这条直线是决策边界

"""
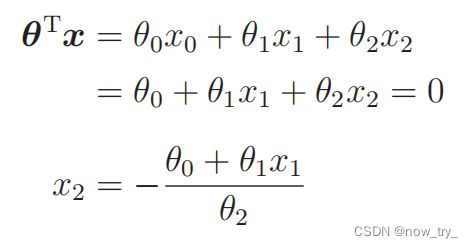
分类：逻辑回归的实现
"""
import numpy as np
import matplotlib.pyplot as plt
# 读入训练数据
train = np.loadtxt('images2.csv',delimiter=',',skiprows=1)
train_x = train[:,0:2]
train_y = train[:,2]

# 初始化参数
theta = np.random.rand(3)
# 标准化:对x1和x2分别取平均值和标准差，进行标准化
mu = train_x.mean(axis = 0)
sigma = train_x.std(axis = 0)
def standardize(x):
    return (x - mu)/sigma
train_z = standardize(train_x)

# 增加x0
def to_matrix(x):
    x0 = np.ones([x.shape[0], 1])
    return np.hstack([x0, x])

X = to_matrix(train_z)

# sigmoid函数
def f(x):
    return 1/(1 + np.exp(-np.dot(x, theta)))

# 学习率
ETA = 1e-3
# 重复次数
epoch = 5000
# 更新次数
count = 0
# 重复学习
for _ in range(epoch):
    theta = theta - ETA * np.dot(f(X) - train_y, X)
    # 日志输出
    count += 1
    print('第{}次：theta = {}'.format(count,theta))


# 验证：对预测数据进行标准化
# f(to_matrix(standardize([
#     [200,100], # 200x100的横向图像
#     [100,200]  # 100x200的纵向图像
# ])))
def classify(x):
    return (f(x) >= 0.5).astype(np.int)
rst = classify(to_matrix(standardize([
        [200,100], # 200x100的横向图像
        [100,200]  # 100x200的纵向图像
])))
# print(rst)
x1 = np.linspace(-2,2,100)
# 将标准化后的训练数据画成图
plt.plot(train_z[train_y == 1, 0], train_z[train_y == 1, 1], 'o')
plt.plot(train_z[train_y == 0, 0], train_z[train_y == 0, 1], 'x')
plt.plot(x1, -(theta[0] + theta[1] * x1) / theta[2], linestyle = "dashed")
plt.show()

4、运行结果

5、验证

六、线性不可分分类的实现

1、训练数据data3.csv

x1,x2,y
0.54508775,2.34541183,0
0.32769134,13.43066561,0
4.42748117,14.74150395,0
2.98189041,-1.81818172,1
4.02286274,8.90695686,1
2.26722613,-6.61287392,1
-2.66447221,5.05453871,1
-1.03482441,-1.95643469,1
4.06331548,1.70892541,1
2.89053966,6.07174283,0
2.26929206,10.59789814,0
4.68096051,13.01153161,1
1.27884366,-9.83826738,1
-0.1485496,12.99605136,0
-0.65113893,10.59417745,0
3.69145079,3.25209182,1
-0.63429623,11.6135625,0
0.17589959,5.84139826,0
0.98204409,-9.41271559,1
-0.11094911,6.27900499,0

2、代码实现

这个数据看上去不能用一条直线来分类，要用二次函数
对于有4个参数的公式变形：

"""
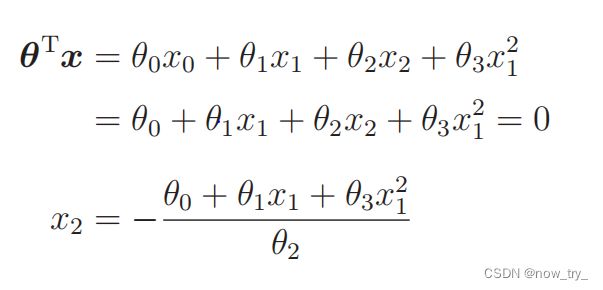
线性不可分分类的实现
"""
import numpy as np
import matplotlib.pyplot as plt

# 读入训练数据
train = np.loadtxt('data3.csv',delimiter=',',skiprows=1)
train_x = train[:,0:2]
train_y = train[:,2]

# 参数初始化
theta = np.random.rand(4)
# 标准化:对x1和x2分别取平均值和标准差，进行标准化
mu = train_x.mean(axis = 0)
sigma = train_x.std(axis = 0)
def standardize(x):
    return (x - mu)/sigma
train_z = standardize(train_x)

# 数据看上去确实不能用一条直线来分类，要用二次函数，在训练数据里加上 x1的平方 就能很好地分类了。
# 增加x0和x3
def to_matrix(x):
    x0 = np.ones([x.shape[0], 1])
    # 增加维度：np.newaxis 放在哪个位置，就会给哪个位置增加维度
    # x[:, np.newaxis] ，放在后面，会给列上增加维度
    x3 = x[:,0,np.newaxis] ** 2
    return np.hstack([x0, x, x3])

X = to_matrix(train_z)

# sigmoid函数
def f(x):
    return 1/(1 + np.exp(-np.dot(x, theta)))

def classify(x):
    return (f(x) >= 0.5).astype(np.int64)

# 学习率
ETA = 1e-3
# 重复次数
epoch = 5000
# 更新次数
count = 0
# 将重复次数作为横轴，精度作为纵轴来绘图，可以看到精度上升
# 精度的历史记录
accuracies = []
# 重复学习
for _ in range(epoch):
    theta = theta - ETA * np.dot(f(X) - train_y, X)
    # 日志输出
    count += 1
    # print('第{}次：theta = {}'.format(count,theta))
    # 计算现在的精度
    result = classify(X) == train_y
    accurancy = len(result[result == True]) / len(result)
    accuracies.append(accurancy)

# 将精度画成图
x = np.arange(len(accuracies))
plt.plot(x,accuracies)
plt.show()

# 将结果画成图
x1 = np.linspace(-2, 2, 100)
x2 = -(theta[0] + theta[1]*x1 + theta[3] * x1 ** 2)/theta[2]
plt.plot(train_z[train_y == 1, 0], train_z[train_y == 1, 1], 'o')
plt.plot(train_z[train_y == 0, 0], train_z[train_y == 0, 1], 'x')
plt.plot(x1,x2,linestyle='dashed')
# plt.show()

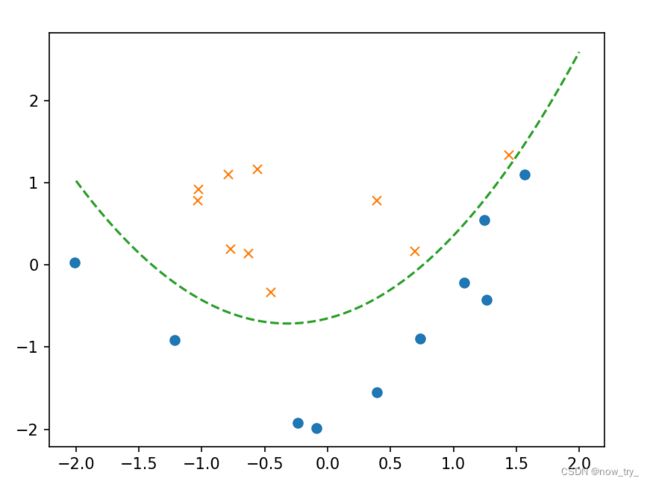
3、运行结果

绘制精度上升曲线

根据公式：

4、用随机梯度下降法实现

"""
随机梯度下降法的实现
"""
import numpy as np
import matplotlib.pyplot as plt

# 读入训练数据
train = np.loadtxt('data3.csv',delimiter=',',skiprows=1)
train_x = train[:,0:2]
train_y = train[:,2]

# 参数初始化
theta = np.random.rand(4)
# 标准化:对x1和x2分别取平均值和标准差，进行标准化
mu = train_x.mean(axis = 0)
sigma = train_x.std(axis = 0)
def standardize(x):
    return (x - mu)/sigma
train_z = standardize(train_x)

# 增加x0和x3
def to_matrix(x):
    x0 = np.ones([x.shape[0], 1])
    # 增加维度
    x3 = x[:,0,np.newaxis] ** 2
    return np.hstack([x0, x, x3])

X = to_matrix(train_z)
print(X)
# sigmoid函数
def f(x):
    return 1/(1 + np.exp(-np.dot(x, theta)))

def classify(x):
    return (f(x) >= 0.5).astype(np.int64)

# 学习率
ETA = 1e-3
# 重复次数
epoch = 5000
# 更新次数
count = 0
# 将重复次数作为横轴，精度作为纵轴来绘图，可以看到精度上升
# 精度的历史记录
accuracies = []
# 重复学习
for _ in range(epoch):
    # 使用随机梯度下降法更新参数
    p = np.random.permutation(X.shape[0])
    for x,y in zip(X[p,:], train_y[p]):
        theta = theta - ETA * (f(x) - y)*x

# 将结果画成图
x1 = np.linspace(-2, 2, 100)
x2 = -(theta[0] + theta[1]*x1 + theta[3] * x1 ** 2)/theta[2]
plt.plot(train_z[train_y == 1, 0], train_z[train_y == 1, 1], 'o')
plt.plot(train_z[train_y == 0, 0], train_z[train_y == 0, 1], 'x')
plt.plot(x1,x2,linestyle='dashed')
plt.show()

# Iris 数据集也可以用在分类上，可以用它进行更多尝试

运行结果：

七、正则化

1、准备工作

自定义函数，并加入一些噪声数据：
虚线就是正确的 g(x) 的图形，圆点就是加入了一点噪声的训练数据：

假设用 10 次多项式来学习这个训练数据。10 次多项式，包括参数 θ0 在内，一共有 11 个参数。

2、代码实现

"""
正则化的实现
"""
import numpy as np
import matplotlib.pyplot as plt
# 真正的函数
def g(x):
    return 0.1 * (x ** 3 + x ** 2 + x)
# 随意准备一些向真正的函数加入了一点噪声的训练数据
train_x = np.linspace(-2,2,8)
train_y = g(train_x) + np.random.randn(train_x.size) * 0.05

# 标准化
mu = train_x.mean(axis = 0)
sigma = train_x.std(axis = 0)
def standardize(x):
    return (x - mu)/sigma
train_z = standardize(train_x)

# 创建训练数据的矩阵，假设我们用 10 次多项式来学习这个训练数据。
# 按垂直方向（行顺序）堆叠数组构成一个新的数组.堆叠的数组需要具有相同的维度
def to_matrix(x):
    return np.vstack([
        np.ones(x.size),
        x,
        x ** 2,
        x ** 3,
        x ** 4,
        x ** 5,
        x ** 6,
        x ** 7,
        x ** 8,
        x ** 9,
        x ** 10,
    ]).T

X = to_matrix(train_z)
# 参数初始化
# X.shape[1]：有几列
# randn是从标准正态分布中返回一个或多个样本值。正态分布,也即这些随机数的期望为0,方差为1;
# rand则会产生[0, 1)之间的随机数

theta = np.random.randn(X.shape[1])
# 预测函数
def f(x):
    return np.dot(x, theta)

# 绘图确认
x = np.linspace(-2,2,100)
# plt.plot(train_x,train_y,'o')
# plt.plot(x,g(x),linestyle='dashed')
# plt.ylim(-1,2)
# plt.show()

# 学习率
ETA = 1e-4
# 误差
diff1 = 1
# 目标函数
def E(x,y):
    return 0.5 * np.sum((y - f(x)) ** 2)
# 重复学习
error = E(X, train_y)

'''不应用正则化的实现'''
''''''
while diff1 > 1e-6:
    theta = theta - ETA * np.dot(f(X)-train_y,X)
    current_error1 = E(X, train_y)
    diff1 = error - current_error1
    error = current_error1

z = standardize(x)
plt.plot(train_z,train_y,'o')
plt.plot(z, f(to_matrix(z)),linestyle='dashed')
plt.show()


'''应用了正则化的实现'''
'''
# 保存未正则化的参数，然后再次参数初始化
theta1 = theta
theta = np.random.randn(X.shape[1])
# 正则化常量
LAMBDA = 1
# 误差
diff2 = 1

while diff2 > 1e-6:
    # 正则化项。偏置项不适用正则化，所以为0
    reg_term = LAMBDA * np.hstack([0,theta[1:]])
    # 应用正则化项，更新参数
    theta = theta - ETA * (np.dot(f(X)-train_y,X) + reg_term)
    current_error2 = E(X, train_y)
    diff2 = error - current_error2
    error = current_error2

# 对结果绘图
z = standardize(x)
plt.plot(train_z,train_y,'o')
plt.plot(z, f(to_matrix(z)))
plt.show()
'''

3、运行结果

未应用正则化的实现

应用了正则化的实现

绘制在一起进行比较：