Python/OpenCV 使用傅里叶变换与高斯平滑分析轮廓轨迹

该方法基本思想是通过分析高低频信息检测出轮廓碰伤、运动轨迹突变等信息，在工业上应用可能比较广泛， 对各种不规则形状都能分析，不过对高频信息多的复杂形状可能不好区分形状与噪音。

在这个例子中讲使用一个有鼓包的鸡蛋

import numpy as np
from scipy.ndimage import gaussian_filter1d
import matplotlib.pyplot as plt
import cv2 as cv
img = cv.imread('egg_flawed.jpg',0)
h, w = img.shape[:2]

二值化之后成为上图

ret,thresh = cv.threshold(img,200,255,cv.THRESH_BINARY_INV)

在充填，使用重心找到一个中心之后进行极坐标转换（这里偷懒没有充填，重心可能偏一点，影响不大）因为方便取值所以讲转换后图形旋转90°

contours, hierarchy = cv.findContours(thresh, cv.RETR_LIST, cv.CHAIN_APPROX_NONE)
M = cv.moments(contours[0])
center = (int(M["m10"] / M["m00"]),int(M["m01"] / M["m00"]))
print(f'found center: {center}')
pol = cv.warpPolar(thresh,(h*2,w*2),center,h,cv.WARP_POLAR_LINEAR| cv.WARP_FILL_OUTLIERS)
pol = cv.rotate(pol, cv.ROTATE_90_CLOCKWISE)

 之后讲外轮廓拟合成为不连续1维函数（这里偷懒直接取了最大值，不适合所有场景，懒得优化糊了一个for应该效率很低，这里不赘述）

contours, hierarchy = cv.findContours(pol, cv.RETR_TREE, cv.CHAIN_APPROX_NONE)
contour_image = np.zeros((h*2,w*2))
cv.drawContours(contour_image, contours, contourIdx=-1, color=255,thickness=1)
discrete_function = np.zeros(w*2).astype(float)

#get max value
for pts in contours[0]:
	x,y = pts[0]
	if y > discrete_function[x]:
		discrete_function[x] = y

在获取一个代表函数的1维数组之后，使用傅里叶变换，并对高频段进行高斯平滑，频率的高低根据实际物体和检测灵敏度决定

sp = np.fft.fft(discrete_function)
freq = np.fft.fftfreq(discrete_function.size)
# plt.plot(freq, sp.real, freq, sp.imag)
# plt.plot(sp)
l,h = 30,int(len(sp)/2)
sp_gauss = sp.copy()
sp_gauss[l:h] = gaussian_filter1d(sp[l:h], 1)
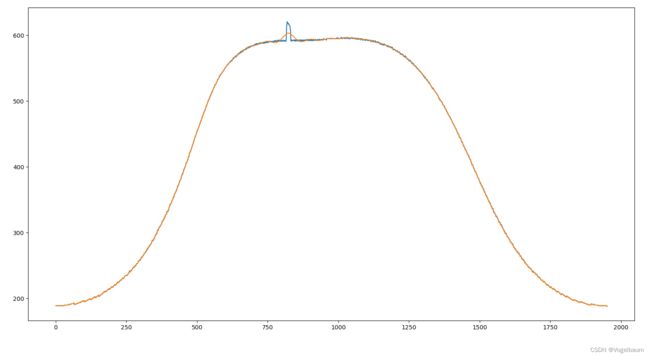
sp_gauss[-h:-l] = gaussian_filter1d(sp[-h:-l], 1)

平滑后绘制函数可以明显看到轮廓鼓包部分与剩余部分有明显差值（蓝色为原函数）

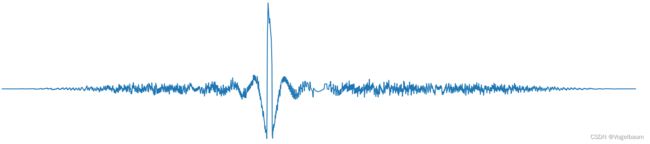
这里通过差值进行阈值处理就能找出鼓包的部分，如果要找出准确位置可以通过逆向极转换转化到原图

这里再补一张没有缺陷分析出来的函数，差值非常小

这里用差值不足应该比较明显，差值过于灵敏，可考虑使用点到函数最短距离或者传入机器学习分类。

全部代码见下

import numpy as np
from scipy.ndimage import gaussian_filter1d
import matplotlib.pyplot as plt
import cv2 as cv

img = cv.imread('egg.jpg',0)
h, w = img.shape[:2]


ret,thresh = cv.threshold(img,200,255,cv.THRESH_BINARY_INV)

contours, hierarchy = cv.findContours(thresh, cv.RETR_LIST, cv.CHAIN_APPROX_NONE)
M = cv.moments(contours[0])
center = (int(M["m10"] / M["m00"]),int(M["m01"] / M["m00"]))
print(f'found center: {center}')

pol = cv.warpPolar(thresh,(h*2,w*2),center,h,cv.WARP_POLAR_LINEAR| cv.WARP_FILL_OUTLIERS)
pol = cv.rotate(pol, cv.ROTATE_90_CLOCKWISE)



contours, hierarchy = cv.findContours(pol, cv.RETR_TREE, cv.CHAIN_APPROX_NONE)
contour_image = np.zeros((h*2,w*2))
cv.drawContours(contour_image, contours, contourIdx=-1, color=255,thickness=1)
discrete_function = np.zeros(w*2).astype(float)

#get max value
for pts in contours[0]:
	x,y = pts[0]
	if y > discrete_function[x]:
		discrete_function[x] = y

cv.namedWindow('img',cv.WINDOW_NORMAL)
cv.namedWindow('pol',cv.WINDOW_NORMAL)
cv.namedWindow('contImage',cv.WINDOW_NORMAL)
cv.namedWindow('thresh',cv.WINDOW_NORMAL)
cv.imshow('img',img)
cv.imshow('thresh',thresh)
cv.imshow('contImage',contour_image)
cv.imshow('pol',pol)
cv.waitKey(0)
# exit()



sp = np.fft.fft(discrete_function)
freq = np.fft.fftfreq(discrete_function.size)
# plt.plot(freq, sp.real, freq, sp.imag)
# plt.plot(sp)
l,h = 30,int(len(sp)/2)
sp_gauss = sp.copy()
sp_gauss[l:h] = gaussian_filter1d(sp[l:h], 1)
sp_gauss[-h:-l] = gaussian_filter1d(sp[-h:-l], 1)

ifft = np.fft.ifft(sp)
ifft2 = np.fft.ifft(sp_gauss)

# plt.plot(freq, sp.real, freq, sp.imag)
plt.plot(freq, sp_gauss.real, freq, sp_gauss.imag)
plt.show()
plt.plot(ifft)
plt.plot(ifft2)
plt.show()
diviation = ifft - ifft2
plt.plot(diviation)
plt.show()