聚类算法学习——K-means

聚类算法学习

导师给安排的方向发生改变，因此需要深入学习这部分内容，这系列就当作学习记录吧。

---

**第一节K-means学习**

---

前言

物以类聚，人以群分。
以下为学习笔记整理

---

一、聚类是什么？

通过无监督学习或者半监督学习，把一群关系紧密存在着不同的样本进行亚群体划分。这里的关系紧密可以是指他们来自同一数据集，表示着相同的事物含义，以至于人们不能把他们进行区分的关系。通过挖掘这些样本数据中的数学统计量关系和特征提取，达到划分为不同的簇的目的。

二、K-means算法

1.算法介绍

K-means算法是一种使用广泛的最基础的聚类算法,K意思是划分的簇数，means记为求取平均的意思，这里的平均稍后单独解释一下。
算法流程是：

1. 选择要聚类的簇数K
2. 生成K个聚类中心点。这里的中心点可以人为规定可以随机生成，不同的初始点会对后续迭代产生影响。中心点就是一个簇的质心，该簇内所有点到此质心的距离一定小于到其他任意簇质心的距离
3. 计算每个样本点到每个质心的距离，并进行比较之后将该样本归于距离最小的质心代表的簇内。这里的距离通常选择欧氏距离。
4. 完成初始化并聚类一次之后，得到一次聚类簇的结果，然后进行质心的更迭。选择将一个簇内所有样本的均值位置作为更迭之后的质心位置，这也就是means的意思。
5. 重复第4部，直到完全收敛。这里的收敛可以人为规定迭代次数，更通常的理解是，质心发生的移动可以忽略不计时，收敛完成。

K-means算法一般作为掌握聚类算法的第一个算法，较为简单，且python语言提供了相当全的API，但直接调用API并不能get到这个算法流程的清晰思路，因此按照上述流程可以直接上手编程一份你自己K-means算法。

2.代码实现

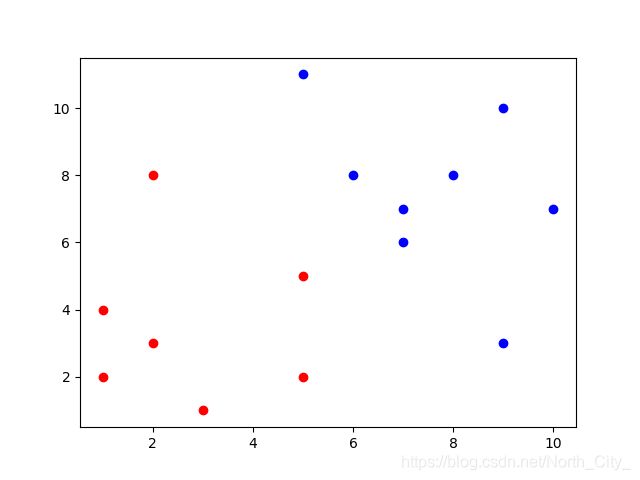
下面是我随便敲出的一些数据，按照他的算法流程进行coding（我受c语言荼毒已久），最后通过画图显示聚类结果：

 data = [[7, 7], [2, 3], [6, 8], [1, 4], [1, 2], [3, 1], [8, 8], [9, 10],
        [10, 7], [5, 5], [7, 6], [9, 3], [2, 8], [5, 11], [5, 2]]
data = np.array(data)
K = 2  # 聚类个数
# 初始质心位置
K1_x = 2
K1_y = 3
K2_x = 7
K2_y = 7
cycle = 20 # 迭代次数
num = 0
while num < cycle:
    num = num + 1 # 进行迭代
    name1 = []
    name2 = []
    for i in range(len(data)):
        dis_1 = np.sqrt(np.square(data[i, 0] - K1_x) + np.square(data[i, 1] - K1_y))#计算两个欧式距离
        dis_2 = np.sqrt(np.square(data[i, 0] - K2_x) + np.square(data[i, 1] - K2_y))
        if dis_1 < dis_2:#进行分类
            name1.append(data[i, :])
        else:
            name2.append(data[i, :])
    print(K1_x, K1_y, K2_x, K2_y) # 观察质心的迭代情况
    name1 = np.array(name1)
    name2 = np.array(name2)
    # 更新质心位置
    K1_x = sum(name1[:, 0]) / len(name1)
    K1_y = sum(name1[:, 1]) / len(name1)
    K2_x = sum(name2[:, 0]) / len(name2)
    K2_y = sum(name2[:, 1]) / len(name2)

# plot
cm = mpl.colors.ListedColormap(list('rg'))
plt.figure(figsize=(8, 8), facecolor='w')
plt.title('original data')
plt.grid(True)
plt.scatter(data[:, 0], data[:, 1], s=30, cmap=cm, edgecolors='none')
plt.show()
for i in range(len(name1)):
    plt.plot(name1[i,0], name1[i,1], 'or')
for i in range(len(name2)):
    plt.plot(name2[i,0], name2[i,1], 'ob')
plt.show() 

3.结果分析

其实通过print的结果可以看出，在迭代了三次之后质心位置就不再发生改变，这是由于数据集样本过少过于简单造成的，但无所谓，远离都是一样的，因此放到我的真的数据集中所跑出的结果和调用API其实是一样的。：

2 3 7 7
2.3333333333333335 3.3333333333333335 7.333333333333333 7.222222222222222
2.7142857142857144 3.5714285714285716 7.625 7.5

聚类结果如下图，可以看出是按照所述原理聚为两类。

4.调用API代码实现

下面是调用python的工具包sklearn中带的K-means写的代码：

#导入工具包
from sklearn.cluster import KMeans
from sklearn import metrics
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import os
#加载数据
def load_data(file_name):
    workspace = 'E:\\study\\dataset\\data_1'
    os.chdir(workspace)
    data = pd.read_csv(file_name)
    return data
#K-means函数
def K_MEANS(data):
	#首先画图看一下原始数据
    plt.scatter(data[:, 0], data[:, 1], marker='o')
    plt.show()
    #枚举法，进行对簇数的确定
    for index, k in enumerate((2, 3, 4, 5)):
        plt.subplot(2, 2, index+1)
        y_pred = KMeans(n_clusters=k, max_iter=100, random_state=9).fit_predict(data)#设置迭代次数为100
        score = metrics.calinski_harabasz_score(data,y_pred)#使用ch值作为评判标准，可以自行了解
        plt.scatter(data[:, 0], data[:, 1], c=y_pred)
    plt.show()#观察聚类结果
#主函数
if __name__ == '__main__':
    _data = load_data('data.csv')
    K_MEANS(_data)

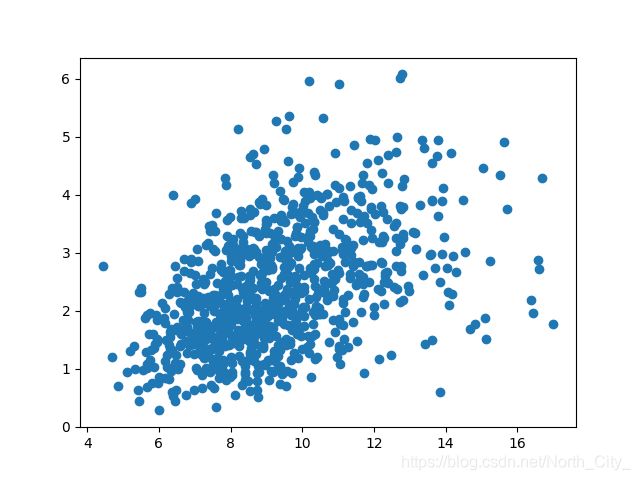
结果显示：
初始数据为：（杂乱无章，并不能肉眼直接可分）

聚类之后：
可以看出对于不同簇数的聚类效果不一样的

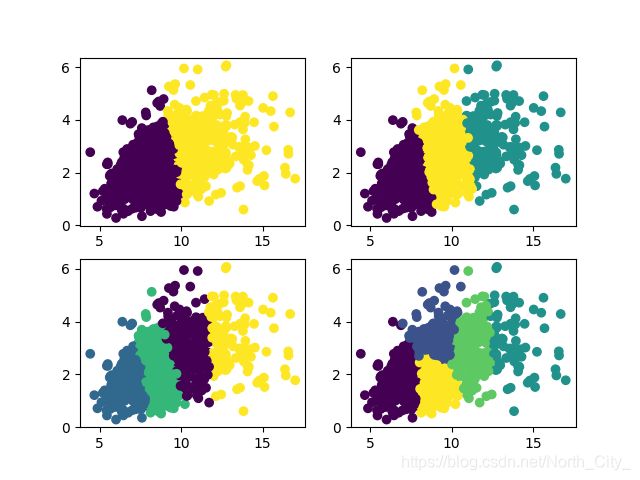
对于调用API跑出的结果，可以试着用自己的程序跑一下，你会发现你的代码其实也可以。

---

总结

感兴趣的同学可以试着自己写一下
祝大家都能写Pythonic，少写Cython