强化学习开发环境搭建与入门实验——CliffWalking与CartPole
文章目录
- 前言
- 环境配置
-
- 创建Conda环境
- 安装Torch
- 安装其他依赖
- gym版本替换(重点)
- 检验
- 服务器特殊配置
-
- 虚拟渲染原理
- 不同来源环境的不同
- Xvfb插件
- 表格型方法
-
- CliffWalking
-
- 程序框架设计
-
- 环境
- 智能体(Agent/Actor)
- 训练方法
- 代码
-
- SARSA
- Q-learning
- 关于Gym库
- 结果可视化
- CartPole
-
- 环境概述
- 状态离散化
- 代码
-
- SARSA
- Q-learning
- 一些结论
-
- 训练速度
- SARSA和Q-learning区别
- 从DQN到Rainbow
-
- 实验过程
- 代码
-
- DQN,DDQN,DuelingDQN代码
- Noisy,Distribution,Rainbow代码
- 实验报告
-
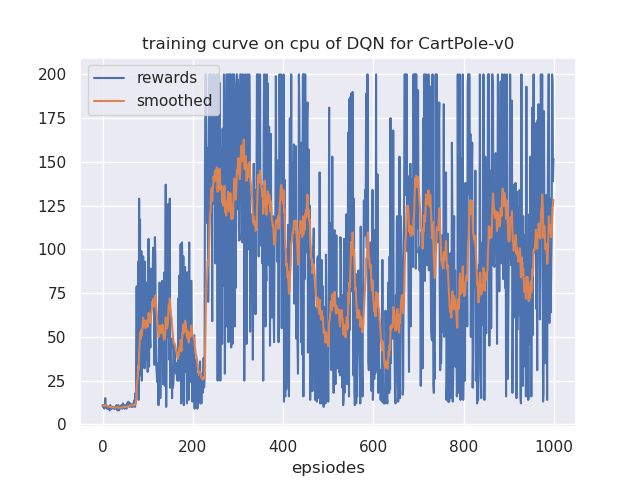
- DQN
- Double DQN(DDQN)
-
- 算法理解
- 结果
- 深度竞争Q网络(dueling DQN)
-
- 算法理解
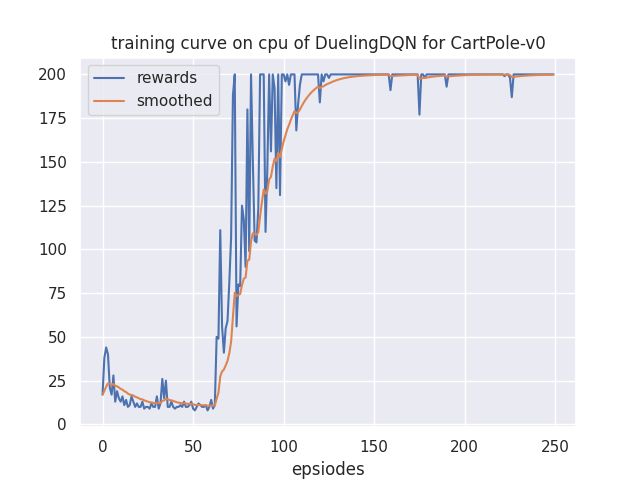
- 初步结果
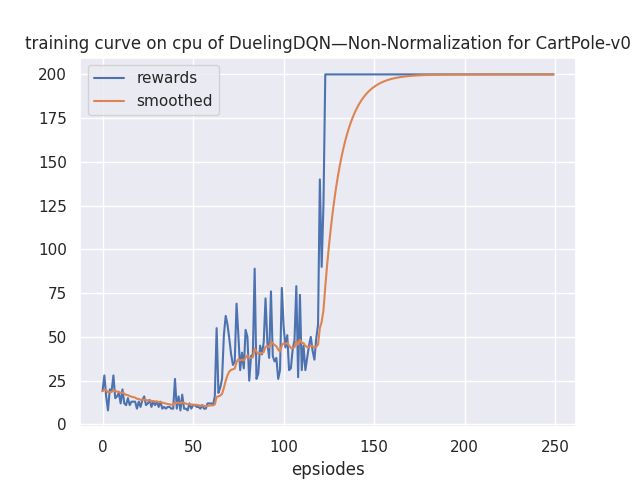
- 退化猜想
- 优先级经验回放(PER,prioritized experience replay)
-
- 算法理解
- 算法实现
- 噪声网络(noisy net)
-
- 算法理解
- 算法实现
- 分布式Q函数(distributed Q-function)
-
- 算法理解
- 区间调参
- 最佳范围
- RainBow
前言
这学期选的强化学习,这课有点阴间的,光是两个小实验,工作量就已经是另一门《人工智能基础》的两倍了,后面的学弟学妹,如果对成绩有追求,但是以前没有过相关经验,慎重选课。
回归正题,首先应该具有两个基础:
这几篇文章内容比较多,conda是一定要看的,服务器的话,如果你目前只打算用本地开发,那这部分可看可不看。
强化学习SARSA与Qlearning
conda虚拟环境解析
有这两个就可以在本地搭建一个不错的环境了,但是,考虑到强化学习训练速度堪忧,所以有必要学习一下云服务器的部署以及远程开发。
linux服务器远程开发
环境配置
到这里就要开始复制easyrl给出的环境了,整体流程和easyrl给出的类似,但是我会做出一些改动,否则完全按照easyrl走下来就会出问题:
easyrl官网
主要依赖:Python 3.7、PyTorch 1.10.0、Gym 0.25.1
创建Conda环境
conda create -n easyrl python=3.7
conda activate easyrl # 激活环境
安装Torch
安装CPU版本:
conda install pytorch==1.10.0 torchvision==0.11.0 torchaudio==0.10.0 cpuonly -c pytorch
安装CUDA版本:
conda install pytorch==1.10.0 torchvision==0.11.0 torchaudio==0.10.0 cudatoolkit=11.3 -c pytorch -c conda-forge
如果安装Torch需要镜像加速的话,点击清华镜像链接,选择对应的操作系统,如win-64,然后复制链接,执行:
conda install pytorch==1.10.0 torchvision==0.11.0 torchaudio==0.10.0 cudatoolkit=11.3 -c https://mirrors.tuna.tsinghua.edu.cn/anaconda/cloud/pytorch/win-64/
也可以使用PiP镜像安装(仅限CUDA版本):
pip install torch==1.10.0+cu113 torchvision==0.11.0+cu113 torchaudio==0.10.0 --extra-index-url https://download.pytorch.org/whl/cu113
安装其他依赖
在project目录下执行:
pip install -r requirements.txt
gym版本替换(重点)
虚拟环境最初是按照easyrl官网给的环境配置的,但是发现在import gym的时候出现了属性缺失的bug,那十有八九是版本本身的问题了,我起初怀疑是linux和windows的区别导致的,然而我在windows本地确认了一下,也出现了import问题,那确实是版本问题。
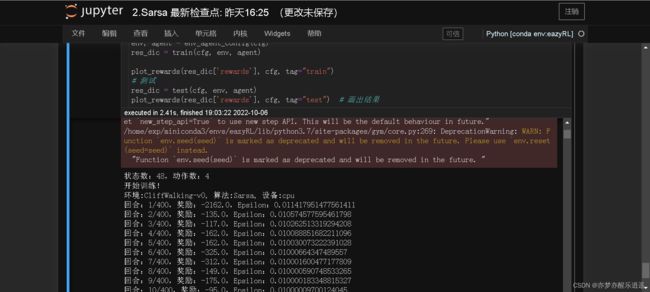
于是我就开始测试gym版本,首先卸掉0.21.0的gym,直接安装最新适配版,是一个0.26的,然后我又跑了一下easyrl给的示例代码,结果导包没问题,最后又有了找不到env.seed函数的bug,这应该是代码和版本不兼容,十有八九是seed函数被deprecated了(变成了reset函数)。
结果就从0.22,0.23,0.24逐渐测试,终于在0.24跑通了easyrl项目里的Q-learning,SARSA的示例代码,同时也得到了一串意料之中的提示,为了更好的适配,后面我又换成了0.25.1版本:
pip uninstall gym
pip install gym==0.25.1
检验
先检验一下torch和cuda(可选)
CPU版本Torch请忽略此步,执行如下Python脚本,如果返回True说明CUDA版本安装成功:
import torch
print(torch.cuda.is_available())
然后检验一下代码是否可以运行,找到sarsa的notebook,进去以后,切换环境(requerement里面有ipykernel,所以可以直接在notebook里切换)
重启并运行所有,可以看到一堆警告+好的结果。之所以有警告,是因为easyrl的代码都是老版本的写法,0.25.1能兼容就很不错了,0.26.1干脆就跑不了。
服务器特殊配置
本地跑的朋友可以跳过了。
虚拟渲染原理
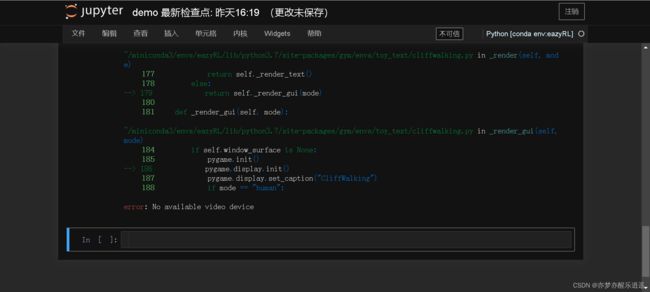
如果你在服务器端使用render函数,就会报错。
这是因为,render函数要锁定电脑的显示设备,然后把他渲染好的图像逐帧丢进去,形成动画。
但是如果你用的是服务器,或者虚拟机,他本身是没有显示设备的,这才会报错。
那么,如何实现把在本地jupyter notebook上显示服务器的render信息呢?
核心原理是在服务器进行虚拟渲染,然后将渲染后的rgb矩阵发送到本地,在本地使用matplotlib输出一张图片,并且不断刷新,形成动画。
给出实例代码:
#env=gym.make('CliffWalking-v0',render_mode='rgb_array')
env=gym.make('CartPole-v0',render_mode='rgb_array') # 声明这个环境要用rgb_array模式渲染,每次render返回一个矩阵
#env=gym.make('MountainCar-v0',render_mode='rgb_array')
#env=gym.make('Acrobot-v1',render_mode='rgb_array')
#env=gym.make('FrozenLake-v1',render_mode='rgb_array')
env.reset()
img=plt.imshow(env.render()[0]) # 每次返回一个(1,400,600,3)维度的数组,需要把第一维取出才能正常显示
for _ in range(1000):
action=env.action_space.sample() # action走一步
env.step(action)
data=env.render()
img.set_data(data[0]) # 刷新图片
display.display(plt.gcf())
display.clear_output(wait=True)
env.close()
不同来源环境的不同
在这个代码中,我用5个环境去测试服务器虚拟渲染。这5个环境有两个来源,我找到了gym的环境目录,如果你逐个去看,就可以看到CliffWalking和FrozenLake是toy_text里的,其他三个是classic_control里的:
如果你用CartPole那一批,就可以直接进行渲染:
但是如果你切换成了CliffWalking那一批,就会报错,没有可用显示设备
Xvfb插件
对于报错的那一批环境,就需要用Xvfb插件辅助了。
Xvfb全称X Windows Virtual Frame Buffer (Xvfb) ,从名字来看,是一个虚拟渲染框架插件,有很多包都需要Xvfb依赖。比如我们这个gym。
su root
yum install Xvfb
注意X是大写,fb不要写成bf。把这个包安装以后,重新运行jupyter notebook(可以叠加nuhup命令挂起):
xvfb-run -s "-screen 0 1400x900x24" jupyter notebook
这里的x是小写,中间那个参数我也不太明白,应该是确定图像大小的。
启动插件以后,再次运行代码,就可以得到预期的结果:
表格型方法
CliffWalking
程序框架设计
环境
gym.make可以给出一个现成的环境
环境已经有了,所以我们只需要给出Agent类,给出训练episode和测试episode的函数,以及一个主函数即可。
智能体(Agent/Actor)
Agent类包括:
- Q表格(Agent的参数),以及其他训练参数。
- epsilon-greedy方法(sample方法)
- 目标策略方法(predice方法)
- 更新Q表格的方法(learn方法)
训练方法
run_episode方法是区分SARSA和Q-learning的关键。
首先初始化observation和action,之后开始循环,直到一个回合结束break。
SARSA循环中,是先获取下一步的obs和action,再进行优化
Q-learning中,只需要获取下一步的obs就直接按照目标策略优化,但是选取下一步的action时还是按照epsilon-greedy的行为策略选取的,这就是所谓的目标策略与行为策略分离,目标策略在总体上把控方向,行为策略则保留了一定的不确定性。
代码
SARSA
先给出SARSA版本的完全版代码
#!/usr/bin/env python
# -*- coding:utf-8 -*-
import time
import numpy as np
import gym
class SarsaAgent(object):
def __init__(self, obs_n, act_n, learning_rate=0.01, gamma=0.9, e_greedy=0.1):
self.act_n = act_n # 动作的维度, 有几个动作可选
self.lr = learning_rate # 学习率
self.gamma = gamma # 折扣因子,reward的衰减率
self.epsilon = e_greedy # 按一定的概率随机选动作
self.Q = np.zeros((obs_n, act_n)) # 创建一个Q表格
# 根据输入观察值(这个代码不区分state和observation),采样输出的动作值
def sample(self, obs):
if np.random.uniform(0, 1) < (1.0 - self.epsilon): # 根据table的Q值选动作
action = self.predict(obs) # 调用函数获得要在该观察值(或状态)条件下要执行的动作
else:
action = np.random.choice(self.act_n) # e_greedy概率直接从动作空间中随机选取一个动作
return action
# 根据输入的观察值,预测输出的动作值
def predict(self, obs):
Q_list = self.Q[obs, :] # 从Q表中选取状态(或观察值)对应的那一行
maxQ = np.max(Q_list) # 获取这一行最大的Q值,可能出现多个相同的最大值
action_list = np.where(Q_list == maxQ)[0] # np.where(条件)功能是筛选出满足条件的元素的坐标
action = np.random.choice(action_list) # 这里尤其如果最大值出现了多次,随机取一个最大值对应的动作就成
return action
# 给环境作用一个动作后,对环境的所有反馈进行学习,也就是用环境反馈的结果来更新Q-table
def learn(self, obs, action, reward, next_obs, next_action, done):
"""
on-policy
obs:交互前的obs, 这里observation和state通用,也就是公式或者伪代码码中的s_t
action: 本次交互选择的动作, 也就是公式或者伪代码中的a_t
reward: 本次与环境交互后的奖励, 也就是公式或者伪代码中的r
next_obs: 本次交互环境返回的下一个状态,也就是s_t+1
next_action: 根据当前的Q表,针对next_obs会选择的动作,a_t+1
done: 回合episode是否结束
"""
predict_Q = self.Q[obs, action]
if done:
target_Q = reward # 如果到达终止状态, 没有下一个状态了,直接把奖励赋值给target_Q
else:
target_Q = reward + self.gamma * self.Q[next_obs, next_action] # 这两行代码直接看伪代码或者公式
self.Q[obs, action] = predict_Q + self.lr * (target_Q - predict_Q) # 修正q
def run_episode(env, agent, render=False):
total_steps = 0 # 记录每一个回合episode走了多少step
total_reward = 0 # 记录一个episode获得总奖励
obs = env.reset() # 重置环境,重新开始新的一轮(episode)
action = agent.sample(obs) # 根据算法选择一个动作,采用ε-贪婪算法选取动作
while True:
next_obs, reward, done, info = env.step(action) # 与环境进行一次交互,即把动作action作用到环境,并得到环境的反馈
next_action = agent.sample(next_obs) # 根据获得的下一个状态,执行ε-贪婪算法后,获得下一个动作
# 训练Sarsa算法, 更新Q表格
agent.learn(obs, action, reward, next_obs, next_action, done)
action = next_action
obs = next_obs # 存储上一个观测值(这里状态和观测不区分,正常observation是state的一部分)
total_reward += reward
total_steps += 1
if render:
env.render() # 重新画一份效果图
if done: # 如果达到了终止状态,则回合结束,跳出该轮循环
break
return total_reward, total_steps
def test_episode(env, agent):
total_reward = 0
obs = env.reset()
while True:
action = agent.predict(obs) # greedy
next_obs, reward, done, info = env.step(action)
total_reward += reward
obs = next_obs
time.sleep(0.1)
env.render()
if done:
break
return total_reward
def main():
env = gym.make("CliffWalking-v0") # 悬崖边行走游戏,动作空间及其表示为:0 up , 1 right, 2 down, 3 left
agent = SarsaAgent(
obs_n=env.observation_space.n,
act_n=env.action_space.n,
learning_rate=0.1,
gamma=0.9,
e_greedy=0.1)
is_render = False
for episode in range(500):
ep_reward, ep_steps = run_episode(env, agent, is_render)
print('Episode %s: steps = %s, reward = %.lf' % (episode, ep_steps, ep_reward))
# 每隔20个episode渲染一下看看效果
if episode % 20 == 0:
is_render = True
else:
is_render = False
# 训练结束,查看算法效果
for episode in range(10):
total_reward=test_episode(env, agent)
print('test %d reward = %.lf' % (episode,total_reward))
if __name__ == '__main__':
main()
Q-learning
Q-learning就是简单修改一下episode就可以:
def run_episode(env, agent, render=False):
total_steps = 0 # 记录每一个回合episode走了多少step
total_reward = 0 # 记录一个episode获得总奖励
obs = env.reset() # 重置环境,重新开始新的一轮(episode)
action = agent.sample(obs) # 根据算法选择一个动作,采用ε-贪婪算法选取动作
while True:
next_obs, reward, done, info = env.step(action) # 与环境进行一次交互,即把动作action作用到环境,并得到环境的反馈
# 训练Q-learning算法, 以目标策略更新Q表格
agent.learn(obs, action, reward, next_obs, agent.predict(next_obs), done)
# 实际的行为策略
action = agent.sample(next_obs)
obs = next_obs # 存储上一个观测值(这里状态和观测不区分,正常observation是state的一部分)
total_reward += reward
total_steps += 1
if render:# 重新画一份效果图
env.render()
if done: # 如果达到了终止状态,则回合结束,跳出该轮循环
break
return total_reward, total_steps
关于Gym库
上面的代码主要用的就是gym库,这里对其中的一些接口进行解释。
不同版本的gym还是有一些差别的,比如一些函数的用法,以及项目的结构。但是该有的东西肯定是都有的,出bug只是是代码和包版本不匹配,改一改代码就能用了。
Gym负责提供env以及相关的可视化。
首先通过make方法获取一个env,这是最原始的环境。Env可以采用Wapper进行自定义封装,不过这是后话了,最开始是有一个默认的封装的。
给定一个env,有若干接口:reset,step(action),render。
- reset。负责初始化状态,曾经是用seed函数,0.25以后都用reset了。
- step。其实环境无非就是接受一个action,然后给反馈,step方法是环境的核心,输入action,返回下一个观察(内含state信息),奖赏,以及其他信息等。
- render。这是负责可视化的,会在屏幕上输出图像。初学者会用这个,后面就不会用了,因为训练的过程实在是枯燥无味,更多的是用episode-reward曲线图去可视化整体的过程,不回去关注具体某一个回合训练的怎么样的。
结果可视化
- 结果采用matplotlib绘制训练过程的episode-reward曲线(代码里没写,不过网上很多)
- 结合render方法每隔一定episode就展示一次当前训练的情况(远程服务器需要另做修改)
- 最后训练完毕后,对模型进行多次采样(test_episode),维持动画,反复展示最佳训练结果(可以适当加入time暂停,将动画速度放慢)。
CartPole
环境概述
CartPole是一个新的环境,第一步需要了解环境的基本情况,即Action和Observation
Action只有两个:分别是左移右移(0,1)
Observation 是四元组:
CartPole的观测状态空间是4维连续的,这里给出上下限:
High: [4.8000002e+00 3.4028235e+38 4.1887903e-01 3.4028235e+38]
Low: [-4.8000002e+00 -3.4028235e+38 -4.1887903e-01 -3.4028235e+38]
可以看出,状态空间很大,所以假设第二个状态与第四个状态都在-3到3之间,因为现实中也不能允许速度太大(可以当做超参数调节),其次,因为是连续的,所以要仔细考虑一下Q表格如何构建,因为Q表格是离散的。
状态离散化
假设以0.1精度为分割,那么大概有370w种状态,还是可以接受的,放在服务器上跑个半小时也出来了。
而且精度还可以修改,适应电脑本身的情况,比如精度为0的时候(整数),训练速度会显著提升。
从具体的实现来看,需要根据上下限,基于精度构建一个等间距的分割向量(get_distribution_arr方法),向量中的每一个值都是一个吸引子,负责把周围邻域中的数值吸附到这个值上。比如精度为0.1的时候,(0.05,0.15)都会变成0.1,又比如精度为1的时候,(0.5,1.5)之间的都会变成1。
Q表格使用字典方式储存,key就是区间分割值取一定精度后的字符串。如果后面新来一个obs,可以直接把值限定在范围内后,取精度,可以直接对应到state向量中(代码中的实现方法为obs2state)
由上,实现了连续状态空间的离散化。
在空间离散化后,训练流程和CliffWalking是一模一样的。
代码
SARSA
import gym
import numpy as np
import matplotlib.pyplot as plt
import time
class SarsaAgent(object):
def __init__(self, env, learning_rate=0.01, gamma=0.9, e_greedy=0.1, round_num=0):
self.lr = learning_rate # 学习率
self.gamma = gamma # 折扣因子,reward的衰减率
self.epsilon = e_greedy # 按一定的概率随机选动作
self.round_num=round_num # 精度
self.action_num = list(range(env.action_space.n))
self.low0, self.low2 = np.round(np.take(env.observation_space.low, [0, 2]), self.round_num)
self.high0, self.high2 = np.round(np.take(env.observation_space.high, [0, 2]), self.round_num)
self.Q = self.init_QTable() # 创建一个Q表格
# 根据范围+精度划分区间
def get_distrubution_arr(self,low,high,round_num):
cnt=int((high-low)*(10**round_num)+1)
a=np.round(np.linspace(low,high,cnt),round_num)
if not np.sum(0==a):# 修正
a=np.concatenate([a,np.array([-0.,0.])])
else:
a=np.concatenate([a,np.array([-0.])])
return a
def init_QTable(self):
a = self.get_distrubution_arr(self.low0, self.high0, self.round_num)
b = self.get_distrubution_arr(-3., 3., self.round_num)
c = self.get_distrubution_arr(self.low2, self.high2, self.round_num)
d = self.get_distrubution_arr(-3., 3., self.round_num)
Q_dict = dict()
for s1 in a:
for s2 in b:
for s3 in c:
for s4 in d:
Q_dict[str(np.round(np.array([s1, s2, s3, s4]), self.round_num))] =\
np.random.uniform(0, 1, len(self.action_num))
print('len(Q_dict) = ', len(Q_dict))
return Q_dict
# 将连续动作obs离散化为state,对应Q表行
def obs2state(self, obs):
if type(obs) == str:
print('obs already str')
return obs
s1, s2, s3, s4 = np.round(obs, self.round_num)
s1 = np.clip(s1, -4.8, 4.8)
s2 = np.clip(s3, -3., 3.)
s3 = np.clip(s2, -0.4, 0.4)
s4 = np.clip(s4, -3., 3.)
return str(np.round(np.array([s1, s2, s3, s4]), self.round_num))
# 根据输入obs,采样输出的动作值,先进行一步离散化
def sample(self, obs):
state=self.obs2state(obs) # 离散化
if np.random.uniform(0, 1) < (1.0 - self.epsilon): # 根据table的Q值选动作
action = self.predict(state) # 调用函数获得要在该观察值(或状态)条件下要执行的动作
else:
action = np.random.choice(self.action_num) # e_greedy概率直接从动作空间中随机选取一个动作
return action # 0/1
# 根据输入的观察值,预测输出的动作值
def predict(self, state):
Q_list = self.Q[state] # 从Q表中选取状态(或观察值)对应的那一行
maxQ = np.max(Q_list) # 获取这一行最大的Q值,可能出现多个相同的最大值
action_list = np.where(Q_list == maxQ)[0] # np.where(条件)功能是筛选出满足条件的元素的坐标
action = np.random.choice(action_list) # 这里尤其如果最大值出现了多次,随机取一个最大值对应的动作就成
return action
# 给环境作用一个动作后,对环境的所有反馈进行学习,也就是用环境反馈的结果来更新Q-table
def learn(self, obs, action, reward, next_obs, next_action, done):
state=self.obs2state(obs) # 离散化
next_state=self.obs2state(next_obs)
predict_Q = self.Q[state][action]
# 优化
if done:
target_Q = reward # 如果到达终止状态, 没有下一个状态了,直接把奖励赋值给target_Q
else:
target_Q = reward + self.gamma * self.Q[next_state][next_action] # 这两行代码直接看伪代码或者公式
self.Q[state][action] = predict_Q + self.lr * (target_Q - predict_Q) # 修正q
def run_episode(env, agent, render=False):
total_steps = 0 # 记录每一个回合episode走了多少step
total_reward = 0 # 记录一个episode获得总奖励
obs = env.reset() # 重置环境,重新开始新的一轮(episode)
action = agent.sample(obs) # 根据算法选择一个动作,采用ε-贪婪算法选取动作
while True:
next_obs, reward, done, info = env.step(action) # 与环境进行一次交互,即把动作action作用到环境,并得到环境的反馈
next_action = agent.sample(next_obs) # 根据获得的下一个状态,执行ε-贪婪算法后,获得下一个动作
# 训练Sarsa算法, 更新Q表格,注意
agent.learn(obs, action, reward, next_obs, next_action, done)
action = next_action
obs = next_obs # 存储上一个观测值(这里状态和观测不区分,正常observation是state的一部分)
total_reward += reward
total_steps += 1
if render:
env.render() # 重新画一份效果图
if done: # 如果达到了终止状态,则回合结束,跳出该轮循环
break
return total_reward, total_steps
def test_episode(env, agent):
total_reward = 0
obs = env.reset()
while True:
action = agent.predict(agent.obs2state(obs)) # greedy
next_obs, reward, done, info = env.step(action)
total_reward += reward
obs = next_obs
#time.sleep(0.1)
env.render()
if done:
break
return total_reward
def main():
env = gym.make('CartPole-v0')
agent = SarsaAgent(
env,
learning_rate=0.1,
gamma=0.9,
e_greedy=0.1,
round_num=0)
is_render = False
for episode in range(1000):
ep_reward, ep_steps = run_episode(env, agent, is_render)
print('Episode %s: steps = %s, reward = %.lf' % (episode, ep_steps, ep_reward))
# 每隔20个episode渲染一下看看效果
if episode % 50 == 0:
is_render = True
else:
is_render = False
# 训练结束,查看算法效果
for episode in range(10):
total_reward=test_episode(env, agent)
print('test %d reward = %.lf' % (episode,total_reward))
if __name__ == '__main__':
main()
Q-learning
同样是改一下episode
def run_episode(env, agent, render=False):
total_steps = 0 # 记录每一个回合episode走了多少step
total_reward = 0 # 记录一个episode获得总奖励
obs = env.reset() # 重置环境,重新开始新的一轮(episode)
action = agent.sample(obs) # 根据算法选择一个动作,采用ε-贪婪算法选取动作
while True:
next_obs, reward, done, info = env.step(action) # 与环境进行一次交互,即把动作action作用到环境,并得到环境的反馈
# 训练Q-learning算法, 以目标策略更新Q表格
agent.learn(obs, action, reward, next_obs, agent.predict(agent.obs2state(next_obs)), done)
# 实际的行为策略
action = agent.sample(next_obs)
obs = next_obs # 存储上一个观测值(这里状态和观测不区分,正常observation是state的一部分)
total_reward += reward
total_steps += 1
if render:
env.render() # 重新画一份效果图
if done: # 如果达到了终止状态,则回合结束,跳出该轮循环
break
return total_reward, total_steps
一些结论
训练速度
CliffWalking的训练中,刚开始一个episode时间特别长,这是因为策略不够好,迟迟到不了终点,不能获得done状态,就会一直迭代。到了后面,episode时间会缩短,因为策略越来越趋向于稳定,每次的路线也会固定下来。
CartPole是反过来的,因为他是以坚持的时间长度为reward的,所以刚开始时间很短,后面逐渐加长到200的上限。
本质上,这两种变化都是一样的,反映了策略向着最佳方向的转变。
SARSA和Q-learning区别
如果单纯论收益的话,Q-learning是强于SARSA的,但是稳定性安全性上,SARSA更强。就像我们平时在山上走,人是不会为了赶路快而贴着悬崖走的。
从效果上来说,Sarsa更胆小,Q-learning更激进。比如悬崖问题,t时刻你在s1,然后采取了down行为,走到了s2,这个时候Q-learning和Sarsa就有分歧了:
- Q-learning的目标策略认为在S2时刻,你一定会向右走,所以直接把Q值更新,很有可能是一个增大的Q值,因为距离终点更近。虽然实际上因为 ϵ − g r e e d y \epsilon-greedy ϵ−greedy可能走到悬崖里,但是已经和悬崖边的S1-down的Q值没有关系了,你走到悬崖边里只会让S2的Q值变小。当你下次走到S1的时候,S1-down的Q值仍然很大,S1仍然也会选择down策略。
- Sarsa不放心实际策略的执行,所以等S2选择了Action后才会更新S1的Q值。如果是S2-down,即S2的Q值很小,这就会导致S1-down的Q值变小,下一次走到S1的时候,很有可能就不会选择down策略了。
- 随着时间推进,Sarsa和Q-learning两种方法的优化效果会逐渐趋同,但是前期累积的差异已经无法扳回了
总的来说,Q-learning有一种不见棺材不掉泪的感觉,目标策略只负责大方向,不会过多约束行为策略,非得行为策略一步走到陷阱才会改进上一步的Q值(目标策略),但是Sarsa只要走到陷阱的附近就会改进上一步的Q值,甚至会有一种传递性(这也是图中Sarsa为什么要走最外面而不是中间层的原因),即Q-learning更加大胆,Sarsa比较胆小。
你可能觉得Sarsa不如Q-learning,但是实际上Sarsa是对Q-learning的改进,很多对安全性要求高的任务中,即使是牺牲一些效率也要保证安全,这就要用Sarsa,但是另一些任务,即使是发生失误也无所谓,就要极致的速度,那就用Q-learning。
从DQN到Rainbow
实验过程
老师让我们用Rainbow去玩Atari游戏,这个任务的难度很大,雅达利环境的安装就是一个问题,下面这篇文章给出了几种解决方法。我的建议是,新建一个环境,用gym0.19的老版本去安装atari游戏,这是最省事的办法。
Atari安装
最开始,我打算先用DQN把雅达利写出来,然后再把RainBow叠加到框架中。
但是经过测试,发现计算机硬件太差会导致雅达利的学习效果太差,无法得到有效结果,所以只能选择CartPole作为游戏目标。实现了全部的算法。
代码
DQN,DDQN,DuelingDQN代码
这个代码是从easyRL的代码库里弄出来的,他们的代码库写的比较分散,所以前期的拼接工作比较麻烦,我这里已经拼好了。
看起来很长,实际上部件分的比较清晰,不用担心。
这一份代码可以实现DQN,DDQN,DuelingDQN三种算法。DDQN只需要改一下predict函数即可。DuelingDQN只需要把model从MLP替换成DuelingMLP即可。
import sys
import os
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
import torchvision.transforms as transforms
#curr_path = os.path.dirname(os.path.abspath(__file__)) # 当前文件所在绝对路径
curr_path=os.getcwd()
parent_path = os.path.dirname(curr_path) # 父路径
sys.path.append(parent_path) # 添加路径到系统路径
import gym
import torch
import datetime
import numpy as np
import math
import random
import os
import numpy as np
from pathlib import Path
import matplotlib.pyplot as plt
import seaborn as sns
import json
import pandas as pd
from matplotlib.font_manager import FontProperties # 导入字体模块
'''
from common.utils import save_results_1, make_dir
from common.utils import plot_rewards
'''
curr_time = datetime.datetime.now().strftime("%Y%m%d-%H%M%S") # 获取当前时间
def make_dir(*paths):
''' 创建文件夹
'''
for path in paths:
Path(path).mkdir(parents=True, exist_ok=True)
def save_results(res_dic, tag='train', path = None):
''' 保存奖励
'''
Path(path).mkdir(parents=True, exist_ok=True)
df = pd.DataFrame(res_dic)
df.to_csv(f"{path}/{tag}ing_results.csv",index=None)
print('Results saved!')
def smooth(data, weight=0.9):
'''用于平滑曲线,类似于Tensorboard中的smooth
Args:
data (List):输入数据
weight (Float): 平滑权重,处于0-1之间,数值越高说明越平滑,一般取0.9
Returns:
smoothed (List): 平滑后的数据
'''
last = data[0] # First value in the plot (first timestep)
smoothed = list()
for point in data:
smoothed_val = last * weight + (1 - weight) * point # 计算平滑值
smoothed.append(smoothed_val)
last = smoothed_val
return smoothed
def plot_rewards(rewards,cfg,path=None,tag='train'):
sns.set()
plt.figure() # 创建一个图形实例,方便同时多画几个图
plt.title(f"{tag}ing curve on {cfg.device} of {cfg.algo_name} for {cfg.env_name}")
plt.xlabel('epsiodes')
plt.plot(rewards, label='rewards')
plt.plot(smooth(rewards), label='smoothed')
plt.legend()
if cfg.save_fig:
plt.savefig(f"{path}/{tag}ing_curve.png")
if cfg.show_fig:
plt.show()
class Config:
'''超参数
'''
def __init__(self):
############################### hyperparameters ################################
self.algo_name = 'DuelingDQN—Non-Normalization' # algorithm name
self.env_name = 'CartPole-v0' # environment name
self.device = torch.device(
"cuda" if torch.cuda.is_available() else "cpu") # check GPU
self.seed = 10 # 随机种子,置0则不设置随机种子
self.train_eps = 250 # 训练的回合数
self.test_eps = 20 # 测试的回合数
################################################################################
################################## 算法超参数 ###################################
self.gamma = 0.95 # 强化学习中的折扣因子
self.epsilon_start = 0.90 # e-greedy策略中初始epsilon
self.epsilon_end = 0.01 # e-greedy策略中的终止epsilon
self.epsilon_decay = 500 # e-greedy策略中epsilon的衰减率
self.lr = 0.0001 # 学习率
self.memory_capacity = 100000 # 经验回放的容量
self.batch_size = 64 # mini-batch SGD中的批量大小
self.target_update = 4 # 目标网络的更新频率
self.hidden_dim = 256 # 网络隐藏层
################################################################################
################################# 保存结果相关参数 ################################
self.result_path = curr_path + "/outputs/" + self.env_name + \
'/' + curr_time + '/results/' # 保存结果的路径
self.model_path = curr_path + "/outputs/" + self.env_name + \
'/' + curr_time + '/models/' # 保存模型的路径
self.save_fig = True # 是否保存图片
self.show_fig = True
self.print_res_epi = 20 # 输出结果的频率
################################################################################
class MLP(nn.Module):
def __init__(self, n_states,n_actions,hidden_dim=128):
""" 初始化q网络,为全连接网络
n_states: 输入的特征数即环境的状态维度
n_actions: 输出的动作维度
"""
super(MLP, self).__init__()
self.fc1 = nn.Linear(n_states, hidden_dim) # 输入层
self.fc2 = nn.Linear(hidden_dim,hidden_dim) # 隐藏层
self.fc3 = nn.Linear(hidden_dim, n_actions) # 输出层
def forward(self, x):
# 各层对应的激活函数
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
return self.fc3(x)
class DuelingMLP(nn.Module):
def __init__(self,n_states,n_actions,hidden_dim=128):
super(DuelingMLP,self).__init__()
# 隐藏层
self.hidden = nn.Sequential(
nn.Linear(n_states, hidden_dim),
nn.ReLU()
)
# 优势函数
self.advantage = nn.Sequential(
nn.Linear(hidden_dim, hidden_dim),
nn.ReLU(),
nn.Linear(hidden_dim, n_actions)
)
# 价值函数
self.value = nn.Sequential(
nn.Linear(hidden_dim, hidden_dim),
nn.ReLU(),
nn.Linear(hidden_dim, 1)
)
def forward(self, x):
x = self.hidden(x)
advantage = self.advantage(x)
value = self.value(x)
return value + (advantage - advantage.mean())# A函数归一化
#print(value)
#return value + advantage# 不归一化
class ReplayBuffer:
def __init__(self, capacity):
self.capacity = capacity # 经验回放的容量
self.buffer = [] # 缓冲区
self.position = 0
def push(self, state, action, reward, next_state, done):
''' 缓冲区是一个队列,容量超出时去掉开始存入的转移(transition)
'''
if len(self.buffer) < self.capacity: # 在达到capacity之前,不断扩充列表长度,直到长度达到上限。
self.buffer.append(None) #这个是有用的,如果长度不够batch_size就不更新
self.buffer[self.position] = (state, action, reward, next_state, done)
self.position = (self.position + 1) % self.capacity
def sample(self, batch_size):
batch = random.sample(self.buffer, batch_size) # 随机采出小批量转移
state, action, reward, next_state, done = zip(*batch) # 解压成状态,动作等
return state, action, reward, next_state, done # 返回的都是一个batch_size长度的一维序列(可能嵌套,因为state通常是多维的)
def __len__(self):
''' 返回当前存储的量
'''
return len(self.buffer)
class DQN:
def __init__(self,n_actions,model,memory,cfg):
self.n_actions = n_actions
self.device = torch.device(cfg.device) # cpu or cuda
self.gamma = cfg.gamma # 奖励的折扣因子
# e-greedy策略相关参数
self.sample_count = 0 # 用于epsilon的衰减计数
self.epsilon = lambda sample_count: cfg.epsilon_end + \
(cfg.epsilon_start - cfg.epsilon_end) * \
math.exp(-1. * sample_count / cfg.epsilon_decay)
self.batch_size = cfg.batch_size
self.policy_net = model.to(self.device) # 复制两个网络到指定设备
self.target_net = model.to(self.device)
for target_param, param in zip(self.target_net.parameters(),self.policy_net.parameters()): # 逐层复制参数到目标网路targe_net
target_param.data.copy_(param.data)
self.optimizer = optim.Adam(self.policy_net.parameters(), lr=cfg.lr) # 优化器
self.memory = memory # 经验回放
def sample(self, state):
'''
'''
self.sample_count += 1
action = self.predict(state) if random.random() > self.epsilon(self.sample_count) else random.randrange(self.n_actions)
return action
def predict(self,state): # 完全可以插入sample函数中
'''贪婪法则选取q最大动作
通过一个state选择一个action
函数仅针对一个state编写,但是会照顾state维度(unsqueeze),否则无法进行批量操作。
'''
with torch.no_grad():
state = torch.tensor(state, device=self.device, dtype=torch.float32).unsqueeze(dim=0) # 插入维度,让state在列维度
#print(state.shape) # [1,4]
q_values = self.policy_net(state) # DDQN
#q_values=self.target_net(state) # 普通DQN
#print(q_values) # [1,2]
action = q_values.max(1)[1].item() # max函数返回最大值与indice,所以取[1]为选择Q值最大的动作,得到action列向量
return action
def update(self):
if len(self.memory) < self.batch_size: # 当memory中不满足一个批量时,不更新策略
return
# 从经验回放中(replay memory)中随机采样一个批量的转移(transition)
state_batch, action_batch, reward_batch, next_state_batch, done_batch = self.memory.sample(
self.batch_size)
state_batch = torch.tensor(np.array(state_batch), device=self.device, dtype=torch.float) # list转tensor,初步维度处理
action_batch = torch.tensor(action_batch, device=self.device).unsqueeze(1) # unsqueeze转列向量
reward_batch = torch.tensor(reward_batch, device=self.device, dtype=torch.float)
next_state_batch = torch.tensor(np.array(next_state_batch), device=self.device, dtype=torch.float)
done_batch = torch.tensor(np.float32(done_batch), device=self.device)
q_values = self.policy_net(state_batch).gather(dim=1, index=action_batch) # 计算当前状态(s_t,a)对应的Q(s_t, a)
next_q_values = self.target_net(next_state_batch).max(1)[0].detach() # detach冻结目标网络梯度,计算下一时刻的状态(s_t_,a)对应的Q值
#print(q_values.shape,next_q_values.shape) # q value是列向量,但是next_q_values是一维不定形。torch.Size([64, 1]) torch.Size([64])
# 计算期望的Q值,对于终止状态,此时done_batch[0]=1, 对应的expected_q_value等于reward
expected_q_values = reward_batch + self.gamma * next_q_values * (1-done_batch)
loss = nn.MSELoss()(q_values, expected_q_values.unsqueeze(1)) # 计算均方根损失,done,reward,next_q都是一维向量,结果需要unsqueeze
# 优化更新模型
self.optimizer.zero_grad()
loss.backward()
for param in self.policy_net.parameters(): # clip防止梯度爆炸
param.grad.data.clamp_(-1, 1)
self.optimizer.step()
def save(self, path): # 保存目标网络
torch.save(self.target_net.state_dict(), path+'checkpoint.pth')
def load(self, path):
self.target_net.load_state_dict(torch.load(path+'checkpoint.pth'))
for target_param, param in zip(self.target_net.parameters(), self.policy_net.parameters()):
param.data.copy_(target_param.data)
def env_agent_config(cfg):
''' 创建环境和智能体
'''
env = gym.make(cfg.env_name) # 创建环境
n_states = env.observation_space.shape[0] # 状态维度
n_actions = env.action_space.n # 动作维度
print(f"n states: {n_states}, n actions: {n_actions}")
#model = MLP(n_states,n_actions)
model=DuelingMLP(n_states,n_actions)
memory = ReplayBuffer(cfg.memory_capacity)
agent = DQN(n_actions, model, memory, cfg) # 创建智能体
if cfg.seed !=0: # 设置随机种子
torch.manual_seed(cfg.seed)
env.seed(cfg.seed)
np.random.seed(cfg.seed)
return env, agent
def train(cfg, env, agent):
''' 训练
'''
print('开始训练!')
print(f'环境:{cfg.env_name}, 算法:{cfg.algo_name}, 设备:{cfg.device}')
rewards = [] # 记录所有回合的奖励
steps = []
for i_ep in range(cfg.train_eps):
ep_reward = 0 # 记录一回合内的奖励
ep_step = 0
state = env.reset() # 重置环境,返回初始状态
while True:
ep_step += 1
action = agent.sample(state) # 选择动作
next_state, reward, done, _ = env.step(action) # 更新环境,返回transition
agent.memory.push(state, action, reward,
next_state, done) # 保存transition
state = next_state # 更新下一个状态
agent.update() # 更新智能体
ep_reward += reward # 累加奖励
if done:
break
if (i_ep + 1) % cfg.target_update == 0: # 智能体目标网络更新
agent.target_net.load_state_dict(agent.policy_net.state_dict())
steps.append(ep_step)
rewards.append(ep_reward)
if (i_ep + 1) % cfg.print_res_epi == 0:
#print(agent.policy_net(torch.Tensor(state)))
print(f'Episode:{i_ep+1}/{cfg.train_eps}, Reward:{ep_reward:.2f}, Step:{ep_step:.2f} Epislon:{agent.epsilon(agent.sample_count):.3f}')
print('Finish training!')
env.close()
res_dic = {'rewards':rewards,'steps':steps}
return res_dic
def test(cfg, env, agent):
print('开始测试!')
print(f'环境:{cfg.env_name}, 算法:{cfg.algo_name}, 设备:{cfg.device}')
############# 由于测试不需要使用epsilon-greedy策略,所以相应的值设置为0 ###############
cfg.epsilon_start = 0.0 # e-greedy策略中初始epsilon
cfg.epsilon_end = 0.0 # e-greedy策略中的终止epsilon
################################################################################
rewards = [] # 记录所有回合的奖励
steps = []
for i_ep in range(cfg.test_eps):
ep_reward = 0 # 记录一回合内的奖励
ep_step = 0
state = env.reset() # 重置环境,返回初始状态
while True:
ep_step+=1
action = agent.sample(state) # 选择动作
next_state, reward, done, _ = env.step(action) # 更新环境,返回transition
state = next_state # 更新下一个状态
ep_reward += reward # 累加奖励
if done:
break
steps.append(ep_step)
rewards.append(ep_reward)
print(f'Episode:{i_ep+1}/{cfg.test_eps}, Reward:{ep_reward:.2f}, Step:{ep_step:.2f}')
print('完成测试!')
env.close()
return {'rewards':rewards,'steps':steps}
cfg = Config()
# 训练
env, agent = env_agent_config(cfg)
res_dic = train(cfg, env, agent)
make_dir(cfg.result_path, cfg.model_path) # 创建保存结果和模型路径的文件夹
agent.save(path=cfg.model_path) # 保存模型
save_results(res_dic, tag='train',
path=cfg.result_path) # 保存结果
plot_rewards(res_dic['rewards'],cfg , path=cfg.result_path , tag="train") # 画出结果
# 测试
env, agent = env_agent_config(cfg)
agent.load(path=cfg.model_path) # 导入模型
res_dic = test(cfg, env, agent)
save_results(res_dic, tag='test',
path=cfg.result_path) # 保存结果
plot_rewards(res_dic['rewards'],cfg , path=cfg.result_path , tag="test") # 画出结果
Noisy,Distribution,Rainbow代码
这一份代码也是多用的。同样,拼接以后调了bug才能用,这里给的是拼接后的版本。
这个代码我研究的不是很透,Noisy需要的基本功比较强,编写的很复杂,我改不动。
import sys
import os
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
import torchvision.transforms as transforms
from torch.autograd import Variable
#curr_path = os.path.dirname(os.path.abspath(__file__)) # 当前文件所在绝对路径
curr_path=os.getcwd()
parent_path = os.path.dirname(curr_path) # 父路径
sys.path.append(parent_path) # 添加路径到系统路径
import gym
import torch
import datetime
import numpy as np
import math
import random
import os
import numpy as np
from pathlib import Path
import matplotlib.pyplot as plt
import seaborn as sns
import json
import pandas as pd
from matplotlib.font_manager import FontProperties # 导入字体模块
'''
from common.utils import save_results_1, make_dir
from common.utils import plot_rewards
'''
curr_time = datetime.datetime.now().strftime("%Y%m%d-%H%M%S") # 获取当前时间
def make_dir(*paths):
''' 创建文件夹
'''
for path in paths:
Path(path).mkdir(parents=True, exist_ok=True)
def save_results(res_dic, tag='train', path = None):
''' 保存奖励
'''
Path(path).mkdir(parents=True, exist_ok=True)
df = pd.DataFrame(res_dic)
df.to_csv(f"{path}/{tag}ing_results.csv",index=None)
print('Results saved!')
def smooth(data, weight=0.9):
'''用于平滑曲线,类似于Tensorboard中的smooth
Args:
data (List):输入数据
weight (Float): 平滑权重,处于0-1之间,数值越高说明越平滑,一般取0.9
Returns:
smoothed (List): 平滑后的数据
'''
last = data[0] # First value in the plot (first timestep)
smoothed = list()
for point in data:
smoothed_val = last * weight + (1 - weight) * point # 计算平滑值
smoothed.append(smoothed_val)
last = smoothed_val
return smoothed
def plot_rewards(rewards,cfg,path=None,tag='train'):
sns.set()
plt.figure() # 创建一个图形实例,方便同时多画几个图
plt.title(f"{tag}ing curve on {cfg.device} of {cfg.algo_name} for {cfg.env_name}")
plt.xlabel('epsiodes')
plt.plot(rewards, label='rewards')
plt.plot(smooth(rewards), label='smoothed')
plt.legend()
if cfg.save_fig:
plt.savefig(f"{path}/{tag}ing_curve.png")
if cfg.show_fig:
plt.show()
class ReplayBuffer:
def __init__(self, capacity):
self.capacity = capacity # 经验回放的容量
self.buffer = [] # 缓冲区
self.position = 0
def push(self, state, action, reward, next_state, done):
''' 缓冲区是一个队列,容量超出时去掉开始存入的转移(transition)
'''
if len(self.buffer) < self.capacity:
self.buffer.append(None)
self.buffer[self.position] = (state, action, reward, next_state, done)
self.position = (self.position + 1) % self.capacity
def sample(self, batch_size):
batch = random.sample(self.buffer, batch_size) # 随机采出小批量转移
state, action, reward, next_state, done = zip(*batch) # 解压成状态,动作等
return state, action, reward, next_state, done
def __len__(self):
''' 返回当前存储的量
'''
return len(self.buffer)
class NoisyLinear(nn.Module):
def __init__(self, input_dim, output_dim, device, std_init=0.4):
super(NoisyLinear, self).__init__()
self.device = device
self.input_dim = input_dim
self.output_dim = output_dim
self.std_init = std_init
self.weight_mu = nn.Parameter(torch.FloatTensor(output_dim, input_dim))
self.weight_sigma = nn.Parameter(torch.FloatTensor(output_dim, input_dim))
self.register_buffer('weight_epsilon', torch.FloatTensor(output_dim, input_dim))
self.bias_mu = nn.Parameter(torch.FloatTensor(output_dim))
self.bias_sigma = nn.Parameter(torch.FloatTensor(output_dim))
self.register_buffer('bias_epsilon', torch.FloatTensor(output_dim))
self.reset_parameters()
self.reset_noise()
def forward(self, x):
if self.device==torch.device('cuda'):
weight_epsilon = self.weight_epsilon.cuda()
bias_epsilon = self.bias_epsilon.cuda()
else:
weight_epsilon = self.weight_epsilon
bias_epsilon = self.bias_epsilon
if self.training:
weight = self.weight_mu + self.weight_sigma.mul(Variable(weight_epsilon))
bias = self.bias_mu + self.bias_sigma.mul(Variable(bias_epsilon))
else:
weight = self.weight_mu
bias = self.bias_mu
return F.linear(x, weight, bias)
def reset_parameters(self):
mu_range = 1 / math.sqrt(self.weight_mu.size(1))
self.weight_mu.data.uniform_(-mu_range, mu_range)
self.weight_sigma.data.fill_(self.std_init / math.sqrt(self.weight_sigma.size(1)))
self.bias_mu.data.uniform_(-mu_range, mu_range)
self.bias_sigma.data.fill_(self.std_init / math.sqrt(self.bias_sigma.size(0)))
def reset_noise(self):
epsilon_in = self._scale_noise(self.input_dim)
epsilon_out = self._scale_noise(self.output_dim)
self.weight_epsilon.copy_(epsilon_out.ger(epsilon_in))
self.bias_epsilon.copy_(self._scale_noise(self.output_dim))
def _scale_noise(self, size):
x = torch.randn(size)
x = x.sign().mul(x.abs().sqrt())
return x
class MLP(nn.Module):
def __init__(self, n_states,n_actions,hidden_dim=128):
""" 初始化q网络,为全连接网络
n_states: 输入的特征数即环境的状态维度
n_actions: 输出的动作维度
"""
super(MLP, self).__init__()
self.fc1 = nn.Linear(n_states, hidden_dim) # 输入层
self.fc2 = nn.Linear(hidden_dim,hidden_dim) # 隐藏层
self.fc3 = nn.Linear(hidden_dim, n_actions) # 输出层
def forward(self, x):
# 各层对应的激活函数
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
return self.fc3(x)
class RainbowModel(nn.Module):
def __init__(self, n_states, n_actions, n_atoms, Vmin, Vmax, cfg):
super(RainbowModel, self).__init__()
self.n_states = n_states
self.n_actions = n_actions
self.n_atoms = n_atoms
self.Vmin = Vmin
self.Vmax = Vmax
self.linear1 = nn.Linear(n_states, 32)
self.linear2 = nn.Linear(32, 64)
self.noisy_value1 = NoisyLinear(64, 64, device=cfg.device)
self.noisy_value2 = NoisyLinear(64, self.n_atoms, device=cfg.device)
self.noisy_advantage1 = NoisyLinear(64, 64, device=cfg.device)
self.noisy_advantage2 = NoisyLinear(64, self.n_atoms * self.n_actions, device=cfg.device)
def forward(self, x):
batch_size = x.size(0)
x = F.relu(self.linear1(x))
x = F.relu(self.linear2(x))
value = F.relu(self.noisy_value1(x))
value = self.noisy_value2(value)
advantage = F.relu(self.noisy_advantage1(x))
advantage = self.noisy_advantage2(advantage)
value = value.view(batch_size, 1, self.n_atoms)
advantage = advantage.view(batch_size, self.n_actions, self.n_atoms)
x = value + advantage - advantage.mean(1, keepdim=True)
x = F.softmax(x.view(-1, self.n_atoms)).view(-1, self.n_actions, self.n_atoms)
return x
def reset_noise(self):
self.noisy_value1.reset_noise()
self.noisy_value2.reset_noise()
self.noisy_advantage1.reset_noise()
self.noisy_advantage2.reset_noise()
def act(self, state):
state = Variable(torch.FloatTensor(state).unsqueeze(0), volatile=True)
dist = self.forward(state).data.cpu()
dist = dist * torch.linspace(self.Vmin, self.Vmax, self.n_atoms)
action = dist.sum(2).max(1)[1].numpy()[0]
return action
class RainbowDQN(nn.Module):
def __init__(self, n_states, n_actions, n_atoms, Vmin, Vmax,cfg):
super(RainbowDQN, self).__init__()
self.n_states = n_states
self.n_actions = n_actions
self.n_atoms = cfg.n_atoms
self.Vmin = cfg.Vmin
self.Vmax = cfg.Vmax
self.policy_model = RainbowModel(n_states, n_actions, n_atoms, Vmin, Vmax, cfg)
self.target_model = RainbowModel(n_states, n_actions, n_atoms, Vmin, Vmax, cfg)
self.batch_size = cfg.batch_size
self.memory = ReplayBuffer(cfg.memory_capacity) # 经验回放
self.optimizer = optim.Adam(self.policy_model.parameters(), 0.001)
def choose_action(self,state):
state = Variable(torch.FloatTensor(state).unsqueeze(0), volatile=True)
dist = self.policy_model(state).data.cpu()
dist = dist * torch.linspace(self.Vmin, self.Vmax, self.n_atoms)
action = dist.sum(2).max(1)[1].numpy()[0]
return action
def projection_distribution(self,next_state, rewards, dones):
delta_z = float(self.Vmax - self.Vmin) / (self.n_atoms - 1)
support = torch.linspace(self.Vmin, self.Vmax, self.n_atoms)
next_dist = self.target_model(next_state).data.cpu() * support
next_action = next_dist.sum(2).max(1)[1]
next_action = next_action.unsqueeze(1).unsqueeze(1).expand(next_dist.size(0), 1, next_dist.size(2))
next_dist = next_dist.gather(1, next_action).squeeze(1)
rewards = rewards.unsqueeze(1).expand_as(next_dist)
dones = dones.unsqueeze(1).expand_as(next_dist)
support = support.unsqueeze(0).expand_as(next_dist)
Tz = rewards + (1 - dones) * 0.99 * support
Tz = Tz.clamp(min=self.Vmin, max=self.Vmax)
b = (Tz - self.Vmin) / delta_z
l = b.floor().long()
u = b.ceil().long()
offset = torch.linspace(0, (self.batch_size - 1) * self.n_atoms, self.batch_size).long()\
.unsqueeze(1).expand(self.batch_size, self.n_atoms)
proj_dist = torch.zeros(next_dist.size())
proj_dist.view(-1).index_add_(0, (l + offset).view(-1), (next_dist * (u.float() - b)).view(-1))
proj_dist.view(-1).index_add_(0, (u + offset).view(-1), (next_dist * (b - l.float())).view(-1))
return proj_dist
def update(self):
if len(self.memory) < self.batch_size: # 当memory中不满足一个批量时,不更新策略
return
state, action, reward, next_state, done = self.memory.sample(self.batch_size)
state = Variable(torch.FloatTensor(np.float32(state)))
next_state = Variable(torch.FloatTensor(np.float32(next_state)), volatile=True)
action = Variable(torch.LongTensor(action))
reward = torch.FloatTensor(reward)
done = torch.FloatTensor(np.float32(done))
proj_dist = self.projection_distribution(next_state, reward, done)
dist = self.policy_model(state)
action = action.unsqueeze(1).unsqueeze(1).expand(self.batch_size, 1, self.n_atoms)
dist = dist.gather(1, action).squeeze(1)
dist.data.clamp_(0.01, 0.99)
loss = -(Variable(proj_dist) * dist.log()).sum(1)
loss = loss.mean()
self.optimizer.zero_grad()
loss.backward()
self.optimizer.step()
self.policy_model.reset_noise()
self.target_model.reset_noise()
def save(self, path): # 保存目标网络
torch.save(self.target_model.state_dict(), path+'checkpoint.pth')
def load(self, path):
self.target_model.load_state_dict(torch.load(path+'checkpoint.pth'))
for target_param, param in zip(self.target_model.parameters(), self.policy_model.parameters()):
param.data.copy_(target_param.data)
class Config:
'''超参数
'''
def __init__(self):
############################### hyperparameters ################################
self.algo_name = 'DQN' # algorithm name
self.env_name = 'CartPole-v0' # environment name
self.device = torch.device(
"cuda" if torch.cuda.is_available() else "cpu") # check GPU
self.seed = 10 # 随机种子,置0则不设置随机种子
self.train_eps = 500 # 训练的回合数
self.test_eps = 20 # 测试的回合数
################################################################################
self.noisy = False
################################## 算法超参数 ###################################
self.gamma = 0.95 # 强化学习中的折扣因子
self.epsilon_start = 0.90 # e-greedy策略中初始epsilon
self.epsilon_end = 0.01 # e-greedy策略中的终止epsilon
self.epsilon_decay = 500 # e-greedy策略中epsilon的衰减率
self.lr = 0.0001 # 学习率
self.memory_capacity = 100000 # 经验回放的容量
self.batch_size = 64 # mini-batch SGD中的批量大小
self.target_update = 4 # 目标网络的更新频率
self.hidden_dim = 256 # 网络隐藏层
self.n_atoms=5
self.Vmin=0
self.Vmax=2
################################################################################
################################# 保存结果相关参数 ################################
self.result_path = curr_path + "/outputs/" + self.env_name + \
'/' + curr_time + '/results/' # 保存结果的路径
self.model_path = curr_path + "/outputs/" + self.env_name + \
'/' + curr_time + '/models/' # 保存模型的路径
self.save_fig = True # 是否保存图片
self.show_fig = True
self.print_res_epi = 20 # 输出结果的频率
################################################################################
def env_agent_config(cfg):
''' 创建环境和智能体
'''
env = gym.make(cfg.env_name) # 创建环境
n_states = env.observation_space.shape[0] # 状态维度
n_actions = env.action_space.n # 动作维度
print(f"n states: {n_states}, n actions: {n_actions}")
agent=RainbowDQN(n_states,n_actions,cfg.n_atoms,cfg.Vmin,cfg.Vmax,cfg)
if cfg.seed !=0: # 设置随机种子
torch.manual_seed(cfg.seed)
env.seed(cfg.seed)
np.random.seed(cfg.seed)
return env, agent
def train(cfg, env, agent):
''' 训练
'''
print('开始训练!')
print(f'环境:{cfg.env_name}, 算法:{cfg.algo_name}, 设备:{cfg.device}')
rewards = [] # 记录所有回合的奖励
steps = []
for i_ep in range(cfg.train_eps):
ep_reward = 0 # 记录一回合内的奖励
ep_step = 0
state = env.reset() # 重置环境,返回初始状态
while True:
ep_step += 1
action=agent.choose_action(state)
#action = agent.sample(state) # 选择动作
next_state, reward, done, _ = env.step(action) # 更新环境,返回transition
agent.memory.push(state, action, reward,
next_state, done) # 保存transition
state = next_state # 更新下一个状态
agent.update() # 更新智能体
ep_reward += reward # 累加奖励
if done:
break
if (i_ep + 1) % cfg.target_update == 0: # 智能体目标网络更新
agent.target_model.load_state_dict(agent.policy_model.state_dict())
steps.append(ep_step)
rewards.append(ep_reward)
if (i_ep + 1) % cfg.print_res_epi == 0:
print(f'Episode:{i_ep+1}/{cfg.train_eps}, Reward:{ep_reward:.2f}, Step:{ep_step:.2f}')
print('Finish training!')
env.close()
res_dic = {'rewards':rewards,'steps':steps}
return res_dic
def test(cfg, env, agent):
print('开始测试!')
print(f'环境:{cfg.env_name}, 算法:{cfg.algo_name}, 设备:{cfg.device}')
############# 由于测试不需要使用epsilon-greedy策略,所以相应的值设置为0 ###############
cfg.epsilon_start = 0.0 # e-greedy策略中初始epsilon
cfg.epsilon_end = 0.0 # e-greedy策略中的终止epsilon
################################################################################
rewards = [] # 记录所有回合的奖励
steps = []
for i_ep in range(cfg.test_eps):
ep_reward = 0 # 记录一回合内的奖励
ep_step = 0
state = env.reset() # 重置环境,返回初始状态
while True:
ep_step+=1
action = agent.choose_action(state) # 选择动作
next_state, reward, done, _ = env.step(action) # 更新环境,返回transition
state = next_state # 更新下一个状态
ep_reward += reward # 累加奖励
if done:
break
steps.append(ep_step)
rewards.append(ep_reward)
print(f'Episode:{i_ep+1}/{cfg.test_eps}, Reward:{ep_reward:.2f}, Step:{ep_step:.2f}')
print('完成测试!')
env.close()
return {'rewards':rewards,'steps':steps}
cfg = Config()
# 训练
env, agent = env_agent_config(cfg)
res_dic = train(cfg, env, agent)
make_dir(cfg.result_path, cfg.model_path) # 创建保存结果和模型路径的文件夹
agent.save(path=cfg.model_path) # 保存模型
save_results(res_dic, tag='train',
path=cfg.result_path) # 保存结果
plot_rewards(res_dic['rewards'],cfg , path=cfg.result_path , tag="train") # 画出结果
# 测试
env, agent = env_agent_config(cfg)
agent.load(path=cfg.model_path) # 导入模型
res_dic = test(cfg, env, agent)
save_results(res_dic, tag='test',
path=cfg.result_path) # 保存结果
plot_rewards(res_dic['rewards'],cfg , path=cfg.result_path , tag="test") # 画出结果
实验报告
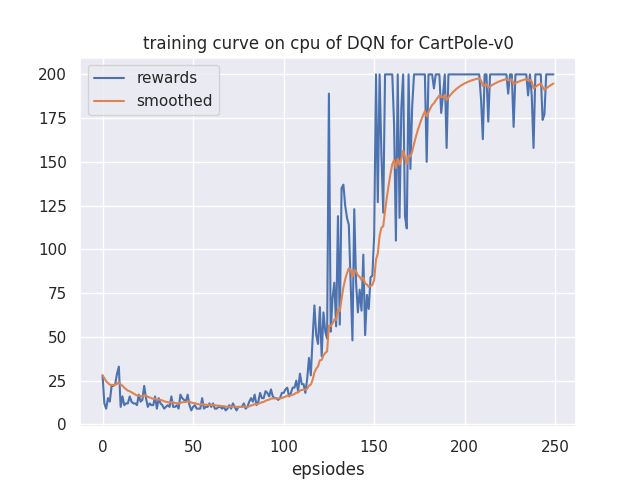
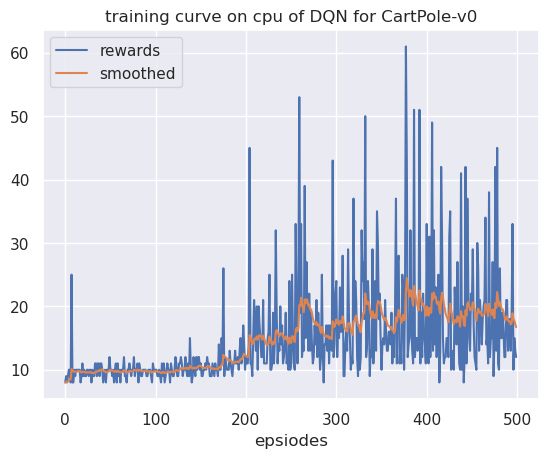
DQN
在CartPole下,我首先使用清晰度比较高的方法编写了基本DQN。之后逐步增加,测试,最后形成RainBow代码。先给出DQN的baseline,接下来针对每一种方法阐述我的理解与实验。
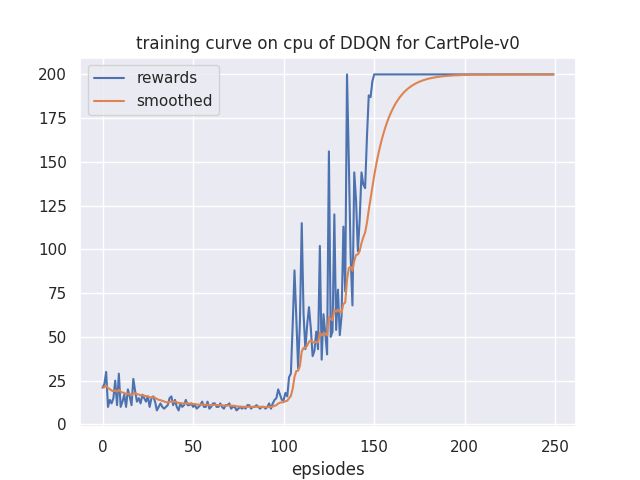
Double DQN(DDQN)
算法理解
Q网络计算出的Q值,在训练过程中整体会随着对各种情况的探索而不断增大。但是就像人学习一样,刚开始啥也不知道,中间是知道一些,就开始膨胀,最后彻底明白了,才能放平心态。机器的训练是无法做到彻底明白的(无法穷举),那么这种策略必然会导致高估Q值(有一些隐藏的情况没有被探索到),估计的Q值高于实际获取的价值。
DDQN算法可以拉进估计值与真实值的距离。
从数学的角度来说,目标Q值的计算是会有误差的。假设目标有4个action,当前状态肯定要选择一个能使目标Q最大的action。问题就出在,假设第一个动作的实际Q值低于第二个动作,但是估计出来的Q值更大,那么当前状态就会选择第一个动作作为目标Q值的参数。
那么结果无非是几种:
- 都没有高估
- 可变网络高估了,目标网络没高估。虽然选错了动作,但是目标网络给这个不好的动作打了低分,目标Q值也不会高估。
- 可变网络没高估,目标网络高估(假设b动作高估,a动作正常)。动作没选错(假设选了a),虽然目标网络b高估了,但是我不去算b,而是算a,仍然是正常的目标Q值。
- 可变网络和目标网络都高估。回归了DQN的错误情形。
由此可见,以前是55开的高估可能,现在高估可能只有26开了,提高了对高估的容错率。实现起来也特别简单,改一下公式就可以,所以如果只能选一个技巧的话,就用DDQN就很方便。
结果
结果显示,DDQN可以明显提高训练速度与表现。
深度竞争Q网络(dueling DQN)
算法理解
基础Q网络,是输入S-A,得到标量Q,或者输入S,得到向量,对应所有action的Q向量。深度竞争Q网络,不直接输出Q值,而是分成两路计算,一路计算一个V值,一路计算A向量。V值可以理解为一个状态的平均收益,类似于状态价值函数。而A值可以理解为在一个状态下,采取不同action对收益带来的波动。这个波动有正有负。
这有什么用呢?首先,本身就是合理的。其次,如果每次迭代,主要是更新V值,那么就不需要采样S状态下所有的action就可以更新所有action的Q值,这样的效率更高,这也是这个方法的关键效果:加速。
其实这里有个隐含的问题。逻辑上合理,并不代表网络会朝着你期望的角度去发展。毕竟,如果最后V值恒等于0,那A不就和Q一样了吗?这种情况完全有可能出现。为了防止这种情况出现,我们要给A加一个限制,即总和为0,直接给他归一化即可,均值归0,方差不变。
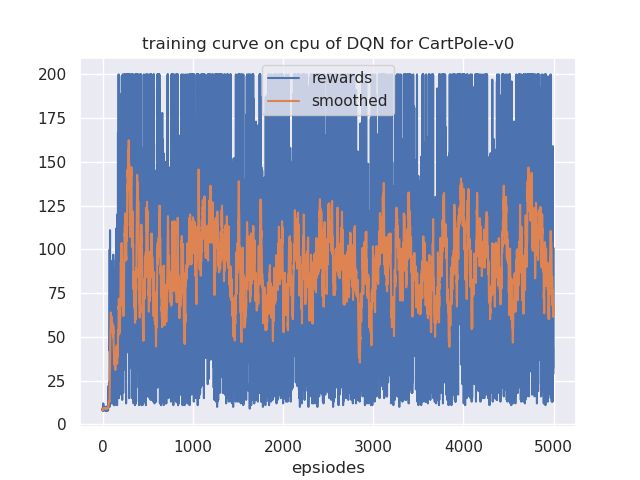
初步结果
DuelingDQN的结果如下,可以看到,收敛的速度明显提升,印证了前面的“加速”猜想。
退化猜想
前面的算法中提出了,如果不加归一化可能会导致退化为DQN的情况。于是我尝试了一下,修改的代码如下。结果显示,不加归一化其实不会导致明显的退化。无论是从V的输出还是从图像来说。
优先级经验回放(PER,prioritized experience replay)
算法理解
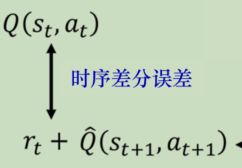
我们训练的方式是回归,如果预测和目标差距不大,那么相当于已经回归得不错了,没必要继续算下去了。
从经验的角度来看,就是这一笔经验已经没用了,无法对训练产生效果了,所以在从经验回放池中选择的时候,这种无用经验就可以放弃了,或者给一个较低的概率。反过来,如果差距大,那么这笔经验就有较大的训练价值,就应该给更大的概率,即优先权。
算法实现
具体怎么实现呢?
首先,肯定是要修改那个sample函数。但是具体怎么做书里没说,我给一种思路:
- 假设最终要选batch_size个经验
- 我先随机选出k×batch_size个经验
- 然后把这些经验的Q值都算出来,并计算出与目标的差距
- 选差距最大的batch_size个,或者归一化后按照概率采样batch_size个
用这种思路写了一下,结果是target_value越来越大,q_value反而增长不显著,甚至出现反向减弱的趋势,原因不明,我觉得可能是BP我的代码写的有一些bug,造成了BP调节目标出错。因为时间原因,就没有继续进行优先级经验回放的实验了。
噪声网络(noisy net)
算法理解
- epsilon是给动作空间加噪声,就好像是,意外的不可抗力逼着你不得不采取某些策略(随机策略),即使你想要做预期的决策,最后也可能因为意外也无法落实。
- 噪声网络是在参数空间加噪声,扰动你对S-A的评估,你虽然是心想事成,但是这个决策可能压根就是误判。
epsilon和噪声网络还有一个区别:
- epsilon在每个step都会扰动一次。epsilon让智能体在任何时刻都是不稳定的。
- 噪声网络只会在episode开始施加,在episode内部是不变的。只有到了新的episode才会重新生成扰动。噪声网络就是,一个人在一段时间(一个回合)内,状态是稳定的,但是不同的时间段内,状态有所波动。
从效果上来说:
- epsilon的扰动比较混乱
- 噪声网络更加系统,对于同一个状态,就好像是这个回合向左试试,另一个回合向右试试。
这两种扰动孰优孰劣,难以比较,因为噪声网络刻画的是智能体的不稳定性,epsilon是环境的不稳定性。如果没有环境的不确定性,那么这种搜索就叫依赖状态的搜索(state-dependent exploration),即心想事成。
算法实现
具体怎么做?
- OpenAI的方法比较简单。直接给所有参数都加一个规定均值方差的高斯噪声
- DeepMind方法更复杂。高斯噪声的参数还可以根据训练得到
但是无论如何,回合内噪声都是不变的。
理论虽然很好,但是结果并不是特别好,图像呈现如下特点:
- 前期的smooth曲线会有一个上升趋势
- 中后期,smooth曲线无法稳定
- 在中后期,实际上未经过滑动平均的train曲线基本保持在200的满分状态,只不过会有剧烈的跳动,这才造成了smooth曲线无法稳定。
使用噪声网络后,网络难以收敛,我的猜测是,epsilon-greedy会随着采样次数增加而收敛,此时算法趋近于贪心,会以比较快的速度收敛。但是我的实现中,噪声不会随着时间推移而收敛,这就导致算法需要训练很长时间,而且最后的效果也不会收敛。
我的建议是,给噪声增加一个收敛的特性加速算法收敛,类似于epsilon-greedy的收敛因子,这样,训练到中后期的噪声网络就可以快速收敛,稳定。
分布式Q函数(distributed Q-function)
算法理解
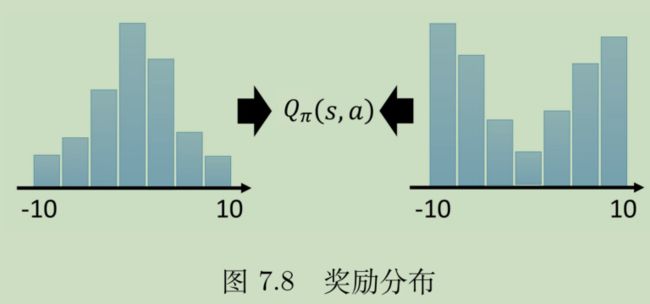
环境是有随机性的,奖励其实也应该具有随机性。可以说,即使是同一个S-A,在现实中的Q都是不一样的。涉及到了概率,原来的Q值可以理解为一个期望,那么实际上Q(S,A)应当是一个分布。
下图给出了两种概率分布,其均值相同,但是实际确实完全不同的分布,Q的意义也完全不同。如果简单的用标量衡量,就无法对环境的随机性建模。
如何给环境建模呢?或者说如何把Q值变成一个分布呢?理想情况应该是一个概率密度分布,但是实际上我们只能给出离散化的近似概率密度分布。
- 对于每一个S-A,可以把Q值的可能区间切分成k份。即,将Q网络的输出从n维向量变成n×k维向量。
- 比如就是-10到10,切成5份,以区域中心的值代表这个区域的均值,高度对应概率
区间调参
修改了网络结构后怎么用呢?
- 可以用在action选择上,根据分布的方差来判断这个action的风险大不大。
- 至于Q值计算,其实还是用均值的,当然,也可以用分布去采样一个S-A对应的Q值。
从具体实现来讲,不是特别好实现,尤其是区间的确定是非常重要的。如果使用-100到100的区间,结果会非常糟糕,这是因为Q值的分布只占-100到100的一个很小的区域,用过大的区域去训练,会干扰对Q值的计算。
如果区间太小,用0-2的区间,效果也会很差,因为0-2不足以表达Q值,Q值的上限要远大于2。
最佳范围
之后我产生了一个新的想法,先用普通方法训练一次,把训练过程中的Q均值画成曲线,然后估计一下,再用分布式训练。经过我的测试,Q值会从0到20变化,于是我取了0-20的区间,在有噪声网络的情况下,可以和DDQN达到同一水平。
RainBow
把前面几种方法综合起来,就是RainBow。总整体趋势来看,RainBow效果是不错的。