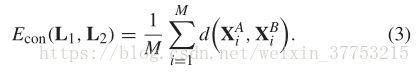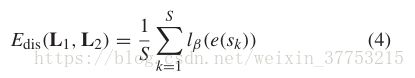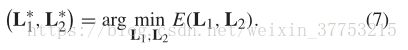Re-id via Discrepancy Matrix and Matrix Metric（IEEE Transactions on Cybernetics 2017）

Abstract

        行人再识别（re-id）作为视频监控和取证应用中的一项重要任务，已得到广泛研究。先前用于解决行人再识别问题的研究工作主要集中于通过利用外观特征来构建稳健的向量描述，或者通过标记的向量来学习判别距离度量。基于人类的认知和识别过程，我们提出了一种新的模式，将特征描述从特征向量转换为差异矩阵。特别是，为了很好地识别行人，它将距离度量从向量度量转换为矩阵度量，矩阵度量由类内差异投影和类间差异投影部分组成。我们引入一致项和判别项来形成目标函数。为了有效地解决它，我们在交替优化过程中针对两个投影使用简单的梯度下降方法。公共数据集的实验结果证明了与最先进的方法相比，所提出的方法的有效性。

关键词： 差异矩阵； 矩阵度量；度量投影；行人再识别

1、Inroduction

            行人再识别（re-id）是视觉上匹配从非重叠场景分布的不同摄像头中同一行人的图像任务[1]。 由于其在视频监控中的重要应用[10] - [12]，近年来引起了人们的极大关注[10] - [12]。虽然人脸[13] - [16]和步态[17]，[18]可能作为识别人的更可靠的生物识别技术，但是由于低分辨率和典型监控场景中个体的姿势变化，它们总是不可用[19] - [21]。 因此，行人再识别主要利用人体的外表。 通常，给定从摄像头A拍摄的探针行人图像，行人再识别算法旨在从摄像机B捕获的候选集中搜索同一行人的图像。用于解决行人再识别问题的先前研究工作主要集中在以下两个方面。   

         A：特征描述

         已经提出了许多方法来开发有辨别力的视觉描述子，这些描述在各种摄像头中可以区分不同的行人，例如局部特征集合（ELF）[22]，基于对称驱动累积的局部特征（SDALF）[23]，基于显著颜色名的颜色描述子（SCNCD）[24]，局部最大发生概率描述子（LOMO）[25]，高斯---高斯（GoG）描述符[26]和深度卷积神经网络（CNN）方法[27] - [31]。 通常，特征向量总是用于通过这些方法描述图像I [32]，其中表示特征维度。

        注：之前的工作所用的特征主要有：ensemble of localized features (ELF)、 symmetry-driven accumulation of local features (SDALF)、 salient color-name-based color descriptor (SCNCD) 、local maximal occurrence (LOMO)、 Gaussian of Gaussian (GoG) descriptor 、 deep convolutional neural network (CNN)approaches。

         b：距离度量

        在学习最佳匹配度量方面还有许多成果，在这些度量下，属于同一个人的实例比属于不同人的实例更接近，例如概率相对距离比较（PRDC）[19]，保持简单直接的度量学习（KISSME） [33]，局部自适应决策函数（LADF）[34]，局部Fisher判别分析（LFDA）[35]和交叉视点二次判别分析（XQDA）[25]。一般而言，多数方法会学习一个度量矩阵M，然后图像对的距离可以被计算出来。上标A，B表示摄像头的标签，p,q表示行人ID。实际上，通过对特征值进行分解，距离可以被写为（1）式。通过这个定义，很容易看出基于度量学习的方法的本质是寻找将原始图像特征转换为新特征空间的投影。

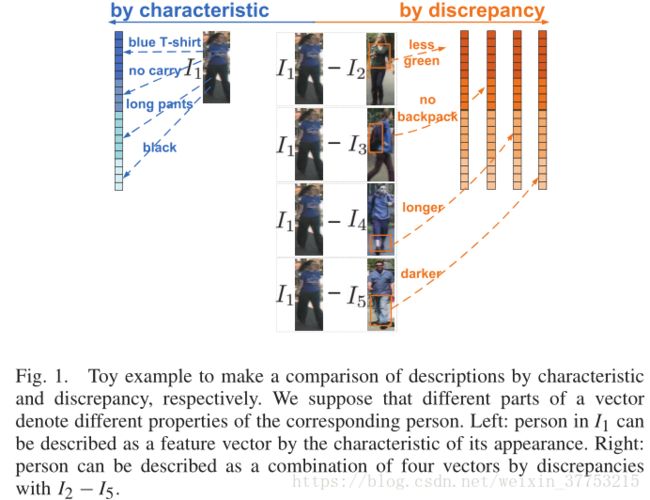
          几乎所有最先进的方法都遵循相同的程序。 它们使用特征向量代表每个行人的图像，无论是手工设计还是深度学习，都基于人的外观。 然后，他们通过特征向量距离比较图像对[36]。 然而，在描述一个人时，我们不仅可以利用他/她自己的外表的特征，而且可以利用与他人的外表关系。最近，An等人[37]提出一种参考描述子reference descriptor（RD）。他们引入了一个参考集，并从参考集中选择典型的身份来重构每个人。重构权重被用来描述相应的行人。在我们看来，RD方法侧重于发现与参考身份整体的全局和粗粒度重建关系，并忽略其与每个参考身份的每个部分的局部差异关系，其具有细粒度并且可能包含重要信息。 我们将差异关系命名为差异。为了描述一个人，本文利用了他/她与参考集的外观差异。 图1示显示了样例。 我们假设向量的不同部分表示相应行人的不同属性。正如图1（左）所示，在传统方法中，I1中的行人被描述为：穿着一件蓝T恤和长裤子，没有背任何东西。上半身是蓝色的且下半身是黑色的。这些特点作为特征被提取。另一方面，我们也可以通过一个人与他人的差异来描述这个行人。让我们看图1（右）。我们用另一种方法来描述图像I1如下：I 2的T恤的颜色与I 1的颜色相比较绿，I 1没有背包，但 I 3持有，I 1的裤子比I 4的裤子长，并且颜色为 I 1的裤子比I 5的裤子暗。因此样例展示了行人不仅可以被他/她的她点所描述，而且可以通过与他人的差异来描述。一般地，我们利用特征向量来表示一个行人。为了这个目标，每两张图像的差异被表示为特征向量的差异，也就是一个减去另外一个。在该样例中，图像I 1由四个差异向量（或差异矩阵）的组合来描述。

       图1.分别通过特征和差异对描述进行比较的样例。 我们假设向量的不同部分表示相应人的不同属性。 左：I 1中的人可以通过其外观的特征被描述为特征向量。 右：行人可以被描述为与I 2 - I 5的差异的四个向量的组合。

       如果两人之间的每种差异由向量表示，则与参考集的所有差异将形成用于描述相应行人的一个矩阵。与参考描述向量[37]相比，差异矩阵捕获更多样化的特征，并且还通过从两个摄像头引入几个参考集来减少由摄像头条件变化引起的影响。详情见第III-B节。在差异矩阵方法中，每个图像对的距离应基于一对差异矩阵进行计算。因此，现有的度量学习方法，其侧重于生成向量度量，显然不适合于所提出的描述。很容易认识到来自同一个人的两个差异矩阵应该彼此相似，而来自不同人的两个差异矩阵应该是不同的。为此，提出了一种有效的矩阵距离度量学习方法，包括类间差异和类内差异投影。

       本文的贡献如下：

         1）从特征向量到差异矩阵。我们提出了一种描述行人图像的新思路，用与一组图像的差异来表示行人图像，而不是图像本身的特征。结果表明，与特征向量相比，差异矩阵具有更好的识别性和有效性；

          2）从向量度量到矩阵度量。提出了一种由类间差异投影部分和类内差异投影部分组成的行人重识别任务矩阵度量方法。在训练阶段，同时考虑一致性约束(将两个差异矩阵从同一个人身上拉出)和判别性约束(将两个差异矩阵从远处推到不同人身上)来学习矩阵度量；

         3）一种新的模式：我们提供了一种新的行人再识别模式，它通过差异矩阵和矩阵度量（Discrepancy Matrix and Matrix Metric）重新识别和排列图像。 对基准数据集的广泛实验评估证明了所提出模式的有效性。 值得注意的是，所提出的行人再识别模式独立于特征描述符的选择。 结合最先进的特征提取方法，例如深度学习方法，可以获得更好的结果。

        本文的其余部分安排如下。 在第二部分，简要回顾了行人再识别的相关工作。 在第三节中，我们介绍了我们方法的动机，并正式定义了新的问题。 在第四节中，我们说明了所提出的矩阵度量学习的细节。 第五节报告实验结果和分析。 最后，第六节总结了本文。 表I总结了本文中使用的符号。

                                                                                           表I 符号说明

2、  RELATED WORK

        在本节中，我们将简要回顾有关行人再识别的相关工作。 当前的行人再识别研究通常可以分为两类：1）基于特征描述和2）基于距离度量的方法。

       特征描述方法旨在构建判别性视觉描述。通常，这种方法可以分为基于手工设计和基于深度学习。行人再识别任务中的手工描述是通过利用行人的特殊外观特征来设计的。Wang等人 [38]研究了一个外观模型来捕捉外观的空间分布。 Gray和Tao [22]使用ELF进行了视点不变描述。 Farenzena等人 [23]通过使用对称性和不对称感知原理描述了具有分割区域的外观图像。 Ma等人 [39]结合了生物启发特征和协方差描述符(BiCov)。 Layne等人 [40]学会了对中级语义属性的选择和加权来描述人。 Kviatkovsky等人[41]使用形状上下文描述符来表示内部分布结构，它们在不同的光照条件下是不变的。Zhao等人[42]以无人监督的方式为每个补丁分配显著性。Yang等人[24]提出了一个SCNCD来代表人的形象。 Eiselein等 [43]融合了多个基本特征，如颜色直方图，SURF [44]，并设计了一个快速有效的行人描述符，满足低运行时的实际需要。 Liao等人 [25]分析局部特征的水平发生，并最大化发生以对视点变化进行稳定表示。 Matsukawa等人 [26]将每个人图像区域建模为一组多个高斯分布，其中每个高斯分布表示局部补丁的外观。 最近，针对行人再识别任务出现了深入学习的描述。Li等人 [27]利用统一的深层架构来学习行人再识别的过滤器。Ding 等人[28]提出了一种基于深度神经网络的可扩展距离驱动特征学习框架。Zhang 等人[29]开发了深度可缩放的散列码来表示原始图像。Wang 等人 [30]结合了四个CNN，每个CNN嵌入来自不同规模或不同身体部位的图像。 总的来说，所有这些方法都集中在人的外观上，并将每个人的图像表示为特征向量。

        除了人物形象本身的特征之外，还可以利用与其他身份的关系。 An等 [37]利用参考集来描述一个人。 然而，他们选择一些典型的参考特征来构造向量，而我们利用差异而不是原始参考特征来形成行人再识别问题的矩阵。

       距离度量方法关注于找到适当的距离度量。 Hirzer等[45]和Dikmen等人[46]采用LMNN [47]来学习行人再识别的最佳度量。Zheng 等人[19]通过PRDC学习了Mahalanobis 距离度量。 Köstinger等[33]使用高斯分布来拟合成对样本并获得更简单的度量函数。Tao 等人[48]通过无缝集成平滑和正则化技术，提出了一种正则化平滑KISS度量学习，用于稳健地估计协方差矩阵。 Mignon和Jurie [49]引入了成对约束分量分析（PCCA）来学习高维输入空间中稀疏成对相似性/不相似性约束的距离度量。 Pedagadi等[35]组合无监督主成分分析（PCA）维数减少和由训练集定义的LFDA来执行度量学习。Li 等人[34]提出学习决策函数，可以将其视为距离度量和局部自适应阈值规则的联合模型。Wang 等人[50]将度量学习问题转换为特征投影矩阵学习问题，该问题将一个摄像头的图像特征投影到另一个摄像头的特征空间。Liao 等人[25]通过XQDA学习了判别式低维子空间。Wang 等人[1]调查了两个摄像头之间的一致性，并调整了每个查询 - 图库对的度量。Zhang 等人[51]提出通过将类内分散最小化到最大化并同时最大化相对类间分离来学习行人再识别的判别零空间。 Zheng和Shao [52]在汉明空间学习了快速行人再识别的距离度量。

      所有这些方法都试图获得特征向量的适当距离度量。 相反，我们提出的方法利用差异矩阵。 因此，我们的问题不能使用专注于生成向量度量而非矩阵度量的传统方法。 为此，提出了一种矩阵度量学习方法。

3、PROBLEM  STATEMENT AND MOTIVATION

      在本节中，我们首先回顾一下行人再识别任务的传统模式。 然后，我们在提出的方法中提出了差异矩阵度量(DM^3)的动机。

A. Feature and Vector Metric 

      对于传统的行人再识别问题，有标记的行人的集合     与两个摄像头关联，其中M是行人的数量。我们表示由摄像头A（或摄像头B）拍摄的行人的代表性描述为或者（），然后，且分别代表摄像头A和B拍摄的有标签的训练集图像。基于这两个集合，一个规则化的距离度量被学习。

           令代表来自摄像头A的一个测试探针数据，并且表示来自摄像头B的测试数据，其中N代表摄像头B中测试数据的数目。然后，对于每个测试探针数据，测试探针数据和每个测试数据之间的距离可以利用（1）进行计算（如图2左列所示）。获取所有距离之后，产生排序列表。

图2. 传统方法和提出的方法之间的比较。对于特征描述和距离度量部分，提出的方法与传统的方法不同。特征描述从向量转换为矩阵。是特征向量的维数，是参考图像的数量。距离度量由特征投影到类内投影和类间投影。

B. Discrepancy Matrix  差异矩阵

      上面提到的一般的方法利用一个人的特征来描述本身的外观。大所述特征描述子将每个行人图像的特征转换为一个判别性的特征向量。我们同样也通过与他人的差异来表示一个行人。给定参考图像特征集合图像I的描述就是构造与图像集合的一系列的特征向量差我们表示描述为：其中是参考集图像的数量。应该注意到[37]和[35]也利用一个参考集合来描述一个行人，并且他们的关注点是从参考集中挑选一些典型的图像并且利用重建参数来产生一个向量描述子。然而，我们的关注点是参考集中所有图像的差异来产生一个矩阵描述子。

     另一方面，两个摄像头的缩放比例，光照改变和拍摄环境的差异造成初始特征描述没有足够的鲁棒性。然而，外界环境对于不同行人的影响也许在相同的摄像头中是相同的。因此，两个特征描述之间的差异也许会减少这些影响。基于这个考虑，我们通过来自相同摄像头的参考集图像集合的特征差异构建差异矩阵描述。特别的，在我们的方法中，两个参考图像集合被选择，这将产生来自A摄像头的图像特征描述和来自B摄像头的图像特征描述，根据定义，如果两个特征描述的下标是相同的，那么该特征是提取自两个不同的摄像头下同一行人的特征。因此，如图2右列所示，对于来自摄像头A的图像，它的差异矩阵描述为。但是对于来自摄像头B的图像来说，它的差异矩阵描述子为这样，特征描述由特征向量转化为差异矩阵。获取到差异矩阵描述之后，我们计算每个描述对的距离。根据[54],我们使用 F范数来衡量差异矩阵的距离。例如，对于图像对，距离是

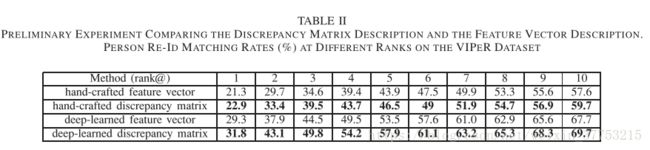
         为了检验差异矩阵描述的有效性，我们进行了初步实验，将其与特征向量描述进行了比较。实验进行了100次。对于每次实验，VIPeR数据集[55]中的100对图像（分别来自于摄像头A和摄像头B）被随机挑选，然后被设定为两个参考图像集。另外的100对图像从剩余的数据集中被随机挑选。每张图像分别被表示为一个特征向量，使用手工设计的GOG描述子[26]和深度学习的微调CNN（FTCNN）描述子[56]，并且之后每张图像的差异矩阵根据之间段落描述的方法被构造。对于特征描述，我们计算每对特征向量的欧式距离。对于矩阵描述，我们计算 每对差异矩阵的矩阵的差的F范数。我们使用CMC曲线[38],该曲线描述发现前r个排序中的真实匹配的期望。结果展示在表II中。从该表，我们可以简单地总结差异矩阵描述比特征向量描述更加有效。我们将改进归因于摄像头条件变化引起的效果降低。原因如下。 在理论上，可以合理地假设虽然有时存在大视点扭曲和遮挡，但是从摄像头A到B，每个人的视觉外观将在一段时间内遇到一致的交叉摄像头成像变化。Kviatkovsky等人[41]提供在不同的光照条件下，每种颜色在对数色度空间中会得到一个约束的变换。Wang等人[1]证明在两个不同的摄像头之间每个行人的变换是一致的。基于这两种方法，我们假定由交叉摄像头成像条件造成的特征差异是相同的，并且定义对每个行人这个一致性的特征差异为v.然后，对于每个参考图像集对，他们的特征差异可以被表示为：其中，表示偏差。同时，对于一对测试图像，他们的特征差异可以被表示为正如我们所知，传统的特征距离由差异决定。它意味着交叉摄像头变量作为一个重要的因素，特别是在成像变量很大时。引入v将很难区分不同的图像对。然而，差异矩阵的距离依赖于其中，交叉摄像头成像变量被移除。不考虑变量v，来自于同一行人的偏差总是小鱼来自不同行人的偏差，这使得行人再识别变得相当简单。因此，它有助于提高差异矩阵描述的表现。

                                                                                                表II

                      比较差异矩阵描述和向量描述效果的初步实验。 在VIPER数据集上的不同排名的行人匹配率（％）

          此外，实验还表明，对于这两种类型的描述（即，向量描述和矩阵描述），结果排在前十位的样本是不同的，并且差异比率是12.84％。 这表明差异矩阵描述和特征向量描述的判别能力是不同的，可能是由于差异矩阵描述引入除行人自身的特征表示之外的图像关系。

C. Matrix Metric

         在不考虑元素的差异或元素的关系的情况下，标准的非训练度量可能不合适。 训练的度量是必要的，以使来自同一个行人的两个矩阵描述的距离较小，而来自不同人的两个矩阵描述的距离较大。对于传统的向量度量学习，如（1）证明，L是一个投影矩阵。如果特征向量会被映射到按照这个规则，如果我们引入一个投影在左乘或者

后，差异矩阵会被映射到

         正如我们所知，左乘后的有效性（它会增加每个差异的条目的权重），不同于有乘。实际上，正确的乘法适用于不同差异的条目。考虑到这个不同，我们引入类内差异投影矩阵作为左乘法器以及类间差异投影矩阵作为右乘法器。这两个投影联合形成矩阵度量。

         为了使这两个投影的功能清晰，我们绘制图3来说明左乘法和右乘法如何工作。 差异矩阵的每列代表从相应参考图像生成的差异。 基于矩阵乘法的原理，L1行和差异矩阵得列以元素方式组合。 这意味着L 1适用于每个差异。 然而，L 2适用于不同的差异。 图3还显示出了L2的列和差异矩阵的行（不同差异的相同维度）以元素方式组合。 在本文中，我们介绍了差异间投影，并没有将差异矩阵转换为向量。 原因如下。

       图3.两个投影的图示。 基于矩阵乘法原理，将L 1行与差异矩阵（类内差异）列组合，并将L 2列与差异矩阵行（类间差异）组合。 

      1) Easy to Understand With Independent Physical Meanings:

           如果我们不引入L 2作为右乘数，则每个差异将由L 1相同对待。 但是，我们认为不是全部，而是一些参考图像对距离测量有效。 因此，我们通过利用类间差异投影L 2来稀疏地选择一些典型的差异来改善性能。 在第V-C节中，我们分析了类间差异投影的稀疏性。从实验中我们可以看出，如果人物图像对存在大的变化，例如不同的照明和背景变化，则由投影矩阵L 2选择的可能性很小。 L 2证明了它在选择不同差异方面的能力。 而L 1侧重于加权每个差异的不同维度。 我们认为这两个预测具有独立的物理意义。

      2) Less Parameters and Constraints for L 1 :

           如果通过连接列将矩阵转换为向量，则可以直接利用传统的基于向量的度量学习方法，此外，在这种情况下不需要类间差异投影L 2。 我们认为转换后的差异向量设计度量标准可能有效。 然而，在将矩阵重新形成向量之后，向量的维度将显著增加。 如果我们试图对不同的差异给出不同的贡献，那么应该对L1引入更多的约束。 然后，它将使类内差异投影L 1难以学习。

       3) Convenient to Add Constraints:

        转换后的差异向量的形式将破坏数据矩阵的结构信息，并且将破坏每个差异的独立性。 相反，如果我们保留矩阵的结构，将同时利用L1和L2。 要学习矩阵度量，我们可以选择性地优化两个投影。同时，我们可以独立地为两个预测添加约束。 例如，我们引入一个稀疏项来使投影L 2稀疏。

       对于图像对，使用（2）计算新的距离。这样，距离度量由向量度量转换为矩阵度量

      如图2的右列所示，与传统方法不同，所提出的方法在特征描述中利用矩阵而不是向量，并且在距离度量部分由一对投影（左乘和右乘）组成，而不是单个投影。

IV. PROPOSED MATRIX METRIC LEARNING

       本节介绍我们的矩阵度量学习方法。 我们从针对行人再识别问题的矩阵度量学习开始。 然后，提出了一个由一致性和判别性的术语组成的新目标函数。 考虑到并非所有参考行人都对差异有用，也会在目标函数中引入稀疏项。 同时，我们利用交替优化和梯度下降法来学习度量，并设计了一种基于随机抽样的求解方法来加速优化过程。

A. Definition  

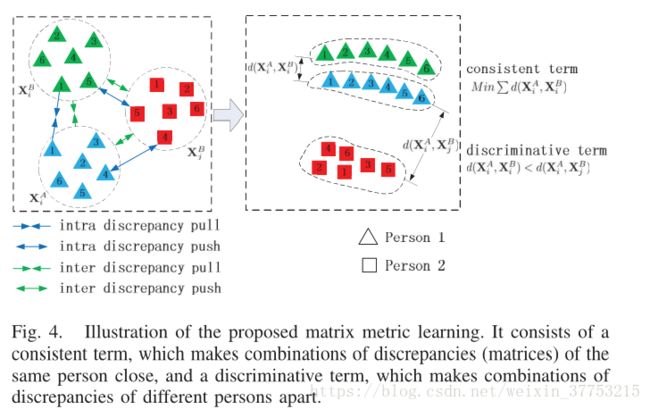
        两个图像之间的新距离定义为（2）。 与（1）相比，在应用投影变换L的情况下，所提出的度量由类内差异投影部分和类间差异投影部分组成。 通常，对于类内差异投影和类间差异投影部分，来自同一个人的每对差异集被拉近，而来自不同人的那些差异集被推开[如图4（左）所示]。给定两个描述子集合和作为训练集，度量学习的本质是在通常包含两个成对约束的监督信息下找到最优L1和L2，即相似约束和不相似约束。

         图4.提出的矩阵度量学习的图示。 它由一个一致的术语组成，它使同一个行人的差异（矩阵）的组合接近，以及一个判别性术语，它将不同行人的差异组合在一起。

B. Objective Function for Matrix Metric Learning

        基于Wang等人[50]的方法，我们用两个术语表达目标函数，并学习矩阵度量L1和L2.第一个术语项目，它来自于同一行人，相互接近，因此有效消除了两台摄像头的不一致性。我们称之为一致的形式。第二个术语项目是远离,其中

它具有度量的判别能力，我们将其称为判别性术语[ 图4（右）]。

          具体地，一致项可以由所有相似对的矩阵距离之和来定义

         直观地，该目标函数中的这个术语惩罚了同一个人的图像之间的大差异矩阵距离。

         在引入判别性术语之前，我们表示三重集合为其中s是集合的大小。然后，对于每个三重样本下面的不等式需要满足.我们对一个三重样本定义一个错误函数为基于这个错误函数，判别性术语被定义为如下形式：

          其中，是广义逻辑损失函数（参考[50]）。很容易看出，目标函数中的这个术语惩罚了侵入不等式的三重样本。 在这里，我们选择逻辑损失函数而不是铰链损失函数有两个原因。 首先，铰链损失在零处是不可微分的，而逻辑损失函数在各处都有导数，这使得解决方案更简单。 其次，逻辑损失给出了铰链损失的软近似，并且更灵活。

         此外，正如第III-C节所讨论的，L2是类间差异投影，作为右乘数控制不同差异的权重。 它选择对差异有用的典型参考行人。 我们认为并非所有的参考行人都对差异有用，而且其中一些人具有更强的辨别力并带来更少的噪音。 因此，差异应该是稀疏的选择[57]。 我们利用范数来改善差异选择[58]，[59]。 通过解决范数最小化问题，L2在每列中都是稀疏的。 稀疏项的表述定义为

           最后，我们结合形式我们三项组合成单个目标函数，用于学习矩阵度量如（6），其中，在本文中，为了简单起见，将一致项和判别项的权重设置为相等，且是稀疏术语的权重

C. Optimization Algorithm

          通过上述目标函数，可以通过求解以下优化问题来学习最优度量：

         由于所提出模型的耦合变量和联合非凸性，无法保证全局最优性。 为了有效地求解模型，我们提出了交替优化过程来迭代地学习L 1和L 2。 与[60]类似，我们固定其中一个投影并优化另一个，然后轮流优化。 我们知道，稀疏项（5）是凸的，如[58]所示。 另外，一致项（3）和判别项（4）基于距离函数（2）。 当我们修正L1或L 2时，原始距离函数从四阶多项式降级为二阶多项式。 因此，（7）可以在关于L1和L2的交替优化处理下使用简单的梯度下降方法来解决。 我们利用随机选择样本的简单随机策略来加快迭代速度，同时保持优化精度。特别的，对于每个正样本，我们随机挑选k（k<目标函数的梯度为

 

    这里，是逻辑损失函数的导数,在上述的公式中，根据[58]，D是对角矩阵，第m个对角线元素为其中，表示L2的第m行。

           利用梯度，可以使用迭代优化算法来学习度量。 从最初的单位矩阵开始，迭代地优化L 1和L 2。 在优化过程中，我们固定一个并更新另一个，如下所示：

        其中，是在每个梯度更新步骤中自动确定的步长。 算法的迭代在达到最大迭代次数（本文中为1000）或符合以下标准时终止：

        其中，是一个小的正值，比如本文取。完整的算法流程图在算法1中展示。

V. EXPERIMENTS

A. Datasets

     1）VIPeR数据集：广泛使用的VIPeR数据集[55]包含从632人的两个视图中获得的1264个室外图像。 一些示例图像显示在图5（a）中。 每个人分别具有从两个不同相机拍摄的一对图像。 将所有个体图像标准化为128×48像素的大小。 视角改变是更改外观的最重要原因。 还包括其他变化，例如照明条件和图像质量。

    2）PRID 450S数据集：PRID 450S数据集[62]是与奥地利技术学院合作创建的，目的是测试行人再识别方法。 这是一个更现实的数据集，其中包含通过两个空间不相交的摄像头视图捕获的450个单个图像对。 所有图像均标准化为168×80像素。 它也是一个具有挑战性的人重新数据集。 与VIPeR数据集不同，此数据集具有显着且一致的光照变化。 PRID 450S数据集中的一些示例如图5（b）所示。

     3）CUHK01数据集：CUHK01数据集[63]是一个较大的数据集，包含来自两个不相交的摄像机视图的971个身份。 每个标识每个摄像机视图有两个样本。 一些示例图像显示在图5（c）中。 共有3884张图片。 所有图像均标准化为160×60像素。 与VIPeR数据集类似，视点改变是外观更改的最重要原因，大多数匹配的图像对包含一个前/后视图和一个侧视图。 由于本文考虑了每个人的每个摄像头视图的单个代表性图像，因此我们在该数据集的实验中为每个人的每个摄像机视图随机选择一个图像。

      图5.三个公共数据集的一些典型样本。 每列显示来自两个不同相机的同一个人的两张图像。 （a）VIPeR数据集。（b）PRID 450S数据集。 （c）CUHK01数据集。

B. Effectiveness of Discrepancy Matrix and Matrix Metric

1) Experimental Settings:

        为了评估所提出的方法，我们使用了GoG描述符[26]并证明了所提出的方法在改造手工制作特征方面的有效性。 同时，鉴于计算机视觉应用中深度学习功能的成功，我们还进行了实验，以证明所提方法对深度学习特征的有效性。 FTCNN [56]描述符用于提取原始特征描述。 这两个特征描述符的常规参数配置相同。 为了加速学习过程并降低噪声，我们进行了PCA以获得低维表示[33]，比如在本次实验中取70（）。然后，差异矩阵使用低维的特征向量产生。我们设定整个评估过程重复十次。CMC[38]曲线常用于计算性能的均值。为了公正地评价和显示提出方法的有效性，我们为每个数据集构建了三个子集，包含训练集，测试机和参考集。这三个子集是非重叠的，并且从整个数据集中随机挑选的。

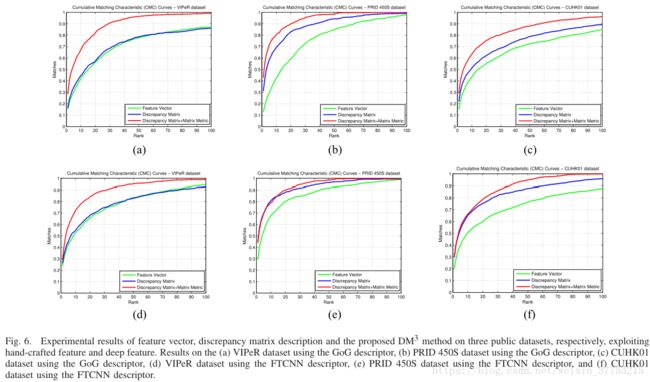
           1) VIPeR Dataset: 对于VIPeR数据集，对于VIPeR数据集，我们随机选择100个样本对作为参考集（N r = 100）。 在一般设置之后，其中训练和测试对的数量相同，分别来自其余样本的200个样本对（M = 200和N = 200）。 得到的结果如图6（a）和（d）所示。 可以看出，差异矩阵的性能优于特征向量，并且所提出的DM ^ 3方法明显优于整个范围内的基本差异矩阵和特征向量。

         2) PRID 450S Dataset: 在VIPeR数据集的评估过程之后，我们分别设置N r = 60，M = 150和N = 150.获得的结果显示在图6（b）和（e）中。 很明显，差异矩阵比特征向量和提出的要好DM ^ 3方法明显优于基本差异矩阵和特征向量。

        3) CUHK01 Dataset: 在对VIPeR数据集的评估过程之后，我们分别设置N r = 100，M = 300和N = 300.图6（c）和（f）给出了不同方法的比较结果。 在这个具有挑战性的CUHK01数据集上，可以根据结果得出与其他两个数据集相同的结论

        这些实验证明，在具有不同特征向量的不同数据集上，所提出的方法表现得非常好。

        图6.特征向量，差异矩阵描述和提出的DM ^ 3方法在三个公共数据集上的实验结果，分别利用手工制作的特征和深度特征。 （a）使用GoG描述符的VIPeR数据集，（b）使用GoG描述符的PRID 450S数据集，（c）使用GoG描述符的CUHK01数据集，（d）使用FTCNN描述符的VIPeR数据集，（e）使用FTCNN描述符PRID 450S数据集的结果，以及（f）使用FTCNN描述符的CUHK01数据集。

C. Sparsity of the Interdiscrepancy Projection   

         如上所述，L2的作用是稀疏地选择对于差异更有用的典型参考。在先前的实验集合中，我们在VIPeR数据集上学习了Nr = 100且M = 200的L2。 图7（a）显示了L2的结果。 从该图中，我们可以看出L 2对于每列是相对稀疏的，也就是说在右乘法之后仅选择了少数参考人。

       在图7（b）中，我们通过分析投影权重列出了一些参考例子。 它们分别是选定的人和未选的人。 比较这些例子，我们认为如果人物图像对存在大的变化，例如不同的照明和背景变化，则由投影矩阵L2选择的可能性很小。

     通过L 2的可视化，该实验表明，一些参考人员对于其他人的差异更有用，具有更多的辨别能力，并且带来更少的噪声。    

       图7.类间投影的稀疏性分析。 （a）可视化类间差异投影。 （b）典型的参考例子。 根据投影矩阵L 2的相应行的值来选择这些示例。 左三列是示例，由具有高值（高权重）的L 2行稀疏地选择。 右三列是具有较小可能性的示例。

D. Evaluating Parameters of the Proposed Method

       我们在不同参数下验证了所提出的方法，包括评估类内差异投影矩阵的贡献的不同参数N 1，以及用于类间差异投影矩阵的不同参数N 2。 该实验在VIPeR数据集上进行，一般配置与前一实验相同。

        我们将N2 = 100固定，并用不同的N1值进行实验。然后，我们将N1 = 70固定，并用不同的N2值进行实验。结果如图8（a）和（b）所示。显然，当N1> 6（N2> 4）时，虽然性能不稳定，但是使用所提出的具有不同N1（N2）值的矩阵度量学习过程仍然可以改善结果。为了一起学习投影L1和L2，我们利用交替优化和梯度下降法，其中不能保证全局最优性。因此，它会使度量标准不完全准确，并且值可能会略有不同。与初始结果相比，在N1 = 1或N2 = 1的情况下，我们认为所提出的矩阵度量以较大的余量证明了其有效性，并且可以接受小的变化。图8（a）和（b）还表明N 1（N 2）不应太小，因为当维数低时，类内差异投影矩阵（类间差异投影矩阵）的度量约束将减小。

     图8.所提方法的参数分析。 VIPeR数据集上的不同（a）N1s的结果，其中N 2 = 100并且（b）在VIPeR数据集上的N2 s，其中N1 = 70。

E. Comparison of the Discrepancy Matrix and the Discrepancy Vector

        通过利用参考集，可以通过多个差分来构建图像的差异描述。 我们在本文中将描述形成为矩阵。 实际上，它也可以重新形成一个长向量。 我们在VIPeR数据集上评估了这两种差异描述。 随机选择50个样品对作为参考组（Nr = 50）。 我们使用GoG描述符[26]作为原始特征描述符，并进行PCA以获得50-D表示（Nf = 50）。作为结果，差异矩阵的描述被定义为但是差异向量的描述为对于前者，两种投影以之前的配置使用。对于后者，由于投影L2会降低并失去其效果，我们仅使用投影L1。 比较结果如图9所示。可以看出，差异矩阵的性能优于将差异矩阵重塑为差异向量。 这可能是因为每个差异的独立性被打破，并且在将矩阵重新形成向量之后，所有差异被平等对待。 当我们将矩阵重塑为向量时，只利用L1。 为了实现L2的有效性，我们应该对不同差异的贡献进行加权，然后应该对L1引入更多约束，本文不考虑这些约束。 相反，如果我们保留矩阵的结构，将同时利用L1和L2。 如第V-C节所述，应通过利用L2稀疏地选择一些典型的差异。

                                                                     图9.差异矩阵和差异向量的比较。

F. Effectiveness of Different Terms

       为了理解不同术语的有效性，我们按照第V-B节中的设置评估了所提出的方法，没有判别项或一致项。所得结果如图10所示。如果提出的方法不使用判别项（ 如图10中的蓝色曲线）或一致的术语（图10中的红色曲线），结果变得更糟，甚至比具有F形距离的基本差异矩阵更差。

      一致的术语将同一个人的样本拉近，并且判别性术语将不同人的样本推向远处。 我们认为如果目标函数没有一致的项，则同一个人的样本分布将被分散，并且类内样本将容易被邻居类间样本混淆。 如果没有判别项的目标函数，则将具有相似外观的不同人的样本拉到一起。 如实验所示，这两个术语都不能省略。

                                                                   图10.没有判别性术语或一致性术语的方法的有效性。

G. Comparing to the State-of-the-Art Re-Id Methods

         在本节中，我们将我们的方法与不同数据集上最先进的行人再识别方法进行了比较。 众所周知，对于大多数数据集，一般设置是选择一半数据集作为训练集，另一半作为测试集。 为了进行公平的比较，我们随机选择了训练集中的一些样本作为参考集。 表III-V分别总结了与VIPeR，PRID450S和CUHK01数据集上的现有技术行人再识别方法的比较结果。     

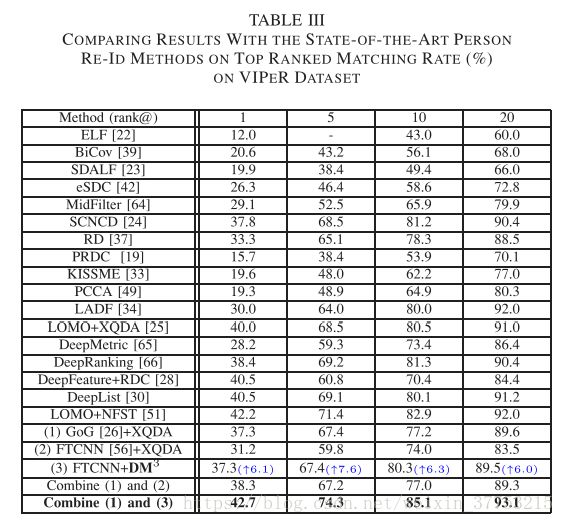
       1) VIPeR Dataset: 按照传统方法，将数据集随机分成两组。一个用于训练（M = 316），另一个用于测试（N = 316）。在训练集中，随机选择参考集Nr = 100。 VIPeR数据集是行人再识别任务最受欢迎的基准数据集，因此，此数据集上的许多最新进度报告结果。我们将我们的方法与以下方法进行比较：ELF [22]，BiCov [39]，SDALF [23]，eSDC [42]，中层滤波器（MidFilter）[64]，SCNCD [24]，RD [37]，PRDC [ 19]，KISSME [33]，PCCA [49]，LADF [34]，LOMO描述符和XQDA（LOMO + XQDA）[25]，深度度量学习（DeepMetric）[65]，DeepRanking [66]，具有相对距离比较的深层特征（DeepFeature + RDC）[28]，具有自适应列表约束的深层特征（DeepList）[30]，具有零空间度量的LOMO描述符（LOMO + NFST）[51]，分层高斯描述符（GoG）[26] XQDA和FTCNN [56]与XQDA。请注意，RD方法使用参考集提取特征描述，但不会利用与参考集的差异。 PRDC方法尝试学习具有样本差异的度量，尽管差异主要集中在描述构造之外的特征距离上。 DeepFeature，DeepMetric，DeepList，DeepRanking和FTCNN是与深度学习框架相关的方法，它们最近获得了良好的性能。使用FTCNN描述符评估所提出的方法（DM^3）。

     所有结果列于表III中。 应该提到：1）GoG + XQDA和 2）FTCNN + XQDA代表传统的行人再识别方法，它使用特征向量（GoG或FTCNN）和向量度量XQDA。 然而，3）FTCNN + DM^3代表利用差异矩阵（基于FTCNN）和矩阵度量DM^3的所提出的方法。 方法1）和2）按照传统方法的程序进行评估，例如[25]。 括号中的蓝色数字表示在给定FTCNN作为特征描述符的情况下，在每个等级处提出的DM^3相对于XQDA的改进。 由于特征和差异矩阵描述，向量和矩阵度量之间的差异，我们通过直接合并两个排名结果融合了所提出的方法（FTCNN + DM^3）和最先进的方法（GoG + XQDA）。 详细地说，融合过程如下。 给定探针图像通过方法1）和3）将会产生两种排序列表。然后，对于摄像头B中的每张图像，我们基于两种排序列表获得它的排序数和，然后以形式结合数量。在获得摄像头B中所有图像的联合数量之后，我们将它们从小到大重新排序，并获得融合排名列表。 如表III所示，融合结果优于其他方法产生的所有结果。

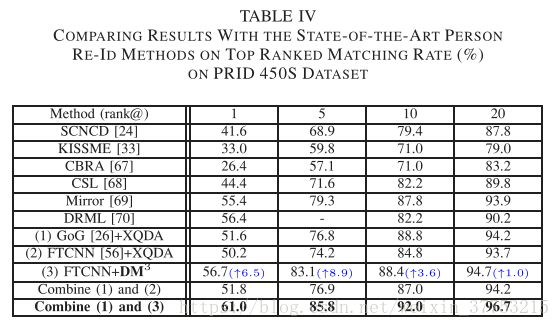
         2) PRID 450S Dataset: 根据在VIPeR数据集的评估过程，该数据集被随机分成两组。 一个用于训练（M = 225），另一个用于测试（N = 225）。 在训练集中，随机选择参考集Nr = 70。我们将我们的方法与以下方法进行比较：SCNCD [24]，KISSME [33]，基于颜色的排名聚合（CBRA）[67]，对应结构学习（CSL）[68]，镜像表示（Mirror）[69]， 和多样性正则化度量学习（DRML）[70]。 使用原始FTCNN描述符评估所提出的方法（DM^3）。 所有结果列于表IV中。 括号中的蓝色数字表示在给定FTCNN作为特征描述符的情况下，在每个等级处提出的DM^3相对于XQDA的改进。 表IV还显示融合结果（FTCNN + DM ^3和GoG + XQDA）优于其他方法产生的所有结果。

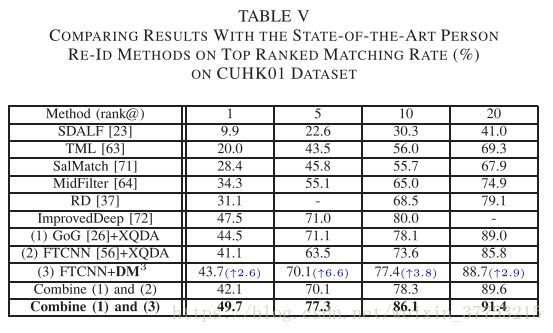
 3) CUHK01 Dataset：根据在VIPeR数据集的评估过程，该数据集被随机分成两组。 一个用于训练（M = 485），另一个用于测试（N = 486）。 在训练集中，随机选择参考集Nr = 100。 这些方法使用single-shot评估协议。 我们将我们的方法与以下方法进行比较：SDALF [23]，转移度量学习（TML）[63]，显著性匹配（SalMatch）[71]，MidFilter [64]，改进的深度学习架构（ImprovedDeep）[72]，以及 RD [37]。 使用原始FTCNN描述符评估所提出的方法（DM 3）。 所有结果都列在表V中。括号中的蓝色数字表示在给定FTCNN作为特征描述符的情况下，在每个等级处提出的DM 3相对于XQDA的改进。 表V还显示融合结果（FTCNN + DM 3和GoG + XQDA）优于其他方法生成的所有结果。

H. Evaluation on the Large Dataset

       众所周知，CUHK03 [27]和Market-1501 [73]是行人再识别任务中的两个大型数据集。 我们选择Market-1501数据集来评估我们的方法。 Market-1501数据集是目前行人再识别的最大基准数据集，与实际应用场景更为一致。 它包含32668个标记的1501个身份的边界框。 在[73]的实验设置之后，数据集被分成两部分：12936个具有751个用于训练的身份的图像和具有750个用于测试的身份的19732个图像。 在测试中，使用具有750个身份的3368个图像作为探针集合。

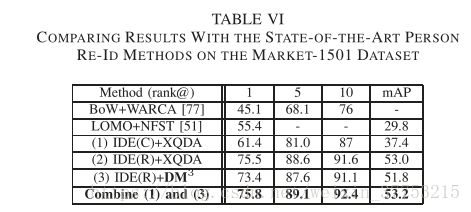
        为了与最先进的方法进行公平比较，我们从训练集中随机选择Nr = 100个图像对作为参考集。 [74]中提出的ID判别嵌入（IDE）特征被用作我们的基本特征。 IDE提取器在分类模型上得到有效训练，包括CaffeNet [75]和ResNet-50 [76]。 为了便于描述，我们将在CaffeNet和ResNet-50上训练的IDE分别缩写为IDE（C）和IDE（R）。 我们将我们的方法与以下方法进行比较。 具有加权近似秩分量分析方法（BoW + WARCA）的BoW特征[77]，具有零空间度量的LOMO描述符（LOMO + NFST）[51]，具有XQDA的IDE（C）特征以及具有IDE（R）特征的XQDA。 使用IDE（R）特征评估所提出的方法（DM^3）。 除了CMC值，我们还比较了平均精度（mAP），如[74]中所述。 我们报告此数据集的 single-query评估结果[73]。

         所有结果列于表VI中。 表VI显示融合结果（IDE（R）+ DM^3和IDE（C）+ XQDA）优于其他方法生成的所有结果。 但是，表VI还显示具有IDE（R）功能的建议方法（DM^3）的性能不如XQDA度量。 我们认为这是因为Market-1501数据集的人物图像是从六个不同的摄像头捕获的，而所提出的方法是在两个不同的摄像头下设计的。 在多相机条件下，我们的方法的优势在于可以抑制均匀的交叉相机成像变化。

 

I. Discussion on the Running Time

       在迭代过程中，离线训练的运行成本主要取决于梯度和损耗计算。 对于梯度，传统方法和提出的方法都使用矩阵操作来操作。 对于损失，传统的向量L2距离变换为矩阵F形距离。 使用MATLAB，这两个操作不会带来更多的时间损失。 但是，我们的方法使用了两个预测，这将使运行成本翻倍。 为了评估离线训练时间，我们以VIPeR数据集为例。 我们将训练集设置为M = 316，并且在训练集中，随机选择参考集Nr = 100。 四个部分梯度（10） - （13）的平均运行时间为0.10,0.11,0.36和0.39s。 要计算每个步骤的总损失，平均需要0.203秒。 为了减少迭代，使用自适应步长策略，这减少了很多时间。 它的平均成本仅为49.8秒。

      另一方面，每对差异矩阵的在线测试时间非常快。 使用（2），时间成本平均为0.0002秒。 总共测试N = 316组的成本为19.9秒。 另外，为了评估组合结果的测试时间，我们还应该考虑XQDA [25]方法，该方法试图从本质上学习马式距离度量。 在获得度量之后，通过马式距离计算向量的距离。 记录了N = 316测试组的平均测试时间为0.09秒。 也就是说，组合工作不会带来太多时间成本。

VI. CONCLUSION

        在本文中，我们提出了一种描述行人图像的新思路。 具体地，将特征描述从特征向量变换为差异矩阵，并且将距离度量从向量度量变换为矩阵度量。 我们通过与其他人的差异来识别人的模型类似于人类认知过程，并且它是有利的，因为所提出的描述可能减少了外部变化并且更精细。 公共数据集的实验结果证明了所提出的方法的有效性。 在下文中，我们还讨论了未来的研究方向。

       1）在我们提出的方法中，参考集是随机选择的，并且通过利用L2在参考集中稀疏地选择一些典型的人，这是在度量学习过程期间学习的。事实证明，这些选定的人比其他人更有价值。为此，我们可以研究哪些特征是有用的，以及应该利用多少人作为参考集。如果我们发现参考行人的选择机制，将在度量学习之前选择最有价值的参考人，并且通过删除稀疏术语，度量可能更具辨别力。
       2）我们通过构建手工制作的目标函数来提出矩阵度量学习方法。如我们所知，深度学习框架也可用于学习度量。例如，提出的判别项使用三重样本，其思想类似于三重网络[78]。
       3）尽管第V-I节显示组合工作不会带来太多时间成本，但计算差异矩阵的距离比计算特征向量的距离要花费更多时间。这激发了我们研究如何加速矩阵距离计算的过程。

REFERENCES

[1] Z. Wang et al., “Zero-shot person re-identification via cross-view
consistency,” IEEE Trans. Multimedia, vol. 18, no. 2, pp. 260–272,
Feb. 2016.
[2] A. J. Ma, J. Li, P. C. Yuen, and P. Li, “Cross-domain person reiden-
tification using domain adaptation ranking SVMs,” IEEE Trans. Image
Process., vol. 24, no. 5, pp. 1599–1613, May 2015.
[3] M. Ye et al., “Person reidentification via ranking aggregation of similar-
ity pulling and dissimilarity pushing,” IEEE Trans. Multimedia, vol. 18,
no. 12, pp. 2553–2566, Dec. 2016.
[4] Z. Wang et al., “Scale-adaptive low-resolution person re-identification
via learning a discriminating surface,” in Proc. Int. Joint Conf. Artif.
Intell., New York, NY, USA, 2016, pp. 2669–2675.
[5] S. Tan, F. Zheng, L. Liu, J. Han, and L. Shao, “Dense invari-
ant feature based support vector ranking for cross-camera person
re-identification,” IEEE Trans. Circuits Syst. Video Technol., to be
published, doi: 10.1109/TCSVT.2016.2555739.
[6] N. Martinel, G. L. Foresti, and C. Micheloni, “Person reidentification in
a distributed camera network framework,” IEEE Trans. Cybern., to be
published, doi: 10.1109/TCYB.2016.2568264.
[7] J. García et al., “Discriminant context information analysis for post-
ranking person re-identification,” IEEE Trans. Image Process., vol. 26,
no. 4, pp. 1650–1665, Apr. 2017.
[8] J. Chen, Y. Wang, J. Qin, L. Liu, and L. Shao, “Fast person re-
identification via cross-camera semantic binary transformation,” in Proc.
IEEE Conf. Comput. Vis. Pattern Recognit., 2017, pp. 3873–3882.
[9] J. Wang, Z. Wang, C. Liang, C. Gao, and N. Sang, “Equidistance
constrained metric learning for person re-identification,” Pattern
Recognit., vol. 74, pp. 38–51, Feb. 2018. [Online]. Available:
http://www.sciencedirect.com/science/article/pii/S0031320317303576
[10] M. Liu, H. Liu, and C. Chen, “Enhanced skeleton visualization for
view invariant human action recognition,” Pattern Recognit., vol. 68,
pp. 346–362, Aug. 2017.
[11] R. Hou, C. Chen, and M. Shah, “Tube convolutional neural network
(T-CNN) for action detection in videos,” CoRR, vol. abs/1703.10664,
2017. [Online]. Available: http://arxiv.org/abs/1703.10664
[12] B. Zhang et al., “Action recognition using 3D histograms of texture and
a multi-class boosting classifier,” IEEE Trans. Image Process., vol. 26,
no. 10, pp. 4648–4660, Oct. 2017.
[13] Z.-R. Lai, D.-Q. Dai, C.-X. Ren, and K.-K. Huang, “Discriminative
and compact coding for robust face recognition,” IEEE Trans. Cybern.,
vol. 45, no. 9, pp. 1900–1912, Sep. 2015.
[14] J. Ma, J. Zhao, Y. Ma, and J. Tian, “Non-rigid visible and infrared face
registration via regularized Gaussian fields criterion,” Pattern Recognit.,
vol. 48, no. 3, pp. 772–784, 2015.
[15] J. Jiang, J. Ma, C. Chen, X. Jiang, and Z. Wang, “Noise robust face
image super-resolution through smooth sparse representation,” IEEE
Trans. Cybern., to be published, doi: 10.1109/TCYB.2016.2594184.
[16] Y. Gao, J. Ma, and A. L. Yuille, “Semi-supervised sparse representa-
tion based classification for face recognition with insufficient labeled
samples,” IEEE Trans. Image Process., vol. 26, no. 5, pp. 2545–2560,
May 2017.
[17] M. Ding and G. Fan, “Multilayer joint gait-pose manifolds for
human gait motion modeling,” IEEE Trans. Cybern., vol. 45, no. 11,
pp. 2413–2424, Nov. 2015.
[18] D. Muramatsu, Y. Makihara, and Y. Yagi, “View transformation model
incorporating quality measures for cross-view gait recognition,” IEEE
Trans. Cybern., vol. 46, no. 7, pp. 1602–1615, Jul. 2016.
[19] W.-S. Zheng, S. Gong, and T. Xiang, “Person re-identification by proba-
bilistic relative distance comparison,” in Proc. IEEE Conf. Comput. Vis.
Pattern Recognit., Colorado Springs, CO, USA, 2011, pp. 649–656.
[20] J. Jiang, R. Hu, Z. Wang, Z. Han, and J. Ma, “Facial image hallucination
through coupled-layer neighbor embedding,” IEEE Trans. Circuits Syst.
Video Technol., vol. 26, no. 9, pp. 1674–1684, Sep. 2016.
[21] J. Jiang et al., “SRLSP: A face image super-resolution algorithm using
smooth regression with local structure prior,” IEEE Trans. Multimedia,
vol. 19, no. 1, pp. 27–40, Jan. 2017.
[22] D. Gray and H. Tao, “Viewpoint invariant pedestrian recognition with
an ensemble of localized features,” in Proc. Eur. Conf. Comput. Vis.,
2008, pp. 262–275.
[23] M. Farenzena, L. Bazzani, A. Perina, V. Murino, and M. Cristani,
“Person re-identification by symmetry-driven accumulation of local
features,” in Proc. IEEE Conf. Comput. Vis. Pattern Recognit.,
San Francisco, CA, USA, 2010, pp. 2360–2367.
[24] Y. Yang et al., “Salient color names for person re-identification,” in Proc.
Eur. Conf. Comput. Vis., 2014, pp. 536–551.
[25] S. Liao, Y. Hu, X. Zhu, and S. Z. Li, “Person re-identification by
local maximal occurrence representation and metric learning,” in Proc.
IEEE Conf. Comput. Vis. Pattern Recognit., Boston, MA, USA, 2015,
pp. 2197–2206.
[26] T. Matsukawa, T. Okabe, E. Suzuki, and Y. Sato, “Hierarchical Gaussian
descriptor for person re-identification,” in Proc. IEEE Conf. Comput. Vis.
Pattern Recognit., Las Vegas, NV, USA, 2016, pp. 1363–1372.
[27] W. Li, R. Zhao, T. Xiao, and X. Wang, “DeepReID: Deep filter
pairing neural network for person re-identification,” in Proc. IEEE
Conf. Comput. Vis. Pattern Recognit., Columbus, OH, USA, 2014,
pp. 152–159.
[28] S. Ding, L. Lin, G. Wang, and H. Chao, “Deep feature learning with rela-
tive distance comparison for person re-identification,” Pattern Recognit.,
vol. 48, no. 10, pp. 2993–3003, 2015.
[29] R. Zhang, L. Lin, R. Zhang, W. Zuo, and L. Zhang, “Bit-scalable deep
hashing with regularized similarity learning for image retrieval and per-
son re-identification,” IEEE Trans. Image Process., vol. 24, no. 12,
pp. 4766–4779, Dec. 2015.
[30] J. Wang, Z. Wang, C. Gao, and N. Sang, “DeepList: Learning deep
features with adaptive listwise constraint for person reidentification,”
IEEE Trans. Circuits Syst. Video Technol., vol. 27, no. 3, pp. 513–524,
Mar. 2017.
[31] F. Zhu, X. Kong, Z. Liang, H. Fu, and Q. Tian, “Part-based deep hashing
for large-scale person re-identification,” IEEE Trans. Image Process.,
vol. 26, no. 10, pp. 4806–4817, Oct. 2017.
[32] L. Zheng, Y. Yang, and Q. Tian, “SIFT meets CNN: A decade survey
of instance retrieval,” IEEE Trans. Pattern Anal. Mach. Intell., to be
published, doi: 10.1109/TPAMI.2017.2709749.
[33] M. Köstinger, M. Hirzer, P. Wohlhart, P. M. Roth, and H. Bischof,
“Large scale metric learning from equivalence constraints,” in Proc.
IEEE Conf. Comput. Vis. Pattern Recognit., Providence, RI, USA, 2012,
pp. 2288–2295.

[34] Z. Li et al., “Learning locally-adaptive decision functions for person ver-
ification,” in Proc. IEEE Conf. Comput. Vis. Pattern Recognit., Portland,
OR, USA, 2013, pp. 3610–3617.
[35] S. Pedagadi, J. Orwell, S. Velastin, and B. Boghossian, “Local Fisher
discriminant analysis for pedestrian re-identification,” in Proc. IEEE
Conf. Comput. Vis. Pattern Recognit., Portland, OR, USA, 2013,
pp. 3318–3325.
[36] L. Zheng, S. Duffner, K. Idrissi, C. Garcia, and A. Baskurt, “Pairwise
identity verification via linear concentrative metric learning,” IEEE
Trans. Cybern., to be published, doi: 10.1109/TCYB.2016.2634011.
[37] L. An, M. Kafai, S. Yang, and B. Bhanu, “Person reidentification with
reference descriptor,” IEEE Trans. Circuits Syst. Video Technol., vol. 26,
no. 4, pp. 776–787, Apr. 2016.
[38] X. Wang, G. Doretto, T. Sebastian, J. Rittscher, and P. Tu, “Shape and
appearance context modeling,” in Proc. IEEE Int. Conf. Comput. Vis.,
Rio de Janeiro, Brazil, 2007, pp. 1–8.
[39] B. Ma, Y. Su, and F. Jurie, “BiCov: A novel image representation for
person re-identification and face verification,” in Proc. Brit. Mach. Vis.
Conf., Surrey, U.K., 2012, pp. 1–11.
[40] R. Layne, T. M. Hospedales, and S. Gong, “Person re-identification by
attributes,” in Proc. Brit. Mach. Vis. Conf., vol. 2. Surrey, U.K., 2012,
pp. 1–11.
[41] I. Kviatkovsky, A. Adam, and E. Rivlin, “Color invariants for person
reidentification,” IEEE Trans. Pattern Anal. Mach. Intell., vol. 35, no. 7,
pp. 1622–1634, Jul. 2013.
[42] R. Zhao, W. Ouyang, and X. Wang, “Unsupervised salience learning
for person re-identification,” in Proc. IEEE Conf. Comput. Vis. Pattern
Recognit., Portland, OR, USA, 2013, pp. 3586–3593.
[43] V. Eiselein, G. Sternharz, T. Senst, I. Keller, and T. Sikora, “Person re-
identification using region covariance in a multi-feature approach,” in
Proc. Int. Conf. Image Anal. Recognit., 2014, pp. 77–84.
[44] H. Bay, A. Ess, T. Tuytelaars, and L. Van Gool, “Speeded-up robust
features (SURF),” Comput. Vis. Image Understand., vol. 110, no. 3,
pp. 346–359, 2008.
[45] M. Hirzer, C. Beleznai, M. Köstinger, P. M. Roth, and H. Bischof,
“Dense appearance modeling and efficient learning of camera transi-
tions for person re-identification,” in Proc. Int. Conf. Image Process.,
Orlando, FL, USA, 2012, pp. 1617–1620.
[46] M. Dikmen, E. Akbas, T. S. Huang, and N. Ahuja, “Pedestrian recog-
nition with a learned metric,” in Proc. Asian Conf. Comput. Vis., 2010,
pp. 501–512.
[47] K. Q. Weinberger and L. K. Saul, “Distance metric learning for large
margin nearest neighbor classification,” J. Mach. Learn. Res., vol. 10,
pp. 207–244, Dec. 2009.
[48] D. Tao, L. Jin, Y. Wang, Y. Yuan, and X. Li, “Person re-identification
by regularized smoothing KISS metric learning,” IEEE Trans. Circuits
Syst. Video Technol., vol. 23, no. 10, pp. 1675–1685, Oct. 2013.
[49] A. Mignon and F. Jurie, “PCCA: A new approach for distance learning
from sparse pairwise constraints,” in Proc. IEEE Conf. Comput. Vis.
Pattern Recognit., Providence, RI, USA, 2012, pp. 2666–2672.
[50] Y. Wang, R. Hu, C. Liang, C. Zhang, and Q. Leng, “Camera com-
pensation using a feature projection matrix for person reidentification,”
IEEE Trans. Circuits Syst. Video Technol., vol. 24, no. 8, pp. 1350–1361,
Aug. 2014.
[51] L. Zhang, T. Xiang, and S. Gong, “Learning a discriminative null space
for person re-identification,” in Proc. IEEE Conf. Comput. Vis. Pattern
Recognit., Las Vegas, NV, USA, 2016, pp. 1239–1248.
[52] F. Zheng and L. Shao, “Learning cross-view binary identities for fast
person re-identification,” in Proc. Int. Joint Conf. Artif. Intell., New York,
NY, USA, 2016, pp. 2399–2406.
[53] L. An, X. Chen, S. Yang, and X. Li, “Person re-identification by
multi-hypergraph fusion,” IEEE Trans. Neural Netw. Learn. Syst., to
be published, doi: 10.1109/TNNLS.2016.2602082.
[54] L. Yang, X. Cao, D. Jin, X. Wang, and D. Meng, “A unified semi-
supervised community detection framework using latent space graph
regularization,” IEEE Trans. Cybern., vol. 45, no. 11, pp. 2585–2598,
Nov. 2015.
[55] D. Gray, S. Brennan, and H. Tao, “Evaluating appearance models for
recognition, reacquisition, and tracking,” in Proc. IEEE Int. Workshop
Perform. Eval. Tracking Surveillance, vol. 3. 2007, pp. 1–7.
[56] T. Matsukawa and E. Suzuki, “Person re-identification using CNN fea-
tures learned from combination of attributes,” in Proc. Int. Conf. Pattern
Recognit., Cancún, Mexico, 2016, pp. 2428–2433.
[57] J. Ma, J. Zhao, J. Tian, X. Bai, and Z. Tu, “Regularized vector field learn-
ing with sparse approximation for mismatch removal,” Pattern Recognit.,
vol. 46, no. 12, pp. 3519–3532, 2013.
[58] F. Nie, H. Huang, X. Cai, and C. H. Ding, “Efficient and robust feature
selection via joint l2, 1-norms minimization,” in Proc. Adv. Neural Inf.
Process. Syst., Vancouver, BC, Canada, 2010, pp. 1813–1821.
[59] J. Ma, C. Chen, C. Li, and J. Huang, “Infrared and visible image
fusion via gradient transfer and total variation minimization,” Inf. Fusion,
vol. 31, pp. 100–109, Sep. 2016.
[60] Y. Sun, X. Tao, Y. Li, and J. H. Lu, “Robust two-dimensional principal
component analysis via alternating optimization,” in Proc. Int. Conf.
Image Process., Melbourne, VIC, Australia, 2013, pp. 340–344.
[61] C.-J. Lin, “Projected gradient methods for nonnegative matrix factoriza-
tion,” Neural Comput., vol. 19, no. 10, pp. 2756–2779, 2007.
[62] P. M. Roth, M. Hirzer, M. Köestinger, C. Beleznai, and H. Bischof,
“Mahalanobis distance learning for person re-identification,” in Person
Re-Identification. London, U.K.: Springer, 2014, pp. 247–267.
[63] W. Li, R. Zhao, and X. Wang, “Human reidentification with transferred
metric learning,” in Proc. Asian Conf. Comp. Vis., 2012, pp. 31–44.
[64] R. Zhao, W. Ouyang, and X. Wang, “Learning mid-level filters for person
re-identification,” in Proc. IEEE Conf. Comput. Vis. Pattern Recognit.,
Columbus, OH, USA, 2014, pp. 144–151.
[65] D. Yi, Z. Lei, S. Liao, and S. Z. Li, “Deep metric learning for person
re-identification,” in Proc. Int. Conf. Pattern Recognit., 2014, pp. 34–39.
[66] S.-Z. Chen, C.-C. Guo, and J.-H. Lai, “Deep ranking for person re-
identification via joint representation learning,” IEEE Trans. Image
Process., vol. 25, no. 5, pp. 2353–2367, May 2016.
[67] R. F. D. C. Prates and W. R. Schwartz, “CBRA: Color-based rank-
ing aggregation for person re-identification,” in Proc. Int. Conf. Image
Process., Quebec City, QC, Canada, 2015, pp. 1975–1979.
[68] Y. Shen et al., “Person re-identification with correspondence structure
learning,” in Proc. IEEE Int. Conf. Comput. Vis. (ICCV), Santiago, Chile,
2015, pp. 3200–3208.
[69] Y.-C. Chen, W.-S. Zheng, and J. Lai, “Mirror representation for modeling
view-specific transform in person re-identification,” in Proc. Int. Joint
Conf. Artif. Intell., Buenos Aires, Argentina, 2015, pp. 3402–3408.
[70] W. Yao, Z. Weng, and Y. Zhu, “Diversity regularized metric learning for
person re-identification,” in Proc. Int. Conf. Image Process., Phoenix,
AZ, USA, 2016, pp. 4264–4268.
[71] R. Zhao, W. Ouyang, and X. Wang, “Person re-identification by salience
matching,” in Proc. IEEE Int. Conf. Comput. Vis., Sydney, NSW,
Australia, 2013, pp. 2528–2535.
[72] E. Ahmed, M. Jones, and T. K. Marks, “An improved deep learning
architecture for person re-identification,” in Proc. IEEE Conf. Comput.
Vis. Pattern Recognit., Boston, MA, USA, 2015, pp. 3908–3916.
[73] L. Zheng et al., “Scalable person re-identification: A benchmark,”
in Proc. IEEE Int. Conf. Comput. Vis., Santiago, Chile, 2015,
pp. 1116–1124.
[74] L. Zheng, Y. Yang, and A. G. Hauptmann, “Person re-identification:
Past, present and future,” CoRR, vol. abs/1610.02984, 2016. [Online].
Available: http://arxiv.org/abs/1610.02984
[75] A. Krizhevsky, I. Sutskever, and G. E. Hinton, “ImageNet classifica-
tion with deep convolutional neural networks,” in Proc. Adv. Neural Inf.
Process. Syst., 2012, pp. 1097–1105.
[76] K. He, X. Zhang, S. Ren, and J. Sun, “Deep residual learning for
image recognition,” in Proc. IEEE Conf. Comput. Vis. Pattern Recognit.,
Las Vegas, NV, USA, 2016, pp. 770–778.
[77] C. Jose and F. Fleuret, “Scalable metric learning via weighted approx-
imate rank component analysis,” in Proc. Eur. Conf. Comput. Vis.,
Amsterdam, The Netherlands, 2016, pp. 875–890.
[78] E. Hoffer and N. Ailon, “Deep metric learning using triplet network,”
in Proc. Int. Workshop Similarity Based Pattern Recognit., 2015,
pp. 84–92.