遗传算法解决旅行商问题

遗传算法解决旅行商问题

学号：23020201153794

系别：计算机科学系

课程名称：计算智能

一、问题描述

旅行商问题（Travelling Salesman Problem, 简记TSP，亦称货郎担问题)：设有n个城市和距离矩阵D=[dij]，其中dij表示城市i到城市j的距离，i，j=1，2 … n，则问题是要找出遍访每个城市恰好一次的一条回路并使其路径长度为最短。

二、问题分析

1.对TSP的分析

旅行商问题属于所谓的NP完全问题。精确的解决TSP只能通过穷举所有的路径组合，其时间复杂度是O(N!) 。而使用遗传算法则可以较快速算法一条近似的最优路径。
TSP的一个解可表述为一个循环排列
π= (π1， π2， π3 … πn），即 π1 → π2 → … → πn → π1。 有（n-1）！/2 种不同方案，若使用穷举法，当n很大时计算量是不可接受的。旅行商问题综合了一大类组合优化问题的典型特征，属于NP难题，不能在多项式时间内进行检验。若使用动态规划的方法时间复杂性和空间复杂性都保持为n的指数函数。

2.遗传算法GA

（1）GA简介

遗传算法（Genetic Algorithm, GA）是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型，是一种通过模拟自然进化过程搜索最优解的方法。
其主要特点是直接对结构对象进行操作，不存在求导和函数连续性的限定；具有内在的隐并行性和更好的全局寻优能力；采用概率化的寻优方法，不需要确定的规则就能自动获取和指导优化的搜索空间，自适应地调整搜索方向。

遗传算法以一种群体中的所有个体为对象，并利用随机化技术指导对一个被编码的参数空间进行高效搜索。其中，选择、交叉和变异构成了遗传算法的遗传操作；参数编码、初始群体的设定、适应度函数的设计、遗传操作设计、控制参数设定五个要素组成了遗传算法的核心内容。

（2）GA过程

遗传算法是从代表问题可能潜在的解集的一个种群（population）开始的，而一个种群则由经过基因（gene）编码的一定数目的个体(individual)组成。每个个体实际上是染色体(chromosome)带有特征的实体。

染色体作为遗传物质的主要载体，即多个基因的集合，其内部表现（即基因型）是某种基因组合，它决定了个体的形状的外部表现，如黑头发的特征是由染色体中控制这一特征的某种基因组合决定的。因此，在一开始需要实现从表现型到基因型的映射即编码工作。由于仿照基因编码的工作很复杂，我们往往进行简化，如二进制编码。

初代种群产生之后，按照适者生存和优胜劣汰的原理，逐代（generation）演化产生出越来越好的近似解，在每一代，根据问题域中个体的适应度（fitness）大小选择（selection）个体，并借助于自然遗传学的遗传算子（genetic operators）进行组合交叉（crossover）和变异（mutation），产生出代表新的解集的种群。

这个过程将导致种群像自然进化一样的后生代种群比前代更加适应于环境，末代种群中的最优个体经过解码（decoding），可以作为问题近似最优解。

（3）GA描述

步Ⅰ：初始化
步 II：Ⅱ种群进化

（4）GA一般流程

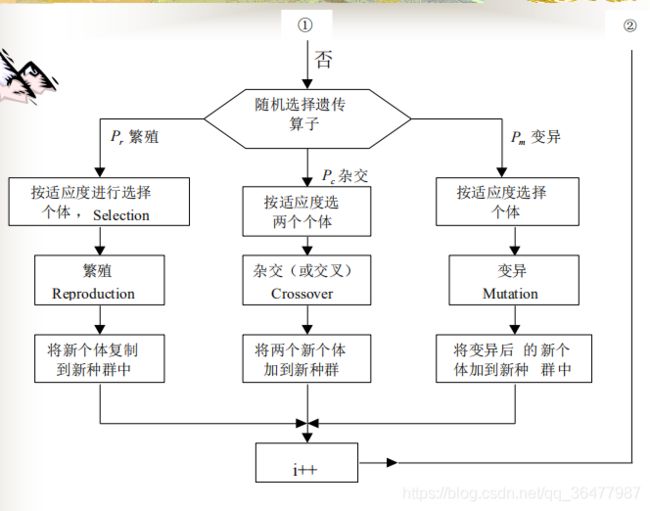
（5）常规遗传算法（GA）的流程图

三、算法设计

1.源代码

import numpy as np
import matplotlib.pyplot as plt

'''
适应度函数，计算每个排列的适应度，并保存到pop矩阵第二维的最后一项
'''
def fitness(pop, num, city_num, x_position_add_end, y_position_add_end):
    for x1 in range(num):
        square_sum = 0
        for x2 in range(city_num):
            square_sum += (x_position_add_end[int(pop[x1][x2])] - x_position_add_end[int(pop[x1][x2+1])])**2 + (y_position_add_end[int(pop[x1][x2])] - y_position_add_end[int(pop[x1][x2+1])])**2
        # print(round(1/np.sqrt(square_sum),7))
        pop[x1][-1] = round(1/np.sqrt(square_sum),7)

'''
方法：比如A当前种群中的最优解，B为经过交叉、变异后的最差解，把A作为最当前代中的最优解保存下来作为这一代的最优解，同时A也参与交叉
和变异。经过交叉、变异后的最差解为B，那么我再用A替代B。
:argument pop矩阵
:return 本代适应度最低的个体的索引值和本代适应度最高的个体
'''
def choiceFuction(pop):
    yield np.argmin(pop[:, -1])
    yield pop[np.argmax(pop[:, -1])]


def choice(pop, num, city_num, x_end, y_end, b):
    fitness(pop, num, city_num, x_end, y_end)
    c,d =choiceFuction(pop)
    # 上一代的最优值替代本代中的最差值
    pop[c] = b
    return pop


def drawPic(maxFitness, x, y, i):
    index = np.array(maxFitness[:-1],dtype=np.int32)
    x_position_add_end = np.append(x[index], x[[index[0]]])
    y_position_add_end = np.append(y[index], y[[index[0]]])
    fig = plt.figure()
    plt.plot(x_position_add_end,y_position_add_end,'-o')
    plt.xlabel('x',fontsize = 16)
    plt.ylabel('y',fontsize = 16)
    plt.title('{iter}'.format(iter=i))
    plt.show()

'''
杂交
'''
def matuing(pop, pc, city_num, pm, num):
    mating_matrix = np.array(1 - (np.random.rand(num) > pc), dtype=np.bool)  # 交配矩阵，如果为true则进行交配
    a = list(pop[mating_matrix][:, :-1])  # 进行交配的个体
    b = list(pop[np.array(1 - mating_matrix, dtype=bool)][:, :-1])  # 未进行交配的个体,直接放到下一代
    b = [list(i) for i in b]  # 对b进行类型转换，避免下面numpy.array 没有index属性
    #     print(a)
    if len(a) % 2 != 0:
        b.append(a.pop())
    #     print('ab的长度：',len(a),len(b))
    for i in range(int(len(a) / 2)):
        # 随机初始化两个交配点,这里写得不好，这边的两个点初始化都是一个在中间位置偏左，一个在中间位置偏右
        p1 = np.random.randint(1, int(city_num / 2) + 1)
        p2 = np.random.randint(int(city_num / 2) + 1, city_num)
        x1 = list(a.pop())
        x2 = list(a.pop())
        matuting(x1, x2, p1, p2)
        # 交配之后产生的个体进行一定概率上的变异
        variation(x1, pm, city_num)
        variation(x2, pm, city_num)
        b.append(x1)
        b.append(x2)
    zero = np.zeros((num, 1))
    #     print('b的形状：',len(b))
    temp = np.column_stack((b, zero))
    return temp


def matuting(x1, x2, p1, p2):
    # 以下进行交配
    # 左边交换位置
    temp = x1[:p1]
    x1[:p1] = x2[:p1]
    x2[:p1] = temp
    # 右边交换位置
    temp = x1[p2:]
    x1[p2:] = x2[p2:]
    x2[p2:] = temp
    # 寻找重复的元素
    center1 = x1[p1:p2]
    center2 = x2[p1:p2]
    while True:  # x1左边
        for i in x1[:p1]:
            if i in center1:
                # print(center1.index(i)) # 根据值找到索引
                x1[x1[:p1].index(i)] = center2[center1.index(i)]
                break
        if np.intersect1d(x1[:p1], center1).size == 0:  # 如果不存在交集，则循环结束
            break
    while True:  # x1右边
        for i in x1[p2:]:
            if i in center1:
                # print(center1.index(i)) # 根据值找到索引
                x1[x1[p2:].index(i) + p2] = center2[center1.index(i)]
                # print(x1)
                break
        if np.intersect1d(x1[p2:], center1).size == 0:  # 如果不存在交集，则循环结束
            break
    while True:  # x2左边
        for i in x2[:p1]:
            if i in center2:
                #                     print(center2.index(i)) # 根据值找到索引
                x2[x2[:p1].index(i)] = center1[center2.index(i)]
                break
        if np.intersect1d(x2[:p1], center2).size == 0:  # 如果不存在交集，则循环结束
            break
    while True:  # x2右边
        for i in x2[p2:]:
            if i in center2:
                # print(center2.index(i)) # 根据值找到索引
                x2[x2[p2:].index(i) + p2] = center1[center2.index(i)]
                # print(x2)
                break
        if np.intersect1d(x2[p2:], center2).size == 0:  # 如果不存在交集，则循环结束
            break

'''
变异
'''
def variation(list_a, pm, city_num):

    if np.random.rand() < pm:
        p1 = np.random.randint(1, int(city_num / 2) + 1)
        p2 = np.random.randint(int(city_num / 2) + 1, city_num)
        #         print(p1,p2)
        temp = list_a[p1:p2]
        temp.reverse()
        list_a[p1:p2] = temp
#         print(list_a)

if __name__ == '__main__':
    # 初始化
    stack = []  # 存放访问顺序和每个个体适应度
    n = 250  # 初始化群体的数目
    city_num = 10  # 城市数目
    pc = 0.9  # 每个个体的交配概率
    pm = 0.2  # 每个个体的变异概率
    x = np.random.randint(0, 100, size=city_num)
    y = np.random.randint(0, 100, size=city_num)
    x_end = np.append(x, x[0])
    y_end = np.append(y, y[0])
    for i in range(n):
        stack.append(np.random.permutation(np.arange(0, city_num)))  # 假设有5个城市，初始群体的数目为60个
        # 初始化化一个60*1的拼接矩阵，值为0
    zero = np.zeros((n, 1))
    stack = np.column_stack((stack, zero))  # 矩阵的拼接
    fitness(stack, n, city_num, x_end, y_end)
    for i in range(180):
        a, b = choiceFuction(stack)  # a 为当代适应度最小的个体的索引，b为当代适应度最大的个体,这边要保留的是b
        #         print('索引值和适应度最大的个体：',a,b)
        #     pop[a]=b
        if (i + 1) % 10 == 0:
            drawPic(b, x, y, i + 1)  # 根据本代中的适应度最大的个体画图
        pop_temp = matuing(stack, pc, city_num, pm, n)  # 交配变异
        stack = choice(pop_temp, n, city_num, x_end, y_end, b)

2.运行结果

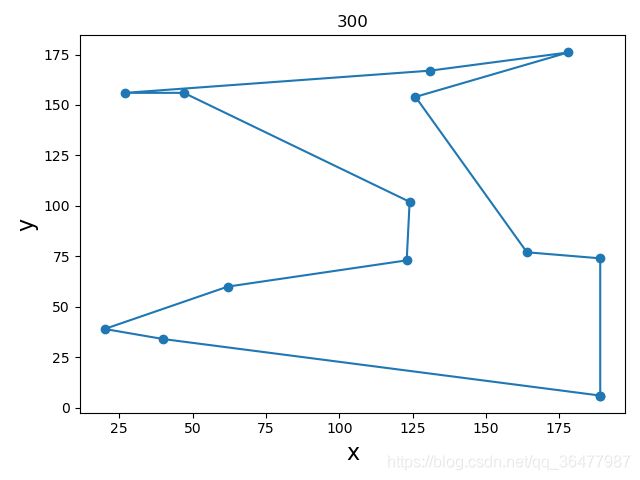
采用python实现GA的TSP算法，设置城市的个数为13，每个城市坐标在0~200随机生成，迭代300次，3次运行结果如下。

（1）结果1

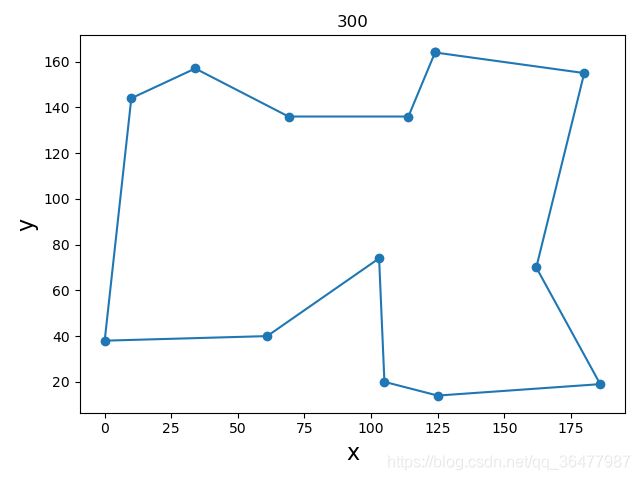
（2）结果2

（3）结果3

四、心得体会

1.遗传算法主要包括初始种群的产生（编码），适应度函数的确定，遗传算子（选择、交叉、变异）。
2.遗传算法(Genetic Algorithms, GA)是一类借鉴生物界自然选择和自然遗传机制的随机化搜索最优解的算法。
它模拟自然选择和自然遗传过程中发生的繁殖、交叉和基因突变现象，在每次迭代中都保留一组候选解，并按某种指标从解群中选取较优的个体，利用遗传算子(选择、交叉和变异)对这些个体进行组合，产生新一代的候选解群，重复此过程，直到满足某种收敛指标为止。