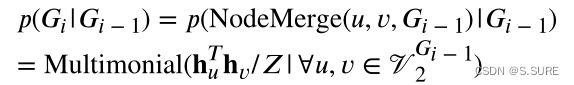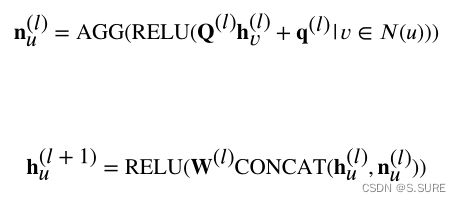G2SAT: Learning to Generate SAT Formulas论文精读

0. Abstract

        SAT（布尔可满足）问题被证明是一个经典的np完全问题，作为一个计算机科学的基本问题，在决策、验证和理论证明等很多方面都有应用。目前的SAT求解器的开发和评估依赖于现有的有限的现实问题，且现有的手工制作的公式由于人类/专家的知识局限性，无法全面地捕获一个SAT实例所具有的广泛特征。这篇文章所提出的G2SAT框架以一组公式为输入，学习SAT公式的生成。文章使用二部图的表示形式对SAT公式进行建模，以图和SAT求解器两种度量展示了其生成的SAT公式的现实的SAT实例的相似性。更重要的是，使用其生成的SAT公式，能够提升现有SAT求解器的求解性能。

1. Introducation

        首先还是对SAT问题的一个背景介绍，说明其作为一个np完全问题，在之前被认为不存在一个统一的方法进行求解。然而随着其在实践上的发展，大规模的SAT问题实例可以被很好地解决，且有一些特定的算法在特定SAT问题上的求解更加高效。例如像WalkSAT这样的不完全搜索策略以及survey propagation等方法对于随机生成的大型SAT问题的求解上具有高效的性能，而使用CDCL的完全搜索策略则在真实的工业环境中的SAT问题的求解更高效。

        接下来讲了SAT公式生成的任务在当前环境下的限制，且伪工业的SAT公式生成被列为了命题推理和搜索的十大关键挑战之一。而对于该问题的解决方法之一，是将原始的公式生成问题重新定义为一个图生成任务。通过一个双射，任意的SAT实例都可以被转化成一个二分图的结构，被称为literal-clause graph（LCG）。先前的手工方法，随着更多的真实SAT实例被发现，其局限性被暴露出来，主要表现为对问题实例的信息捕获能力上的不足。而近年来图生成模型在社交网络、引用关系网络以及化学生物等领域表现出的出色能力给我们提供了一种新的思路。但是由于这些模型没有在二分图方面的限制，所以不能直接运用在该问题上，而后处理的策略也意味着更高的成本，还会丢失掉二部图所具有的一些性质。

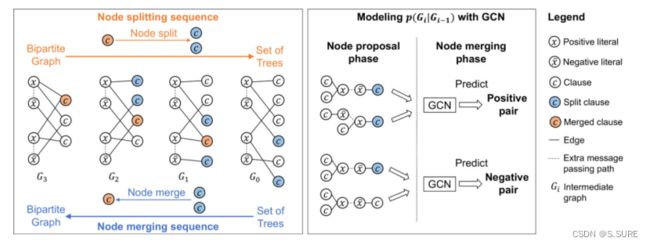
        G2SAT作为第一个基于一系列给定公式生成SAT公式的深度生成模型，使用LCG将SAT公式建模为一个二分图生成问题，以下图为例，二分图左边的节点为SAT公式中的变量，右边的节点为SAT公式中的子句（对变量的约束）。任意一个二分图的生成可以看作从一系列的树结构为开始，使用一系列的节点合并操作，在节点合并的同时，树也被合并，从而形成一个二分图。如下图左图所示，从左到右为节点的分割过程，从右到左为节点的合并过程，例如，G3中的橙色节点，在G2种被分割为两个蓝色节点，反之同理。假设我们学习这个合并序列，就可以以一系列的树为起点，以迭代的方式完成真实SAT实例的二分图的构造。这样的每一个迭代步骤作为GCN的一个样本，在每一个迭代中，GCN的权重共享。

        在上述思路之下，需要考虑如何在只给定静态输入的SAT公式的情况下设计一个顺序生成的过程，即怎样为生成器提供训练样本。如上图左图所示，节点的分割过程可以看作是节点合并的逆过程，因此可以对给定的二分图（真实的SAT实例）执行节点切分的过程，将其分割为一系列的树，然后再反向执行该过程，就实现了一个顺序生成二分图的流程（这样一个正难则反的思路在许多情况下是十分有效的，例如矩阵乘法的张量分解等）。本文训练一个GCN为基础的分类器基于目前生成的图来决定在下一次迭代中，对哪两个节点进行合并。

        在每次迭代中，模型的运行分为两步，第一步随机选择候选节点对，第二步为节点合并阶段，GCN被用于选择最有可能的两个节点执行合并。这样的迭代过程从使用一系列树初始化模型开始，一直到一个用户定义的停止条件结束。

        接下来文章说明了实验结果所表明的模型的优越性，即其在许多具有图特性的SAT实例的SAT公式生成任务上能生成比现有最SOTA的模型更低的误差。且其生成的公式具有与真实SAT实例的公式相同的硬度特性，这是说，对于模型生成的公式，那些用于求解真实SAT问题的求解器表现出的性能要优于解决随机生成的SAT问题的求解器。并且，使用G2SAT生成的公式还可以指导SAT求解器的超参数优化，从而实现更高的性能（更快的求解速度）。

2. Preliminaries

SAT公式生成的目标

        设计一个SAT公式的生成器，输入一系列的SAT公式，生成一个与输入公式具有相似属性的新的SAT公式。这个生成的公式不仅要捕获该SAT实例的图理论的属性，还应捕获其实际的SAT求解器行为的属性。对于这个行为的解释为：对于输入为来自于某个应用领域的公式X，解决该领域SAT实例的求解器也要擅长于求解G2SAT由此生成的SAT公式。

SAT公式和其图表示

        SAT公式由一系列的变量和逻辑运算连接词（与、或、非）构成，当存在一组变量赋值使得整个SAT公式的真值为真时，我们认为该SAT公式对应的问题是可满足的。本文中的SAT公式表示形式为合取范式（CNF），如(x1∨x2∨¬x3)∧(¬x1∨¬x2)，CNF由一系列的子句所构成，子句之间通过与运算连接，每一个子句内部的变量通过或运算连接（因此，一个CNF要为真，要求每个子句的真值为真；而一个子句的真值要为真，只需要其中的任意一个变量的真值为真，这一点是由与运算和或运算的性质所决定的）。对于一个CNF的图表示，文中提到了四种方式：1）字面量-子句图（LCG）：每个字面量和每个CNF子句被表示为一个节点，节点之间的边表示了某个字面量是否在某个子句中出现。边只在变量节点和子句节点之间连接，因此LCG是一个二分图的结构，存在一个LCG到CNF公式的双射。2）Literal-Incidence Graph（LIG）：每个变量被表示为一个节点，当两个变量同时出现在一个子句中时，二者对应的节点之间连起一条边。3）变量-子句图（VCG）：大致与LCG相同，只是对每个变量以及它的非合并为一个图节点。4）Variable-Incidence Graph （VIG）：其与LIG的关系同VCG与LCG的关系。文章使用LCG实现SAT公式的图表示。

        对于具体的二分图的表示策略，文中给了一段描述，如下图所示：

        简而言之，就是对LCG的二分图表示给出了一个规定，把节点集合分为两个部分V1和V2，V1表示为字面量对应的节点集合，V2表示为SAT公式中的子句对应的节点集合，这样就将LCG分成了两个部分，任何一条边都要建立在V1和V2之间，表示变量在子句中的出现与否。 

使用LCG生成SAT公式的优势

        LCG与SAT公式之间具有双射关系。这个特性虽然在LIG中也有，但是LIG不显式体现对变量的约束，这虽然使得其生成较LCG更为简单，但是在SAT公式转换为LIG时，子句和变量之间的约束关系会丢失，因为LIG只表示了两个变量之间是否出现在同一个CNF子句中，但是不能体现它们共现了多少次，每一次共现发生在哪个子句中。这样的模糊性，导致了一个LIG会对应多个不同的CNF，从我个人看来，这样的一个模糊性导致了从一个CNF公式转化为LIG是容易的，但是逆过程就可能会对应不一样的结果。

3. Rekated Work

SAT生成器

        这里是对现有的SAT生成器的一个简单介绍，说明了现有的SAT生成器多是手工制作的用于生成符合特定图统计的公式，并罗列了主流的生成伪工业SAT实例的生成器以及用于生成随机SAT实例的SAT生成器。

深度图生成器

        现有的深度图生成器主要分为两类：第一类模型通过直接解码计算节点嵌入或潜变量，或者学习图的随机游走分布，来生成给定图的perturbations（摄动？）；第二类模型学习依次添加节点和边来完成图的生成。还有特定领域的专注于分子结构图和3D点云图的模型。但是现有的模型还是不能直接用于SAT公式图的生成，因此本文提出了一种新的二分图生成器，其遵循SAT公式的图表示施加的所有约束，通过一系列的节点合并操作生成SAT公式对应的二分图。

用在SAT的深度学习

        NeuroSAT也使用图表示SAT公式并且使用GCN计算节点嵌入。而NeuroSAT专注于SAT公式的求解，而本文的模型专注于SAT公示的生成。本文工作的初步版本用于根据现有的图生成模型学习SAT公式对应的LIG的生成。但是从生成LIG提取SAT公式需要大量的后处理（我在前文中也有提到这个逆过程）。本文提出的深度图生成模型直接学习SAT公式和LCG之间的双射关系，从而更好地捕获SAT公式的特性。

4. G2SAT框架

4.1 G2SAT：通过迭代节点合并操作生成二分图

        每一个具有不同节点数目和边数目的二分图，从图的角度上直观地反映了一个SAT公式的复杂程度，对于一个SAT公式对应的二分图而言，直接学习它的数据分布是比较困难的。因此G2SAT使用一步步的迭代生成策略，对二分图的数据分布P(G)进行学习。其公式为：

        Gi表示迭代到第i步时的二分图（在第一张图的左侧有所展示）。对于二分图的生成，本文不关注其迭代轨迹，只要生成的二分图相同即可。这个假设说明了该任务具有的马尔可夫性质，即当前状态只取决于前一个或前几个状态，而与更之前的状态无关，这个条件假设定义为下面的公式：

        对于p(Gi|Gi-1) 的建模，先前的方法多是将其建模为随机添加节点或者边到Gi-1上来生成Gi的分布。但是这样的建模方式会导致任何形式的图的生成，而丧失了二分图特有的一些性质，而G2SAT将其建模为节点的拆分和合并操作，不仅保留了二分图本身的限制，还省去了人工规则的使用以及对普通图后处理成二分图的操作（保证了生成的图一定是二分图）。

定义1：节点的拆分和合并

        如上文所讲的那样，更细致地，对于节点v的拆分，先添加新节点v'，将v和其邻居节点的边中的一部分连接到v'；反之，对于节点u和v的合并操作，将v与其邻居节点之间的边全部连接到u节点，并将v节点删除。文中给出了一个形式化的表述。

发现1：二分图可以通过将一边的节点执行拆分操作得到一系列的树

        首先是对这个发现的简单证明，节点的拆分操作意味着一个节点度的减少，对一个二分图的一侧节点不断进行拆分，会使得这一侧的节点的度逐渐都变为1，从而成为树的叶子节点，另一侧不被处理的节点则成为这一系列树的根节点。同样地，执行这一系列节点拆分的逆过程，就可以还原原来的二分图。G2SAT则是对CNF子句所对应的节点执行合并完成二分图的构造。其公式为：

         hu和hv是节点u和v对应的嵌入表示，Z是一个归一化参数，用来保证这个分布是合法的。对于u的嵌入表示，要求能够捕获到u的多跳邻居结构（这个结构我认为是在合并过程中合并到u的所有v节点的邻居节点）。G2SAT使用GraphSAGE框架进行节点嵌入的计算，这是一个GCN的变体，已经被证明在不同的图中有很强的归纳学习能力。单层的GraphSAGE用公式表示为：

         其中为节点u的第l层节点嵌入，N(u)是u的局部邻居，AGG是一个聚合函数（例如平均池化），是可训练的参数。输入的节点特征是一个长度为3的one-hot向量，用于表示LCG中的三种节点类型，即变量，变量的非和子句。G2SAT在此基础上，考虑到变量和它的非是密切相关的，因此在二者之间添加了额外的消息传递路径（在第一张图左侧图中用虚线表示）。

4.2 带有两阶段生成模式的可扩展的G2SAT

        LCG很多时候有成千上万的节点，因此在节点合并时，可选的节点对是非常多且不确定的，这使得归一化常数Z的计算是不可行的。为了避免这个问题，提出了两阶段的模式来实现节点的合并，即就是上文提到的节点提议阶段和节点合并阶段。节点提议阶段随机选取节点对，节点合并阶段模型只需要确定选取的节点对是否应该进行合并，从而将一个对数以万计的节点对选择问题转化为一个二元问题（nlp的掩码语言模型也存在过这个思路）。不直接从学习和采样，而是引用了中间变量u和v，代表两个待合并的节点，学习下面这个联合分布：

        其中，表示节点提议阶段，表示节点合并阶段。理论上， 可以是任何分布，只要它是非空的。LCG本身是一个静态图，对于如何一步步选择节点来指导这个迭代的节点合并过程几乎没有任何可用的经验和知识。因此节点提议阶段是随机选择节点对，在节点合并阶段，该模型只计算被选择的节点对的点积，而不是所有可能节点对的点积。然后，有如下公式：

        其中Uniform是一个离散的均匀分布。

 4.3 G2SAT的训练

        经过4.2的论述，模型的任务被确定为一个二元分类任务，即确定是否决定选择某一节点对执行合并。其交叉熵损失函数如下：

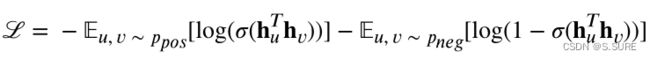
         和分别是训练中的正样本和负样本分布（二元分类问题的正负样本）。

        下面的算法从输入的二分图中获取必要的数据：

        输入一个二分图G，使用n次子句侧节点分割操作使得G被分解为一系列的树的集合。每一步中，随机选择子句节点中度大于1的节点执行分割操作，伪代码中为节点s分割后的两个新节点，作为数据集中的正样本，是从图中随机选择的不同于的节点，同时，节点对被视为数据集中的负样本。 (u+, v+, v−, Gi−1) 被保存在数据集中。同时，保存拆分步数n和拆分后的图G0用来初始化G2SAT模型。综上，该算法用于模型的数据集生成。

4.4 G2SAT的推理

        G2SAT的推理过程可以由下图所示的算法来描述。

        这个推理过程即就是获取数据集过程的逆过程，使用G0和步数n初始化G2SAT，G0是一系列树的集合，n是从二分图到G0所需要的拆分节点的次数。原则上讲G2SAT可以接受任意大小的二分图作为输入，并且迭代的次数是可变的，之所以用G0和n来控制是为了简化实验设计。在节点建议阶段，每次随机选取o个节点对并行提交给节点合并阶段。实践中发现，节点合并阶段学习正确预测一个正样本需要经过对大量的候选节点对进行抽样（因为抽样的节点对是完全公平地随机选取的，从概率论的角度来说，这就意味着只有当试验次数足够多时，频率才会更加逼近真实分布）。因此，在合并时，使用贪心算法从o个候选节点对中选取最可能被合并的节点对完成节点的合并，但这样的做法使生成器学习到的分布偏离了真实的数据分布，不过由此生成的图依然是合理的。在迭代n次后，生成的二分图Gn作为模型的输出。

5. Experiments

5.1 数据集和评估

        数据集：使用了来自SATLIB基准库和之前的SAT竞赛的10个小规模的现实SAT公式。这两个数据集的来源包含了从各种应用领域生成的SAT公式，例如有界模型检查等。使用SatElite预处理器删除公式中的重复子句，并进行了多项式时间的化简。经过预处理后的公式包含82~1122个变量，327~4455个子句。对于生成SAT公式的评估，使用图统计和SAT求解器性能来衡量其是否保留了输入的SAT公式的属性。然后作者调查了生成的SAT公式是否有助于帮助设计用于特定领域的SAT求解器。（注：由此推断，这个任务应该是对输入的SAT公式进行重构，从二分图的角度上通过子句的重写来生成等价的SAT公式）

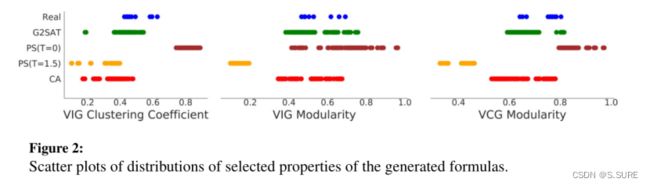
        图统计：即使用一些用于描述图相关性质的指标来评估生成的SAT公式。例如VIG、VCG和LCG中的模块性指标、VIG中的平均聚合系数以及VCG中的用变量和子句来计算的无标度结构参数等。

        SAT求解器性能：给定k个SAT求解器，对于原始SAT公式和G2SAT生成的公式，分别对这k个SAT求解器求解这些公式的性能进行排名，并比较两个排名的匹配程度。这里提出的是一种SAT求解器的相对性能的比较，分别在已有的SAT求解器中选择了表现最好的三个专用领域的SAT求解器I1，I2和I3，以及三个求解随机SAT实例的求解器R1，R2和R3，试验结果表明，在用于训练的公式上，I1、I2和I3的性能整体上要优于R1、R2和R3。因此对于生成的公式，根据求解的准确率，评估I系列的求解器的性能是否也优于R系列。

        应用（设计更好的SAT求解器）：作者用训练用的10个SAT公式以及G2SAT生成的10个SAT公式来引导当下一个使用广泛的SAT求解器Glucose的超参数选择。这里的超参数主要包括两个，即引导求解器决策变量顺序的参数，以及引导求解器执行子句删除的参数（有关于变量决策顺序的选择以及子句删除的相关知识可以学习CDCL算法进行了解）。的集合为{0.75,0.85,0.95}，的集合为{0.7,0.8,0.9,0.99,0.999}。文中使用网格搜索选择使得SAT求解器的性能最优的超参数。在评测时还使用了22个没有被其他模型发现过的真实SAT公式，因为更丰富的SAT公式有助于更好地指导SAT求解器的超参数选择。

5.2 模型

        将目前两个最SOTA的用于生成真实SAT公式的生成器作为baseline，使用G2SAT和baseline各生成200个SAT公式。之后是对三者的一些超参数设置的描述，用于尽可能地让三者在相似的设置下进行试验。

5.3 结果

        分别在5.1的三个标准下进行评估，即图统计、求解器性能、SAT求解器的优化。

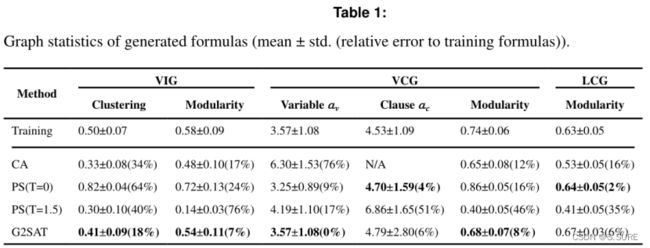
        图统计：从上表可以看出G2SAT比baseline在模块性和聚合性上有更好的拟合效果（而且CA被宣称定制用于拟合模块性特征）。括号里是生成的公式与原始公式之间的误差，综合来看，G2SAT生成的公式相对于基线方法，减小了更多的误差。

        上图中，每个点表示一个图（其实就是上表的统计图表示）。         

        SAT求解器性能：如上表，这里的排序规则前文已经讲过，可以发现只有CA和G2SAT生成的公式，很好的保留了SAT公式的信息，使得I系列的性能维持在R系列之前。 

        生成公式用于指导优化SAT求解器：从上表中可以看到，G2SAT生成的公式对超参数的引导使得SAT求解器获得了最大的运行时间加速。

5.4 结果分析

        G2SAT的可扩展性：G2SAT可用于更大规模的图的生成，相比于已有的生成图规模为1000节点的生成器，G2SAT可生成的最大图规模为39578和节点和102927条边（单GPU下运行时间为489秒）。如下图所示，可以发现对于子句数量的增加，G2SAT生成图的所需时间约呈线性增长。

        G2SAT的外推能力：用于验证G2SAT在不同于训练集数据输入的条件下生成图的能力组织的外推实验，训练集数据规模为377~4555个子句，而测试要生成的图的规模为13028~27360个子句。实验表明了对于更大规模的图生成问题，G2SAT生成的图也保留了原始SAT公示的重要属性，验证了其良好的外推能力。

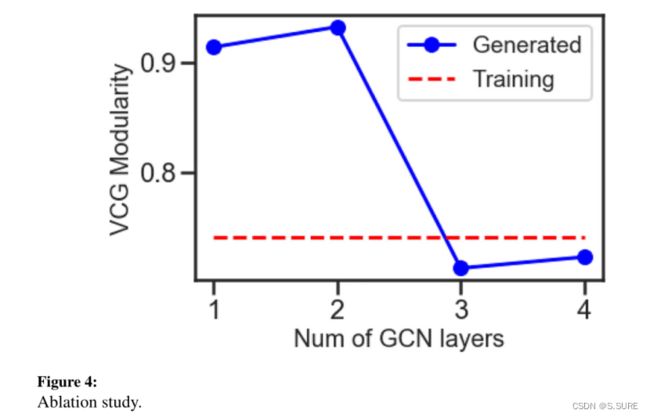
        消融实验：这里证明了GCN表达能力很大程度上会影响所生成的公式。如下图所示，随着GCN层数的增加（这意味更好的表达能力），生成公式的模块性这个属性的值越来越接近于原始公式（误差越来越小），同时对于聚合性这个属性也表现了相同的趋势（不过作者没有给图）。

6. 总结

        文章提出了第一个不依赖于手工算法的SAT公式的深度生成模型，根据输入的公式生成与之相似的SAT公式。future work是更大规模的SAT公式生成。

7. Appendix

        介绍了模型的训练硬件环境和评估方法，以及关于baseline方法的一些更细节的内容。