数据挖掘实验——python实现决策树（ID3算法）

实验内容：

使用ID3算法设计实现决策树，使用uci数据集中的Caesarian Section Classification Dataset Data Set数据进行分类

获取数据集：https://archive.ics.uci.edu/ml/datasets/Caesarian+Section+Classification+Dataset

数据集：
@attribute ‘Age’ { 22,26,28,27,32,36,33,23,20,29,25,37,24,18,30,40,31,19,21,35,17,38 }
@attribute ‘Delivery number’ { 1,2,3,4 }
@attribute ‘Delivery time’ { 0,1,2 }
@attribute ‘Blood of Pressure’ { 2,1,0 }

@attribute ‘Heart Problem’ { 1,0 }
@attribute Caesarian { 0,1 }

代码实现：

import pandas as pd

# 加载数据集
# @attribute 'Age' { 22,26,28,27,32,36,33,23,20,29,25,37,24,18,30,40,31,19,21,35,17,38 } 
# @attribute 'Delivery number' { 1,2,3,4 }
# @attribute 'Delivery time' { 0,1,2 }
# @attribute 'Blood of Pressure' { 2,1,0 }

# @attribute 'Heart Problem' { 1,0 } 
# @attribute Caesarian { 0,1 }
data= pd.read_csv('D:/Desktop/caesarian.csv.arff',header=None)
print(data.head())

import math
import operator

def get_data():
    # 数据集
    x = data[[0,1,2,3,4,5]].values.tolist()
    # 分类属性
    labels = ['年龄','数量','时间','血压','心脏病']
    return x,labels

def maxCount(classList):
    Count={}
    #统计classList中每个元素出现的次数
    for i in classList:
        if i not in classCount.keys():
            Count[i]=0
        Count[i]+=1
        #根据字典的值降序排列
        sorted_Count=sorted(Count.items(),key=operator.itemgetter(1),reverse=True)
        return sorted_Count[0][0]

def Entropy(x):
    D=len(x)
    #保存每个标签（label）出现次数的字典
    labelCounts={}
    #对每组特征向量进行统计
    for m in x:
        Label=m[-1]                     #提取标签
        if Label not in labelCounts.keys():   #标签没有被统计就添加
            labelCounts[Label]=0
        labelCounts[Label]+=1

    k=0.0
    #利用公式计算信息熵
    for key in labelCounts:
        P=float(labelCounts[key])/D
        k-=P*math.log(P,2)
    return k


def splitData(x, i, value):
    retData=[]
    for featVec in x:
        if featVec[i]==value:
            reducedFeatVec=featVec[:i]
            reducedFeatVec.extend(featVec[i+1:])
            retData.append(reducedFeatVec)
    return retData


# 选择最优特征
def best_label(x):
    # 特征数量
    numLabels = len(x[0]) - 1
    #信息熵oldEntropy
    oldEntropy = Entropy(x)
    #信息增益newsAdd
    newsAdd = 0.0
    #最优特征的索引值
    bestFeature = -1
    #遍历所有特征
    for i in range(numLabels):
        # 获取dataSet的第i个所有特征
        featList = [test[i] for test in x]
        #去重
        uniqueVals = set(featList)
        newEntropy = 0.0
        #计算信息增益
        for value in uniqueVals:
            #subData划分后的子集
            subData = splitData(x, i, value)
            p = len(subData) / float(len(x))
            newEntropy += p * Entropy((subData))
        #信息增益
        Add = oldEntropy - newEntropy
        print("第%d个特征增益为%.3f" % (i, Add))
        # 更新最大信息增益
        if (Add > newsAdd):
            newsAdd = Add
            bestFeature = i
    return bestFeature
    
def createTree(x,label,featLabels):
	labels=label.copy()
    # 取分类标签(0,1)
    classList=[test[-1] for test in x]
    # 如果类别完全相同，则停止继续划分
    if classList.count(classList[0])==len(classList):
        return classList[0]
    if len(x[0])==1:
        return maxCount(classList)
    bestFeat=best_label(x)
    bestFeatLabel=labels[bestFeat]
    labels.append(bestFeatLabel)
    #最优特征的标签生成树
    tree={bestFeatLabel:{}}
    #删除已使用的特征
    del(labels[bestFeat])

    #得到训练集中所有最优特征的属性值
    featValues=[test[bestFeat] for test in x]
    #去重
    uniqueVls=set(featValues)
    #遍历特征，创建决策树
    for value in uniqueVls:
        tree[bestFeatLabel][value]=createTree(splitData(x,bestFeat,value),labels,featLabels)
    return tree

if __name__=='__main__':
    data= pd.read_csv('D:/Desktop/caesarian.csv.arff',header=None)
    data[0][data[0] < 24] = 0
    data[0][(data[0] > 23) & (data[0] < 31)] = 1
    data[0][30 < data[0]] = 2
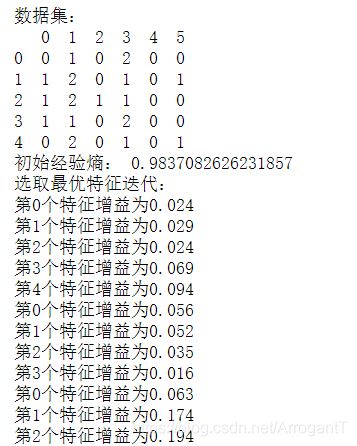
    print("数据集：")
    print(data.head())
    x,labels=get_data()
    print("初始经验熵：",Entropy(x))
    featLabels=[]
    print("选取最优特征迭代：")
    tree=createTree(x,labels,featLabels)
    print("决策树:")
    print(tree)
    
   

运行结果：

绘图代码：

from math import log
import operator
from matplotlib.font_manager import FontProperties
import matplotlib.pyplot as plt

# 函数说明：获取决策树叶子节点的数目

# Parameters：
#     myTree：决策树
# Returns：
#     numLeafs：决策树的叶子节点的数目
def getNumLeafs(myTree):
    numLeafs=0
    firstStr=next(iter(myTree))
    secondDict=myTree[firstStr]
    for key in secondDict.keys():
        if type(secondDict[key]).__name__=='dict':
            numLeafs+=getNumLeafs(secondDict[key])
        else: numLeafs+=1
    return numLeafs

# 函数说明:获取决策树的层数

# Parameters:
#     myTree:决策树
# Returns:
#     maxDepth:决策树的层数

def getTreeDepth(myTree):
    maxDepth = 0                                                #初始化决策树深度
    firstStr = next(iter(myTree))                                #python3中myTree.keys()返回的是dict_keys,不在是list,所以不能使用myTree.keys()[0]的方法获取结点属性，可以使用list(myTree.keys())[0]
    secondDict = myTree[firstStr]                                #获取下一个字典
    for key in secondDict.keys():
        if type(secondDict[key]).__name__=='dict':                #测试该结点是否为字典，如果不是字典，代表此结点为叶子结点
            thisDepth = 1 + getTreeDepth(secondDict[key])
        else:   thisDepth = 1
        if thisDepth > maxDepth: maxDepth = thisDepth            #更新层数
    return maxDepth

# 函数说明:绘制结点

# Parameters:
#     nodeTxt - 结点名
#     centerPt - 文本位置
#     parentPt - 标注的箭头位置
#     nodeType - 结点格式
# Returns:
#     无
def plotNode(nodeTxt, centerPt, parentPt, nodeType):
    arrow_args = dict(arrowstyle="<-")                                            #定义箭头格式
    font = FontProperties(fname=r"c:\windows\fonts\simsun.ttc", size=14)        #设置中文字体
    createPlot.ax1.annotate(nodeTxt, xy=parentPt,  xycoords='axes fraction',    #绘制结点
        xytext=centerPt, textcoords='axes fraction',
        va="center", ha="center", bbox=nodeType, arrowprops=arrow_args, FontProperties=font)
    
# 函数说明:标注有向边属性值

# Parameters:
#     cntrPt、parentPt - 用于计算标注位置
#     txtString - 标注的内容
# Returns:
#     无
def plotMidText(cntrPt, parentPt, txtString):
    xMid = (parentPt[0]-cntrPt[0])/2.0 + cntrPt[0]                                            #计算标注位置
    yMid = (parentPt[1]-cntrPt[1])/2.0 + cntrPt[1]
    createPlot.ax1.text(xMid, yMid, txtString, va="center", ha="center", rotation=30)
    
# 函数说明:绘制决策树

# Parameters:
#     myTree - 决策树(字典)
#     parentPt - 标注的内容
#     nodeTxt - 结点名
# Returns:
#     无
def plotTree(myTree, parentPt, nodeTxt):
    decisionNode = dict(boxstyle="sawtooth", fc="0.8")                                        #设置结点格式
    leafNode = dict(boxstyle="round4", fc="0.8")                                            #设置叶结点格式
    numLeafs = getNumLeafs(myTree)                                                          #获取决策树叶结点数目，决定了树的宽度
    depth = getTreeDepth(myTree)                                                            #获取决策树层数
    firstStr = next(iter(myTree))                                                            #下个字典
    cntrPt = (plotTree.xOff + (1.0 + float(numLeafs))/2.0/plotTree.totalW, plotTree.yOff)    #中心位置
    plotMidText(cntrPt, parentPt, nodeTxt)                                                    #标注有向边属性值
    plotNode(firstStr, cntrPt, parentPt, decisionNode)                                        #绘制结点
    secondDict = myTree[firstStr]                                                            #下一个字典，也就是继续绘制子结点
    plotTree.yOff = plotTree.yOff - 1.0/plotTree.totalD                                        #y偏移
    for key in secondDict.keys():
        if type(secondDict[key]).__name__=='dict':                                            #测试该结点是否为字典，如果不是字典，代表此结点为叶子结点
            plotTree(secondDict[key],cntrPt,str(key))                                        #不是叶结点，递归调用继续绘制
        else:                                                                                #如果是叶结点，绘制叶结点，并标注有向边属性值
            plotTree.xOff = plotTree.xOff + 1.0/plotTree.totalW
            plotNode(secondDict[key], (plotTree.xOff, plotTree.yOff), cntrPt, leafNode)
            plotMidText((plotTree.xOff, plotTree.yOff), cntrPt, str(key))
    plotTree.yOff = plotTree.yOff + 1.0/plotTree.totalD
    
# 函数说明:创建绘制面板

# Parameters:
#     inTree - 决策树(字典)
# Returns:
#     无
def createPlot(inTree):
    fig = plt.figure(1, facecolor='white')#创建fig
    fig.clf()#清空fig
    axprops = dict(xticks=[], yticks=[])
    createPlot.ax1 = plt.subplot(111, frameon=False, **axprops)#去掉x、y轴
    plotTree.totalW = float(getNumLeafs(inTree))#获取决策树叶结点数目
    plotTree.totalD = float(getTreeDepth(inTree))#获取决策树层数
    plotTree.xOff = -0.5/plotTree.totalW; plotTree.yOff = 1.0#x偏移
    plotTree(inTree, (0.5,1.0), '')#绘制决策树
    plt.show()#显示绘制结果

if __name__ == '__main__':
    dataSet, labels = get_data()
    featLabels = []
    myTree = createTree(dataSet, labels, featLabels)
    print(myTree)
    createPlot(myTree)