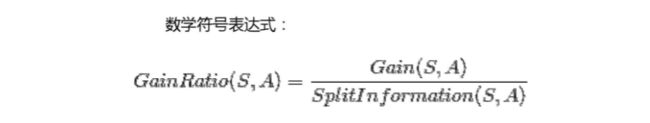ID3、C4.5决策树算法的Python实现(注释详细)
一、决策树之ID3和C4.5简介
决策树(Decision Tree),每个分支都是需要通过条件判断进行划分的树,解决分类和回归问题的方法。决策树是最经常使用的数据挖掘算法,其核心是一个贪心算法,它采用自顶向下的递归方法构建决策树。
目前常用的决策树算法有ID3算法、改进的C4.5,C5.0算法和CART算法
ID3算法的核心是在决策树各级节点上选择属性时,用信息增益作为属性的选择标准,使得在每一个非节点进行测试时,能获得关于被测试记录最大的类别信息。C4.5在选取最优特征时,采用的衡量标准是信息增益率。
ID3的特点
优点:理论清晰,方法简单,学习能力较强
缺点:
(1) 信息增益的计算比较依赖于特征数目比较多的特征
(2) ID3为非递增算法
(3) ID3为单变量决策树
(4) 抗糙性差
C4.5的改进之处:
(1) 通过信息增益率选择属性
(2) 处理连续型数据的属性
(3) 能够进行剪枝操作
(4) 能够对空缺值进行处理
二、信息熵、信息增益、分离信息、信息增益率
设S是训练样本集,它包括n个类别的样本,这些方法用Ci表示,那么熵和信息增益用下面公式表示:
1. 信息熵:

其中pi表示Ci的概率
2. 样本熵:
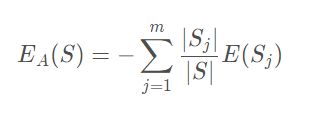
其中Si表示根据属性A划分的S的第i个子集,S和Si表示样本数目
3. 信息增益:
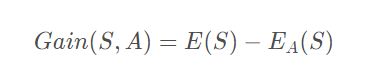
ID3中样本分布越均匀,它的信息熵就越大,所以其原则就是样本熵越小越好,也就是信息增益越大越好。
4. 分离信息
5. 信息增益率
三、ID3决策树构造算法的Python实现
from math import log
# 构造数据集
def create_dataset():
dataset = [['youth', 'no', 'no', 'just so-so', 'no'],
['youth', 'no', 'no', 'good', 'no'],
['youth', 'yes', 'no', 'good', 'yes'],
['youth', 'yes', 'yes', 'just so-so', 'yes'],
['youth', 'no', 'no', 'just so-so', 'no'],
['midlife', 'no', 'no', 'just so-so', 'no'],
['midlife', 'no', 'no', 'good', 'no'],
['midlife', 'yes', 'yes', 'good', 'yes'],
['midlife', 'no', 'yes', 'great', 'yes'],
['midlife', 'no', 'yes', 'great', 'yes'],
['geriatric', 'no', 'yes', 'great', 'yes'],
['geriatric', 'no', 'yes', 'good', 'yes'],
['geriatric', 'yes', 'no', 'good', 'yes'],
['geriatric', 'yes', 'no', 'great', 'yes'],
['geriatric', 'no', 'no', 'just so-so', 'no']]
features = ['age', 'work', 'house', 'credit']
return dataset, features
# 计算信息熵
def compute_entropy(dataset):
# 求总样本数
num_of_examples = len(dataset)
labelCnt = {}
# 遍历整个样本集合
for example in dataset:
# 当前样本的标签值是该列表的最后一个元素
currentLabel = example[-1]
# 统计每个标签各出现了几次
if currentLabel not in labelCnt.keys():
labelCnt[currentLabel] = 0
labelCnt[currentLabel] += 1
entropy = 0.0
# 对于原样本集,labelCounts = {'no': 6, 'yes': 9}
# 对应的初始shannonEnt = (-6/15 * log(6/15)) + (- 9/15 * log(9/15))
for key in labelCnt:
p = labelCnt[key] / num_of_examples
entropy -= p * log(p, 2)
return entropy
# 提取子集合
# 功能:从dataSet中先找到所有第axis个标签值 = value的样本
# 然后将这些样本删去第axis个标签值,再全部提取出来成为一个新的样本集
def create_sub_dataset(dataset, index, value):
sub_dataset = []
for example in dataset:
current_list = []
if example[index] == value:
current_list = example[:index]
current_list.extend(example[index + 1 :])
sub_dataset.append(current_list)
return sub_dataset
def choose_best_feature(dataset):
num_of_features = len(dataset[0]) - 1
# 计算当前数据集的信息熵
current_entropy = compute_entropy(dataset)
# 初始化信息增益率
best_information_gain_ratio = 0.0
# 初始化最佳特征的下标为-1
index_of_best_feature = -1
# 通过下标遍历整个特征列表
for i in range(num_of_features):
# 构造所有样本在当前特征的取值的列表
values_of_current_feature = [example[i] for example in dataset]
unique_values = set(values_of_current_feature)
# 初始化新的信息熵
new_entropy = 0.0
# 初始化分离信息
split_info = 0.0
for value in unique_values:
sub_dataset = create_sub_dataset(dataset, i, value)
p = len(sub_dataset) / len(dataset)
# 计算使用该特征进行样本划分后的新信息熵
new_entropy += p * compute_entropy(sub_dataset)
# 计算分离信息
split_info -= p * log(p, 2)
# 计算信息增益
# information_gain = current_entropy - new_entropy
# 计算信息增益率(Gain_Ratio = Gain / Split_Info)
information_gain_ratio = (current_entropy - new_entropy) / split_info
# 求出最大的信息增益及对应的特征下标
if information_gain_ratio > best_information_gain_ratio:
best_information_gain_ratio = information_gain_ratio
index_of_best_feature = i
# 这里返回的是特征的下标
return index_of_best_feature
# 返回具有最多样本数的那个标签的值('yes' or 'no')
def find_label(classList):
# 初始化统计各标签次数的字典
# 键为各标签,对应的值为标签出现的次数
labelCnt = {}
for key in classList:
if key not in labelCnt.keys():
labelCnt[key] = 0
labelCnt[key] += 1
# 将classCount按值降序排列
# 例如:sorted_labelCnt = {'yes': 9, 'no': 6}
sorted_labelCnt = sorted(labelCnt.items(), key = lambda a:a[1], reverse = True)
# 下面这种写法有问题
# sortedClassCount = sorted(labelCnt.iteritems(), key=operator.itemgetter(1), reverse=True)
# 取sorted_labelCnt中第一个元素中的第一个值,即为所求
return sorted_labelCnt[0][0]
def create_decision_tree(dataset, features):
# 求出训练集所有样本的标签
# 对于初始数据集,其label_list = ['no', 'no', 'yes', 'yes', 'no', 'no', 'no', 'yes', 'yes', 'yes', 'yes', 'yes', 'yes', 'yes', 'no']
label_list = [example[-1] for example in dataset]
# 先写两个递归结束的情况:
# 若当前集合的所有样本标签相等(即样本已被分“纯”)
# 则直接返回该标签值作为一个叶子节点
if label_list.count(label_list[0]) == len(label_list):
return label_list[0]
# 若训练集的所有特征都被使用完毕,当前无可用特征,但样本仍未被分“纯”
# 则返回所含样本最多的标签作为结果
if len(dataset[0]) == 1:
return find_label(label_list)
# 下面是正式建树的过程
# 选取进行分支的最佳特征的下标
index_of_best_feature = choose_best_feature(dataset)
# 得到最佳特征
best_feature = features[index_of_best_feature]
# 初始化决策树
decision_tree = {best_feature: {}}
# 使用过当前最佳特征后将其删去
del(features[index_of_best_feature])
# 取出各样本在当前最佳特征上的取值列表
values_of_best_feature = [example[index_of_best_feature] for example in dataset]
# 用set()构造当前最佳特征取值的不重复集合
unique_values = set(values_of_best_feature)
# 对于uniqueVals中的每一个取值
for value in unique_values:
# 子特征 = 当前特征(因为刚才已经删去了用过的特征)
sub_features = features[:]
# 递归调用create_decision_tree去生成新节点
decision_tree[best_feature][value] = create_decision_tree(create_sub_dataset(dataset, index_of_best_feature, value), sub_features)
return decision_tree
# 用上面训练好的决策树对新样本分类
def classify(decision_tree, features, test_example):
# 根节点代表的属性
first_feature = list(decision_tree.keys())[0]
# second_dict是第一个分类属性的值(也是字典)
second_dict = decision_tree[first_feature]
# 树根代表的属性,所在属性标签中的位置,即第几个属性
index_of_first_feature = features.index(first_feature)
# 对于second_dict中的每一个key
for key in second_dict.keys():
if test_example[index_of_first_feature] == key:
# 若当前second_dict的key的value是一个字典
if type(second_dict[key]).__name__ == 'dict':
# 则需要递归查询
classLabel = classify(second_dict[key], features, test_example)
# 若当前second_dict的key的value是一个单独的值
else:
# 则就是要找的标签值
classLabel = second_dict[key]
return classLabel
if __name__ == '__main__':
dataset, features = create_dataset()
decision_tree = create_decision_tree(dataset, features)
# 打印生成的决策树
print(decision_tree)
# 对新样本进行分类测试
features = ['age', 'work', 'house', 'credit']
test_example = ['midlife', 'yes', 'no', 'great']
print('\n',classify(decision_tree, features, test_example))
四、C4.5决策树构造算法的Python实现
只要改动一下函数choose_best_feature,将里面的计算信息增益变为计算信息增益率即可。