深度学习修炼（三）——自动求导机制

致谢

Pytorch中常用的四种优化器SGD、Momentum、RMSProp、Adam - 简书 (jianshu.com)

反向传播算法（过程及公式推导）_好的嗡嗡嗡的博客-CSDN博客

动手学深度学习——矩阵求导之自动求导_时生丶的博客-CSDN博客

(1条消息) Pytorch入门（四）——计算图与自动求导_xinye0090的博客-CSDN博客

(1条消息) pytorch 计算图以及backward_coderwangson的博客-CSDN博客_pytorch清空计算图

3 自动求导机制

要明白自动求导机制，我们就要先知道计算图是什么。在后面的学习中，我们会学习到多层感知机，而为了计算多层感知机，我们求需要动用计算图和利用自动求导。

3.1 传播机制与计算图

pytorch框架和TensorFlow框架在计算图中最大的不同是：pytorch是动态的计算图，它能边搭建边运行；而TensorFlow是静态的计算图，它必须先把图搭建好后才能开始计算。

3.1.1 前向传播

我们来看看什么是前向传播。前向传播英文是(forward propagation或forward pass)，它指的是：按顺序（从输入层到输出层）计算和存储神经网络中每层的结果。

如果你听不懂的话，可以看一下下面前向传播的计算图。

上述的计算图反映了一件事，如果把上述过程看做是神经网络，那么前向传播实际上是在计算每一层的值。

3.1.2 反向传播

比较重要的是反向传播。反向传播（backward propagation或backpropagation)指的是计算神经网络参数梯度的方法。简而言之就是，该方法根据微积分中的链式规则，按相反的顺序从输出层到输入层遍历网络。同理，反向传播计算图如下图所示。

反向传播实际上就是根据求导，来算出某一节点对于另外的某一节点所给的“回馈”。即导数，但是对于多个变量求偏导，我们叫其结果为梯度。

3.2 自动求导

pytorch为我们提供了自动求导机制，其机制用torch.autograd来实现。为了照顾新手，我们不直接给出API，而采取循循引诱的方式来讲解。

对于pytorch的自动求导来说，由于版本的更新迭代，老版本的实现和新版本的实现大有差异，在老版本中，自动求导必须调用autograd.Variable来把变量包装起来，而新版本则不需要了，只需在需要自动求导的张量里添加requires_grad = True即可。

# 方法1
x = torch.randn(3,4,requires_grad = True)
x

out：

tensor([[-0.1225, 0.5622, 0.3288, -1.2560],
[-0.7067, 0.2453, 1.8471, 0.9765],
[-0.7606, 0.8300, -0.9079, -0.2566]], requires_grad=True)

上述的方法是下面方法的简化版。

# 方法2
x = torch.randn(3,4)
x.requires_grad = True
x

out：

tensor([[-0.3050, 1.6089, 0.4765, 0.8169],
[-1.4941, -0.9640, 0.4670, -1.5811],
[ 0.1837, -0.5159, 0.4066, 1.8279]], requires_grad=True)

以上的两个方法均可以使用。

我们单单只是构建张量可不够，只要一个张量要求啥子导。我们在构建一个张量b。

b = torch.randn(3,4,requires_grad = True)

做完上述的步骤后，我们构建一个没有权重的线性模型。

# 构建一个线性模型
t = x + b

当我们做完上述的步骤后，实际上一个比较简单的神经网络就搭建起来了。

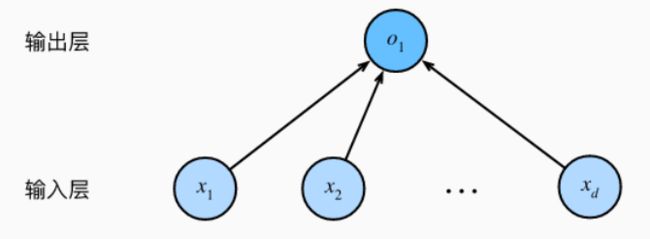
如果我们把线性回归描述成神经网络。那么我们的输入层就是所有的特征，而输出层就是预测值。

在如图所示的神经网络中，输入为$x_1,x_2...x_d$，因此输入层中的输入数（由于我们常常把输入的特征放入向量，实际上向量的长度就是维度，故我们把输入数也叫特征维度）为d。

由于我们通常计算时发生在输出层里，输入层只是负责传入数据，所以一般输入层不算入层数，这么说下来，我们可以得出结论：这是一个单层神经网络。

再啰嗦几句，上面的输入层把数据输到输出层，所以给人感觉就好像输出层一下子要处理很多的输入（笑。。。不知道你能不能get到那种感觉），所以这大概率为什么这种输入到输出的变化被叫做全连接层(fully_connected layer)或称为稠密层(dense layer)的原因了。

好，回到我们的主题，既然已经搭好了一个线性回归模型了，我们怎么使其反向传播？我们知道，反向传播的前提条件是要知道前向传播中的输出值。所以我们继续往下：

y = t.sum
y

out：

tensor(-1.6405, grad_fn=)

在pytorch中，如果需要反向传播，只需在每个张量里指定自动求导，而后在最后一步调用以上方法即可。如在本例中，调用y.backward即可进行反向传播。

y.backward() 

而后，如果我们想看b的梯度，我们可以通过以下的方式：

b.grad

out：

tensor([[1., 1., 1., 1.],
[1., 1., 1., 1.],
[1., 1., 1., 1.]])

这里可能会有一个疑问哈，y已经进行反向传播了，此时如果通过变量.grad调用的是什么梯度？因为你使用的是y的反向传播，拿b来举例，b.grad实际上就是求y对于b的偏导。

还有一个问题是，在上述的操作过程中，我们并没有打开t张量的自动求导开关，那他是否也能自动求导得到梯度呢？

我们调用tensor.requires_grad即可查看该张量是否打开了自动求导开关。

x.requires_grad,b.requires_grad,t.requires_grad

out：

(True, True, True)

以上的结果侧面印证了一个问题，即使没有指定某一张量可自动求导，但是和打开自动求导的张量进行运算时，其运算结果的自动求导开关也会被打开。

3.3 再来做一次

我相信经过上面的一次操作，你已经大概知道torch的自动求导机制了。我们趁热打铁，试着做一下下面的工作。

如果我们要对上述的计算图计算的话，我们可以进行以下步骤：

# 计算流程
x = torch.rand(1)
b = torch.rand(1,requires_grad = True)
w = torch.rand(1,requires_grad = True)
y = w * x
z = y + b

# 我们查看各参数的自动求导打开情况
x.requires_grad, b.requires_grad, w.requires_grad, y.requires_grad

out：

(False, True, True, True)

实际上，我们还可以把计算图看成计算树来查看哪些参数是叶子结点。

# 我们还可以看一下哪些参数为计算图（树）的叶子结点
x.is_leaf, b.is_leaf, w.is_leaf, y.is_leaf, z.is_leaf

out：

(True, True, True, False, False)

当上述处理完毕后，我们对z进行反向传播计算。

z.backward(retain_graph = True) # 保存计算图

然后我们分别查看下面参数的梯度。

w.grad

out：

tensor([0.3843])

b.grad

out：

tensor([1.])

你可以在jupyter notebook上执行完上述的两个参数的梯度后再执行一次，第二次时，你发现它们居然是第一次运行结果的两倍了。也是因为我们在z的反向传播时指定保存计算计算图，使得后面在计算某参数的梯度时，他都是根据上一次计算图的结果继续累加。

3.4 线性回归

继机器学习一别，我们已经许久未见狭义线性模型了。对此，我们希望在深度学习中能再次实现它。

3.4.1 回归

回归，英文名regression。在先修课机器学习中，我们经常能够遇见两个名词：回归和分类。这两者的区别实际上就是：回归是根据以往的经验来预测未来的趋势或走向，比如说经典的房价预测问题；而分类是根据根据以往的经验来预测下一个东西是属于什么，经典的就是二分类问题；从宏观上来看，回归是相对于连续的，而分类是相对于离散的。

3.4.2 线性回归的基本元素

线性回归基于几个简单的假设：首先，假设自变量x和因变量y之间的关系是线性的，即y可以表示为x中元素的加权和，这里通常允许包含观测值的一些噪声；其次，我们假设任何噪声都比较正常，如噪声遵循正态分布。

为了解释线性回归，我们举一个实际的例子，我们希望根据房屋的面积和房龄来估算房屋的价格。接下来这里涉及到许多机器学习的术语；为了开发一个能够预测房价的模型，我们需要收集一个真实的数据集，这个数据集包括了以往房屋的预售价格、面积和房龄，当然，如果你要收集更多的特征也不是不行，但是我们目前从最简单的开始讲起。

在机器学习的术语中，我们把这部分收集来用作训练房价模型的数据集叫做训练数据集(training data set)或训练集(training set)。每行数据或者用数据库的术语来说叫元组在这里称为样本，也可以称为数据样本(training instance)或者数据点(data point)。我们把试图预测的目标(在这个例子中指的是房屋价格)称为标签(label)或者目标(target)。预测所依据的自变量(在这个例子中指的是面积和房龄)称为特征(feature)或者协变量(covariate)。

通常，我们使用n来表示数据集中的样本数。对索引为i的样本，其输入表示为：$x^{(i)}=[x_1^{(i)},x_2^{(i)}{]}^T$，其对应的标签是$y^{(i)}$。

3.4.3 线性模型

线性假设是指目标可以表示为特征的加权和，也就是我们高中所熟悉的一次函数y = kx+b，只是在深度学习中，我们换成了$y=w_1{x}_1+w_2{x}_2+....+b$。其中$w$叫做权重(weight)，b叫做截距(intercept)，b在高中数学中叫截距比较多一点，但是在深度学习中它通常被叫做偏置(bias)。偏置是指当前所有特征都取值为0时，预测值应该为多少。虽然特征取值为0可能在我们说的预测房价的例子中并不存在，但是我们仍然需要偏置，因为如果没有偏置那我们的模型会受到限制。

严格来说，如果应用到房价预测的例子上的话，我们可以写出这样的式子：$price=w_{area}\cdot area+w_{age}\cdot age+b$

如果是单纯地一个特征就写一个x，那个式子就会变为：$y=w_1{x}_1+w_2{x}_2+....w_n{x}_n+b$，这样的话实际上不利于我们计算，而且不简洁。根据我们线性代数学过的知识，我们知道可以用向量存放特征，即x = {x1,x2,x3…xn}，当然，这仅仅是一个样本，如果是多样本的话，我们可以用矩阵来放。X的每一行是一个样本，每一列是一种特征
KaTeX parse error: Undefined control sequence: \ at position 115: … \end{bmatrix} \̲ ̲
如同我们前面所说，下标表示第几个特征，上标表示第几个样本。

同样地我们也把权重w放进矩阵，那么模型简化为：$\hat{y}=w^{T}x+b$

其中w之所以加转置是因为矩阵乘法就是$A^{T}B$。而w和x两个矩阵相乘后，由于b是标量，这个时候就会用到python的广播机制去相加。

在我们给定训练数据X和对应的已知标签y后，线性回归的目标就是找到一组权重向量w和偏置b，找到后这个模型就确定下来了；当有新的x进来后，这个模型预测的y能够和真实的y尽可能的接近。

虽然我们相信给定x预测y的最佳模型会是线性的，但我们很难找到一个有n个样本的真实数据集，然后算出来的结果真的是线性的，这根线一点弯曲都没有，这是不可能的。因此，即使我们确信他们的潜在关系是线性，我们也需要加入一个噪声项来考虑误差所带来的影响。

3.4.4 线性回归的实现

3.4.4.1 获取数据集

上面一直在吹理论，实际上，如果你看过我的机器学习中关于线性回归的阐述，应该是或多或少了解的。而本小节的重点，我们将会放在如何用torch提供的API去实现一个线性回归上。

继上一小节最后说的，我们很难找到一个数据集用于构建线性模型，为此，我们自己捏一个出来。

import numpy as np
import matplotlib.pyplot as plt

x_values = [i for i in range(11)]
x_train = np.array(x_values,dtype=np.float32)
x_train = x_train.reshape(-1,1)
x_train

y_values = [2*i +1 for i in x_values]
y_train = np.array(y_values,dtype=np.float32)
y_train = y_train.reshape(-1,1)
y_train

捏造出数据集后，我们可视化这些数据集看一下长啥样。

plt.figure()
plt.scatter(x_train,y_train)
plt.show()

out：

3.4.4.2 模型搭建

当我们获取到数据集后，我们要做的第二步是搭建一个线性模型。

#导入模块
import torch.nn as nn
import torch

class LinearRegressionModel(nn.Module):
    def __init__(self,input_dim,output_dim):
        super(LinearRegressionModel,self).__init__()
        self.linear = nn.Linear(input_dim,output_dim) #全连接层
    # 前向传播    
    def forward(self,x):
        out = self.linear(x)
        return out

在上述的类中，我们需要去继承torch.nn.Module包，以方便我们后续神经网络层搭建。继承完毕后，我们设定类中初始化方法，我们调用父类方法初始化，并且指定我们要搭建的线性回归神经网络的层，在这里，我们需要的仅仅是一个有输入和输出的全连接层，且其中不需要添加激活函数，我们调用nn.Linear(input_dim,output_dim)即可搭建，里面传入的参数分别是输入数据的维度和输出数据的维度，在线性回归中，通过输入数据和输出数据的维度全设为1即可。

除了初始化，我们还需要在类中添加一个前向传播成员函数，前向传播的计算实际上就是上面nn.Linear()输入数据后得出的结果。

搭建好神经网络后，我们需要实例化神经网络类并且为其传参。

# 实例化类
model = LinearRegressionModel(input_dim=1,output_dim=1)
model

out：

LinearRegressionModel(
(linear): Linear(in_features=1, out_features=1, bias=True)
)

3.4.4.3 损失函数

搭建好模型后，我们还需要搭建损失函数，以此训练模型。

epochs = 1000 #训练次数
learning_rate = 0.01 #学习率
# 优化器
optimizer = torch.optim.SGD(model.parameters(),lr = learning_rate)
# 优化器使用的误差函数
criterion = nn.MSELoss()

在上面的代码中，我们调用torch.optim包下的SGD(随机梯度下降法)来优化我们的训练模型，并且我们采用均方误差（Mean Square Error,MSE）进行梯度下降。SGD的有参构造器中需要传入我们神经网络对象中所有参数，并且还要传入一个学习率。

定义好损失函数后，下一步，我们就该进行训练了。

3.4.4.4 训练模型

我们着重训练我们的模型。

for epoch in range(epochs):
    # 每梯度下降一次，epoch+1
    epoch += 1
    # 前面的数据是array格式，torch只能处理tensor格式
    inputs = torch.from_numpy(x_train)
    labels = torch.from_numpy(y_train)
    
    # 梯度要清零每一次迭代
    optimizer.zero_grad()
    
    # 前向传播
    outputs = model(inputs)
    
    # 计算损失
    loss = criterion(outputs,labels)
    
    # 反向传播
    loss.backward()
    
    # 更新权重参数
    optimizer.step()
    
    # 打印每五十次梯度下降后对应损失值
    if epoch % 50 == 0:
        print(f'epoch {epoch}, loss {loss.item()}')

out：

epoch 50, loss 0.23870129883289337
epoch 100, loss 0.13614629209041595
epoch 150, loss 0.07765268534421921
epoch 200, loss 0.04429023712873459
epoch 250, loss 0.02526141330599785
epoch 300, loss 0.014408227056264877
epoch 350, loss 0.008217886090278625
epoch 400, loss 0.00468717934563756
epoch 450, loss 0.0026733996346592903
epoch 500, loss 0.0015248022973537445
epoch 550, loss 0.0008696810691617429
epoch 600, loss 0.0004960428341291845
epoch 650, loss 0.00028292808565311134
epoch 700, loss 0.0001613689964869991
epoch 750, loss 9.204218804370612e-05
epoch 800, loss 5.2495626732707024e-05
epoch 850, loss 2.9940983949927613e-05
epoch 900, loss 1.7078866221709177e-05
epoch 950, loss 9.74200611381093e-06
epoch 1000, loss 5.556627456826391e-06

在第一讲中我们不是说了tensor很重要吗，现在可以告诉你为什么重要了，因为神经网络只接收tensor格式。所以对于array的数据，我们必须将其先转换为tensor再进行处理。

我们还要先注意在前面我们说过计算图可以保存梯度，为了防止误操作，我们在每次梯度下降时，我们都要清零迭代后的梯度数据。

接着我们需要计算前向传播，而后根据前向传播的输出值，通过损失函数反向传播，反向传播后优化器内参数不会自动更新需要手动更新。

训练完模型后，我们可以看看模型的预测结果，这里你照做就行，后面我再和你解释这是怎么一回事。

predicted = model(torch.from_numpy(x_train).requires_grad_()).data.numpy()
predicted

训练好的模型如果效果十分好，那我们可以选择保存该模型，以便下次的使用。保存模型的方法如下：

torch.save(model.state_dict(),'model.pkl')

需要知道的是，模型的保存是以字典形式进行保存，保存的仅仅是模型的参数，并且保存的名字为’model.pkl’且。

如果我们需要读入模型，可以如下：

# 读取模型
model.load_state_dict(torch.load('model.pkl'))

最后，在整个训练过程中，实际上我们并没有用到GPU来加速我们的训练过程，这是因为我们的模型十分简单，所有的数据集也很少。在面对大数据的时候，我们通常需要GPU来加速我们模型的训练，其方法是在实例化神经网络类后，将该对象传出cuda设备。并且在后面将训练集传入模型的时候，也要传入cuda。

#将神经网络对象传给设备
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
model.to(device)

#将数据传入cuda
inputs = torch.from_numpy(x_train).to(device)
Labels = torch.from_numpy(y_train).to(device)

3.5 后记

这一讲中讲的自动求导机制并没有什么复杂，并不需要魔化它，你需要知道的仅仅是：在构建数据集张量的时候打开自动求导，并且先计算前向传播后根据前向传播的值，输入损失函数然后反向传播更新参数即可。其他的底层的东西如果你真想弄明白，何必呢，你搞底层就不会来看我这一篇笔记了不是。而且人家框架就是为了让你避免重复造轮子。

至于3.4中线性回归模型的搭建，这只是一个简单到不能再简单的torch的初体验，实际上，里面的很多方法包含有很多的参数，都是我们不宜直接一波灌输进去的，在后面的学习中，我们会逐步地去掌握它们。