深度学习日记（一）

好了，我就是这么一个三心二意的人，这几天又鸽了leetcode和61B开始搞这个东西，
因为申请暑假实习的地方需要又DL框架基础，我就emmmm…

查了一下找到了比较基础的教程，最后在b站上找到了这个
【深度学习框架TensorFlow】零基础入门|应用
看了前几集讲解还比较清楚，主要用jupyter去编程。前两周都是环境的配置。
相关的import tensorflow找不到module 的问题在我另一篇blog里面有解决。

从第三周开始，涉及到一些神经网络的东西，他就默认你有一些深度学习基础了…建议没有基础的去看黄校长的教程，实在不知道这个黄校长是谁…就去找了其他的教程

最后在TesterHome上面找到一位叫孙高飞的用户分享的内容
链接如下深度学习基础—孙高飞

---

深度学习基础（一）二分类 by 孙高飞

链接在此： 深度学习基础–二分类

笔记整理：

人工智能 = 大数据+机器学习。

现阶段的人工智能是使用机器学习算法在大量的历史数据下进行训练
从历史数据中找到一定的规律并对未来做出的预测行为。

机器学习训练出来的模型可以暂且理解为一个二分类的模型。
主要是就是一个key，value的数据库。
key就是在数据中抽取出来的特征，value就是这个特征的权重。
想要预测一个用户的行为的时候，就从用户的数据中提取特征并在模型中查找对应的权重。
最后根据这些特征的权重算出一个分，即一个概率。

二分类

在⼆分类问题中，通常 分类的结果只有两个: 是(Yes)和不是(No)
比如判断图片中是否存在某物，那么我们为模型输入一张图片，得出一个预测值y。
y的取值为1或者0。0 代表是，1代表否。

逻辑回归 线性回归

逻辑回归是二分类算法中最典型的一个。 再说逻辑回归之前我们先说说线性回归。
如预测房价的例子，（设影响房价的因素只有面积） 如图为房价随着面积的变化趋势：

希望有一个函数y= wx +b，[x为面积，y为预测值]，输入房价后能得到一个预测的房价数值。
而机器学习要训练并学习的就是参数w和b。
根据 梯度下降的原理， 迭代训练中会不停的改变w和b的指，将得到 y 值于训练数据中实际的值(实际的房价)进行对比。 最后找到最优解(于实际值差距最小的w和b)。

再看y=wx + b这个函数，例子里只有面积这一特征，所以x是一个一维的特征向量(特征矩阵)。实际问题中影响房价的可能有多个因素，如地点，朝向等，则 x 为多维的特征向量。
函数为 y = w1*x1 + w2*x2 +w3*x3 ......... wn*xn + b。
暂且将模型理解为是一个是key-value [特征-权重] 的数据库，则公式中的w和b就相当于权重。

我们将每个特征和权重进行计算并累加，最后就是我们的预测值。

函数是线性函数，故称线性回归。 如下：

回归与分类

回归算法是 预测一个具体的值，就像上面我们说的预测房价 y=wx+b。
分类算法是在 一群实体中将物品进行分类，例如二分类算法中，预测值只有0和1。
逻辑回归算法是一个二分类算法，采用线性回归公式，即 y=wx+b。 期望值是0或者1。
所以我们需要一个额外的 激活函数 来把我们的预测值变换成0和1。
【这就是为什么逻辑回归虽然叫回归但却是二分类算法的原因(多了一个激活函数把预测值变换成0或者1的数值)。

激活函数

在神经网络中，激活函数能给神经网络加入一些非线性因素，使得神经网络可以更好地解决较为复杂的问题。例如我们给逻辑回归用的Sigmoid函数：

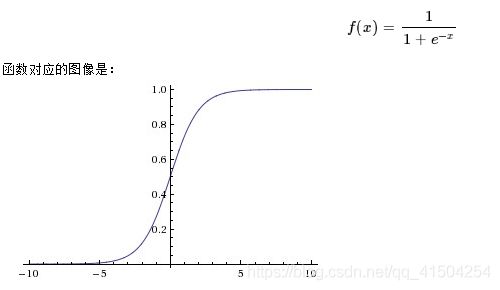
其他激活函数还有tanh， ReLU等。

逻辑回归与损失函数

逻辑回归是一个线性回归加上一个sigmoid函数，如下：

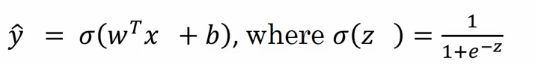
根据梯度下降的原理，算法不停改变 w 和 b 的值，以找到合适的 w 和 b 的值让预测的 y 值跟实际的 y 值差距最小。则需要一个损失函数来横向我们算法的运行情况。

上面是一个可用的损失函数的定义。计算预测值于实际值得方差来量化算法运行质量。
但在逻辑回归中并不会这么做，因为他是一个非凸函数，有多个低谷，导致多个局部最优解。
我们希望损失函数是凸函数，如下，只有一个最优解：

得如下损失函数。

这是计算一个样本的损失函数，但训练数据集很大，需要一个全局的损失函数，也叫成本函数，如下：

逻辑回归与梯度下降算法

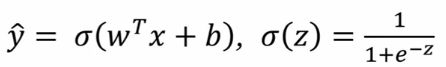
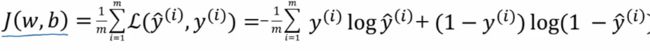
已知逻辑回归算法的公式，全局成本函数来评价算法运行的情况。
现需一个方法来 迭代式地训练 学习到w和b的值，并用成本函数来判断哪个w和b是最优解(学习特征权重)。
不停变换w和b的值并用成本函数计算预测值和实际值，找到差距最小，即成本函数值最小的一组w和b。

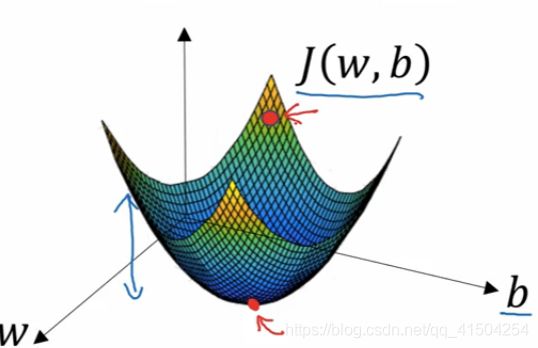
上图为成本函数，是一个凸函数，只有一个最优解。
初始化一个w和b的值(通常是0), 即图中最上面的红点。
不断迭代，每一次迭代都减少w和b的值让红点向下走，直到最下面的那个小红点，或者最接近那个小红点的地方，也就是我们找到全局最优解的地方。
有最小成本函数，预测值是最接近实际值。

在梯度下降算法中，不断减少w和b的值来迭代，增量[减小量]由以下公式得到：

假设求w的值，每次都用w自身减去α(学习率)和成本函数J对w的导数（即斜率）。
其中学习率是算法的参数，需要人工设定。

---

有了以上背景知识，再来看视频第三周部分代码好像就能理解一些了。
先导入三个需要的包

import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt

第一次遇到问题说 No module named matplotlib.pyplot
看网上的解决方法有的说 pip install matplotlib 没有用
需要 sudo apt-get install python-matplotlib
但我是 Mac 用的brew 找不到这个东西…
其实用 source activate tensorflow切换到tensorflow的路径下
再 pip install matplotlib 就OK了

#使用numpy来生成200个随机点
x_data = np.linspace(-0.5,0.5,200)[:,np.newaxis] #从-0.5～0.5的范围产生200个均匀分布的点，那么生成的是一维的，
                                                #生成的数据存在“：”处，后面是增加维度
noise = np.random.normal(0,0.02,x_data.shape)
y_data = np.square(x_data) + noise  #做的是一个非线性回归

#定义两个placeholder
x = tf.placeholder(tf.float32,[None,1]) #[None，1] 即行不确定，列为1列.形状不确定
y = tf.placeholder(tf.float32,[None,1])

构建一个神经网络，输入一个点x，经过一个神经网络的计算最后会得到一个预测值y
希望预测值和真实的y比较接近
输入层只有一个点所以只有一个神经元
中间层可以调整，假设使用10个神经元
输出层也只有一个神经元

#定义神经网络中间层
Weight_L1=tf.Variable(tf.random_normal([1,10])) #权值，连接输入层和中间层，一行[输入层]十列[中间层]
biases_L1=tf.Variable(tf.zeros([1,10]))         #偏置值
Wx_plus_b_L1 = tf.matmul(x,Weight_L1) + biases_L1 #输入为x  tf.matmul():矩阵的乘积
L1 = tf.nn.tanh(Wx_plus_b_L1)                   #L1为中间层的输出，tanh()为双曲正切函数作为接口函数

#定义输出层[输出层的输入相当于中间层的输出]
Weight_L2= tf.Variable(tf.random_normal([10,1])) #连接中间层和输出层，十行[中间层]一列[输出层]
biases_L2 = tf.Variable(tf.zeros([1,1]))
Wx_plus_b_L2=tf.matmul(L1,Weight_L2)+biases_L2 #[输出层的输入相当于中间层的输出]即 L1
prediction =  tf.nn.tanh(Wx_plus_b_L2) #tanh()为双曲正切

tanh()为双曲正切函数，是上文提到的激活函数之一

tf.nn :提供神经网络相关操作的支持,包括卷积操作(conv)、池化操作(pooling)、归一化、loss、分类操作、embedding、RNN、Evaluation

#二次代价函数
loss = tf.reduce_mean(tf.square(y-prediction))
#使用梯度下降法训练
train_step = tf.train.GradientDescentOptimizer(0.1).minimize(loss)

with tf.Session() as sess:
    #变量初始化
    sess.run(tf.global_variables_initializer())
    for _ in range(2000):
        sess.run(train_step,feed_dict={x:x_data,y:y_data})
   
    #获得预测值
    prediction_value=sess.run(prediction,feed_dict={x:x_data})
    #画图
    plt.figure()
    plt.scatter(x_data,y_data)
    plt.plot(x_data,prediction_value,'r-',lw=5)
    plt.show()

画出来的效果如下：

蓝色的点即为随机生成的200个样本点
红线为神经网络训练好生成的， 是距离点最小的线

---

最后粘一些这次的参考

深度学习基础知识04-二分类问题 by 小鑫的代码日常
深度学习基础–二分类 by 孙高飞
【深度学习框架TensorFlow】零基础入门|应用