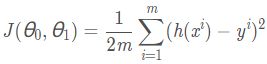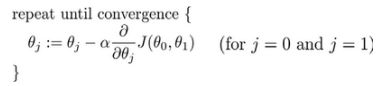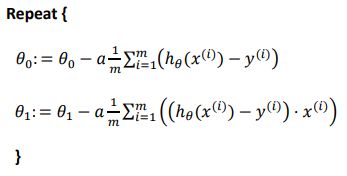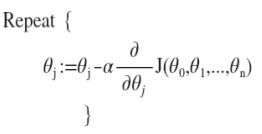吴恩达机器学习笔记（一）

一. 引言

1. 什么是机器学习

机器学习（Machine Learning）：是研究计算机怎样模拟或实现人类的学习行为，以获取新的知识或技能，重新组织已有的知识结构使之不断改善自身的性能。一个程序被认为能从经验E中学习，解决任务 T，达到性能度量值P，当且仅当，有了经验E后，经过P评判， 程序在处理T时的性能有所提升。

2. 监督学习和无监督学习

（1）监督学习（Supervised Learning）

对于数据集中每一个样本都有对应的标签。

我们给学习算法一个数据集。这个数据集由“正确答案”组成，然后运用学习算法，算出更多的正确答案。

回归（regression）：我们在试着推测出这一系列连续值属性。（e.g.房价）

分类（classification）：我们试着推测出离散的输出值。（e.g.良性/恶性）

（2）无监督学习（Unsupervised Learning）

数据集中没有任何的标签。

聚类（clustering）：我们已知数据集，却不知如何处理，也未告知每个数据点是什么。针对数据集，无监督学习能判断出数据有两个（或多个）不同的聚集簇，把这些数据分成两个（或多个）不同的簇。（e.g.谷歌新闻）

鸡尾酒晚会：区分不同的声音
[W,s,v] = svd((repmat(sum(x.*x,1),size(x,1),1).*x)*x’);        //奇异值分解

Octave编程环境

二. 单变量线性回归

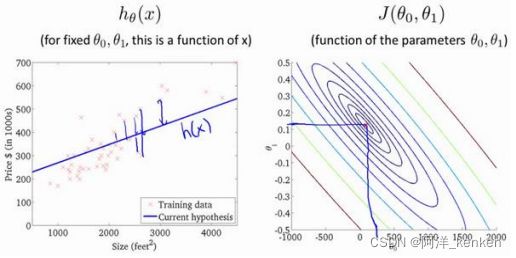
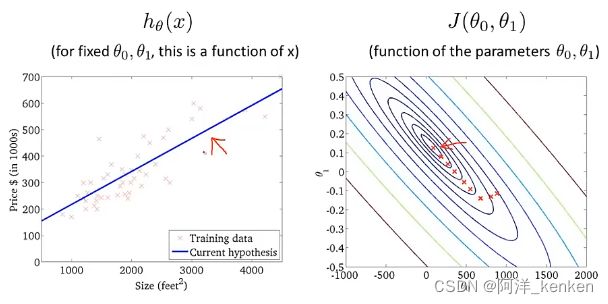
1. 模型表示

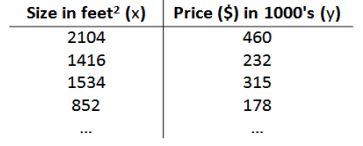
e.g. 回归问题的训练集（Training Set）

我们将要用来描述这个回归问题的标记如下：
代表训练集中实例的数量
代表特征/输入变量
代表目标变量/输出变量
(, ) 代表训练集中的实例
( () , () ) 代表第 个观察实例
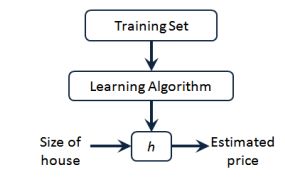
ℎ 代表学习算法的解决方案或函数也称为假设（hypothesis）函数

一种可能的表达方式为：ℎ () = 0 + 1
：模型参数

2. 代价函数

代价函数（cost function）J ( θ ) ，通常使用平方误差函数：

 我们的目标便是选择出可以使得建模误差的平方和能够最小的模型参数。

（1） 

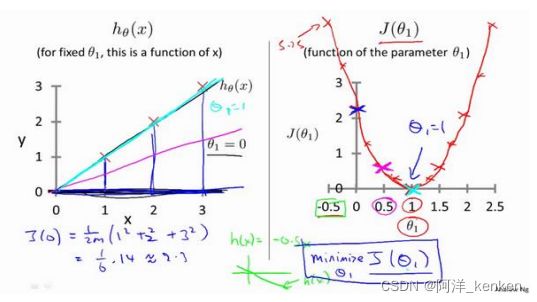
简化了公式，只包含 θ1，θ0为0，画出每个θ1对应的J (θ1)（二维），找到minimize J (θ1)

（2） 

 
包含θ0和θ1，用等高线图来表示（三维）

3. 梯度下降

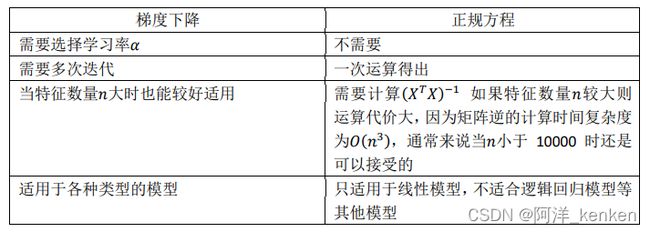
梯度下降是一个用来求函数最小值的算法。相比正规方程(normal equations)，梯度下降算法适用于更大数据集。

自动地找出能使代价函数最小化的参数0和1的值。（可以推广到0,1,…,n）

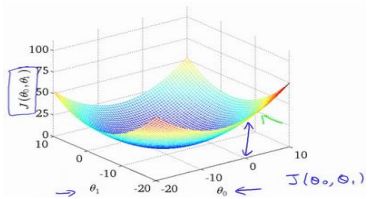
（1）思想：

开始时我们随机选择一个参数的组合(0, 1,…, )，计算代价函数，然后我们寻找下一个能让代价函数值下降最多的参数组合。我们持续这么做直到得到一个局部最小值（local minimum），因为我们并没有尝试完所有的参数组合，所以不能确定我们得到的局部最小值是否便是全局最小值（global minimum），选择不同的初始参数组合，可能会找到不同的局部最小值。

（2）公式：

批量梯度下降（batch gradient descent）算法的公式为：

:= 赋值        = 判断

其中是学习速率（learning rate），它决定了我们沿着能让代价函数下降程度最大的方向向下迈出的步子有多大，在批量梯度下降中，我们每一次都同时让所有的参数减去学习速率乘以代价函数的导数。

注意：同步更新所有参数

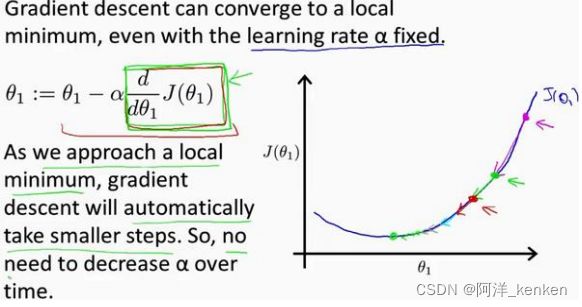
（3）理解

随着梯度下降法的运行，移动的幅度会自动变得越来越小，直到最终移动幅度非常小，收敛到局部极小值。 

（4）梯度下降的线性回归（应用）

梯度下降算法                                        线性回归模型

 
求导并改写算法

 
效果

 三. 多变量线性回归

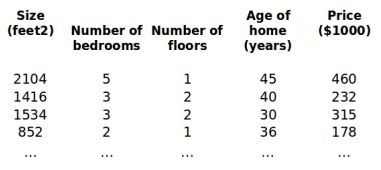
1. 多维特征

e.g.

增添更多特征后，我们引入一系列新的注释：
代表特征的数量
() 代表第 个训练实例，是特征矩阵中的第行，是一个向量（vector）。

支持多变量的假设函数 ℎ 表示为：ℎ () = 0 + 11 + 22+…+
这个公式中有 + 1个参数和个变量，为了使得公式能够简化一些，引入0 = 1，则公式转化为：ℎ () = 00 + 11 + 22+… +
即公式可以简化为：

2. 多变量梯度下降

梯度下降算法

 
求导并改写算法

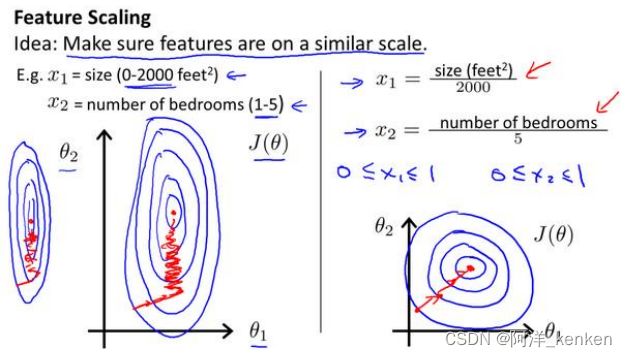
 （1）特征缩放

在我们面对多维特征问题的时候，我们要保证这些特征都具有相近的尺度，这将帮助梯度下降算法更快地收敛。

归一化前后迭代次数对比

 尝试将所有特征的尺度都尽量缩放到-1 到 1，不需要非常精确。

Mean normalization：

，其中 是平均值，是标准差

max-min：

（2）学习率α

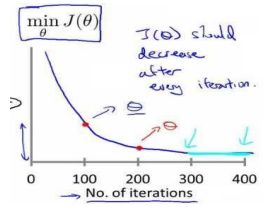
梯度下降算法收敛所需要的迭代次数根据模型的不同而不同，我们不能提前预知，我们可以绘制迭代次数和代价函数的图表来观测算法在何时趋于收敛。

也有一些自动测试是否收敛的方法，例如将代价函数的变化值与某个阀值（例如 0.001） 进行比较，但通常看上面这样的图表更好。

梯度下降算法的每次迭代受到学习率的影响，如果学习率过小，则达到收敛所需的迭代次数会非常高；如果学习率过大，每次迭代可能不会减小代价函数，可能会越过局部最小值导致无法收敛。

通常可以考虑尝试：α=…，0.01，0.03，0.1，0.3，1，3，10，…

3. 特征和多项式回归

线性回归并不适用于所有数据，有时我们需要曲线来适应我们的数据，比如一个二次方模型： 或三次方模型： 或：

通常我们需要先观察数据然后再决定准备尝试怎样的模型。

可以自由选择使用什么特征、什么函数拟合数据。之后会介绍如何使用算法判断。

4. 正规方程

正规方程是通过求解下面的方程来找出使得代价函数最小的参数的：

假设训练集特征矩阵为 （包含了 0 = 1），训练集结果为向量 ，则利用正规方程解出向量（矩阵X需可逆）

在Octave中，正规方程写作：pinv(X'*X)*X'*y

矩阵不可逆时：

（1）存在两个相关联的特征值：删除多余特征（存在线性关系）

（2）大量特征值（m <= n）：删除某些特征值、正则化

在Octave中使用pinv函数，即使矩阵X不可逆，也可以正确运行。