机器学习-时间序列
前言:
关于时间序列:我做了很多摸索探究,先不说深度学习吧,把机器学习玩6了吧
文章目录
- 预测质量评价指标
- 平滑
-
- 指数平滑
- 双指数平滑
- 时序的特征提取
-
- 时差
- 时间特征
- 目标编码
- 特征选择
- 深度学习
-
-
- 注意点
-
预测质量评价指标
R 平方: 可决系数,取值范围为 [ 0 , + ∞ ) [0, +\infty) [0,+∞) ,其值越大,表示拟合效果越好 调用接口为 sklearn.metrics.r2_score,计算公式如下:
R 2 = 1 − S S r e s S S t o t R^2 = 1 - \frac{SS_{res}}{SS_{tot}} R2=1−SStotSSres
平均绝对误差: 即所有单个观测值与算术平均值的偏差的绝对值的平均。这是一个可解释的指标,因为它与初始系列具有相同的计量单位。取值范围为 [ 0 , + ∞ ) [0, +\infty) [0,+∞) ,调用接口为 sklearn.metrics.mean_absolute_error ,计算公式如下:
M A E = ∑ i = 1 n ∣ y i − y ^ i ∣ n MAE = \frac{\sum\limits_{i=1}^{n} |y_i - \hat{y}_i|}{n} MAE=ni=1∑n∣yi−y^i∣
中值绝对误差: 与平均绝对误差类似,即所有单个观测值与算术平均值的偏差的绝对值的中值。而且它对异常值是不敏感。取值范围为 [ 0 , + ∞ ) [0, +\infty) [0,+∞) ,调用接口为 sklearn.metrics.median_absolute_error ,计算公式如下: M e d A E = m e d i a n ( ∣ y 1 − y ^ 1 ∣ , . . . , ∣ y n − y ^ n ∣ ) MedAE = median(|y_1 - \hat{y}_1|, ... , |y_n - \hat{y}_n|) MedAE=median(∣y1−y^1∣,...,∣yn−y^n∣)
均方差:最常用的度量标准,对大偏差给予较高的惩罚,反之亦然,取值范围为 [ 0 , + ∞ ) [0, +\infty) [0,+∞) ,调用接口为 sklearn.metrics.mean_squared_error ,计算公式如下: M S E = 1 n ∑ i = 1 n ( y i − y ^ i ) 2 MSE = \frac{1}{n}\sum\limits_{i=1}^{n} (y_i - \hat{y}_i)^2 MSE=n1i=1∑n(yi−y^i)2
均方对数误差: 这个与均方差类似,通过对均方差取对数而得到。因此,该评价指标也更重视小偏差。这指标通常用在呈指数趋势的数据。取值范围为 [ 0 , + ∞ ) [0, +\infty) [0,+∞) ,调用接口为 sklearn.metrics.mean_squared_log_error ,计算公式如下:
M S L E = 1 n ∑ i = 1 n ( l o g ( 1 + y i ) − l o g ( 1 + y ^ i ) ) 2 MSLE = \frac{1}{n}\sum\limits_{i=1}^{n} (log(1+y_i) - log(1+\hat{y}_i))^2 MSLE=n1i=1∑n(log(1+yi)−log(1+y^i))2
平均绝对百分比误差:这与 MAE 相同,但是是以百分比计算的。取值范围为 [ 0 , + ∞ ) [0, +\infty) [0,+∞) ,计算公式如下: M A P E = 100 n ∑ i = 1 n ∣ y i − y ^ i ∣ y i MAPE = \frac{100}{n}\sum\limits_{i=1}^{n} \frac{|y_i - \hat{y}_i|}{y_i} MAPE=n100i=1∑nyi∣yi−y^i∣
平均绝对百分比误差的实现如下:
def mean_absolute_percentage_error(y_true, y_pred):
return np.mean(np.abs((y_true - y_pred) / y_true)) * 100
导入上述的评价指标:
from sklearn.metrics import (mean_absolute_error, mean_squared_error,
mean_squared_log_error, median_absolute_error,
r2_score)
平滑
一般情况下,处理时间序列的核心任务就是根据历史数据来对未来进行预测。这可以通过许多模型来完成。先来介绍一个最老也是最简单的模型:移动平均。
在移动平均中,假设 y ^ t \hat{y}_{t} y^t 仅仅依赖 k k k 个最相近的值,对这 k k k 个值求平均值得到 y ^ t \hat{y}_{t} y^t 。公式如下式所示: y ^ t = 1 k ∑ n = 1 k y t − n \hat{y}_{t} = \frac{1}{k} \displaystyle\sum^{k}_{n=1} y_{t-n} y^t=k1n=1∑kyt−n
很明显,这种方法不能预测未来很久的数据。因为,为了预测下一个的值,就需要实际观察到之前的值。但这种方法可以对原始数据进行平滑。在进行平滑时,窗口越宽,也就是 k 的值越大,趋势越平滑。对于波动非常大的数据,这种处理可以使其更易于分析。
we try something!
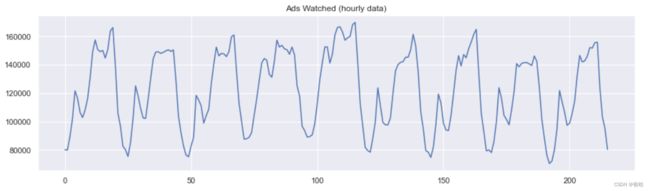
通过举个例子来进行说明,这里有一份真实的手机游戏数据,记录的是用户每小时观看的广告和每天游戏货币的支出
- 画图函数
def plotMovingAverage(
series, window, plot_intervals=False, scale=1.96, plot_anomalies=False
):
"""
series - 时间序列
window - 滑动窗口尺寸
plot_intervals -置信区间
plot_anomalies - 显示异常值
"""
rolling_mean = series.rolling(window=window).mean()
plt.figure(figsize=(15, 4))
plt.title("Moving average\n window size = {}".format(window))
plt.plot(rolling_mean, "g", label="Rolling mean trend")
# 画出置信区间
if plot_intervals:
mae = mean_absolute_error(series[window:], rolling_mean[window:])
deviation = np.std(series[window:] - rolling_mean[window:])
lower_bond = rolling_mean - (mae + scale * deviation)
upper_bond = rolling_mean + (mae + scale * deviation)
plt.plot(upper_bond, "r--", label="Upper Bond / Lower Bond")
plt.plot(lower_bond, "r--")
# 画出奇异值,upper_bond:上界 ,lowwer_bond下界
if plot_anomalies:
anomalies = pd.DataFrame(index=series.index, columns=series.columns)
anomalies[series < lower_bond] = series[series < lower_bond]
anomalies[series > upper_bond] = series[series > upper_bond]
plt.plot(anomalies, "ro", markersize=10)
plt.plot(series[window:], label="Actual values")
plt.legend(loc="upper left")
plt.grid(True)
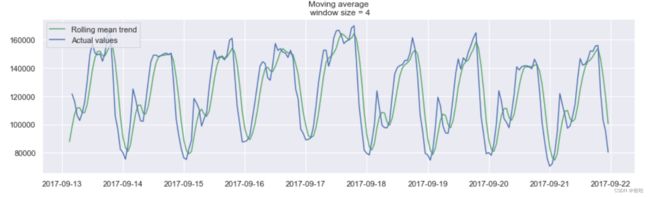
平滑的目的不是预测的有多准确,而是得到变化趋势,上图所示,是24小时(每天的趋势)
当对时间数据进行平滑时,可以清楚的看到整个用户查看广告的动态过程。在整个周末期间(2017-09-16),整个值变得很高,这是因为周末许多人都会有更多的时间。
- 给出置信区间
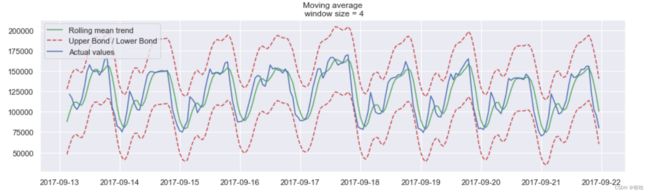
置信区间:【rolling_mean - (mae + scale * deviation),rolling_mean + (mae + scale * deviation)】
- 找出异常值
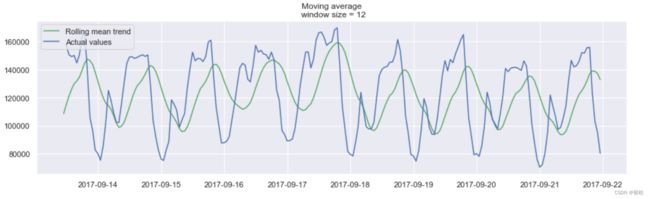
在这里的检测结果出乎意料,从图中可以看到该方法的缺点:它没有捕获数据中的每月季节性,并将几乎所有的峰值标记为异常。
指数平滑
与加权平滑不同,加权平滑只是加权时间序列最后的 k 个值,而 指数平滑 则是一开始加权所有可用的观测值,而当每一步向后移动窗口时,进行指数地减小权重,这个过程可以使用下面的公式进行表达。 y ^ t = α ⋅ y t + ( 1 − α ) ⋅ y ^ t − 1 \hat{y}_{t} = \alpha \cdot y_t + (1-\alpha) \cdot \hat y_{t-1} y^t=α⋅yt+(1−α)⋅y^t−1
这里,预测值是当前真实值和先前预测值之间的加权平均值。 权重称为平滑因子。它定义了预测将「忘记」最后一次可用的真实观测值的速度。 越小,先前观测值的影响越大,系列越平滑。
定义指数平滑的函数:
def exponential_smoothing(series, alpha):
"""
series - 时间序列
alpha - 平滑因子
"""
result = [series[0]] # 第一个值是一样的,存储平滑的结果
for n in range(1, len(series)):
result.append(alpha * series[n] + (1 - alpha) * result[n - 1])
return result
- 画图函数
def plotExponentialSmoothing(series, alphas):
"""
画出不同 alpha 值得平滑结果
series - 时间序列
alphas - 平滑因子
"""
with plt.style.context("seaborn-white"):
plt.figure(figsize=(15, 4))
for alpha in alphas:
plt.plot(
exponential_smoothing(series, alpha), label="Alpha {}".format(alpha)
)
plt.plot(series.values, "c", label="Actual")
plt.legend(loc="best")
plt.axis("tight")
plt.title("Exponential Smoothing")
plt.grid(True)
α = 0.3 / 0.05 \alpha=0.3/0.05 α=0.3/0.05
双指数平滑
为了提取更多细节信息,将时间序列数据分解为两个分量:截距(即水平) ℓ 和斜率(即趋势) 。对于截距,可以使用之前所述的平滑方法进行平滑,对于趋势,则假设时间序列的趋势(未来方向变化)取决于先前值的加权变化,对趋势应用相同的指数平滑。因此,可以使用以下函数来表示
在上面的式子中,
- 第一个函数是截距计算公式,其中的第一项取决于序列的当前值;第二项现在分为以前的水平和趋势值。
- 第二个函数描述趋势,它取决于当前时间点的水平变化和趋势和先前值。在这种情况下, 系数是指数平滑的权重。
- 第三个函数描述的最终预测是截距和趋势的总和。
def double_exponential_smoothing(series, alpha, beta):
"""
series - 序列数据
alpha - 取值范围为 [0.0, 1.0], 水平平滑参数
beta - 取值范围为 [0.0, 1.0], 趋势平滑参数
"""
# 原始序列和平滑序列的第一个值相等
result = [series[0]]
for n in range(1, len(series) + 1):
if n == 1:
level, trend = series[0], series[1] - series[0]
if n >= len(series): # 预测
value = result[-1]
else:
value = series[n]
last_level, level = level, alpha * value + (1 - alpha) * (level + trend)
trend = beta * (level - last_level) + (1 - beta) * trend
result.append(level + trend)
return result
结果:
从上面的图可以看出,可以通过调整两个参数 和 来得到不同的结果。 负责序列的平滑, 负责趋势的平滑。值越大,最近观测点的权重越大,模型系列的平滑程度越小。某些参数组合可能会产生奇怪的结果,尤其是手动设置时。
三指数平滑:
你可能已经猜到了,这个想法是增加第三个组成部分:季节性成分。这意味着如果时间序列预计没有季节性,就不应该使用这种方法。模型中的季节性成分将解释围绕截距和趋势的重复变化,并且将通过季节的长度来指定,换言之,通过变化重复的时段来指定。对于季节中的每个观测值,都有一个单独的组成部分,例如,如果季节的长度为 7 天(每周季节性),则有 7 个季节性成分,也即是一周中的每一天。
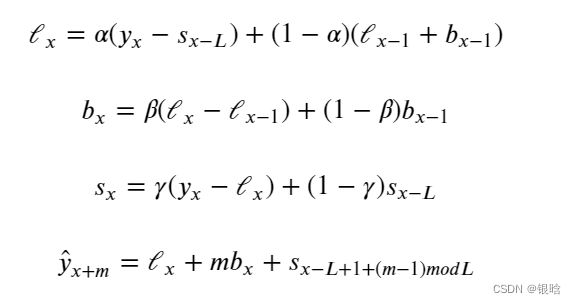
截距现在取决于序列的当前值减去相应的季节性成分。而趋势保持不变,季节性分量取决于系列的当前值减去截距和其先前值。考虑到所有可用季节的成分都是平滑的,例如,如果我们有星期一季节性成分,那么它只会与其他星期一平均。
你可以阅读更多关于 平滑参考资料如何工作以及如何完成趋势和季节性成分的初始近似。有了季节性因素,模型不仅可以预测未来的一两步,而且还可以预测未来任意的 步,这听起来挺nb的。
三次指数平滑模型也称为 Holt-Winters 模型,得名于发明人的姓氏 Charles Holt 和他的学生 Peter Winters。此外,模型中还引入了 Brutlag 方法,用来创建置信区间,其公式描述如下:

其中 T T T 是季节的长度, d d d 是预测的偏差。其他参数取自三指数平滑。想要了解更多细节的内容,可以参考 这篇论文。
- 实现起来非常复杂,我实现不出来了,CV了一下大佬的代码
class HoltWinters:
def __init__(self, series, slen, alpha, beta, gamma, n_preds, scaling_factor=1.96):
self.series = series
self.slen = slen
self.alpha = alpha
self.beta = beta
self.gamma = gamma
self.n_preds = n_preds
self.scaling_factor = scaling_factor
def initial_trend(self):
sum = 0.0
for i in range(self.slen):
sum += float(self.series[i + self.slen] - self.series[i]) / self.slen
return sum / self.slen
def initial_seasonal_components(self):
seasonals = {}
season_averages = []
n_seasons = int(len(self.series) / self.slen)
# 计算季节平均值
for j in range(n_seasons):
season_averages.append(
sum(self.series[self.slen * j : self.slen * j + self.slen])
/ float(self.slen)
)
# 计算初始值
for i in range(self.slen):
sum_of_vals_over_avg = 0.0
for j in range(n_seasons):
sum_of_vals_over_avg += (
self.series[self.slen * j + i] - season_averages[j]
)
seasonals[i] = sum_of_vals_over_avg / n_seasons
return seasonals
def triple_exponential_smoothing(self):
self.result = []
self.Smooth = []
self.Season = []
self.Trend = []
self.PredictedDeviation = []
self.UpperBond = []
self.LowerBond = []
seasonals = self.initial_seasonal_components()
for i in range(len(self.series) + self.n_preds):
if i == 0: # 季节性成分初始化
smooth = self.series[0]
trend = self.initial_trend()
self.result.append(self.series[0])
self.Smooth.append(smooth)
self.Trend.append(trend)
self.Season.append(seasonals[i % self.slen])
self.PredictedDeviation.append(0)
self.UpperBond.append(
self.result[0] + self.scaling_factor * self.PredictedDeviation[0]
)
self.LowerBond.append(
self.result[0] - self.scaling_factor * self.PredictedDeviation[0]
)
continue
if i >= len(self.series): # 预测
m = i - len(self.series) + 1
self.result.append((smooth + m * trend) + seasonals[i % self.slen])
# 在预测时,增加一些不确定性
self.PredictedDeviation.append(self.PredictedDeviation[-1] * 1.01)
else:
val = self.series[i]
last_smooth, smooth = (
smooth,
self.alpha * (val - seasonals[i % self.slen])
+ (1 - self.alpha) * (smooth + trend),
)
trend = self.beta * (smooth - last_smooth) + (1 - self.beta) * trend
seasonals[i % self.slen] = (
self.gamma * (val - smooth)
+ (1 - self.gamma) * seasonals[i % self.slen]
)
self.result.append(smooth + trend + seasonals[i % self.slen])
# 偏差按Brutlag算法计算
self.PredictedDeviation.append(
self.gamma * np.abs(self.series[i] - self.result[i])
+ (1 - self.gamma) * self.PredictedDeviation[-1]
)
self.UpperBond.append(
self.result[-1] + self.scaling_factor * self.PredictedDeviation[-1]
)
self.LowerBond.append(
self.result[-1] - self.scaling_factor * self.PredictedDeviation[-1]
)
self.Smooth.append(smooth)
self.Trend.append(trend)
self.Season.append(seasonals[i % self.slen])
参数:
- series - 时间序列
- slen - 季节长度
- alpha, beta, gamma - 三指数模型系数
- n_preds -预测
- scaling_factor -置信值设置
时间序列交叉验证很简单,我们在时间序列的一小部分上训练模型,从开始到时间节点 ,对下一个 + 时刻进行预测,并计算误差。然后,将训练样本扩展到 + 值,从 + 做出预测,直到 +2∗ ,并继续移动时间序列的测试段,直到达到最后一次可用的观察。因此,在初始训练样本和最后一次观察之间,可以得到与 一样多的数据份数。
- 也就是说,一段一段的移动,一段一段的数据作为测试集
data = ads.Ads[:-20] # 留下一些数据用于测试
# 初始化模型的参数
x = [0, 0, 0]
# 最小化损失函数
opt = minimize(
timeseriesCVscore,
x0=x,
args=(data, mean_squared_log_error),
method="TNC",
bounds=((0, 1), (0, 1), (0, 1)),
)
# 取出最优的参数
alpha_final, beta_final, gamma_final = opt.x
print(alpha_final, beta_final, gamma_final)
# 使用最优参数训练模型
model = HoltWinters(
data,
slen=24,
alpha=alpha_final,
beta=beta_final,
gamma=gamma_final,
n_preds=50,
scaling_factor=3,
)
model.triple_exponential_smoothing()
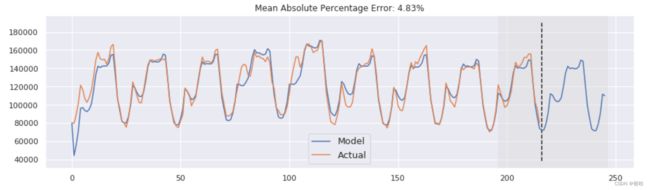
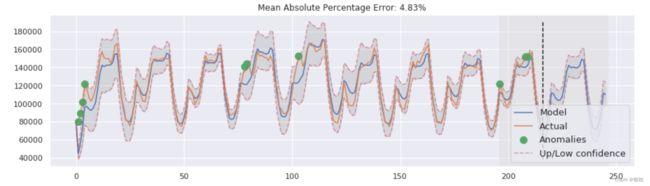
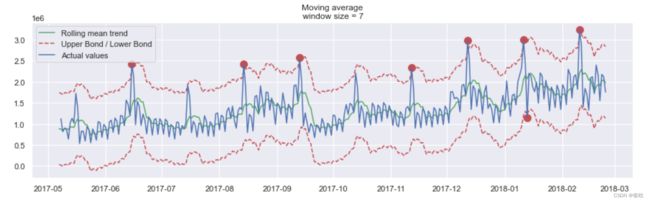
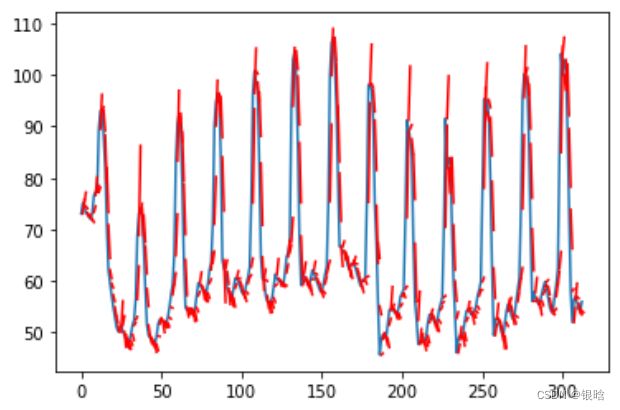
从图中可以看出,模型能够成功地拟合原始的时间序列,并捕捉到了每日季节性和整体向下趋势,甚至一些异常也检测到了。如果你看模型的偏差,你可以清楚地看到模型对序列结构的变化作出了相当大的反应,但随后迅速将偏差返回到正常值,基本上是「遗忘」掉过去。该模型的这一特性使我们能够快速构建异常检测系统,即使对于嘈杂的系列数据,也不需要花费太多时间和精力来准备数据和训练模型
时序的特征提取
- 时序的时差
- 窗口统计:
- 序列在一个窗口中的最大最小值
- 一个窗口中的中值和平均值
- 窗口的方差
- 等等
- 时间特征:
- 年月日,时分秒
- 假期、特殊的节日
- 目标编码
- 其他模型的预测结果
画图函数:
def plotModelResults(
model, X_train=X_train, X_test=X_test, plot_intervals=False, plot_anomalies=False
):
"""
画出模型、事实值、预测区间和异常值的图表
"""
prediction = model.predict(X_test)
plt.figure(figsize=(15, 4))
plt.plot(prediction, "g", label="prediction", linewidth=2.0)
plt.plot(y_test.values, label="actual", linewidth=2.0)
if plot_intervals:
cv = cross_val_score(
model, X_train, y_train, cv=tscv, scoring="neg_mean_absolute_error"
)
mae = cv.mean() * (-1)
deviation = cv.std()
scale = 1.96
lower = prediction - (mae + scale * deviation)
upper = prediction + (mae + scale * deviation)
plt.plot(lower, "r--", label="upper bond / lower bond", alpha=0.5)
plt.plot(upper, "r--", alpha=0.5)
if plot_anomalies:
anomalies = np.array([np.NaN] * len(y_test))
anomalies[y_test < lower] = y_test[y_test < lower]
anomalies[y_test > upper] = y_test[y_test > upper]
plt.plot(anomalies, "o", markersize=10, label="Anomalies")
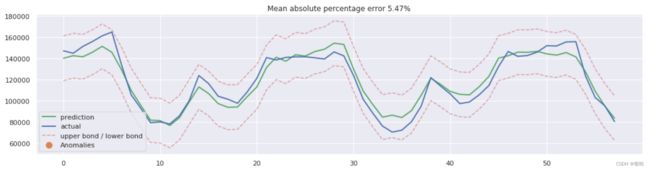
error = mean_absolute_percentage_error(prediction, y_test)
plt.title("Mean absolute percentage error {0:.2f}%".format(error))
plt.legend(loc="best")
plt.tight_layout()
plt.grid(True)
特征重要度可视化:
def plotCoefficients(model):
"""绘制模型的排序系数值
"""
coefs = pd.DataFrame(model.coef_, X_train.columns)
coefs.columns = ["coef"]
coefs["abs"] = coefs.coef.apply(np.abs)
coefs = coefs.sort_values(by="abs", ascending=False).drop(["abs"], axis=1)
plt.figure(figsize=(15, 4))
coefs.coef.plot(kind="bar")
plt.grid(True, axis="y")
plt.hlines(y=0, xmin=0, xmax=len(coefs), linestyles="dashed")
时差
- 直接对时间序列进行差分
时间特征
- 现在提取更多的特征,添加小时、日期、是否是周末等特征值。
目标编码
- 一种编码类别特征的版本: 按平均值编码。按平均值编码指的是用目标变量的平均值进行编码
- 日和、周和、月和…
特征选择
用模型来回归选择
- 岭回归
- LASSO
- XGBOOST…
深度学习
- RNN
- LSTM
- etc…
原理你自己get吧,我用tensorflow简单的玩一会lstm
#导入深度学习包
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import LSTM , Dense ,Dropout
from sklearn.preprocessing import MinMaxScaler
from keras.wrappers.scikit_learn import KerasRegressor
test_split = round(len(df1)*0.20)
test_split
#切分数据,切记不可随机打乱,而是有顺序的切分
test_split = round(len(df1)*0.20)
df_for_training = df1[:-312]
df_for_testing = df1[-312:]
#缩放数据,归一化
scaler = MinMaxScaler(feature_range=(0,1))
df_for_training_scaler = scaler.fit_transform(df_for_training)
df_for_testing_scaler = scaler.transform(df_for_testing)
df_for_training_scaler
#构造时间步,返回3维数据集(样本数,时间步,属性维度)
def createXY(dataset,n_past):
dataX=[]
dataY=[]
for i in range(n_past,len(dataset)):
dataX.append(dataset[i-n_past:i,0:dataset.shape[1]])
dataY.append(dataset[i,0])
return np.array(dataX),np.array(dataY)
trainX,trainY = createXY(df_for_training_scaler,3)
testX,testY = createXY(df_for_testing_scaler,3)
from sklearn.model_selection import GridSearchCV
#定义模型
def build_model(optimizer):
grid_model = Sequential()
grid_model.add(LSTM(50,return_sequences=True,input_shape=(3,13))) #第一层50个神经元
#中间的参数自己设置,我这仅供参考,神经元不是越多越好,估量一下参数的数量哦!
grid_model.add(LSTM(50))#第二层50个神经元
grid_model.add(Dropout(0.2))#损失降到0.2一下退出
grid_model.add(Dense(1)) #输出一个时间步
grid_model.compile(loss='mse',optimizer=optimizer)#评估指标与优化器
return grid_model
grid_model = KerasRegressor(build_fn=build_model,verbose=1,validation_data=(testX,testY))
#定义评价指标
def mape(true,predictd):
inside_sum = np.abs(predictd-true)/true
return round(100*np.sum(inside_sum)/inside_sum.size,2)
#r2_score
from sklearn.metrics import r2_score,mean_squared_error
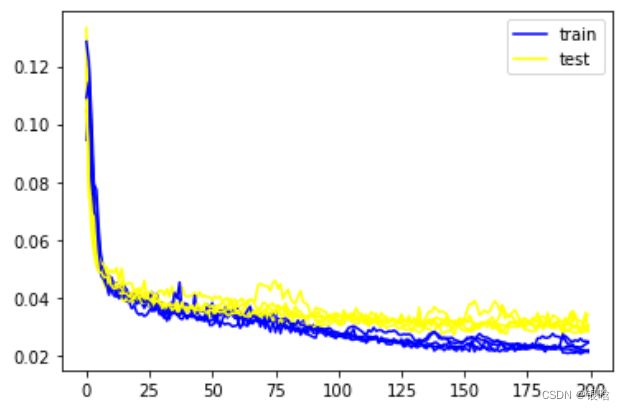
那么我根据具体需求更改一下时间步呢?
- 这是t+n的逐步输出,细节化
注意点
- 结果不好不要怪模型,模型很棒,是你的问题好吧!!!
- 数据和特征工程决定模型的高下,别怪模型+1
- 数据预处理应该占用你50%的时间,有因就有果,中间漏了啥,自己积累一些经验
- 机器学习,可不一定输给深度学习,
没有免费的午餐定理可以解释
XGBOOST在时序问题的表现,一点不弱呀!! 关键是还具有可解释性嘞
- 准确率score= 0.961624695892833
- 均方根误差rmse= 3.086622697986724
- 均方误差mse= 9.527239679726847