Lasso回归系列二:Lasso回归/岭回归的原理
Lasso回归/岭回归的原理
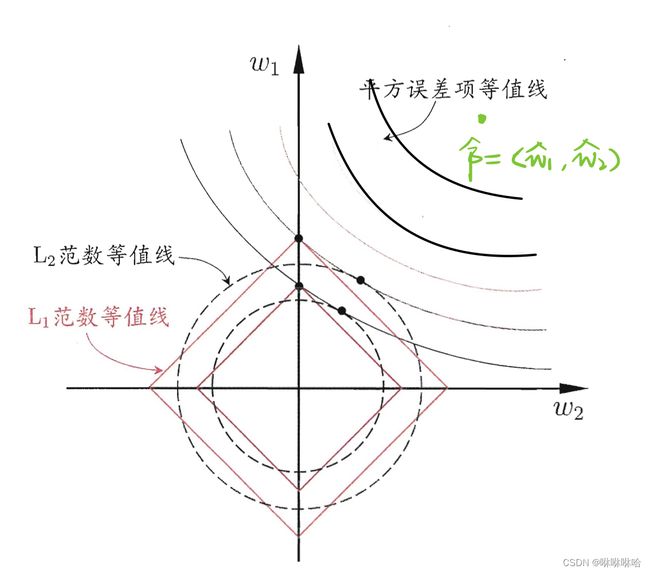
在学习L1,L2正则化的作用和区别时,我们总是会看到这样的一副图片:

这幅图片形象化地解释了L1,L2对线性模型产生的不同的约束效果。
我最开始其实是不太理解为什么要这么画的。比如
1、L1范数(L1-norm)等值线一定会和平方误差项等值线相交于某一坐标轴吗?
2、Lasso回归只能用平方和误差作为损失吗,换成交叉熵可以吗?
3、除了L1-norm,L2-norm,还有没有别的正则化方法,他们的区别是什么?
见我的另一篇博客Lasso回归系列三:机器学习中的L0, L1, L2, L2,1范数
现在算是搞明白了,结合网上很不错的几篇博客,再梳理一下,分享给大家,如有不足或者错误,请多多指正。
概述
使用L1正则化项的回归模型被称作Lasso回归(Lasso Regression),使用L2正则化项的回归模型被称作岭回归(Ridge Regression)。
所以只要是回归问题中加入L1正则项,都可以称为Lasso回归,并非只限于使用平方和误差作损失的情况。
在本文中,首先,我们会了解在使用最小二乘估求解线性回归问题时,加入L1-norm的Lasso回归,加入L2-norm的岭回归会使求解发生哪些变化,从而更好地理解如何使用Lasso回归和岭回归。
线性模型的最小二乘估
在对线性模型进行参数估计时,可以使用最小二乘法。
用数学语言来描述,线性模型可以表示为:
y = X β + ϵ E ( ϵ ) = 0 , C o v ( ϵ ) = σ 2 I y = X\beta +\epsilon \\E(\epsilon)=0, Cov(\epsilon) = \sigma^2 I y=Xβ+ϵE(ϵ)=0,Cov(ϵ)=σ2I
其中 y y y 是 n × 1 n \times 1 n×1的标签向量, X X X 是 n × p n \times p n×p的特征矩阵(对应到数据上, n n n是样本数, p p p是特征数量) , β \beta β , ϵ \epsilon ϵ是要估计的参数, β \beta β 是 p × 1 p \times 1 p×1的未知参数向量, ϵ \epsilon ϵ 是随机误差。
最小二乘法是估计参数向量 β \beta β 的基本方法,其思想是让误差尽可能得小,也即$\epsilon = y- X\beta $ 尽可能得小,也即是使
Q ( β ) = ∣ ∣ ϵ ∣ ∣ 2 = ∣ ∣ y − X β ∣ ∣ 2 = ( y − X β ) T ( y − X β ) Q(\beta) = ||\epsilon||^2 = ||y-X\beta||^2 = (y-X\beta)^T(y-X\beta) Q(β)=∣∣ϵ∣∣2=∣∣y−Xβ∣∣2=(y−Xβ)T(y−Xβ)
尽可能得小。
根据凸函数极小值就是最小值的定理,我们可以通过求得偏导等于0处的 β \beta β 值,使得上式达到最小值,即: rank(X)<p rank(X)<p
β ^ = ( X T X ) − 1 X T y \hat\beta = (X^TX)^{-1}X^Ty β^=(XTX)−1XTy
结合矩阵论中的知识,当 r a n k ( X ) = p rank(X)=p rank(X)=p 时, X T X X^TX XTX 可逆,这时 β \beta β 有唯一解,$\hat\beta = \beta $,称 $ \hat\beta $ 是 $ \beta $ 的无偏估计;当 r a n k ( X ) < p rank(X)
Lasso回归和Ridge回归
Lasso回归(lasso regression)是在目标函数后加一个权重 β \beta β 的1-范数(机器学习中的范数定义不同于数学中的定义,具体定义请看【https://xiongyiming.blog.csdn.net/article/details/81673491】),即:
Q ( β ) = ∣ ∣ y − X β ∣ ∣ 2 2 + λ ∣ ∣ β ∣ ∣ 1 ⟺ arg min ∣ ∣ y − X β ∣ ∣ 2 s . t . ∑ ∣ β j ∣ ≤ s Q(\beta) = ||y-X\beta||^2_2 + \lambda ||\beta||_1 \\ \quad \iff \\ \arg \min ||y-X\beta||^2 \quad s.t. \sum |\beta_j| \leq s Q(β)=∣∣y−Xβ∣∣22+λ∣∣β∣∣1⟺argmin∣∣y−Xβ∣∣2s.t.∑∣βj∣≤s
岭回归(ridge regression)是在目标函数后加一个权重 β \beta β 的2-范数,即:
Q ( β ) = ∣ ∣ y − X β ∣ ∣ 2 2 + λ ∣ ∣ β ∣ ∣ 2 ⟺ arg min ∣ ∣ y − X β ∣ ∣ 2 s . t . ∑ β j 2 ≤ s Q(\beta) = ||y-X\beta||^2_2 + \lambda ||\beta||_2 \\ \quad \iff \\ \arg \min ||y-X\beta||^2 \quad s.t. \sum \beta_j^2 \leq s Q(β)=∣∣y−Xβ∣∣22+λ∣∣β∣∣2⟺argmin∣∣y−Xβ∣∣2s.t.∑βj2≤s
对上式求解,可以得到 β \beta β 的岭估计:
β ^ ( λ ) = ( X T X + λ I ) − 1 X T y \hat\beta(\lambda) = (X^TX+\lambda I)^{-1}X^Ty β^(λ)=(XTX+λI)−1XTy
这样确保 X T X + λ I X^TX+\lambda I XTX+λI 满秩,可逆,当然此时的 β ^ ( λ ) \hat\beta(\lambda) β^(λ) 是一个有偏估计。
Lasso回归为什么更容易产生稀疏解?
我们再看下这幅图:
平方误差等值线即 Q ( β ) = ∣ ∣ y − X β ∣ ∣ 2 Q(\beta) = ||y-X\beta||^2 Q(β)=∣∣y−Xβ∣∣2 对应的等势线
Lasso回归对应L1范数等值线,Ridge回归对应L2范数等值线,两者均通过正则项参数 λ \lambda λ 来调节对参数 β \beta β 的约束程度。
Lasso回归容易产生稀疏解,是因为L1范数包含了一些在坐标轴上的不可微的角点(non-differentiable corner ),这些角点和 Q ( β ) = ∣ ∣ y − X β ∣ ∣ 2 Q(\beta) = ||y-X\beta||^2 Q(β)=∣∣y−Xβ∣∣2 相交的概率会大很多。而在Ridge回归中,L2范数是处处可微的,所以和 Q ( β ) = ∣ ∣ y − X β ∣ ∣ 2 Q(\beta) = ||y-X\beta||^2 Q(β)=∣∣y−Xβ∣∣2在坐标轴上相交的概率会小很多。
此外,对于L1范数来说, λ \lambda λ 越大, ∣ ∣ β ∣ ∣ 1 ||\beta||_1 ∣∣β∣∣1 的范围越小,平方误差等值线和L1范数等值线在坐标轴上相交的概率就越大,也就是说 β \beta β 中的元素变成0的概率越大。反之, β \beta β 中的元素变成0的概率则越小。
参考
L1,L2正则化方法
Lasso—原理及最优解