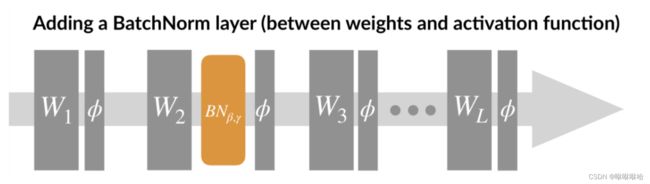
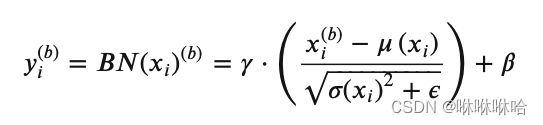Batch Normalization的原理和作用
机器学习高频面试问题—Batch Normalization
论文链接
Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift(Machine Learning 2015)
BN是什么
在神经网络中,每一层的输出是下一层的输入,神经网络通过反向传播调整参数。但是我们知道在反向传播的过程中,每一层的参数根据前一层参数变化前的输出进行参数的调整,区别于SVM这些有固定输入的模型,这就导致神经网络每层参数的更新和输入的更新之间存在一个延迟(Internal Covariate Shift)。对于深层模型来说,每层的输入和权重在同时变化,这样的训练相对困难。
为了避免震荡,不得不把学习率设置得足够小,但足够小又意味着学习的缓慢。为此,希望对每层输入的分布有所控制,于是就有了Batch Normalization,其出发点是对每层的输入做Normalization,只有一个数据是谈不上Normalization的,所以是对一个batch的数据进行Normalization。
论文中给出了BN的主要步骤:
其操作可以分成2步:
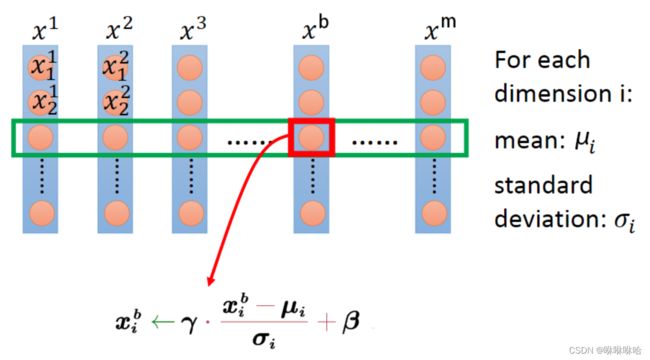
- Standardization:首先对个进行 Standardization,得到 zero mean unit variance的分布̂ 。
- scale and shift:然后再对̂ 进行scale and shift,缩放并平移到新的分布,具有新的均值方差。
其中, x i b x_i^b xib表示输入当前batch的 − t h -th b−th样本时该层 − t h -th i−th输入节点的值, _ xi为 [ 1 , 2 , … , ] [^1_,^2_,…,^_] [xi1,xi2,…,xim]构成的行向量,长度为batch size m,Font metrics not found for font: .和Font metrics not found for font: .为该行的均值和标准差,Font metrics not found for font: .为防止除零引入的极小量(可忽略),Font metrics not found for font: .和Font metrics not found for font: .为该行的scale和shift参数,可知
-
Font metrics not found for font: .和Font metrics not found for font: .为当前行的统计量,不可学习。
-
Font metrics not found for font: .和Font metrics not found for font: .为待学习的scale和shift参数,用于控制 _ yi的方差和均值。
-
BN层中, _ xi和 _ xj之间不存在信息交流 ( ≠ ) (≠) (i=j)
为什么要有第2步 scale and shift 呢?
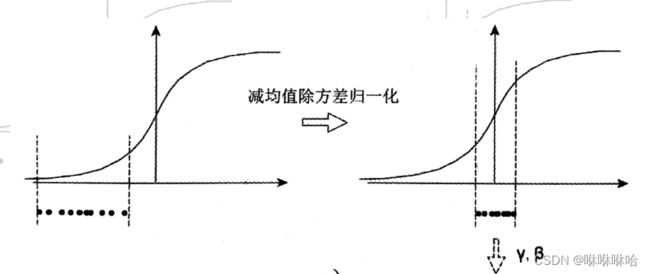
我们思考一个问题,在第1步中,减均值除方差得到的分布是正态分布,我们能否认为正态分布就是最好或最能体现我们训练样本的特征分布呢?不能,比如数据本身就很不对称(不符合正态分布),或者激活函数未必是对方差为1的数据最好的效果,比如Softmax激活函数,在-1~1之间的函数的梯度不大,那么非线性变换的作用就不能很好的体现,换言之就是,减均值除方差操作后可能会削弱网络的性能!针对该情况,在第一步Standardazation之后加入scale and shift,如下图所示,这才算完成真正的batch normalization。
**BN的本质就是利用优化变一下方差大小和均值位置,并且保证新的分布还比较切合数据的真实分布,保证模型的非线性表达能力。**BN的极端的情况就是这两个参数等于mini-batch的均值和方差,那么经过batch normalization之后的数据和输入完全一样,当然一般的情况是不同的。
BN的作用
- **抑制梯度消失(**主要作用)
- 通常在激活函数之前使用BN,如上图所示,左图中的点是没有经过任何处理的输入数据,曲线是sigmoid函数,此时数据在sigmoid梯度很小的区域,那么梯度更新就会很慢,甚至陷入长时间的停滞。减均值除方差后,数据就被移到中心区域如右图所示,对于大多数激活函数而言,这个区域的梯度都是最大的或者是有梯度的(比如ReLU),这可以看做是一种对抗梯度消失的有效手段。对于一层如此,如果对于每一层数据都那么做的话,数据的分布总是在随着变化敏感的区域,相当于不用考虑数据分布变化了,这样训练起来更有效率。
- 加速优化过程(主要作用)
- 可以使用更大的学习率,训练过程更加稳定,极大提高了训练速度。
- 减小了参数初始化带来的影响
- 可以将bias置为0,因为Batch Normalization的Standardization过程会移除直流分量,所以不再需要bias。
- 对权重初始化不再敏感,通常权重采样自0均值某方差的高斯分布,以往对高斯分布的方差设置十分重要,有了Batch Normalization后,对与同一个输出节点相连的权重进行放缩,其标准差Font metrics not found for font: .也会放缩同样的倍数,相除抵消。
- 对权重的尺度不再敏感,理由同上,尺度统一由参数控制,在训练中决定。
4、具有一定的正则化作用(意外作用,有的实验证明并无此作用)
- Batch Normalization具有某种正则作用,不需要太依赖dropout,L1,L2等正则化方式,减少过拟合。
BN每次的mini-batch的数据都不一样,而每次的mini-batch的数据都会对moving mean和moving variance产生作用,可以认为是引入了噪声,这就可以认为是进行了data augmentation,而data augmentation被认为是防止过拟合的一种方法。因此,可以认为用BN可以防止过拟合。
BatchNorm和LayerNorm的区别
区别:BatchNorm是对batch内不同样本的同一特征进行归一化,LayerNorm是对同一样本的不同特征进行归一化。
举个栗子:
假设现在有一个二维矩阵(3x4),行对应batch,列对应特征(行数对应batch size,列数对应特征维度)
import numpy as np
a=np.array([
[-0.66676328, -0.95822262, 1.2951657 , 0.67924618],
[-0.46616455, -0.39398589, 1.95926177, 2.36355916],
[-0.39897415, 0.80353481, -1.46488175, 0.55339737]])
BatchNorm就是对这个二维矩阵的每一列做归一化,layernorm是对每一行做归一化。
BatchNorm:
bu = np.mean(a, axis=0)
bs = np.std(a, axis=0)
bn_a=(a-bu)/bs
output:
bu = [-0.51063399 -0.18289123 0.59651524 1.19873424]
bs = [0.11375677 0.7345602 1.48262696 0.82525645]
bn_a: [[-1.37248351 -1.05550422 0.47122471 -0.62948682]
[ 0.39091691 -0.28737557 0.91914323 1.41147025]
[ 0.9815666 1.34287979 -1.39036794 -0.78198343]]
LayerNorm:
lu = np.mean(a, axis=1)
ls = np.std(a, axis=1)
ls_a = (a-lu[...,None])/ls[...,None]
lu = [ 0.0873565 0.86566762 -0.12673093]
ls = [0.93154023 1.30385305 0.893411 ]
ls_a = [[-0.80954075 -1.12241971 1.29657224 0.63538822]
[-1.0214588 -0.96610083 0.83874034 1.14881929]
[-0.30472338 1.04125172 -1.49779981 0.76127147]]
BatchNorm要求batch内所有样本的特征要等长,且所有样本同一维特征含义要保持一致,所以更适合处理图片,而不适合处理变长数据,比如nlp里不同长度的句子。
LayerNorm则只在同一样本内计算该样本所有特征的均值方差,所以可以处理变长样本,而且不受batch中其他数据的影响。
BatchNorm可以不同的特征归一化,消除特征量纲,并且保留样本间的差异。
LayerNorm可以将样本归一化,并且保持特征之间的差异性。
参考链接
https://www.cnblogs.com/shine-lee/p/11989612.html
https://blog.csdn.net/qq_35290785/article/details/89322289
https://www.zhihu.com/question/275788133/answer/384198714