转置卷积 反卷积 PyTorch torch.nn.ConvTranspose2d() output_padding

转置卷积、又称反卷积其实是卷积的逆过程。卷积的过程通常会减小特征图的的大小，而转置卷积往往增大特征图的大小，一直以来对转置卷积的过程都不是很理解，最近认真学习了一下，在此分享。

卷积

卷积操作，输入是一个特征图i，参数padding(p)， stride(s)，kernel_size(k)，输出是卷积后得到的特征图o，输出的特征图大小

转置卷积

转置卷积是卷积的逆过程。在做的转置卷积的时候，我们同样会给转置卷积几个参数，如输入特征图i，p，k，s，分别对应padding，kernel_size，stride。

第一如何理解转置卷积是卷积的逆过程？假设卷积的输入为x，输出为y，而转置卷积作为卷积的逆过程，也就是说转置卷积的输入为y，输出为x。即

因此，给定转置卷积参数和输出a，我们相当于找到完成这样的过程

，同时。

故我们知道卷积的输入大小和输出大小的关系，因此我们可以计算出b的大小:

假设a=2,s=1,k=1,p=0，此时

因此可以推断出转置卷积的输出的大小是，因此过程就是对大小为2的进行转置卷积，得到大小为3的特征图。因此转置卷积是逆卷积这句话体现在转置卷积核卷积是互逆的。

第二、转置卷积也是卷积。当s=1时，根据转置卷积自身参数的信息计算出一组参数，利用这组参数对转置卷积的输入进行卷积，得到输出。

然后以这组参数为卷积的参数，对转置卷积的输入进行卷积得到转置卷积的输出。

第三、转置卷积有时候也叫分数步长的卷积。当转置卷积的时，对应的卷积的，因此也称为分数步长的卷积。

当时，根据转置卷积自身参数的信息计算出一组参数：

，

此时不能直接利用这组参数对转置卷积的输入进行卷积，而是要对输入进行处理，主要分为两步：

1. 在输入的每两个像素之间增加s-1个0
2. 在输入的底边和右边加入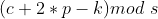，其中c就是根据第一步中计算出来的转置卷积输出的大小。

假设转置卷积的输入i=3,k=3,s=2,p=1，计算转置卷积的输出：

此时c有两种情况，当c=5时，，s-1=1，因此对的输入特诊图进行0填充，按第一步填充得到：

第二步中，故无需填充。

安照，计算出每个参数得到：

此时，再对特征图进行填充：

然后按照进行卷积得到结果

当c=6时，，s-1=1，因此对的输入特诊图进行0填充，按第一步填充得到：

第二步中，因此再在特诊图下面和右边填充一层

同样计算出参数，对特征图进行填充：

然后再卷积得到输出：

Pytorch中，

import torch.nn as nn

nn.ConvTranspose2d(in_channels=, out_channels=, kernel_size=, stride=, padding=, output_padding=)

PyTorch给出的官方文档： 

根据输入输出大小的计算公式，output_padding参数的设置就可以直接影响输出的大小，而上述部分计算转置卷积的输出的大小的时候，因为有向下取整操作，所以卷积输出的大小是不确定的。因此output_padding的设置正好可以除去这种不确定性。

比如在上面的例子中设置output_padding=0，对应第一种情况c=5，下面用代码验证，先设置output_padding=0

import torch.nn as nn
import torch

class TC(nn.Module):
    def __init__(self):
        super(TC, self).__init__()
        self.tc = nn.ConvTranspose2d(in_channels=3, out_channels=3, 
kernel_size=3, stride=2, padding=1,output_padding=0)

    def forward(self, x):
        return self.tc(x)


x = torch.zeros((1, 3, 3, 3))
print(x.shape)
tc = TC()
print(tc(x).shape)

输出：

修改output_padding=1，此时输出：

当然，设置的output_padding值不可以大于等于s(stride)，因为除了每个像素之间的填充以外，在特征图的下面和右边的填充是根据来计算的，是对s取余，output_padding值也正是设置的这一项，所以output_padding值不可以超过s。

参考文献https://github.com/vdumoulin/conv_arithmetic