Python手撸机器学习系列（二）：逻辑斯蒂回归（Logistic Regression）(附Python实现坐标点分类及鸢尾花分类)

一、原理

1.1 将回归变为分类

逻辑斯蒂回归是一个经典的二分类模型，它的精髓在于用线性回归做二分类（或多分类，本文以二分类为主）。线性回归的输出为没有约束的连续值，而分类在于0和1两个值，如何从回归值到分类值就需要一个映射，于是引入了sigmoid函数：
$$sigmoid(z)=\frac{1}{1+e^{-z}}$$
画出图像为：

即可以将回归输出映射到0-1之间。

我们的模型最后输出为：
$$f(x)=\frac{1}{1+e^{(-(W\cdot X+b)}}$$
这个值在0-1之间，代表模型的预测，根据分类的思维，我们可以将输出的值大于等于0.5的样本分类为1，小于0.5的分类为0。

同时，我们注意到，对于最后的输出，其实我们只需要判断$W\cdot X+b$的正负即可，因为当$W\cdot X+b\ge 0$时,对应的$f(x)\ge 0.5$，反之亦然。所以对于最后的预测，并不需要再经过$sigmoid$函数，只需要$W、b$参数即可。

一般情况下，为了便于实现，我们将$b$纳入$W$中，则$W$和$X$写作：
$$\begin{gathered} W=[b,w_1,w_2,...,w_n] \\ X=[1,x_1,x_2,...,x_n{]}^T \end{gathered}$$
在这里，$x_1,x_2,...,x_n$表示样本的特征个数,$w_1,w_2...,w_n$表示权值的个数（有多少特征就有多少个权重值），最后得到输出$out=b+w_1{x}_1+w_2{x}_2+...+w_n{x}_n$

当然$X$还可以写作多个样本以矩阵形式进行计算，即：
$$X=[X_1,X_2,...X_N]={\left[\begin{array}{cccc}1& x_{11}& \cdots & x_{1n}\\ 1& x_{21}& \cdots & x_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ 1& x_{N1}& \cdots & x_{Nn}\end{array}\right]}^T$$
这样$W\cdot X$就会得到$N$个值，$N$表示样本数量

1.2 目标函数的确立

接下来，我们需要考虑损失函数了。在之前的线性回归中，可以使用均方误差（MSE）做为损失。但在这里，sigmoid函数是非线性的，如果用MSE做损失函数，则会使损失函数变为非凸函数，形成许多的极小点，不易优化。于是引入如下的损失函数：
$$cost({\sigma }_W(x),y))=\{\begin{array}{ll}-log(h_W(x))& \text{y = 1}\\ & \\ -log(1-h_W(x))& \text{y = 0}\end{array}$$

损失函数即可变为凸函数进行优化，如下图所示：

这里的的$\sigma (\cdot )$即为$sigmoid$函数，合并来写就是：
$$cost({\sigma }_W(x),y)=-ylog({\sigma }_W(x)-(1-y)log(1-{\sigma }_W(x)))$$
将所有样本合起来，变称为最终的目标函数：
$$J(W)=-\frac{1}{m}\sum _{i=1}^m{y}_{i}log({\sigma }_W(x_i)+(1-y_i)log(1-{\sigma }_W(x_i)))$$
其中$m$为样本数量
这个目标函数是根据极大似然估计而推导而来的，具体如下节所示

1.2.1 极大似然估计求目标函数

原始模型的概率输出为：
$$\{\begin{array}{ll}{p}_1=P(y=1|x)=\frac{1}{1+e^{-W\cdot x}}& \text{y = 1}\\ & \\ p_2=P(y=0|x)=\frac{e^{-W\cdot x}}{1+e^{-W\cdot x}}& \text{y = 0}\end{array}$$
合并起来就是：
$$P(y|x)=p_1^y{p}_0^{1-y}$$
对$W$进行极大似然估计：

首先需要极大化似然函数：
$$L(W)=\prod _{i=1}^{m}p(y_i|x_i;W)=\prod _{i=1}^m{p}_1^{y_1}{p}_0^{1-y_1}=\prod _{i=1}^m({\sigma }_W(x_i){)}^{y_i}(1-{\sigma }_W(x_i){)}^{1-y_i})$$
两边同时取对数：
$$l(W)=logL(W)=\sum _{i=1}^m\left[y_{i}log({\sigma }_W(x_i))+(1-y_i)log(1-{\sigma }_W(x_i))\right]$$
最大化$l(W)$等于最小化$-l(W)$，且由于$m$是常数，所以进一步最小化函数$-\frac{1}{m}l(W)$，由此得到了逻辑斯蒂回归的最终目标函数：
$$J(W)=-\frac{1}{m}\sum _{i=1}^m{y}_{i}log({\sigma }_W(x_i))+(1-y_i)log(1-{\sigma }_W(x_i)))$$
极大似然估计计算部分参考https://zhuanlan.zhihu.com/p/138828549

1.3 求解

使用梯度下降法进行求解，用上述的$J(W)$对$W$求导，可得$W$的梯度及其下降方法：
$$\frac{\partial J}{\partial W}=\frac{1}{m}\sum _{i=1}^m({\sigma }_W(x_i)-y_i)x_i$$

$$W=W-lr\ast \frac{\partial J}{\partial W}$$
$lr$为学习率

二、代码实现

2.1 平面坐标点的分类

按照我们的想法，我们先简单在平面上构建几个点，并用逻辑斯蒂回归找出一条决策边界

import numpy as np
import matplotlib.pyplot as plt

#构建坐标点
X_True = [[7.0,3.2],[6.4,3.2],[6.9,3.1],[ 5.5,2.3 ],[6.5,2.8],[5.7,2.8]] 
X_False = [[5.1,3.5],[4.9,3.0 ],[4.7,3.2],[4.6,3.1],[5.0,3.6],[5.4,3.9 ]]
Y = [1] * len(X_True) + [0] * len(X_False)

X_All = X_True+X_False
X_All = np.array([[1]+x for x in X_All]) #这里在x中加入1，与b相乘

w = np.array([0,0,0]) #w中包含了b，第一个0为b
lr = 0.1 #学习率

def sigmoid(x):
    return 1/(1+np.exp(-x))

EPOCHS = 100
for epoch in range(EPOCHS):
    w = w - lr * np.mean((sigmoid(X_All.dot(w))-Y)*X_All.T,axis=1) #按照公式以矩阵形式进行处理

#得到w后可以画出决策边界
plot_x = np.arange(4,8)
plot_y = -(w[1]*plot_x + w[0])/w[2]

plt.scatter([x[0] for x in X_True] , [x[1] for x in X_True],c = 'r',label = '1')
plt.scatter([x[0] for x in X_False] , [x[1] for x in X_False],c = 'b',label = '0')
plt.plot(plot_x , plot_y , c = 'black')
plt.legend()
plt.show()

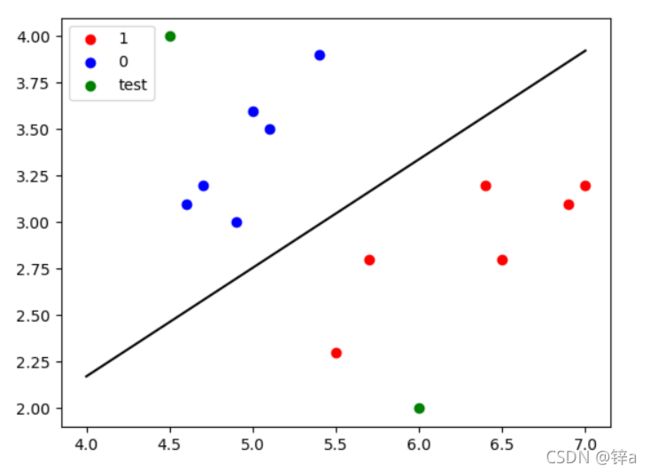
最终结果：

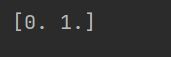
同时，我们还可以输入任意一组坐标点让模型去预测，如：

x_test = np.array([[1,4.5,4],[1,6.0,2]])  #注意，输入的坐标点第一个数为1，为了与b相乘。后面两位才是坐标值x和y。
logistic = sigmoid(x_test.dot(w))
logistic[logistic>=0.5] = 1
logistic[logistic<0.5] = 0
print(logistic)

在图中可以表示这两个点为：

预测结果：

正确地将坐标点分类

2.2 鸢尾花分类

鸢尾花数据集（iris）是最经典的机器学习开源数据集之一，它拥有4个特征：sepal length、 sepal width 、petal length、petal width ，我们将使用这4个特征通过逻辑斯蒂回归对其进行分类（由于这里做的是二分类，所以舍弃掉了第三类鸢尾花）

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

#获取数据
def get_data(): 
    data = load_iris().data
    label = load_iris().target
    df = pd.DataFrame(data)
    df.columns = [load_iris().feature_names]
    df['label'] = label

    df = df.loc[label != 2,:] #做二分类，舍弃掉第三类鸢尾花

    X = df[load_iris().feature_names]
    Y = df['label']

    return X.values,Y.values

#为了实现矩阵相乘所以将X添加第一个维度，置为1
def data_mat(x_origin):
    mat = []
    for d in x_origin:
        mat.append([1.0, *d])
    return np.array(mat)

#sigmoid函数
def sigmoid(x):
    return 1/(1+np.exp(-x))

#最后模型输出，其实也是sigmoid函数
def model(x,w):
    return 1 / (1 + np.exp(-x.dot(w)))

def predict(x_test,y_test,w):
	#两种计算方法
    #第一种wx > 0或者 <0
    y_predict = x_test.dot(w)
    y_predict[y_predict >= 0] = 1
    y_predict[y_predict < 0] = 0
	
    #第二种方法模型输出>= 0.5 或者 < 0.5
    # y_predict  = model(x_test,w)
    # y_predict[y_predict >= 0.5] = 1
    # y_predict[y_predict < 0.5] = 0
    
    return accuracy_score(y_test,y_predict)


if __name__ == '__main__':
    X,Y = get_data()
    x_train, x_test, y_train, y_test = train_test_split(X, Y, test_size=0.3) #将数据集划分为训练集和验证集

    x_train = data_mat(x_train) #矩阵化
    x_test = data_mat(x_test)

    EPOCHS = 100 #迭代次数
    W = np.array([0]*(x_train.shape[1])) #初试化W和b，注意b以及包含在w内，所以W的维度为特征数+1
    lr = 0.1 #学习率
    for epoch in range(EPOCHS): 
        #梯度下降学习参数
        W = W - lr * np.mean((sigmoid(x_train.dot(W)) - y_train.squeeze()) * x_train.T, axis=1)

    #对测试集进行测试
    result = predict(x_test,y_test,W)
    print('Predict_ACC：{}'.format(result))

最终结果：

预测准确率为1.0，完美地将鸢尾花进行了分类

三、联系方式

如有问题欢迎评论区指出，有问题也可以联系我：
[email protected]