用python写梯度下降算法实现逻辑斯蒂回归

1.logistic的理论基础

可参考网上一位大佬写的李航的《统计学习方法》笔记
pdf笔记文档链接：
链接：https://pan.baidu.com/s/1Gee9aOdNvemy5K6co1daZg
提取码：hlbb

具体算法步骤：

2.用python实现

数据使用iris数据集，iris数据集有三个类别，我们使用前两个类别作为因变量Y
iris数据集链接：
https://pan.baidu.com/s/17yA7n2so_EhxmXwn0RQXrQ
提取码：xboz

import numpy as np
import pandas as pd

# 1.加载数据；数据预处理
iris = pd.read_csv("iris.csv")
# iris数据集有三类， 这里将第三列删除，只使用第一类和第二类
iris = iris[~iris['Species'].isin(['virginica'])]
X = iris.iloc[:, 1:5]
Y = iris.iloc[:, 5]
# 将iris前两类的名称改为0和1
Y = Y.replace("setosa", 0)
Y = Y.replace("versicolor", 1)

# 将X转化成(x_1, x_2, ..., x_n, 1)的格式
X['one'] = 1
X = X.iloc[1:, :]
Y = Y.iloc[1:]
# 到这，数据预处理就完成了！

# 2.逻辑斯蒂回归算法
def g(w, X, Y):
    return np.sum(np.log(1 + np.exp(np.dot(X, w))) - np.multiply(np.dot(X, w), np.expand_dims(Y, axis=1)), axis=1)

class LOGISTIC(object):
    def __init__(self, X, Y, w=np.zeros(X.shape[1])):
        # w = (w1, w2, ..., wn, b)
        self.eta = 0.1
        self.epsilon = 0.001
        self.step = 0
        self.X = X
        self.w = w
        self.Y = Y

    def run(self):
        while True:
            P = np.exp(np.dot(self.X, self.w)) / (1 + np.exp(np.dot(self.X, self.w)))
            gradient_w = np.sum(np.multiply(self.X, np.expand_dims(P-self.Y, axis=1)), axis=0)
            gradient_w_norm = np.linalg.norm(gradient_w, ord=2)    # L2范数，等价于np.sqrt(np.sum(gradient_w**2))

            if gradient_w_norm < self.epsilon:
                return self.w, self.step
            else:
                w2 = self.w - self.eta*gradient_w
                if np.linalg.norm(g(w2, self.X, self.Y)-g(self.w, self.X, self.Y), ord=2) < self.epsilon or \
                        np.linalg.norm(w2-self.w, ord=2) < self.epsilon:
                    return self.w, self.step
                self.w = w2
            self.step += 1

# 测试
def test(w, x):
    p_0 = 1/(1+np.exp(np.dot(x, np.expand_dims(w, axis=1))))
    p_1 = 1 - p_0
    diff = p_0 - p_1
    diff[diff > 0] = 0
    diff[diff < 0] = 1
    return diff


log = LOGISTIC(X=X, Y=Y)
train_w, train_step = log.run()
# train_w即为训练得到的权重,train_step为训练的步数
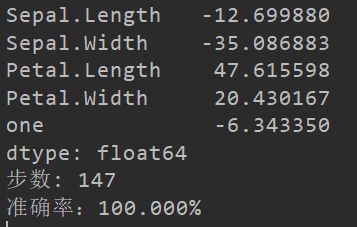
print(train_w)
print("步数:", train_step)

test_cls = test(train_w, X)
# test_cls即为logistic的判断结果
# print(test_cls)

# 计算准确率
acc = np.sum(test_cls - np.expand_dims(Y, axis=1) == 0)/test_cls.shape[0]
print("准确率：%.3f%%" % (acc*100))

运行结果：

注：代码是参照上面的算法步骤自己写的，如有问题，欢迎批评指正。