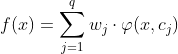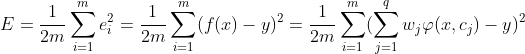机器学习算法——神经网络4（RBF神经网络）

RBF(Radial Basis Function,径向基函数)网络是一种单隐层前馈神经网络。它使用径向基函数作为隐层神经元激活函数，而输出层是对隐层神经元输出的线性组合。

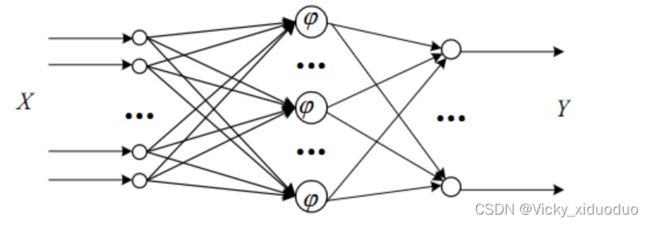
所以，RBF神经网络是一种三层神经网络，其包括输入层、隐层、输出层。从输入层到隐层的变换是非线性的，从隐层到输出层的变换是线性的。RBF神经网络结构如下图所示。

其中，我们称之为径向基函数，最常见的径向基函数是高斯径向基函数（或称为“高斯核函数”或者RBF核函数）。 高斯核函数定义如下：

其中，是第i个神经元的中心点，为高斯核的宽度。为样本点到中心点的欧式距离。

假定输入为d维向量x，输出为实值，则RBF网络可定义为：

其中，q为隐层神经元个数，wj是第j个隐层神经元所对应的权重，cj是第j个隐层神经元所对应的中心。

用均方误差定义误差函数，目标是为了最小化(累积)误差函数：

。

利用BP算法反向传播误差，并利用梯度下降法分别求得RBF网络参数，RBF需要的网络参数为 权重w,基函数的中心 c和高斯核宽度 。

输出层的神经元线性权重为：

隐层神经元中心点：

隐层的高斯核宽度：

对RBF不同的参数分别设置不同的学习率，经过多轮迭代直至误差函数收敛，结束训练。

RBF神经网络与BP神经网络的比较：

1. RBF的网络更加简单，一般是单隐层的网络；

2. RBF的输入项经过高斯转换映射到了高维空间，而BP网络就是输入项与权值之间的线性组合；

3. RBF网络的函数逼近能力和收敛速度一般要优于BP网络。

Python代码实现RBF网络：

先构建RBF网络，代码为：

import numpy as np
import matplotlib.pyplot as plt


class RBFNetwork(object):
    def __init__(self, hidden_nums, r_w, r_c, r_sigma):
        self.h = hidden_nums #隐含层神经元个数
        self.w = 0 #线性权值
        self.c = 0 #神经元中心点
        self.sigma = 0 #高斯核宽度
        #RBF一共要学习三个参数，w（权重）,c（基函数中心）,sigma（高斯核宽度）
        self.r = {"w": r_w
                  , "c": r_c
                  , "sigma": r_sigma
                  } #参数迭代的学习率,
        self.errList = [] #误差列表
        self.n_iters = 0 #实际迭代次数
        self.tol = 1.0e-5 #最大容忍误差
        self.X = 0 #训练集特征
        self.y = 0 #训练集结果
        self.n_samples = 0 #训练集样本数量
        self.n_features = 0 #训练集特征数量

    def init(self): #初始化参数
        sigma = np.random.random((self.h, 1))#(h,1) h隐藏神经元的个数（50，1）
        c = np.random.random((self.h, self.n_features))#(h,1) 基函数中心（50，1）
        w = np.random.random((self.h+1, 1))#(h+1,1)权重（51，1）

        return sigma, c, w

    #计算径向基距离函数
    def guass(self, sigma, X, ci):
        return np.exp(-np.linalg.norm((X-ci), axis=1)**2/(2*sigma**2))#按行向量处理

    #隐藏层输出数据
    def change(self, sigma, X, c):#sigma(50,1), X(500,1), c(50,1)
        newX = np.zeros((self.n_samples, len(c)))#newX(500,50)
        for i in range(len(c)):
            newX[:, i] = self.guass(sigma[i], X, c[i])
        return newX

    #输出层输入数据
    def addIntercept(self,X):   # X(500, 50),
        return np.hstack((X, np.ones((self.n_samples, 1))))#输出（500，51）

    #计算整体误差
    def calSSE(self, prey, y): #prey = yi_ouput
        return 0.5 * (np.linalg.norm(prey-y))**2

    #求l2范数的平方
    def l2(self, X, c):#c(50,1)
        m, n = np.shape(X) #m=50,n=1
        newX = np.zeros((m, len(c)))
        for i in range(len(c)):
            newX[:, i] = np.linalg.norm((X-c[i]), axis=1)**2
        return newX

    #训练
    def train(self, X, y, iters):
        self.n_samples, self.n_features = X.shape #样本量500个，特征1个
         #初始化参数
        sigma, c, w = self.init() #w(51,1) c(50,1)

        for i in range(iters):
            #正向计算过程
            hi_output = self.change(sigma, X, c)#隐层输出（500，50）

            yi_input = self.addIntercept(hi_output)#yi_input（500，51）输出层输入

            yi_output = np.dot(yi_input, w)#输出层输出 （500，51）与（51，1）点乘得（500，1）
            error = self.calSSE(yi_output, y)#计算误差
            if error < self.tol: #在误差内，直接可以跳出循环
                break
            self.errList.append(error)#否则，将误差存入列表中
            #误差反向传播过程
            deltaw = np.dot(yi_input.T, (yi_output-y)) #yi_input.T(51,500) · （500，1）=（51，1）
            w = w - self.r['w']*deltaw / self.n_samples #self.r['w']是学习率
            deltasigma = np.divide(np.multiply(np.dot(np.multiply(hi_output, self.l2(X, c)).T,
                                                      (yi_output-y)), w[:-1]), sigma**3)
            sigma -= self.r['sigma']*deltasigma/self.n_samples #self.r['sigma']是学习率
            deltac1 = np.divide(w[: -1], sigma**2)
            deltac2 = np.zeros((1, self.n_features))
            for j in range(self.n_samples): # n_samples:500
                deltac2 += (yi_output-y)[j] * np.dot(hi_output[j], X[j]-c)
            deltac = np.dot(deltac1, deltac2)
            c -= self.r['c']*deltac/self.n_samples
            self.n_iters = i
            if i % 100 == 0:
                print("第%s轮迭代得误差为：%s" %(i, error))
        self.c = c
        self.w = w
        self.sigma = sigma

预测函数为：

#预测
    def predict(self, X):
        hi_output = self.change(self.sigma, X, self.c)
        yi_input = self.addIntercept(hi_output)
        yi_output = np.dot(yi_input, self.w)
        return yi_output

主函数为：

if __name__ == "__main__":
    #hermit多项式为f(x) = 1.1(1-x+2x^2)exp(-x^2/2)
    X = np.linspace(-5, 5, 500)[:, np.newaxis] #等分找到500个样本点，然后np.newaxis增加一个维度
    y = np.multiply(1.1*(1-X+2*X**2),np.exp(-0.5*X**2))
    rbf =RBFNetwork(50, 0.1, 0.2, 0.1)#有50个隐层神经元，r_w=0.1, r_c=0.2, r_sigma=0.1
    rbf.train(X, y, 1000)
    fig, ax = plt.subplots(nrows=2)
    ax[0].plot(X, y, color = 'blue', linewidth = 2.0)
    hat_y = rbf.predict(X)
    ax[0].plot(X, rbf.predict(X), color = 'red', linewidth = 2.0)
    ax[1].plot(rbf.errList, color = 'blue', linewidth =2.0)
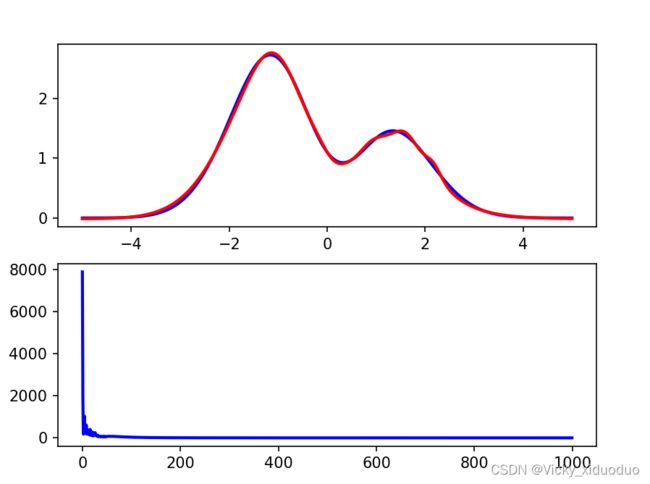
    plt.show()

上面设置的迭代次数为1000，输出的图像为(上面是看的与Hemit多项式拟合结果，图2显示的是携带次数与误差的结果)：

大家也可以设置不同的迭代次数，比如，设置成100，得到的图像为: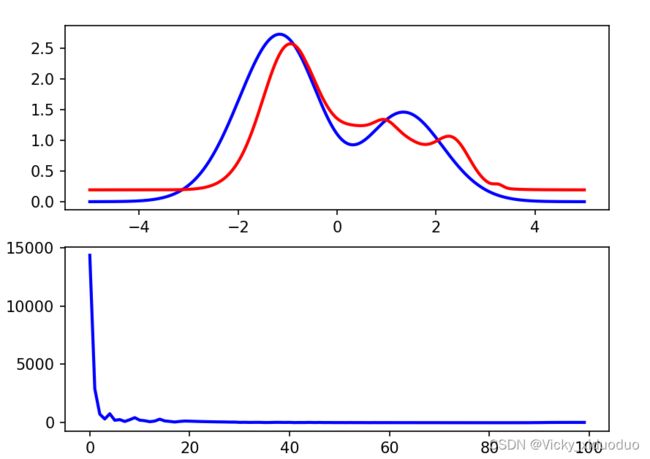 

 

 RBF网络讲解到此结束，欢迎大家留言讨论。