个性化推荐算法概述
本文为转载一思维导图内容，此链接为来源（完成本文时链接有效，不保证一直有效，如无效，望告知）
难点问题
1. 可扩展性：
能够保证在 user 和 item 数量持续增长时推荐算法的效果依然有效
2. 稀疏性：
如何解决 user 和 item 矩阵的稀疏性
3. 冷启动：
如何解决新用户上线、新物品上线的冷启动
4. 时效性：
新闻类内容需要考虑时效维度
5. 质量保证：
如何保证推荐的是高质量内容、内容消重
6. 动态性：
用户的兴趣是动态变化的
7. 多样性：
如何提高推荐内容的多样性
8. 准确性：
如何保证推荐内容符合目标用户的兴趣
9. 特征提取：
用户兴趣特征提取（建立用户兴趣标签）、内容特征提取
10. 推荐内容排序：
如何定义排序权重、同时要考虑避免过热以及增加冷门内容爆光
11. 正负反馈：
如何让用户做正负反馈并影响以后的推荐结果
推荐算法简介
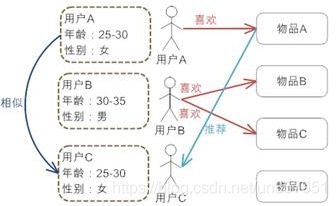
基于人口的统计学推荐（Demographic-based Recommendation）
原理：
是一种易于实现的推荐算法，它只是简单地根据系统用户的基本信息发现用户的相关程度，然后将相似用户喜爱的其他物品推荐给当前用户
优点：
- 因为不适用当前用户对物品的喜好历史数据，所以对于新用户来说，没有“冷启动（Cold Star）”的问题
- 这个方法不依赖物品本身的数据，所以这个方法在不同物品的领域都可以使用，它是领域独立的（domain-independent）
缺点：
- 这种基于用户的基本信息对用户进行分类的方法过于粗糙，尤其是对品味较高的领域，比如图书，电影和音乐等领域，无法得到很好的推荐效果
- 这个方法可能涉及到一些与信息发现问题本身无关却比较敏感的信息，比如用户的年龄等，这些用户信息不是很好获取
适用场景：
新用户只有基本信息，没有用户行为时，解决冷启动行为，，如首页的“浏览发现”
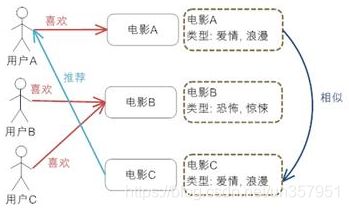
基于内容的推荐（Content-based Recommendation）
原理：
基于内容的关联性推荐，推荐用户喜欢和自己关注过的信息在内容上类似的信息；
例如，某人看了《三体1》，基于内容分的推荐算法会给其推荐《三体2》、《三体3》，算法认为这两者与其之前观看的内容上有非常大的关联性
优点：
- 推荐结果非常直观，内容之间有着非常高的关联性
- 可以极大地避免推荐的冷启动问题：如果某个新的信息内容上线，在没有被其他用户消费的情况下，其他几种推荐算法是不会推荐的；但是基于内容的推荐算法可以分析信息之间的关联信息，实现推荐
缺点：
- 由于推荐时仅根据内容的关联性做推荐，所以可能会对实时性或者说时间维度有缺陷
- 需要对物品进行分析建模，推荐的质量依赖于对物品模型的完整和全面程度
- 物品的相似性的分析仅仅依赖与物品本身的特性，这里没有考虑人对物品的态度
- 因为需要基于用户以往的喜好历史做出推荐，所以对与新用户有“冷启动”的问题
适用场景：
新用户有少量的用户行为时，发现更多相关的事物，多用于物品展示页中的“跟这个相似的物品有哪些”，适合电商网站中，引导用户查看更多同类的产品；常用关键词和标签（Tag）来描述物品元数据
适用领域：
电影、音乐、图书等的社交网站
基于协同过滤的推荐（collaborative Filtering-based Recommendation）
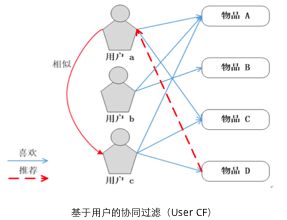
基于用户的协同过滤推荐（User-based Collaborative Filtering Recommendation, UserCF）
原理：
根据所有用户对物品或信息的偏好，发现与当前用户口味和偏好相似的“邻居”用户群
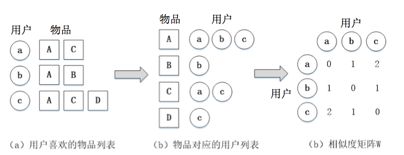
根据用户喜欢的物品列表得到物品对应的用户列表，从而计算用户相似度矩阵
常用算法：
K-近邻算法（K-neighborhood）
皮尔逊相关系数（Pearson correlation coefficient）
适用领域：
新闻类网站、小说、电影网站
适用场景：
适用于用户较少的场景，否则计算用户相似度矩阵代价很大
时效性较强，适用于用户个性化兴趣没有那么明显的领域
给用户推荐多样化的内容
场景举例：
豆瓣：“你可能感兴趣的电影”
今日头条：“为您推荐了 n 篇文章”
基于项目的协同过滤推荐（Item-based Collaborative Filtering Recommendation, ItemCF）
原理：
使用所有用户对物品或者信息的偏好，发现物品和物品之间的相似度，然后根据用户的历史偏好信息，将类似的物品推荐给用户
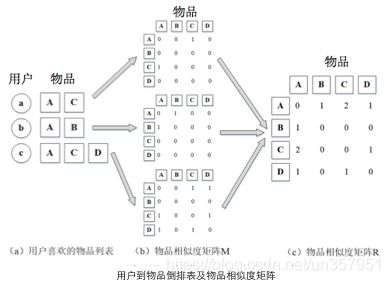
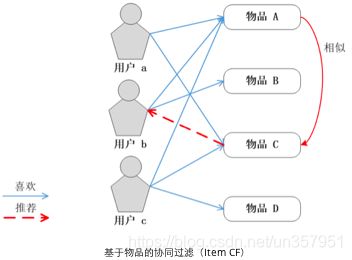根据用户喜欢的物品列表得到物品的相似度矩阵
常用算法：
基于物品相似度的推荐中，改进的余弦相似度效果更好
适用领域：
图书、电子商务、电影网站
适用场景：
物品数量明显小于用户数的场合，否则物品相似度矩阵代价太大
适合长尾物品丰富，用户个性化需求更强烈的领域
给用户推荐相似内容
场景举例：
起点：“喜欢这本书的人还喜欢”
亚马逊：“购买此商品的顾客也同时购买”
基于模型的协同过滤推荐（Model-based Collaborative Filtering Recommendation， ModelCF）
原理：
基于模型的协同过滤推荐就是基于样本的用户喜好信息，训练一个推荐模型，然后根据实时的用户喜好信息进行预测推荐
总结
优点：
- 基于其他用户行为集的推荐，都是相似行为的用户，可以保证个性化程度高
- 基于相同行为集的用户，容易让用户发现新的兴趣点
- 模型通用性强，不需要太多对应数据领域的专业知识
缺点：
- 由于该推荐算法必须要基于用户的历史行为，所以对新用户（没有历史行为的用户）推荐效果非常差
- 相同行为集的用户，用户喜好兴趣可扩展性很低
- 推荐质量完全基于历史行为，可能某个时间点消费国某类型的信息，后面又不喜欢了，后续系统还是会继续做推荐
- 无法基于场景进行推荐，难以根据用户所在的场景和用户当前的情绪进行推荐行为
- Scalability：由于其计算复杂度与用户或者物品的数量时超线性的关系，而且需要计算矩阵乘法，难以并行化，用来处理大规模问题比较困难
适用场景：
对于用户数量远远大于产品，并且产品相对稳定的电商系统，计算产品相似度计算量小，适用 ItemCF；反之，对于更新频繁，物品数量海量的新闻、博客、微博等系统，UserCF效果更好
基于规则的推荐算法
原理：
建立一套行为规则进行推荐，这类算法常见的比如基于用户点击、最多用户浏览等；常见的建立规则有：A推荐B，凡是看过A信息的用户给它推荐B信息
优点：
- 可以通过规则，让用户发现新的兴趣点
- 对于推荐算法，不需要了解太多的信息之间的关联知识，只需要根据规则进行推荐
缺点：
- 难以创建一套完善的推荐规则
- 该推荐完全是基于规则，导致个性化程度非常低，难以做到真正的个性化推荐
适用场景：
首页热榜；最多人浏览；最新内容；关注的人动态
计算相似性算法
K-近邻算法（K-neighborhood）
原理：
采用向量空间模型来分类，概念为相同类别的案例，彼此的相似度高，而可以借由计算与已知类别案例之相似度，来评估位置类别案例可能的分类
特点：
基于实例的学习方法，分类新的实例的开销可能很大
优点：
- 简单、易理解、易实现，无需估计参数、无需训练
- 适合对稀有事件进行分类
- 特别适合多分类问题（multi-model，对象具有多个类别标签），KNN比SVM的表现要好
缺点：
- 对训练集要求苛刻，KNN要求训练集不同类别的数据不能相差太多
- 计算量大，每一次都要计算未知数据和所有数据的距离
欧氏距离（Euclidean distance）
原理：
最常用的距离计算公式，衡量的是多维空间中各个点之间的绝对距离
表示相似度时，其值取距离加一的和的倒数——距离越小，相似度越大
特点：
- 非负性：距离是一个非负的数值
- 同一性：对象到自身的距离是0
- 对称性：距离是一个对称的函数
- 三角不等式：从对象 I 到对象 J 的直接距离不会大于途径任何对象 k 的距离
优点：
公式简单
缺点：
没有考虑分量之间的相关性，体现单一特征的多个分量会干扰结果
皮尔逊相关系数（Pearson correlation coefficient）
原理：
通过Pearson 相关系数来度量两个用户之间的相似性；计算时，首先找到两个用户共同评分过的项目集，然后计算这两个向量的相关系数；即相关分析中的相关系数 r，分别对 X 和 Y 基于自身总体标准化计算空间向量的余弦夹角；Pearson Correlation 实际上就是两个向量的余弦值，等于两个向量中心化后（减去均值）的内积除以长度的乘积
特点：
- 皮尔逊相关系数具有平移不变性和尺度不变性
- Pearson 考虑的是每个 Item 的被打分的均值
- 使用 Pearson 线性相关系数必须假定数据是成对地从正态分布中取得的，并且数据至少在逻辑范畴内必须是等间距的数据
优点：
可以避免评分等级膨胀的问题
缺点：
- 没有考虑用户之间重叠的评分项数量对相似度的影响
- 如果两个用户之间只有一个共同的评分项，相似度也不能被计算（计算过程中，被除数有 n-1）
- 如果重叠的值都相等，也无法计算相似性（标准差为0，做除数）
- Pearson 系数对绝对数值不敏感
余弦相似度（Cosin similarity）
原理：
把用户评分看做是 n 维项目空间上的向量，通过计算两个向量之间的夹角余弦来衡量两个用户之间的相似性
余弦相似度用向量空间中两个向量夹角的余弦值作为衡量两个个体之间差异的大小
相比距离度量，余弦相似度更加注重两个向量在方向上的差异，而非距离或者长度
特点：
余弦相似度受到向量的平移影响，如果将 x 平移到 x+1，余弦值就会改变
优点：
- 不受坐标轴旋转，放缩大小的影响
- 对系数数据也有比较好的结果
缺点：
余弦相似度对数值不敏感
调整余弦相似度（Adjusted cosin similarity）
原理：
将余弦相似度中的向量，减去用户平均评分向量后，再计算夹角余弦以修正不同用户评分尺度不同的问题
特点：
修正 cosin 考虑的是对 Item 打过分的每个 user 其打分的均值
优点：
修正余弦相似度对数值不敏感的问题
缺点：
增加了算法复杂度
如何选择相似性算法
- 如果数据存在 “分数膨胀” 问题，就使用皮尔逊相关系数
- 如果数据比较 “密集” ，变量之间基本都存在公有值，且这些距离数据非常重要，则选择欧氏距离或者曼哈顿距离
- 如果数据是稀疏的，则使用余弦相似度
- 调整余弦相似度和余弦相似度，皮尔逊相关系数在推荐系统中应用比较多；在基于项目的推荐中，已有论文证明，调整余弦相似度性能要优于后两者