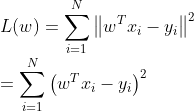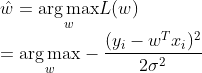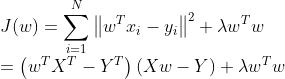机器学习——线性回归

目录

1、最小二乘法及其几何意义

2、最小二乘法-概率视角-高斯噪声-MLE(极大似然估计)

3、正则化-岭回归

4、正则化-岭回归-概率角度-高斯噪声高斯先验

---

这一阵子重新回顾了机器学习的几个基础模型和一些重要的概念。古人云：“温故而知新，可以为师矣”。且笔者自身在学习方面又有一些较大的问题，即当时沾沾自喜感觉自己学的挺快，掌握的也挺好，随之过几天重新思考同样问题的时候却又忘得一干二净，不得已又只能重新再看一遍。几番如此，学习进度踌躇不前，真是令人不堪其忧，所以特在此处总结几日所学和几夜所想，让自己彻彻底底的“慢”下来。师傅领进门，修行靠个人，废话不多说，正片开始。

假设有个样本点，其中

其中，。

具体拟合示意图如下所示：

图1. 线性回归拟合示例

1、最小二乘法及其几何意义

图1中红线代表拟合的直线：

现通过最小二乘估计计算与之间的预测误差：

将从连加形式写成矩阵形式，即：

其中为的转置，因此

,因为和均为一维实数，所以

，为了让达到最小值，即，现对求导

，即可得出

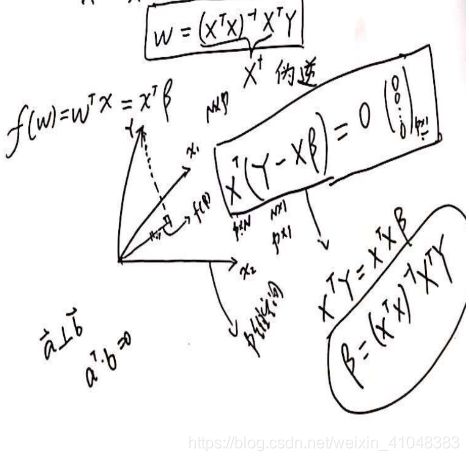
以上是将误差分散到每个样本点，现有误差函数的几何解释：

图2. 几何角度求出w的估计值

将，可看成在同一平面上的p维向量,Y为图2中所示方向，图2中虚线为，那么此时样本所在的平面垂直虚线，即：

上述表明可从两个角度求得，从几何角度来看是将误差分散在维向量上，从坐标轴中来看是将误差分散在各自的样本点上。

2、最小二乘法-概率视角-高斯噪声-MLE(极大似然估计)

假设数据的噪声服从高斯分布，，那么，所以有

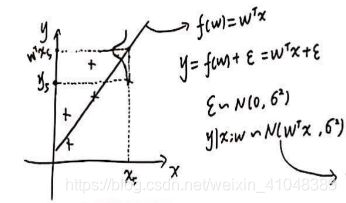
噪声服从高斯分布的图形化解释如下图所示：

图3. 噪声服从高斯分布的图形化解释

通过极大似然估计定义如下函数：

上式中与  无关，所以：

通过上式，即可在概率视角推出最小二乘公式。

3、正则化-岭回归

通过上文我们有损失函数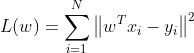：，并有，因为，如果存在远远大于，那么将在数学上解释为不可逆，在线性拟合方面上来讲容易造成过拟合，

为防止过拟合的发生，可以

• 加数据
• 特征选择/特征提取
• 正则化

正则化框架表示为：，后一项称之为惩罚项penalty。

针对线性回归，有两种正则化方案：

• 
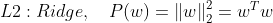•  ,L2也成为权值衰减。

加入  正则化的损失函数定义如下：

，因为、 和 均为一维实数，所以有：

，此时有 半正定矩阵 和 对角矩阵 一定正定，所以可逆。

为了让达到最小值，即，现对求导

，即可得出

从直观上来说，可以达到抑制过拟合的效果。

4、正则化-岭回归-概率角度-高斯噪声高斯先验

同第2节类似，噪声服从高斯分布，那么，所以有

从贝叶斯角度分析，为简化推导，令，所以有（注意与  的方差不同）

根据贝叶斯公式，我们有：，因为  与估计无关，所以可省略，即求  即可。

设想我们通过最大后验估计MAP来估计 ：

，因为加入函数对求  的没有影响，所以有：

，左式第一项与  无关，所以省略，得：

，第一项和第二项同乘以  ，因为存在负号，所以  取反得：

，加上 ，所以最终  得最大后验估计为：

，即有

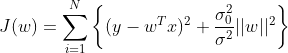，对比第3节得岭回归损失函数定义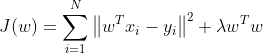：，可发现两式一致，均为惩罚项系数。

上述推导完美诠释了正则化从概率角度与本身定义之间的联系，也进一步表明了频率派与贝叶斯派之间的殊途同归。

为更加清楚的说明本文各小节之间的联系，现附上最小二乘估计和极大似然关系图：

图4. 最小二乘估计与极大似然估计

 

拟合示意图python代码：

#%%
import matplotlib


import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model
import pandas as pd

# Load CSV and columns
df = pd.read_csv("Housing.csv")

Y = df['price']
X = df['lotsize']

X=X.values.reshape(len(X),1)
Y=Y.values.reshape(len(Y),1)

# Split the data into training/testing sets
X_train = X[:-250]
X_test = X[-250:]

# Split the targets into training/testing sets
Y_train = Y[:-250]
Y_test = Y[-250:]

# Create linear regression object
regr = linear_model.LinearRegression()

# Train the model using the training sets
regr.fit(X_train, Y_train)

# Plot outputs
plt.scatter(X_test, Y_test,  color='black')
plt.title('Test Data')
plt.xlabel('Size')
plt.ylabel('Price')
plt.xticks(())
plt.yticks(())

# Plot outputs
plt.plot(X_test, regr.predict(X_test), color='red',linewidth=3)

plt.show()
#%%
# 画出训练集的拟合曲线，第一种方法predict
# Plot outputs
plt.scatter(X_train, Y_train,  color='black')
plt.title('Train Data')
plt.xlabel('Size')
plt.ylabel('Price')
plt.xticks(())
plt.yticks(())

# Plot outputs
plt.plot(X_train, regr.predict(X_train), color='red',linewidth=3)

plt.show()

#%%
# 画出训练集的拟合曲线，第二种方法coef_*x+intercept_ 
# Plot outputs
plt.scatter(X_train, Y_train,  color='black')
plt.title('Test Data')
plt.xlabel('Size')
plt.ylabel('Price')
plt.xticks(())
plt.yticks(())

# Plot outputs
plt.plot(X_train, regr.coef_*X_train+regr.intercept_, color='red',linewidth=3)

plt.show()

#%%
# 查看coef_*x+intercept_的值和regr.predict()的值是否相等，相减为0
regr.coef_*X_train+regr.intercept_ - regr.predict(X_train)

代码涉及数据集下载链接：https://vincentarelbundock.github.io/Rdatasets/csv/Ecdat/Housing.csv

参考资料：

1. 机器学习-白板手推系列
2. python tutorials: Linear Regression