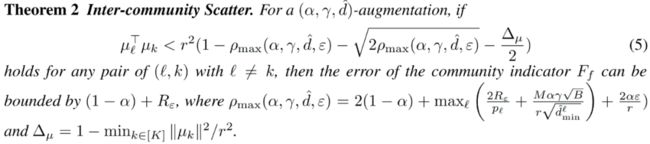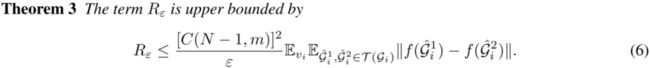NeurIPS 2022｜图对比学习的结构公平性初探

©作者 | 王睿嘉

单位 | 北邮 GAMMA Lab

研究方向 | 图神经网络

论文标题：

Uncovering the Structural Fairness in Graph Contrastive Learning

收录会议：

NeurIPS 2022

论文链接：

https://arxiv.org/abs/2210.03011

节点表示学习对结构公平性有所要求，即在度小和度大节点上都有良好的性能表现。最近研究表明，图卷积网络 (GCN) 常对度小节点的预测性能较差，在广泛存在的度呈长尾分布的图上表现出结构不公平。图对比学习 (GCL) 继承了 GCN 和对比学习的优势，甚至在许多任务上超越了半监督 GCN。那么 GCL 针对节点度的表现又如何呢？是否可能为缓解结构不公平提供新的思路？

背景

最近研究表明[1]，图神经网络（GCN）表现出结构不公平，即对度大节点（头节点）的预测性能较佳，而度小节点（尾节点）较差。由于实际场景中的节点度通常遵循长尾幂律分布，GCN 的这种结构不公平会导致一定的性能瓶颈。

图对比学习（GCL）取 GCN 和对比学习之长处，使节点表示学习不依赖监督信息的同时，在一些任务上的性能比肩甚至超越半监督 GCN。现有 GCL 方法一般对输入随机增广，并设置合适的正负例来对比优化 GCN 编码器。由此，不禁好奇：GCL 是否会继承 GCN 的结构不公平性？

我们通过实验探究，惊奇地发现 GCL 方法中度大和度小节点间的性能差距小于 GCN，展现出缓解结构不公平性的潜力。此时，一个关键的问题自然出现：为什么 GCL 对度偏差更公平？

该问题的答案可以为缓解结构不公平性提供新的思路，并加深我们对 GCL 机制的理解。

直观地，图增广使尾节点有机会产生更多的社区内边，与同社区节点的表示更近，从而远离社区边界，易于分类。理论地，我们通过证明社区内集中定理和社区间分散定理揭示 GCL 所得节点表示呈现清晰的社区结构。这些定理与 GCL 的两个核心部分相关：正例的对齐，恰为 GCL 的优化目标；预定义的图增广策略，影响增广表示的集中程度。

由此，我们我们建立了图增广与表示集中间的关系，并提出基于新的图增广策略的 GCL 模型（GRADE）来进一步提升结构公平性。具体地，GRADE 将尾节点和相似节点的自我中心网络插值，使尾节点邻域包含更多相同社区的节点；将头节点的自我中心网络提纯以减弱不同社区节点带来的噪音。在多种基准数据集和评估协议下的实验充分验证了 GRADE 的有效性。

GCL结构公平性的实验探究

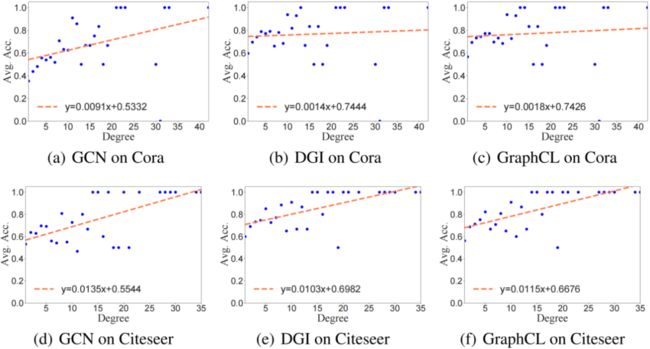
选取两个具有代表性的 GCL 模型 DGI[2] 和 GraphCL[3]，分析其结构公平性。具体地，我们将GCN、DGI 和 GraphCL 分别在 Cora、Citeseer、Photo 和 Computer 数据集上训练，并根据度将节点分组，计算这些组的平均准确率，如图所示。

为进一步反映结构公平性，我们用线性回归拟合这些散点，斜率越小，该模型对度偏差越公平。Photo 和 Computer 数据集上的实验结果，参见论文。从图中可以看出，DGI 和 GraphCL 尾节点的平均准确率高于 GCN，且回归线的斜率也较小。这一有趣的现象说明，无监督的 GCL 方法比半监督的 GCN 更具有结构公平性。

GCL结构公平性的理论分析

图定义为 ，其中 是 个节点组成的节点集 ， 是边集， 是节点特征矩阵， 代表节点 的特征。边集可以用邻接矩阵 表示，如果 ，则 。给定无标签的训练集，每个节点属于 个社区 之一。假设增广集 包含所有可能的拓扑增广策略，节点 的自我中心网络 可能产生的所有正例集为 。

GCL 的目标是学到合理的 GCN 编码器 使得正例对间相近，而负例对间相远。这里，我们聚焦于拓扑增广和单层 GCN：

其中 是转移矩阵 的第 行， 是加自环的邻接矩阵， 是度矩阵。我们使用社区指示器 

其中 是社区中心， 代表 范数。社区指示器 的误差形式化为：

基于以上定义，记正例对表示间距离不大于 的节点集为 。

假设非线性变换具有 -Lipschitz 连续性，即 ，拓扑增广均匀采样 条边 ，且存在半径 使任意增广都有 。可证：

该定理建立了表示的社区内集中程度与 中正例对对齐程度间的关系。具体地，社区内集中需要较小的 。对比学习优化框架正是缩小正例对间的距离，因而 GCL 满足要求。

接下来，我们证明 GCL 还具有社区间分散的特性。对于增广集 ，将两节点间的增广距离定义为其变换前表示的最小距离，

其中 是增广后的邻接矩阵 的第 行， 为增广后的度。基于增广距离，我们引入 -augmentation 的定义用于衡量变换前表示的集中程度。

越大的 和越小的 说明变换前表示越集中。假设表示被归一化 ，且 。我们同时约束社区间距离和社区指示器误差：

为更准确地分配社区，不等式右边应接近 ，因而需要 较小。我们进一步通过对比框架中的正例对对齐损失约束 ：

所有定理证明参见原文。综上，社区间距离和社区指示器的误差由两个因素主导：1）正例对的对齐，较好的对齐可使 较小，从而 较小；2）增广表示的集中程度，更集中则 更大。

小的 和大的 会直接减小社区指示器的误差，并为社区间分散提供小的 。需要强调的是，第一个因素是 GCL 的对比目标，反映 GCL 结构公平的原因。而第二个因素取决于图增广策略的设计。在此驱动下，我们提出可以进一步集中增广表示的图增广方式。

GRADE

图增广

我们通过同时扰动原始特征和拓扑生成两个增广 和 ，并将两增广所得节点表示记为 和 。

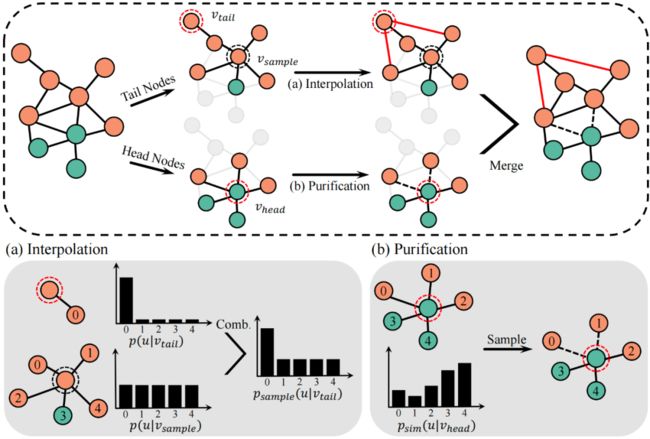
为获得更集中的增广表示，需要增加社区内边，减少社区间边。由于尾节点和头节点的结构属性不同，我们分别设计了不同的拓扑增广策略，如图所示。为扩展尾节点邻域以包含更多相同社区的节点，我们将锚尾节点 与采样所得相似节点 的自我中心网络插值。为防止增广过程注入许多不同社区节点，进一步依据 和 间的相似性调整插值比率。对于头节点，我们则利用相似性采样来提纯其邻域，尽量移除社区间边。

形式化地，我们基于节点表示间的余弦相似度构建相似度矩阵 ，对 有 ，否则 。对于任意尾节点 ，自多峰分布 中采样出节点 ，其中 是 中对应于节点 的行向量。

然后，将 和 的邻居分布插值，为尾节点 创建新的相似度感知邻域。这里，节点 的邻居分布定义为 ，如果 ，否则 。为减少不同社区节点带来的噪音，相似度 用作插值比率 ，

然后，从邻居分布 中进行不替换采样。对任意头节点 ，定义用于提纯的相似性分布。具体地，如果 ，则节点 的相似性分布为 ，否则 。基于相似性分布 ，不替换地采样出 个邻居，其中 是边丢弃率。通过这种相似性采样，不同社区间的边往往会被移除，从而保留有效的邻域信息。

至于特征增广，我们随机产生掩码向量 来隐去节点特征中的部分维度。掩码 中的每个元素都是从贝努利分布 中采样所得，其中超参数 是特征丢弃率。因此，增广后的特征 为：

在实现时，设置阈值 区分尾节点和头节点。增广 和 应用相同的超参数 和 。

优化目标

对节点 ，不同图增广得到的节点表示 和 构成正例对，而其他节点的表示被视为负例。因此，每个正例对 的目标函数定义为：

其中 是温度系数， 是 ， 是多层感知器（MLP），用于增强表达能力[4]。因此，总体目标函数是最大化所有正例对的平均值：

实验

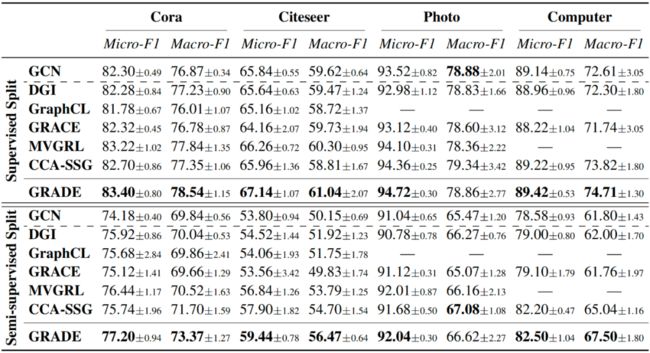
我们将 GRADE 与最具代表性的 GCL 模型 DGI、GraphCL、GRACE、MVGRL 和 CCA-SSG 进行比较，并同时评估半监督 GCN 以供参考。对于 GCL 模型，每个模型以无监督方式进行训练后，所得节点表示喂入逻辑回归分类器，并采用常见的两种划分方式进行评估：1）半监督划分，每类 20 个标记节点用于训练，1000 个节点用于测试；2）监督划分，1000 个节点用于测试，其余节点用于训练。GCN 同样遵循上述划分进行训练。

节点分类

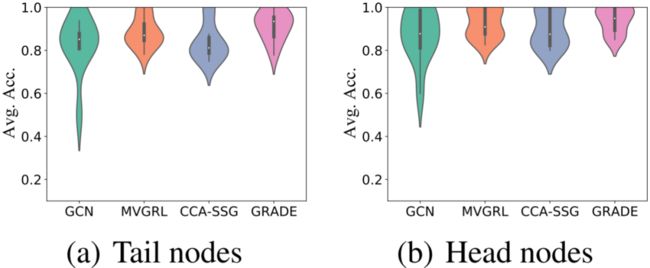
10 次独立实验的平均值和标准差如上表所示。在大多数情况下，GRADE 优于所有基线方法。GRADE 在 Cora 和 Citeser 数据集上的提升更显著，因为这两个数据集的平均节点度约为 3，存在大量尾节点。为验证 GRADE 在提高尾节点分类性能的同时保留了头节点的性能，我们根据阈值 将 Cora 的测试节点分为尾节点和头节点，并在小提琴图中绘制其平均准确率。正如预期，无论尾节点还是头节点，GRADE 都有较明显的性能提升。

公平性分析

为定量分析结构公平性，定义组平均为所有以度分组的平均准确度的平均值，而偏差定义为方差。

基于这些指标，评估结果如下表所示。可以看出，GRADE 降低了所有数据集的偏差，并保持最高的组平均。

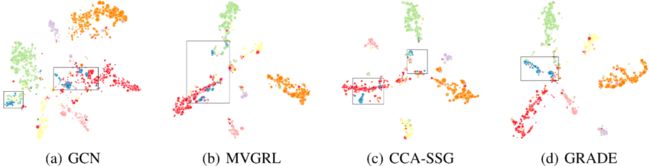
可视化

为证明 GRADE 使社区更集中，我们可视化了 Cora 数据集上 GRADE 和基线的节点表示。以蓝色社区为例，图对比学习基线虽比 GCN 有更清晰的社区边界，但蓝色节点仍很分散。在 GRADE 中，它们聚集在一起，说明增广策略发挥了重要作用。

更多实验，请参考原文。

参考文献

[1] Jian Kang, Yan Zhu, Yinglong Xia, Jiebo Luo, and Hanghang Tong Rawlsgcn: Towards rawlsian difference principle on graph convolutional network. In WWW, 2022. 

[2] Petar Velickovic, William Fedus, William L Hamilton, Pietro Liò, Yoshua Bengio, and R Devon Hjelm. Deep graph infomax. In ICLR, 2019. 

[3] Yuning You, Tianlong Chen, Yongduo Sui, Ting Chen, Zhangyang Wang, and Yang Shen. Graph contrastive learning with augmentations. In NeurIPS, 2020. 

[4] Ting Chen, Simon Kornblith, Mohammad Norouzi, and Geoffrey E. Hinton. A simple framework for contrastive learning of visual representations. In ICML, 2020.