Datawhale 零基础入门数据挖掘-Task2 数据分析
Datawhale 零基础入门数据挖掘-Task 2 数据分析
赛题:心电图心跳信号多分类预测
2.1 EDA 目标
- EDA的价值主要在于熟悉数据集,了解数据集,对数据集进行验证来确定所获得数据集可以用于接下来的机器学习或者深度学习使用。
- 当了解了数据集之后我们下一步就是要去了解变量间的相互关系以及变量与预测值之间的存在关系。
- 引导数据科学从业者进行数据处理以及特征工程的步骤,使数据集的结构和特征集让接下来的预测问题更加可靠。
- 完成对于数据的探索性分析,并对于数据进行一些图表或者文字总结并打卡。
2.2 内容介绍
- 载入各种数据科学以及可视化库:
- 数据科学库 pandas、numpy、scipy;
- 可视化库 matplotlib、seabon;
- 载入数据:
- 载入训练集和测试集;
- 简略观察数据(head()+shape);
- 数据总览:
- 通过describe()来熟悉数据的相关统计量
- 通过info()来熟悉数据类型
- 判断数据缺失和异常
- 查看每列的存在nan情况
- 异常值检测
- 了解预测值的分布
- 总体分布概况
- 查看skewness and kurtosis
- 查看预测值的具体频数
2.3 代码示例
2.3.1 载入各种数据科学与可视化库
#coding:utf-8
#导入warnings包,利用过滤器来实现忽略警告语句。
import warnings
warnings.filterwarnings('ignore')
import missingno as msno
import pandas as pd
from pandas import DataFrame
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
2.3.2 载入训练集和测试集
导入训练集train.csv
import pandas as pd
from pandas import DataFrame, Series
import matplotlib.pyplot as plt
Train_data = pd.read_csv('./train.csv')
导入测试集testA.csv
import pandas as pd
from pandas import DataFrame, Series
import matplotlib.pyplot as plt
Test_data = pd.read_csv('./testA.csv')
所有特征集均脱敏处理(方便大家观看)
- id - 心跳信号分配的唯一标识
- heartbeat_signals - 心跳信号序列
- label - 心跳信号类别(0、1、2、3)
data.head().append(data.tail())——观察首尾数据
data.shape——观察数据集的行列信息
观察train首尾数据
Train_data.head().append(Train_data.tail())
观察train数据集的行列信息
Train_data.shape
(100000, 3)
观察testA首尾数据
Test_data.head().append(Test_data.tail())
id heartbeat_signals
0 100000 0.9915713654170097,1.0,0.6318163407681274,0.13...
1 100001 0.6075533139615096,0.5417083883163654,0.340694...
2 100002 0.9752726292239277,0.6710965234906665,0.686758...
3 100003 0.9956348033996116,0.9170249621481004,0.521096...
4 100004 1.0,0.8879490481178918,0.745564725322326,0.531...
19995 119995 1.0,0.8330283177934747,0.6340472606311671,0.63...
19996 119996 1.0,0.8259705825857048,0.4521053488322387,0.08...
19997 119997 0.951744840752379,0.9162611283848351,0.6675251...
19998 119998 0.9276692903808186,0.6771898159607004,0.242906...
19999 119999 0.6653212231837624,0.527064114047737,0.5166625...
观察testA数据集的行列信
Test_data.shape
(20000, 2)
2.3.3 总览数据概况
- describe种有每列的统计量,个数count、平均值mean、方差std、最小值min、中位数25% 50% 75% 、以及最大值 看这个信息主要是瞬间掌握数据的大概的范围以及每个值的异常值的判断,比如有的时候会发现999 9999 -1 等值这些其实都是nan的另外一种表达方式,有的时候需要注意下
- info 通过info来了解数据每列的type,有助于了解是否存在除了nan以外的特殊符号异常
data.describe()——获取数据的相关统计量
data.info()——获取数据类型
获取train数据的相关统计量
Train_data.describe()
id label
count 100000.000000 100000.000000
mean 49999.500000 0.856960
std 28867.657797 1.217084
min 0.000000 0.000000
25% 24999.750000 0.000000
50% 49999.500000 0.000000
75% 74999.250000 2.000000
max 99999.000000 3.000000
获取train数据类型
Train_data.info
获取testA数据的相关统计量
Test_data.describe()
id
count 20000.000000
mean 109999.500000
std 5773.647028
min 100000.000000
25% 104999.750000
50% 109999.500000
75% 114999.250000
max 119999.000000
获取testA数据类型
Test_data.info()
RangeIndex: 20000 entries, 0 to 19999
Data columns (total 2 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 id 20000 non-null int64
1 heartbeat_signals 20000 non-null object
dtypes: int64(1), object(1)
memory usage: 312.6+ KB
2.3.4 判断数据缺失和异常
data.isnull().sum()——查看每列的存在nan情况
查看trian每列的存在nan情况
Train_data.isnull().sum()
id 0
heartbeat_signals 0
label 0
dtype: int64
查看testA每列的存在nan情况
Test_data.isnull().sum()
id 0
heartbeat_signals 0
dtype: int64
2.3.5 了解预测值的分布
Train_data['label']
0 0.0
1 0.0
2 4.0
3 0.0
4 0.0
...
99995 4.0
99996 0.0
99997 0.0
99998 0.0
99999 1.0
Name: label, Length: 100000, dtype: float64
Train_data['label'].value_counts()
0.0 58883
4.0 19660
2.0 12994
1.0 6522
3.0 1941
Name: label, dtype: int64
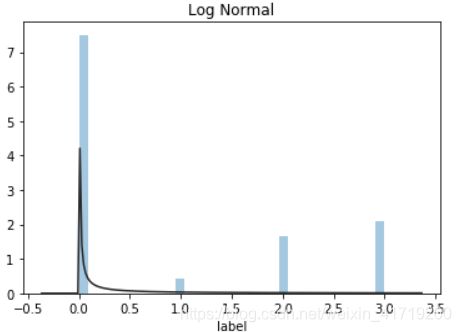
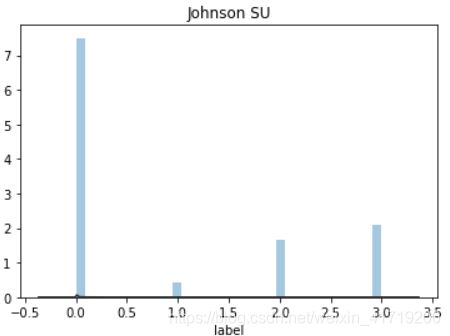
## 1) 总体分布概况(无界约翰逊分布等)
y = Train_data['label']
plt.figure(1); plt.title('Default')
sns.distplot(y, rug=True, bins=20)
plt.figure(2); plt.title('Normal')
sns.distplot(y, kde=False, fit=st.norm)
plt.figure(3); plt.title('Log Normal')
sns.distplot(y, kde=False, fit=st.lognorm)
plt.figure(4); plt.title('Johnson SU')
sns.distplot(y, kde=False, fit=st.johnsonsu)
上图我们可以看出lebal不服从正态分布,所以在进行回归之前,必须进行转换。上图可知,对数变换表现更好。
偏度和峰度(skewness and kurtosis) :
偏度(skewness),是统计数据分布偏斜方向和程度的度量,是统计数据分布非对称程度的数字特征。定义上偏度是样本的三阶标准化矩。偏度定义中包括正态分布(偏度=0),右偏分布(也叫正偏分布,其偏度>0),左偏分布(也叫负偏分布,其偏度<0)。
峰度(peakedness;kurtosis)又称峰态系数。表征概率密度分布曲线在平均值处峰值高低的特征数。直观看来,峰度反映了峰部的尖度。随机变量的峰度计算方法为:随机变量的四阶中心矩与方差平方的比值。峰度包括正态分布(峰度值=3),厚尾(峰度值>3),瘦尾(峰度值<3)。
# 2)查看skewness and kurtosis
sns.distplot(Train_data['label']);
print("Skewness: %f" % Train_data['label'].skew())
print("Kurtosis: %f" % Train_data['label'].kurt())
Skewness: 0.871005
Kurtosis: -1.009573
Train_data.skew(), Train_data.kurt()
(id 0.000000
label 0.871005
dtype: float64, id -1.200000
label -1.009573
dtype: float64)
sns.distplot(Train_data.kurt(),color='orange',axlabel ='Kurtness')
## 3) 查看预测值的具体频数
plt.hist(Train_data['label'], orientation = 'vertical',histtype = 'bar', color ='red')
plt.show()
2.4 个人收获
我没有做过时间序列分析的这种,所以还是用寻常价格的思路来做EDA,发现区别还是挺大的,优先用无界约翰逊分布处理发现效果反而没有对数正态分布的效果理想;偏度为0.8,大于0,说明label为正偏态,极端值分布在右侧;峰度为-1.0,小于3,说明曲线比较平滑;baseline中的label是有4.0这种异常值的,而现有数据集中未见这种异常值,所以未作处理。