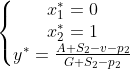演化博弈及Python实现
目录
一、写在前面
二、演化博弈
三、模型构建
3.1博弈收益矩阵
3.2综合期望
3.3复制动态方程
3.4可能的均衡点
3.5局部稳定分析法
四、理论分析
4.1演化相位图
4.2偏导
五、代码实现
5.1导入库
5.2设置复制动态方程及微分计算
5.3绘图
5.4效果
六、鞍点E坐标变化对演化博弈的影响
零、效果
一、写在前面
参考资料：
①：区块链下的仓单质押银企演化博弈分析
②：基于服务化的制造企业与服务提供商的演化博弈分析
③：基于演化博弈的区块链技术在供应链金融中的应用研究
本文主要以参考资料1为基础进行介绍与说明！
二、演化博弈
不同于传统的经典博弈论，演化博弈理论是把博弈理论分析和动态演化过程分析结合起来的一种理论，其强调的是一种动态理论。Maynard Smith和Price将生物进化理论引入到博弈论提出演化博弈论，在演化博弈论中的纳什均衡是参与方根据各自所面对的环境不断调整决策最终实现均衡的动态过程。
在传统博弈理论中，常常假定参与人是完全理性的，且参与人在完全信息条件下进行的，但在现实的经济生活中的参与人来讲，参与人的完全理性与完全信息的条件是很难实现的。在企业的合作竞争中，参与人之间是有差别的，经济环境与博弈问题本身的复杂性所导致的信息不完全和参与人的有限理性问题是显而易见的。
完全理性对博弈主体的理性要求十分严格，因为理性程度高可以使得博弈数学分析更加方便可靠。然而实际生活中的决策环境十分复杂，信息存在着不对称等现象，博弈方很难掌握所有的信息并进行完全理性的思考，因此有限理性才是比较实际的做法。很显然有限理性博弈需要考虑的因素更多，它比完全理性博弈更加复杂，而演化博弈就是一种有限理性的博弈方法，复制动态和演化稳定策略则是演化博弈的核心。
三、模型构建
①根据静态博弈得出博弈收益矩阵->②计算不同决策期望收益及综合期望->③求出复制动态方程->④可能的均衡解->⑤采用雅可比矩阵的局部稳定分析法对均衡点进行判断->⑥演化相位图等
本文以已公开发布的参考资料①为基础进行复现！
3.1博弈收益矩阵
根据自己的博弈主体与各博弈主体在不同策略下得到的收益可以得到博弈支付矩阵！
参考资料：博弈论->静态博弈
3.2综合期望
在得出博弈收益矩阵后，可以计算各个博弈主体在不同决策时的期望收益，最后计算综合期望收益
以上述博弈收益矩阵中的中小企业为例：
①当中小企业选择还款策略时（概率x），银行有y的概率要求上链，有1-y的概率要求上链，于是可以得到还款策略的期望收益为Ex=y[S1+G+(a-θ)Q1+K1+Q2+v-C]+(1-y)(S1+Sm+v-p1)。
②当中小企业选择不还款策略时（概率1-x），同上，即把银行的概率乘上相应策略组合下中小企业的收益即可。
③综合期望收益
同理，可以求得银行相应策略下的期望收益及综合期望收益
3.3复制动态方程
以中小企业为例，复制动态方程为：
![F(x)=\frac{dx}{dt}=x(E_x-\overline{E_x})=x(E_x-xE_x-(1-x)E_{1-x}) \\=x(1-x)(E_x-E_{1-x})=x(1-x)[y(G-p_2+S_2)+v+p_2-A-S_2]](http://img.e-com-net.com/image/info8/1070094c349443078db81cd00effacde.gif)
同理，可以计算得到银行的复制动态方程为：
![F(y)=\frac{dy}{dt}=y(E_y-\overline{E_y})=y(E_y-yE_y-(1-y)E_{1-y}) =y(1-y)(E_y-E_{1-y})\\=y(1-y)[x(p_2-p)+p-C+(a-\theta )Q_2+K_2Q_1-p_1-p_2+c_1+R_m]](http://img.e-com-net.com/image/info8/37eea9594998462fadcdc52920af2f24.gif)
总之，复制动态方程主要以下这一形式：
3.4可能的均衡点
在求得各博弈主体的复制动态方程后，分别令该方程为0，就可以得到可能的均衡解：
对于中小企业：
令F(x)=dx/dt=0，即可得到三个可能的均衡解：
对于银行：
令F(y)=dy/dt=0，即可得到三个可能的均衡解：
于是，可能的稳定平衡点有（0,0）、(1,1)、(0,1)、(1,0)与{（x*,y*)|x*与y*∈(0,1)}
3.5局部稳定分析法
分别对中小企业与银行的复制动态方程求关于x与y的偏导数，得到雅可比矩阵为：
雅可比矩阵的局部稳定分析法，若矩阵行列式大于0，迹小于0，即表示点为稳定点ESS
detJ=a11a22-a12a21>0
trJ=a11+a22<0
以点(1,1)为例，可以计算得到det J>0，tr J<0，因此点(1,1)为稳定点ESS(volutionarily stable strategy)。
此处不赘述，具体参考参考资料①， 该文献里对鞍点（x*,y*)的正负进行分类讨论，然后依次采用局部稳定分析法进行判别。该步骤可以根据自己实际推导出的模型进行判断，如果鞍点的正负容易判断的话，则不需要此步骤。
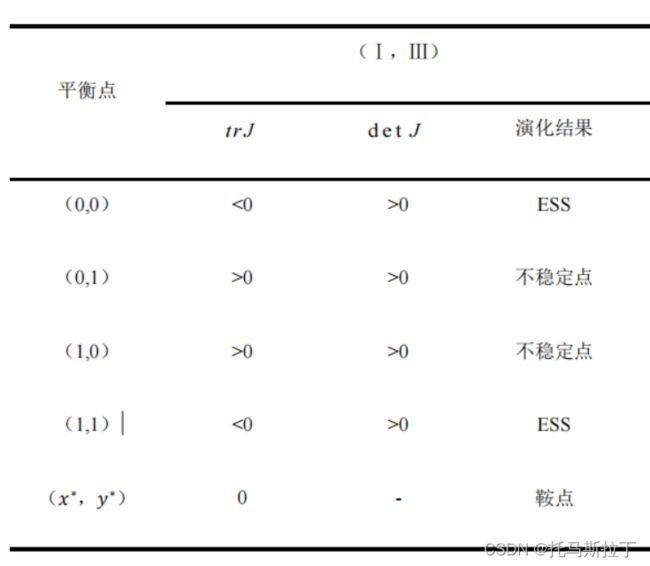
均衡点稳定性分析结果如下：
从上表可以看出(0,0)与(1,1)为演化平衡点，即（还款、要求上链）与（不还款、不要求上链）为最终的演化稳定策略。
四、理论分析
4.1演化相位图
根据上述稳定性分析结果，可得演化相位图如下：
4.2偏导
从演化相位图可以看出，当博弈双方的决策落在右侧四边形AECB时，演化博弈会向(1,1)点演化；反之，当当博弈双方的决策落在左侧四边形OAEC时，演化博弈会向(0,0)点演化。
于是，系统演化的概率可以用两块区域面积的大小来表示，而两侧四边形面积的大小取决于鞍点E。从图可以明显看出，随着鞍点E的横纵坐标减小，右侧四边形AECB的边际越大，中小企业还款与银行要求上链的概率就越大。
因此，有必要分析四边形AECB面积大小随各参数的变化。
从演化相位图易得，四边形AECB的面积为：
![S_{AECB}=\frac{1}{2}[(1-x^*)+(1-y^*)]](http://img.e-com-net.com/image/info8/d4744facf87d4f02982a771b93d4d8cc.gif){kind=small}
此处以p为例，早保证其他参数不变的情况下，对SAECB关于p求偏导，得到以下结果：
于是从偏导可以看出，随着p的增大，四边形AECB的面积增大。说明上链之后中小企业随着惩罚的加大，守约的概率越大，银行会继续选择上链的方式来监管中小企业的还款行为。
其余参数亦同，即通过求导分析各参数取值的变化为四边形AECB的影响！
五、代码实现
5.1导入库
import random
import matplotlib.pyplot as plt
from pylab import *
plt.rcParams['axes.unicode_minus']=False #用于解决不能显示负号的问题
mpl.rcParams['font.sans-serif'] = ['SimHei']5.2设置复制动态方程及微分计算
为简化代码，此处复制动态方程为随手写的鞍点坐标为(0.5,0.5)！
此处应根据自己所构建的模型的复制动态方程进行相应的修改！！！
#各博弈主体动态复制方程
def f(x,y):
return x*(1-x)*(5*y-2.5)
def g(x,y):
return y*(1-y)*(4*x-2)
#initX-x初始值
#initY-y初始值
#dt-步长
#epoch-迭代次数
def calculateValue(initX, initY, dt, epoch):
x = []
y = []
#演化初始赋值
x.append(initX)
y.append(initY)
#微量计算及append
for index in range(epoch):
tempx = x[-1] + (f(x[-1],y[-1])) * dt
tempy = y[-1] + (g(x[-1],y[-1])) * dt
x.append(tempx)
y.append(tempy)
return (x, y)5.3绘图
plt.figure(figsize=(7,7))
D=[]
#随机生成200个初始点
for index in range(200):
random_a=random.random()
random_b=random.random()
#步长dt为0.001 迭代次数1000
d=calculateValue(random_a,random_b,0.001,1000)
D.append(d)
for n,m in D:
plt.plot(n,m)
plt.ylabel("$y$",fontsize=25)
plt.xlabel("$x$",fontsize=25)
plt.tick_params(labelsize=25)
plt.xticks([0,0.2,0.4,0.6,0.8,1])
plt.grid(linestyle=":",color="b",linewidth=1)
plt.savefig("test",dpi=300,bbox_inches ="tight")
5.4效果
六、鞍点E坐标变化对演化博弈的影响
第五节的示例的微分方程中，可以轻易算出鞍点坐标为(0.5,0.5)
因此，本节首先对复制动态方程稍作修改，并绘出不同鞍点坐标情况下的演化博弈图进行对比！
代码如下：
import matplotlib.pyplot as plt
from pylab import *
plt.rcParams['axes.unicode_minus']=False #用于解决不能显示负号的问题
mpl.rcParams['font.sans-serif'] = ['SimHei']
import random
#各博弈主体动态复制方程
def f(x,y):
return x*(1-x)*(5*y+Z-2.5)
def g(x,y):
return y*(1-y)*(4*x+Z-2)
#initX-x初始值
#initY-y初始值
#dt-步长
#epoch-迭代次数
def calculateValue(initX, initY, dt, epoch):
x = []
y = []
#演化初始赋值
x.append(initX)
y.append(initY)
#微量计算及append
for index in range(epoch):
tempx = x[-1] + (f(x[-1],y[-1])) * dt
tempy = y[-1] + (g(x[-1],y[-1])) * dt
x.append(tempx)
y.append(tempy)
return (x, y)
p1 = plt.figure(figsize=(14,7))
plt.subplots_adjust(wspace=0.23)
#-----
Z = -0.5
D=[]
for index in range(200):
random_a=random.random()
random_b=random.random()
d=calculateValue(random_a,random_b,0.001,1000)
D.append(d)
p1.add_subplot(1,2,1)
for n,m in D:
plt.plot(n,m)
plt.title("Z=-0.5",fontsize=25)
plt.ylabel("$y$",fontsize=25)
plt.xlabel("$x$",fontsize=25)
plt.tick_params(labelsize=25)
plt.xticks([0,0.2,0.4,0.6,0.8,1])
# plt.title("Phase space")
plt.grid(linestyle=":",color="b",linewidth=1)
#-----
Z = 1
D=[]
for index in range(200):
random_a=random.random()
random_b=random.random()
d=calculateValue(random_a,random_b,0.001,1000)
D.append(d)
p1.add_subplot(1,2,2)
for n,m in D:
plt.plot(n,m)
plt.title("Z=1",fontsize=25)
plt.ylabel("$y$",fontsize=25)
plt.xlabel("$x$",fontsize=25)
plt.tick_params(labelsize=25)
plt.xticks([0,0.2,0.4,0.6,0.8,1])
# plt.title("Phase space")
plt.grid(linestyle=":",color="b",linewidth=1)
plt.savefig("test",dpi=300,bbox_inches ="tight")
plt.show()效果：
从上图可以看出，随着Z的增大，鞍点E的坐标越向右上角移动，即更多的初始点会向(1,1）收敛；该规律可以通过求偏导进行验证，此处不赘述。
有问题留言或私信！