【论文笔记】KGCN:知识图谱 + 图卷积神经网络的推荐系统
Knowledge Graph Convolutional Networks for Recommender Systems
Hongwei Wang, Miao Zhao, Xing Xie, Wenjie Li, Minyi Guo.
In Proceedings of The 2019 Web Conference (WWW 2019)
论文原文(arXiv):https://arxiv.org/pdf/1904.12575v1.pdf
源码:https://github.com/hwwang55/KGCN(tensorflow / official)** https://github.com/zzaebok/KGCN-pytorch(pytorch)
1 introduction
(先日常嘲协同过滤系算法
协同过滤类的方法(CF-based methods)存在一定的不足之处,例如数据稀疏与冷启动问题。为缓解部分问题,当前大多采用知识图谱(KG)的思路,即将物品属性,用户信息,社交网络关系等多种可以辅助决策的属性(attribute)通过知识图谱的方式结合,以得到能够较好融合 side information 的网络,并同时建立各个实体之间,实体与属性之间的关系。
知识图谱,在此多以异构信息网络的形式,主要有以下几个优点:
- 利用更多的 side information 数据信息以帮助决策,可以更好地发掘用户的潜在兴趣
- 此时各个实体之间存在多种多样的关系,能够帮助提高用户推荐的多样性(diversity)
- 推荐结果具有较好的解释性
然而将知识图谱与推荐系统本身进行融合的工作本身面临诸多挑战,当前大多使用 embedding 的方法进行融合(KGE),即将各个实体与关系转化为一定维度的向量表示(主流模型参考这里),但存在训练目标与下游任务不匹配的问题:以 Trans 系算法为例,在进行 embedding 时的训练往往基于头结点,关系与尾结点的运算关系,更适用于单纯基于 KG 的下游任务,而和推荐系统最终推荐 / 点击预测的目标是不匹配的。
同理,基于路径的方法同样存在其问题,人工设计 meta-path 与 meta-graph 往往要求一定的专家建议,且有效性与全面性难以得到保证(KDD2017 这篇 就是典型的基于路径的方法,注意下游任务往往又是回到矩阵分解 / 分解因子机的)
其他方法,如 RippleNet 同样存在一定的问题(RippleNet 论文笔记戳这里):首先其降低了关系 R 的重要性,其直接的 v T R h v^TRh vTRh 的计算方式难以捕捉关系带来的信息;其次,随着整个 ripple 的范围的扩大,此时加入模型训练的实体会大幅增多,带来巨大的计算负担和冗余。
原文提出一种融合 KG 特点与图卷积神经网络的模型(KGCN),也就是在计算 KG 中某一个给定的 entity 的表示时,将邻居信息与偏差一并结合进来。主要体现出如下的优势:
- 通过邻居信息的综合,可以更好地捕捉局部邻域结构(local proximity structure)并储存在各 entity 中
- 不同邻居的权重取决于之间的关系和特定的用户 u,可以更好地体现用户的个性化兴趣,以展示 entity 的特点
2 模型解释
2.1 问题叙述
本质上还是基于知识图谱的推荐系统,考虑此时已经得到一个构造好的,由 (实体,关系,实体)的三元组组成的知识图谱,记作 G \mathcal{G} G
给定 用户 - 物品矩阵 Y Y Y(本身是一个稀疏矩阵) 和知识图谱 G \mathcal{G} G ,判断用户 u 是否会对物品 v 有兴趣,也就是需要学习到一个预测方程(prediction function): y ^ u , v = F ( u , v ∣ Θ , Y , G ) \hat{y}_{u,v} = \mathcal{F}(u,v | \text{ } \Theta,Y,\mathcal{G} ) y^u,v=F(u,v∣ Θ,Y,G),这里的 Θ \Theta Θ 定义为整个模型的学习参数的集合。
2.2 KGCN layer
符号定义:
- N ( v ) N(v) N(v):所有和实体 v 直接相连的(也就是一跳内的)所有实体的集合
- r e i , e j r_{e_i, e_j} rei,ej:实体 ei 和 ej 之间的关系
- 定义函数 g g g:某个函数,可以使得 R d × R d → R R^d \times R^d \to R Rd×Rd→R(比如内积),用来计算用户 u 和某个关系 r 之间的分数: π r u = g ( r , u ) \pi_r^u= g(r,u) πru=g(r,u),这里的 d d d 是 KG 的 embedding 表示的维度。注意这里的现实含义可以理解为(计算用户对不同的关系的偏好程度),比如某个用户非常在意影片的演员,则他对于 star 这类的 relationship 会有更多的关注,也会更愿意看他喜欢的演员的电影;而对于不是很在意演员的用户,可能对导演 director 之类的 relationship 反而有更多的帮助,这里的 g 函数即用于衡量用户对于不同关系的偏好程度。
利用邻居信息的线性组合来刻画结点 v 的邻域信息,定义为: v N ( v ) u = ∑ e ∈ N ( v ) π r v , e u e v_{N(v)}^u = \sum_{e\in N(v)}{ \pi_{r_{v,e}}^u e} vN(v)u=e∈N(v)∑πrv,eue,注意这里的权重 π \pi π 同时和(v,e 两个结点之间的关系)和(此时对应的用户 u 的特点)有关。这里的权重也就是 v 对应的 N(v) 中的所有实体 e 和关系 r 的 g 函数得分再归一化,计算如下: π r v , e u = e x p ( π r v , e u ) ∑ e ∈ N ( v ) e x p ( π r v , e u ) \pi_{r_{v,e}}^u = \frac{exp(\pi_{r_{v,e}}^u)}{\sum_{e\in N(v)} {exp(\pi_{r_{v,e}}^u)}} πrv,eu=∑e∈N(v)exp(πrv,eu)exp(πrv,eu)
个人感觉这里实际上和 KGAT 的第二部分有点像(KGAT 论文笔记),在 KGAT 中以 v 结点周围的 N(v) (这里的 N(v) 是所有以 v 为头结点的三元组的集合)中的实体 e (也就是尾节点)的线性组合来表示 v,具体计算各个 e 的权重的时候用的是注意力机制,可以理解为,此时决定权重的是在关系 r 的空间上,要被表示的头结点和尾节点的相似程度。但是这里更多地考虑了当前关系 r 对于用户 u 的重要性(通过上面的得分函数 g)
控制邻居个数:注意可能会出现某一个结点 v 存在过多的邻居的情况,会为整体的模型的计算带来巨大的压力。此时定义一个超参数 K K K,对于每一个结点 v,只是选取 K 个邻居进行计算。也就是说,此时 v 的邻域表示记作 v S ( v ) u v_{S(v)}^u vS(v)u,且满足: S ( v ) → { e ∣ e ∈ N ( v ) } , ∣ S ( v ) ∣ = K S(v) \to \lbrace e| e\in N(v)\rbrace \text{ },\text{ }\text{ } |S(v)| = \mathcal{K} S(v)→{e∣e∈N(v)} , ∣S(v)∣=K
将原 embedding 与邻域表示结合起来:这里提供了几个可以用的聚合器(aggregators):

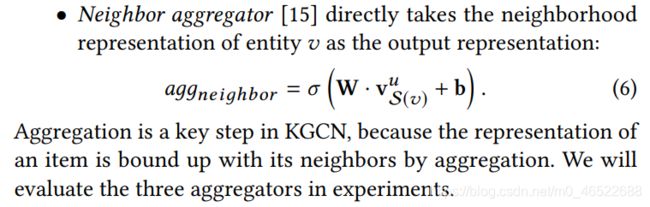
注意最后一个 neighbor 的聚合器直接就是利用邻域表示来代替 v 结点的表示。
预测层:得到各个结点的表示后,同理使用 u v 的内积搭配 sigmoid 函数作点击概率预测,就不再赘述了。
summary
下图为上面计算方法的一个示例,这里的 K = 2:
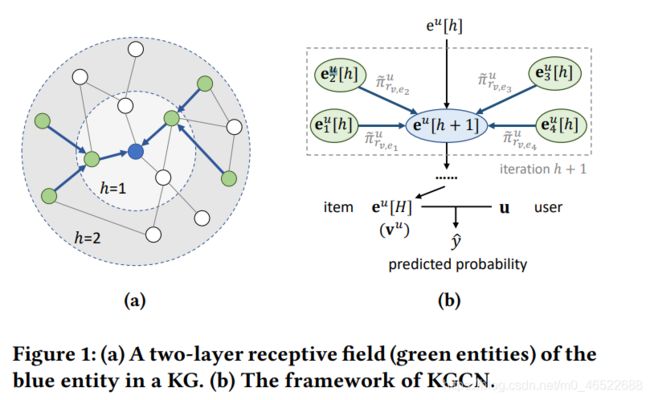
在参数迭代的过程中,比如对于第 h+1 次迭代,就是用第 h 次迭代时得到的实体 e 的 embedding 表示作为初始值,再更新计算当前结点 v 的邻域表示,再和第 h 次得到的 v 的邻域表示进行 aggregate,得到第 h+1 次结点 v 的邻域表示。
个人感觉这段就是很像 KGAT(KGAT 论文笔记),KGAT 是每轮参数迭代的时候也是通过多次迭代的方式(以一个超参数控制)融合多跳位置的信息,再扔进去预测;这里同理,比如第 2 次训练的时候,要用到 v 的邻域 e‘ 的第一次训练的结果,而 e’ 的第一次训练的结果是包含了 e’ 的再邻域的,也就是此时将 v 的二跳的 entity 的信息综合到 v 中了,也就是可以实现多跳位置的信息的捕捉。具体看后面模型学习部分的算法流程,通过一个超参数 H 来确定要吸收几跳的信息。也就是将(得到邻域表示 + 原本表示 → 融合)的过程重复 H 遍,再往下一个流程走。
此时个人感觉最大的区别还是在(邻居的权重)的计算方式上,此时是通过一个和关系,和 u 有关的得分函数 g 来计算的;而 KGAT 是通过图注意力机制,考察的是在关系 r 这个空间上,尾节点 t 和头结点 h 之间的相似程度,越相似越容易得到更大的权重,但没有考虑不同 u 对于不同 r 的偏重是不同的。
2.3 模型学习
整体模型的损失函数:

注意,在衡量的时候本身一个用户 u 没有发生过行为的物品数量是要远远大于发生过行为的物品数量的,对于类别不平衡问题,这里采用的是负采样。本质上损失函数就是交叉熵函数,前面部分是考虑了负采样的分布的交叉熵损失函数(也就是最后的推荐行为的损失函数 = 预测用户是否会点击 = 二分类问题),最后带一个 L2 正则项减轻过拟合。
整体模型的迭代过程:

这里的 M[h] 就是不断得到 v 对应的邻域,注意随着迭代的 h 的次数上升,是不断将多跳范围的信息都融合进入了 v 的 embedding 的。
3 测试
实验用的数据集:
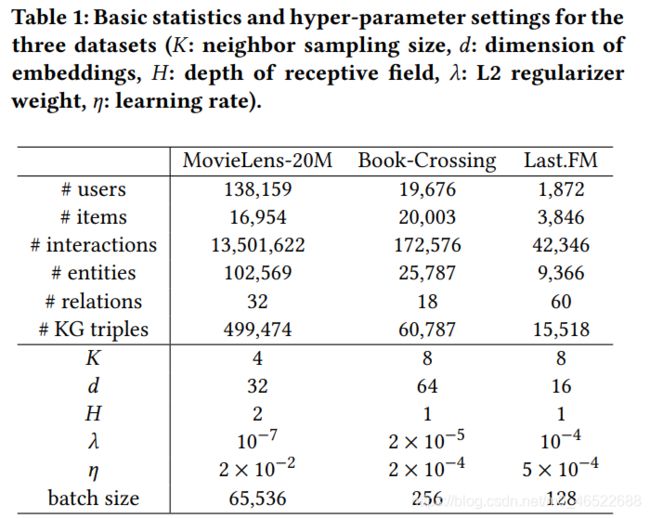
注意这里的 K 都不是很大,一般只要选择一部分的邻居来计算邻域表示本身的效果就不错。同理 H 选取也不大,如果过多跳的信息融入,一方面是计算很大,另一方面会导致重合(也就是每一个 v 都是它为中心的一大块范围的信息的融合,则不同的 v 之间会有趋同的倾向,反而是向模型中引入了噪音)。
这里用 F1 和 AUC 来评价:
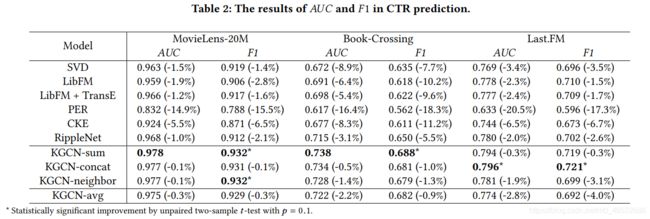
注意这里选择不同的 aggregator (上面给了三种选择)的结果还是存在一定的差异的,具体实验的时候还是都试试会比较好。
阅读仓促,存在错误 / 不足欢迎指出!期待进一步讨论~
转载请注明出处。知识见解与想法理应自由共享交流,禁止任何商用行为!