Transformer论文阅读:Attention Is All You Need
文章目录
- 前言
- 介绍
- Transformer结构
-
- Encoder
-
- 1. Multi-Head Attention
- 2. Positional Encoding
- 3. Add&Norm
- 4. Position-wise Feed-Forward Networks
- 5. Embeddings
- Decoder
-
- 1. masked multi-head attention
- 2. 连接Encoder和Decoder的部分
- 3. Linear transformation和softmax
- why self-attention
- 训练
-
- 正则化策略
前言
自己感觉不错的入门方式:先看李宏毅的self-attention和transformer的视频,理解好计算步骤;再自己去看论文更加深入地了解Transformer的架构;再看李沐的Transformer论文阅读搞清楚自己没有发现的一些点。
介绍
首先要了解seq2seq是什么东西。seq2seq简单来说就是:输入是一个序列,输出也是一个序列且输出的长度是不确定的。之前的seq2seq model的结构基本是:基于RNN或CNN的一个encoder和一个decoder,以及通过 attention machanism 连接 encoder 和 decoder。
了解RNN的都知道,RNN的输出需要上一个输出作为输入,也就是它不能做到并行处理;而且RNN无法考虑到太久以前的信息(传着传着就没了)。后来的LSTM可以处理更长的序列,但是它仍做不到并行处理。
CNN实际上算是注意力机制的一种特殊情况,它考虑的是固定范围的输入,对感受野内的值进行加权求和。
Attention mechanism(注意力机制)就像它的名字所说,它是用来计算模型输出一个东西的时候应该更加注意哪些输入。举个例子:翻译 “hello world”,输出第一二个字“你好”时,注意力机制就要求模型更加关注 “hello” 这个词。它可以在 不用考虑输入与输出的情况下 计算输出和输入的相关性,为并行化提供了条件。
但是之前的模型都是把注意力机制跟循环网络一起用的,导致无法并行化。所以 Transformer 抛弃了循环网络,完全使用注意力机制,从而实现了并行化,且效果达到了最佳。
Transformer使用的是 self-attention(自注意力机制),就是用输入计算权重,再对输入进行加权求和(后面会讲)。
Transformer结构

Transformer仍然使用 encoder-decoder 架构。图中左边为 encoder 的一个block,右边为 decoder 的一个 block,一个 encoder/decoder 由N(N=6)个这样的blocks组成。
Encoder
Encoder的一个block的结构:输入进入embedding layer得到 input embedding,再加上一个 positional encoding 输入 multi-head attention 中,经过 add&norm 后再输入全连接的 feed forward,再输入 add&norm。
下面一一介绍每一部分。
1. Multi-Head Attention
再介绍多头注意力机制前,得先知道单头自注意力机制是怎么算的。
一、单头注意力机制
常见的自注意力机制有两种,一种是 addtive attention,一种是 dot-product attention(需要向量queries和keys维度相同)。它们的效果差不多,但是 dot-product attention 只需要做矩阵乘法,计算更简单,所以论文使用第二种。
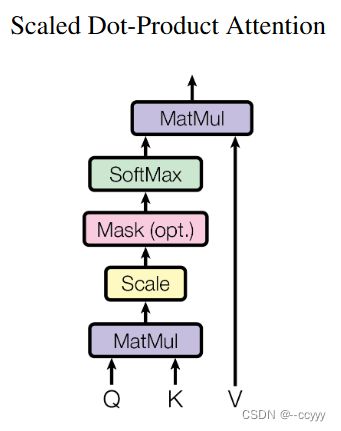
上面的图就是 scaled dot-product attention 的计算方式。那Q, K, V是什么呢,接下来讲。
矩阵Q, K, V分别表示query, key, value,它们都是用输入的矩阵乘以矩阵 W Q , W K , W V W^Q, W^K, W^V WQ,WK,WV计算来的。从它们的意思直观理解,queries就是想要问询一个输入与每个输入有多大关系;keys就是每个输入对应的关键信息,用来给queries计算相关程度的;values就是queries计算完相关程度后,用来加权求和的值。
假设有n个输入,那么每个输入会对应一个query vector q i q_i qi、一个key vector k i k_i ki、一个value vector v i v_i vi,它们组成矩阵Q, K, V,维度分别为 n × d k n\times d_k n×dk, n × d k n\times d_k n×dk, n × d v n\times d_v n×dv。
① 先用 q i q_i qi 和 k j k_j kj 做内积得到attention scores,也即 A = Q K T A = QK^T A=QKT;
② 再除以 d k \sqrt{d_k} dk,做scaled;这里要做scaled的原因是:当 d k d_k dk较大时,dot-product attention的效果会变差。这是因为值太大时softmax的梯度会消失,所以要做scaled。
③ 做softmax: A ′ = s o f t m a x ( A d k ) A' = softmax(\frac{A}{\sqrt{d_k}}) A′=softmax(dkA),得到attention scores;
④ 最后做加权求和: A t t e n t i o n ( Q , K , V ) = A ′ V Attention(Q, K, V)=A'V Attention(Q,K,V)=A′V。输出的维度为 n × d v n\times d_v n×dv,每一行代表一个输入。
二、多头自注意力机制
单头的只能提取到一种相关性,为了提取多种相关性,就使用多头(multi head)的。

从图中可以看出,multi-head就是把Q, K, V分别做线性映射成h个矩阵,再对这些矩阵分别做h次single-head,最后再concat在一起后做线性映射。
用公式来表示就是:
h e a d i = A t t e n t i o n ( Q W i Q , K W i K , V W i V ) , i = 1 , 2 , . . . , h head_i=Attention(QW_i^Q, KW_i^K, VW_i^V), i=1, 2, ..., h headi=Attention(QWiQ,KWiK,VWiV),i=1,2,...,h
M u l t i H e a d ( Q , K , V ) = C o n c a t ( h e a d 1 , . . . , h e a d h ) W O MultiHead(Q, K, V)=Concat(head_1, ..., head_h)W^O MultiHead(Q,K,V)=Concat(head1,...,headh)WO
其中 Q , K , V Q, K, V Q,K,V维度都为 n × d m o d e l n\times d_{model} n×dmodel, W i Q , W i K W_i^Q, W_i^K WiQ,WiK维度为 d m o d e l × d k d_{model}\times d_k dmodel×dk, W i V W_i^V WiV维度为 d m o d e l × d v d_{model}\times d_v dmodel×dv, W O W^O WO维度为 h d v × d m o d e l hd_v\times d_{model} hdv×dmodel。最后输出维度为 n × d m o d e l n\times d_{model} n×dmodel。
因为multi-head要把Q, K, V分解成 h 个部分,那自然地认为 q i , k i , v i q_i, k_i, v_i qi,ki,vi 的特征维度应该增加 h 倍,所以论文取 d k = d v = d m o d e l / h = 64 d_k=d_v=d_{model}/h=64 dk=dv=dmodel/h=64。
2. Positional Encoding
从上面的自注意力机制介绍中可以看到,序列是全部一起输入的,并没有考虑到序列的顺序。所以加了一个positional encoding,让输入带有位置的信息。
这个东西既可以自己设定,也可以从网络中学出来。两个的效果差不多,而自己设定的可以不用在意序列长度。所以论文采用自己设定的正弦和余弦函数:
P E ( p o s , 2 i ) = s i n ( p o s / 1000 0 2 i / d m o d e l ) PE_{(pos, 2i)}=sin(pos/10000^{2i/d_{model}}) PE(pos,2i)=sin(pos/100002i/dmodel)
P E ( p o s , 2 i + 1 ) = c o s ( p o s / 1000 0 2 i / d m o d e l ) PE_{(pos, 2i+1)}=cos(pos/10000^{2i/d_{model}}) PE(pos,2i+1)=cos(pos/100002i/dmodel)
其中pos表示位置,i表示第i个维度,postional encoding的维度也是 d m o d e l d_{model} dmodel。
之所以用正弦余弦函数,是因为论文认为它们可以让模型很好地学到如何让相关位置参与到 attention scores 的计算中(因为可以证明, P E p o s + k PE_{pos+k} PEpos+k可以表示为 P E p o s PE_{pos} PEpos的线性方程)。
3. Add&Norm

公式表示就是: L a y e r N o r m ( x + S u b l a y e r ( x ) ) LayerNorm(x+Sublayer(x)) LayerNorm(x+Sublayer(x))。
这里的Add就是残差连接(ResNet),为了防止梯度消失的。把self-attention的输入加到它的输出上。
Norm不是batch norm,而是用layer norm,主要是因为NLP本身的性质:它是处理语句的。
下面一张图就可以说清楚它们的区别:
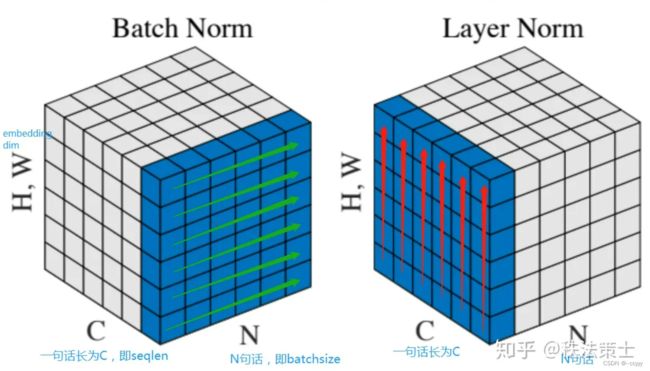
(图来源:https://zhuanlan.zhihu.com/p/74516930)
每个句子的长度是不同的,如果对同一个位置的词进行归一化,明显是不合理的。而layer norm是对一句话进行归一化。
4. Position-wise Feed-Forward Networks
这是由两个线性变换和一个ReLU组成的,写作公式是: F F N ( x ) = m a x ( 0 , x W 1 + b 1 ) W 2 + b 2 FFN(x)=max(0, xW_1+b_1)W_2+b_2 FFN(x)=max(0,xW1+b1)W2+b2。输入和输出维度都是 d m o d e l = 512 d_{model}=512 dmodel=512,中间层的维度是2048。
5. Embeddings
前面说了,Embeddings是把输入的每个词转成维度为 d m o d e l d_{model} dmodel的向量。
论文提到,这里跟decoder的Embeddings、decoder最后的linear transformation共享同一个权重矩阵,不过两个embedding layers的权重还要乘上 d m o d e l \sqrt{d_{model}} dmodel。要乘上的原因是为了与后面加上的positional encoding(绝对值范围是0到1)的大小相差的不多。
Decoder
接下来将Decoder的结构。
Decoder的一个block结构与encoder的差不多,就是多出了一块连接decoder和encoder的部分,以及最开始的multi-head attention是masked的。
1. masked multi-head attention
Decoder的输入并不是像Encoder一样把整个句子一次性输入的。它是auto-regressive(自回归)的,举个例子:翻译,第一次先输入 ‘[BEGIN]’,decoder输出预测第一个词 ‘机’;第二次把 ‘[BEGIN]’ ‘机’ 都作为输入,decoder输出预测的第二个词 ‘器’… 知道decoder预测词为 '[END]‘。
所以decoder只能看到此时的time-step之前的单词,也就是要把此时以及之后的单词遮住(mask),加权求和的values只使用此时time-step之前的词对应的values。就是 softmax后的attention scores矩阵 A ′ A' A′的形式会是一个下三角矩阵:
( o 1 o 2 o 3 o 4 ) = ( α 1 , 1 ′ 0 0 0 α 2 , 1 ′ α 2 , 2 ′ 0 0 α 3 , 1 ′ α 3 , 2 ′ α 3 , 3 ′ 0 α 4 , 1 ′ α 4 , 2 ′ α 4 , 3 ′ α 4 , 4 ′ ) ( v 1 v 2 v 3 v 4 ) \begin{pmatrix} o^1\\ o^2\\ o^3\\ o^4 \end{pmatrix}= \begin{pmatrix} \alpha_{1,1}^{'} & 0&0&0\\ \alpha_{2,1}^{'} & \alpha_{2,2}^{'}&0&0\\ \alpha_{3,1}^{'} & \alpha_{3,2}^{'}&\alpha_{3,3}^{'}&0\\ \alpha_{4,1}^{'} & \alpha_{4,2}^{'}&\alpha_{4,3}^{'}&\alpha_{4,4}^{'}\\ \end{pmatrix} \begin{pmatrix} v^1\\ v^2\\ v^3\\ v^4 \end{pmatrix} ⎝⎜⎜⎛o1o2o3o4⎠⎟⎟⎞=⎝⎜⎜⎜⎛α1,1′α2,1′α3,1′α4,1′0α2,2′α3,2′α4,2′00α3,3′α4,3′000α4,4′⎠⎟⎟⎟⎞⎝⎜⎜⎛v1v2v3v4⎠⎟⎟⎞
那要使得softmax后的值变为0,就只要在softmax前把attention scores矩阵 A A A对应位置的值设为 − ∞ -\infty −∞就好。
2. 连接Encoder和Decoder的部分
这部分的multi-head attention的输入keys, values来自Encoder的输出,queries来自decoder前面的输出。计算方式跟前面是一样的。
3. Linear transformation和softmax
最后一部分没什么好说的,就是权重矩阵是与两个embedding layers共享的。输出的是预测每个词对应的概率,最后取概率最大的就得到预测的词。
why self-attention

论文分析了问什么使用自注意力机制比RNN、CNN好。
① 首先是每一层的计算复杂度。
设n为序列长度,d为representation的维度,k是kernel size,r是限制的self-attention的领域大小。
self-attention每一层就是矩阵与矩阵相乘,时间复杂度为 O ( n 2 ⋅ d ) O(n^2\cdot d) O(n2⋅d);RNN每一步计算时间复杂度为 O ( d 2 ) O(d^2) O(d2),共n步,总共是 O ( n ⋅ d 2 ) O(n\cdot d^2) O(n⋅d2);CNN做卷积计算复杂度为 ( k ⋅ n ⋅ d 2 ) (k\cdot n \cdot d^2) (k⋅n⋅d2);限制的self-attention计算复杂度为 O ( r ⋅ n ⋅ d ) O(r\cdot n\cdot d) O(r⋅n⋅d)。
大多数时候n比d小,所以self-attention每一层的计算会比RNN CNN快。
② 计算的并行度。
RNN计算完整个序列需要n步,其他都是一步到位。
③ the length of the paths forward and backward signals have to traverse in the network.
在别的地方看到一个很好的说法:叫做全局感受野所需网络层数。这个指标就是衡量模型能不能很好地捕捉到很久以前的信息。
self-attention输入是一整个序列一起输入的,看到整个序列只需要一层;而RNN需要走n步才能看到完整的输入信息。
训练
论文训练使用的是Adam优化器,学习率的变化是在前 warmup_steps 逐步上升,随后逐渐减小:
l r a t e = d m o d e l − 0.5 ⋅ m i n ( s t e p n u m − 0.5 , s t e p n u m ⋅ w a r m u p s t e p s − 1.5 ) lrate=d^{-0.5}_{model}\cdot min(stepnum^{-0.5}, stepnum\cdot warmupsteps^{-1.5}) lrate=dmodel−0.5⋅min(stepnum−0.5,stepnum⋅warmupsteps−1.5)
这个学习率的变化挺关键的,不这样设置训练不出很好的模型。
正则化策略
在每个 add&norm 输入之前都做一次dropout;还有在 embeddings 和 positional encodings 相加时也做dropout。
在softmax的时候使用label smoothing。