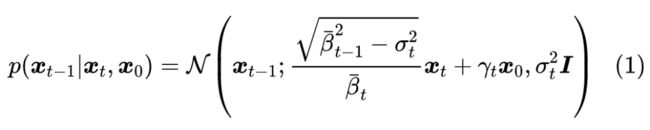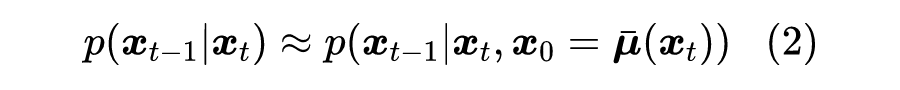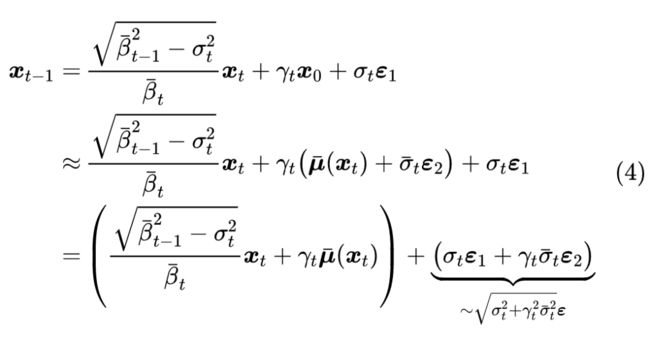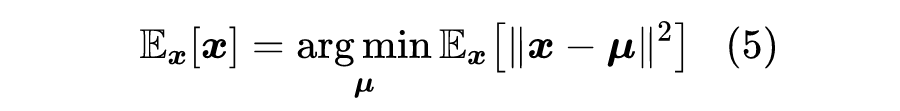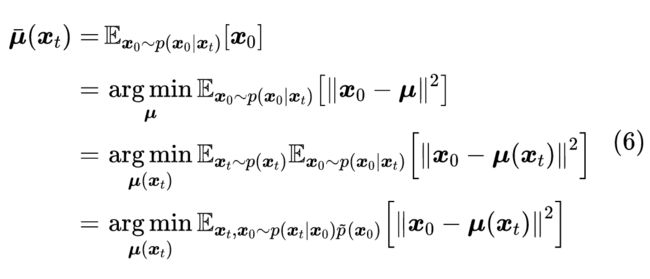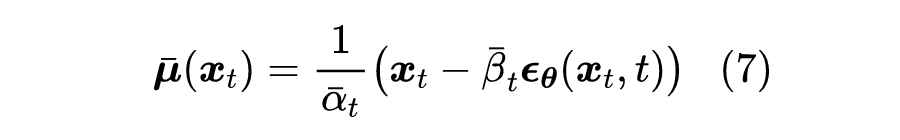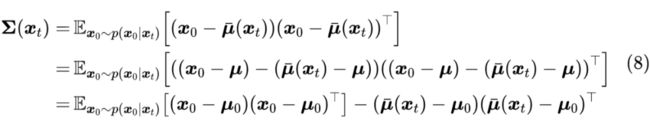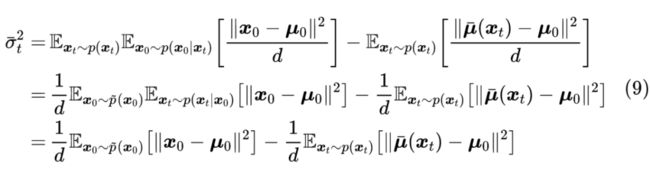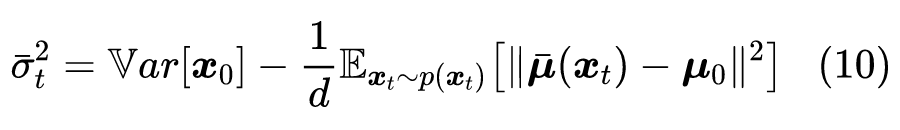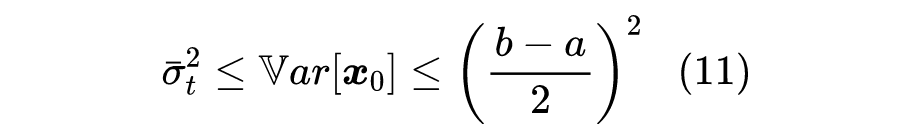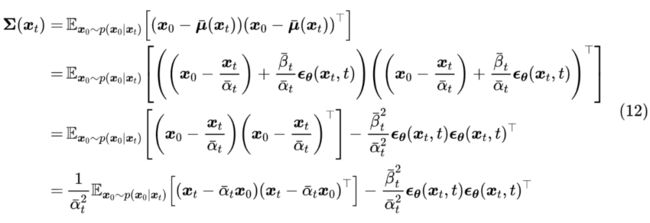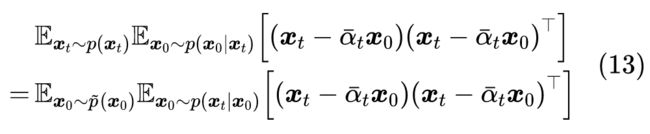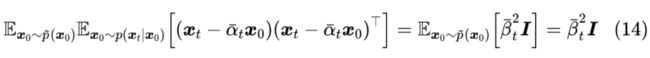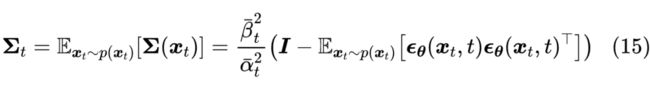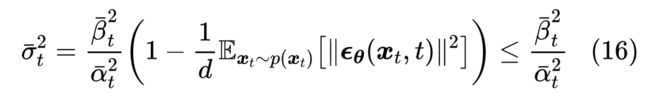生成扩散模型漫谈：最优扩散方差估计（上）

©PaperWeekly 原创 · 作者 | 苏剑林

单位 | 追一科技

研究方向 | NLP、神经网络

对于生成扩散模型来说，一个很关键的问题是生成过程的方差应该怎么选择，因为不同的方差会明显影响生成效果。

在《生成扩散模型漫谈：DDPM = 自回归式 VAE》我们提到，DDPM 分别假设数据服从两种特殊分布推出了两个可用的结果；《生成扩散模型漫谈：DDIM = 高观点DDPM》中的 DDIM 则调整了生成过程，将方差变为超参数，甚至允许零方差生成，但方差为 0 的 DDIM 的生成效果普遍差于方差非 0 的 DDPM；而《生成扩散模型漫谈：一般框架之 SDE 篇》显示前、反向 SDE 的方差应该是一致的，但这原则上在 时才成立；《Improved Denoising Diffusion Probabilistic Models》则提出将它视为可训练参数来学习，但会增加训练难度。

所以，生成过程的方差究竟该怎么设置呢？今年的两篇论文《Analytic-DPM: an Analytic Estimate of the Optimal Reverse Variance in Diffusion Probabilistic Models》和《Estimating the Optimal Covariance with Imperfect Mean in Diffusion Probabilistic Models》算是给这个问题提供了比较完美的答案。接下来我们一起欣赏一下它们的结果。

不确定性

事实上，这两篇论文出自同一团队，作者也基本相同。第一篇论文（简称 Analytic-DPM）下面简称在 DDIM 的基础上，推导了无条件方差的一个解析解；第二篇论文（简称 Extended-Analytic-DPM）则弱化了第一篇论文的假设，并提出了有条件方差的优化方法。本文首先介绍第一篇论文的结果。

在《生成扩散模型漫谈：DDIM = 高观点 DDPM》中，我们推导了对于给定的 ，对应的 的一般解为

其中 ， 就是可调的标准差参数。在 DDIM 中，接下来的处理流程是：用 来估计 ，然后认为

然而，从贝叶斯的角度来看，这个处理是非常不妥的，因为从 预测 不可能完全准确，它带有一定的不确定性，因此我们应该用概率分布而非确定性的函数来描述它。事实上，严格地有

精确的 通常是没法获得的，但这里只要一个粗糙的近似，因此我们用正态分布 去逼近它（如何逼近我们稍后再讨论）。有了这个近似分布后，我们可以写出：

其中 。可以看到， 更加接近均值为 、协方差为 的正态分布，其中均值跟以往的结果是一致的，不同的是方差多出了 这一项，因此即便 ，对应的方差也不为0。多出来的这一项，就是第一篇论文所提的最优方差的修正项。

均值优化

现在我们来讨论如何用 去逼近真实的 ，说白了就是求出 的均值和协方差。

对于均值 来说，它依赖于 ，所以需要一个模型来拟合它，而训练模型就需要损失函数。利用

我们得到

这就是训练 所用的损失函数。如果像之前一样引入参数化

就可以得到 DDPM 训练所用的损失函数形式 了。关于均值优化的结果是跟以往一致的，没有什么改动。

方差估计1

类似地，根据定义，协方差矩阵应该是

其中 可以是任意常向量，这对应于协方差的平移不变性。

上式估计的是完整的协方差矩阵，但并不是我们想要的，因为目前我们是想要用 去逼近 ，其中设计的协方差矩阵为 ，它有两个特点：

1、跟 无关：为了消除对 的依赖，我们对全体 求平均，即 ；

2、单位阵的倍数：这意味着我们只用考虑对角线部分，并且对对角线元素取平均，即 ，其中 。

于是我们有

这是笔者给出的关于 的一个解析形式，在 完成训练的情况下，可以通过采样一批 和 来近似计算上式。

特别地，如果取 ，那么刚好可以写成

这里的 是全体训练数据 的像素级方差。如果 的每个像素值都在 区间内，那么它的方差显然不会超过 ，从而有不等式

方差估计2

刚才的解是笔者给出的、认为比较直观的一个解，Analytic-DPM 原论文则给出了一个略有不同的解，但笔者认为相对来说没那么直观。通过代入式（7），我们可以得到：

此时如果两端对 求平均，我们有

别忘了 ，所以 实际上就是 的均值，那么 实际上是在求 的均值的协方差矩阵，结果显然就是 ，所以

那么

两边取迹然后处以 ，得到

这就得到了另一个估计和上界，这就是 Analytic-DPM 的原始结果。

实验结果

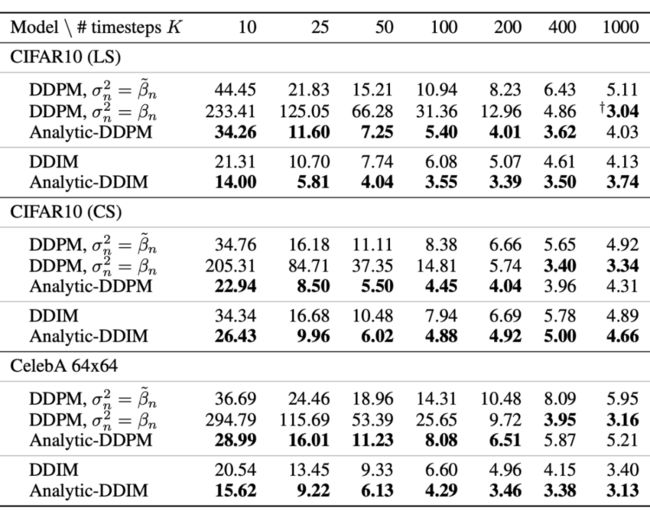
原论文的实验结果显示，Analytic-DPM 所做的方差修正，主要在生成扩散步数较少时会有比较明显的提升，所以它对扩散模型的加速比较有意义：

▲ Analytic-DPM 主要在扩散步数较少时会有比较明显的效果提升

笔者也在之前自己实现的代码上尝试了Analytic-DPM 的修正，参考代码为：

Github：

https://github.com/bojone/Keras-DDPM/blob/main/adpm.py 

当扩散步数为 10 时，DDPM 与 Analytic-DDPM 的效果对比如下图：

▲ DDPM 在扩散步数为 10 时的生成结果

▲ Analytic-DDPM 在扩散步数为 10 时的生成结果

可以看到，在扩散步数较小时，DDPM 的生成效果比较光滑，有点“重度磨皮”的感觉，相比之下 Analytic-DDPM 的结果显得更真实一些，但是也带来了额外的噪点。从评价指标来说，Analytic-DDPM 要更好一些。

吹毛求疵

至此，我们已经完成了 Analytic-DPM 的介绍，推导过程略带有一些技巧性，但不算太复杂，至少思路上还是很明朗的。如果读者觉得还是很难懂，那不妨再去看看原论文在附录中用 7 页纸、13 个引理完成的推导，想必看到之后就觉得本文的推导是多么友好了哈哈～

诚然，从首先得到这个方差的解析解来说，我为原作者们的洞察力而折服，但不得不说的是，从“事后诸葛亮”的角度来说，Analytic-DPM 在推导和结果上都走了一些的“弯路”，显得“太绕”、”太巧“，从而感觉不到什么启发性。其中，一个最明显的特点是，原论文的结果都用了 来表达，这就带来了三个问题：一来使得推导过程特别不直观，难以理解“怎么想到的”；二来要求读者额外了解得分匹配的相关结果，增加了理解难度；最后落到实践时， 又要用回 或 来表示，多绕一道。

本文推导的出发点是，我们是在估计正态分布的参数，对于正态分布来说，矩估计与最大似然估计相同，因此直接去估算相应的均值方差即可。结果上，没必要强行在形式上去跟 、得分匹配对齐，因为很明显 Analytic-DPM 的 baseline 模型是 DDIM，DDIM 本身就没有以得分匹配为出发点，增加与得分匹配的联系，于理论和实验都无益。直接跟 或 对齐，形式上更加直观，而且更容易跟实验形式进行转换。

文章小结

本文分享了论文 Analytic-DPM 中的扩散模型最优方差估计结果，它给出了直接可用的最优方差估计的解析式，使得我们不需要重新训练就可以直接应用它来改进生成效果。笔者用自己的思路简化了原论文的推导，并进行了简单的实验验证。

更多阅读

#投 稿 通 道#

 让你的文字被更多人看到 

如何才能让更多的优质内容以更短路径到达读者群体，缩短读者寻找优质内容的成本呢？答案就是：你不认识的人。

总有一些你不认识的人，知道你想知道的东西。PaperWeekly 或许可以成为一座桥梁，促使不同背景、不同方向的学者和学术灵感相互碰撞，迸发出更多的可能性。 

PaperWeekly 鼓励高校实验室或个人，在我们的平台上分享各类优质内容，可以是最新论文解读，也可以是学术热点剖析、科研心得或竞赛经验讲解等。我们的目的只有一个，让知识真正流动起来。

 稿件基本要求：

• 文章确系个人原创作品，未曾在公开渠道发表，如为其他平台已发表或待发表的文章，请明确标注 

• 稿件建议以 markdown 格式撰写，文中配图以附件形式发送，要求图片清晰，无版权问题

• PaperWeekly 尊重原作者署名权，并将为每篇被采纳的原创首发稿件，提供业内具有竞争力稿酬，具体依据文章阅读量和文章质量阶梯制结算

 投稿通道：

• 投稿邮箱：[email protected] 

• 来稿请备注即时联系方式（微信），以便我们在稿件选用的第一时间联系作者

• 您也可以直接添加小编微信（pwbot02）快速投稿，备注：姓名-投稿

△长按添加PaperWeekly小编

现在，在「知乎」也能找到我们了

进入知乎首页搜索「PaperWeekly」

点击「关注」订阅我们的专栏吧

·

·