全连接神经网络拟合余弦函数曲线
前面一些概念性知识可参考全连接神经网络详解
全连接神经网络是一种多层的感知机结构,层与层之间需要包括一个非线性激活函数。每一层的每一个节点都与上下层节点全部连接,这就是”全连接“的由来。整个全连接神经网络分为输入层、隐藏层和输出层,其中隐藏层可以更好的分离数据的特征,但是过多的隐藏层会导致过拟合问题。
模型训练的常用方法是反向传播(BP)算法。可以根据输出层的调整量来推导网络突触权重的调整方式,将误差进行反向传播。
设计一个全连接神经网络(MLP),训练它,拟合余弦函数曲线
#导入所需的库
import numpy as np
import matplotlib.pyplot as plt
import torch
from torch.utils.data import TensorDataset
from torch.utils.data import DataLoader
import torch.nn as nn
import torch.optim as optim数据拟合
x = np.linspace(-2*np.pi,2*np.pi,400)
y = np.cos(x) #x,y输出均为(400,)
X = np.expand_dims(x,axis = 1) #转变x,y的输出
Y = y.reshape(400,-1) #X,Y输出均为(400,1)
#把独立的数据利用Pytorch提供的TensorDataset转化为tensor类型的数据集
dataset = TensorDataset(torch.tensor(X,dtype=torch.float),torch.tensor(Y,dtype=torch.float))
#分批加载数据集中的数据到内存/显存
dataloader = DataLoader(dataset,batch_size = 10,shuffle = True)设计MLP网络模型,该网络模型包含三个隐藏层,一个输出层
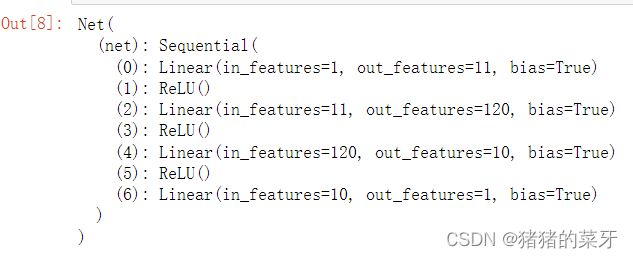
#设置网络模型,设定三个隐藏层、一个输出层
class Net(nn.Module): #定义网络模型
def __init__(self): #初始化
super(Net,self).__init__() #父类初始化
self.net = nn.Sequential(
nn.Linear(in_features=1,out_features=11),nn.ReLU(),
nn.Linear(11,120),nn.ReLU(),
nn.Linear(120,10),nn.ReLU(),
nn.Linear(10,1)
)
def forward(self,input:torch.FloatTensor):
return self.net(input)net=Net()
net设置损失函数和优化器
Loss = nn.MSELoss()
optim = optim.Adam(net.parameters(),lr = 0.001)训练网络模型,并根据训练好的模型得到预测结果值
for epoch in range(100):
loss = None
for batch_x,batch_y in dataloader:
y_predict = net(batch_x)
loss = Loss(y_predict,batch_y)
optim.zero_grad() #在进行新一轮训练之前,把上一轮用过的梯度清空
loss.backward() #损失反向传播,得到新的网络参数
optim.step() #把上一轮得到的新的网络参数更新到网络模型中
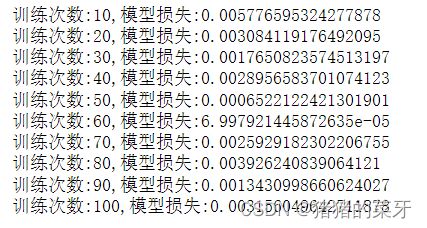
if(epoch+1)%10==0:
print('训练次数:{0},模型损失:{1}'.format(epoch+1,loss.item())) #.item把仅含一个元素的张量中的值拿出来通过可视化的方法,绘制由训练模型得到的预测值和真实值的曲线图,由此验证模型的有效性
plt.figure(figsize=(12,8))
plt.plot(x,y,label='real value',marker = 'o')
plt.plot(x,predict.detach().numpy(),label='predict value',marker = '*',c = 'r')
plt.legend()通过调整参数,可使模型训练更贴合真实余弦函数曲线。