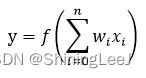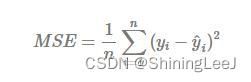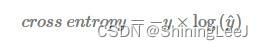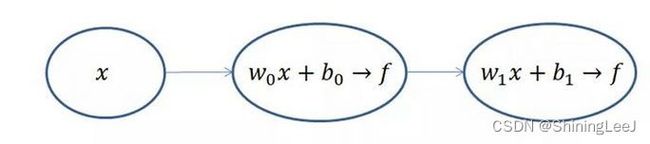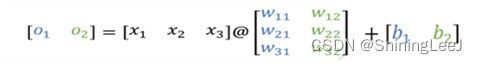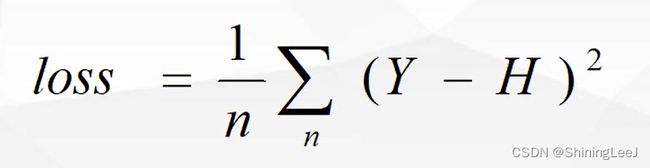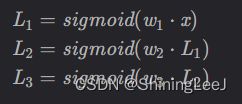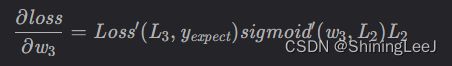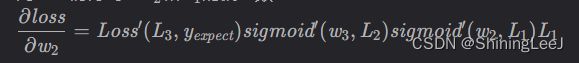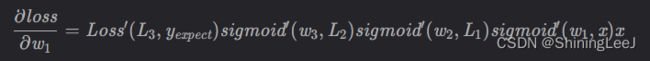全连接神经网络详解

深度学习

        在了解全连接神经网络之前，我们需要先明确什么是设密度学习。深度学习来源于仿生学，是机器学习领域中的一个研究方向。

        深度学习是通过学习样本数据的内在规律，让机器能够像人一样具有分析学习能力，能够识别图像，文字，声音等数据。

        机器学习：数据输入 --> 人工特征提取 --> 分类 --> 输出

        深度学习：数据输入 --> 神经网络特征提取和分类 --> 输出

神经元&感知机

神经元

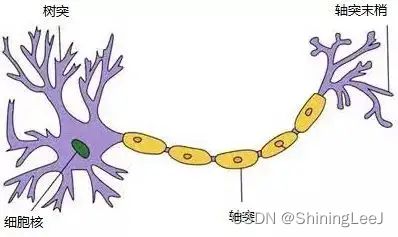
        在上面我们提到深度学习来源于仿生学，其实就是来源于神经元。树突对应输入，轴突对应中间计算过程，而轴突末梢就代表输出。

 感知机

与神经元相对应，创建了与之结构相对应的感知机。

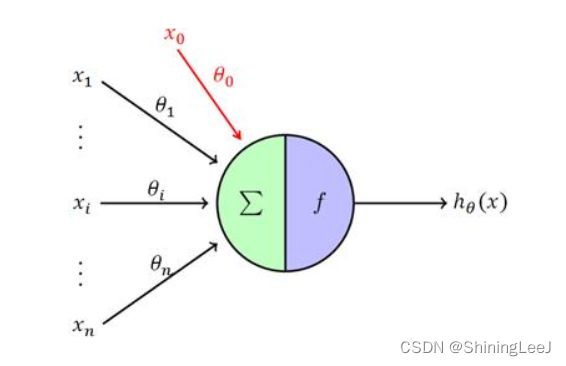
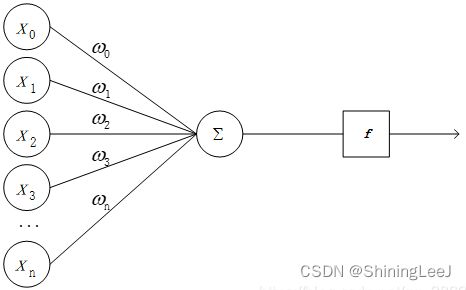
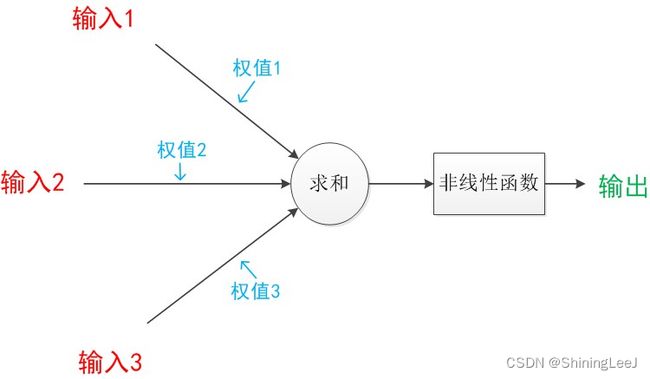
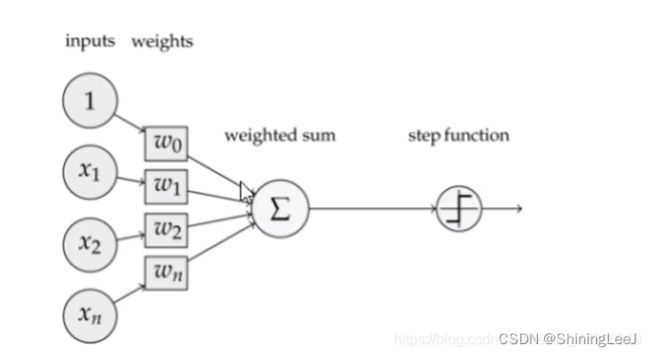
 感知机模型

        感知机模型是神经元的建模，是将输入值映射到输出值的一个数学函数。有n个输入值，分别是x1, x2, x3 … xn，对应的是权重是w1, w2, w3 … wn，则输出值为y。

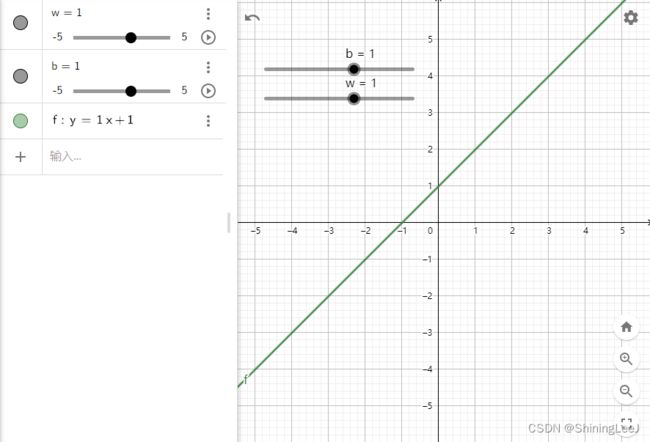
 感知机模型推演：Calculator Suite - GeoGebra

 

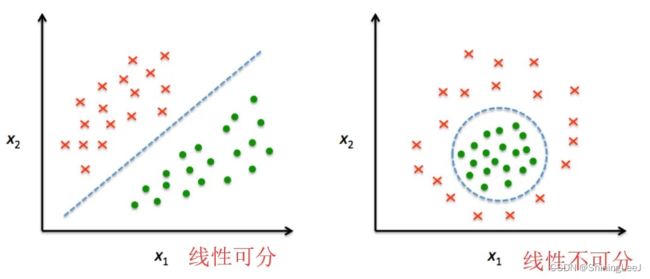
在感知机模型之中，仅能解决线性可分的问题，但是在现实生活中，大多数问题都是线性不可分的

 这就需要我们利用激活函数对线性的函数进行激活来解决非线性的问题

激活函数

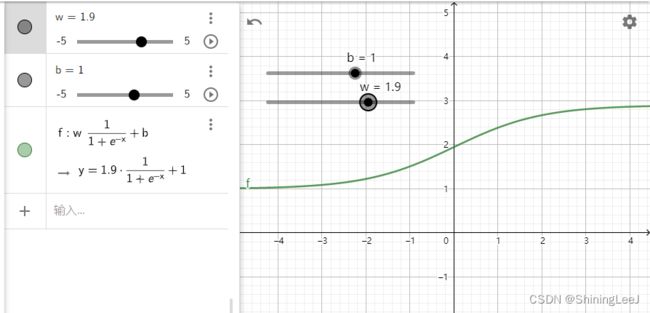
        如上面的图所示，当线性函数没有经过激活函数时，仅能解决线性的问题。但当线性的函数经过sigmoid激活函数后，则变为了非线性的函数，可以去解决非线性的问题。

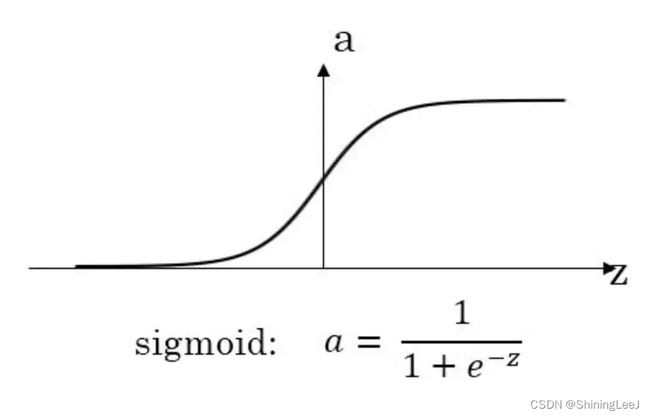
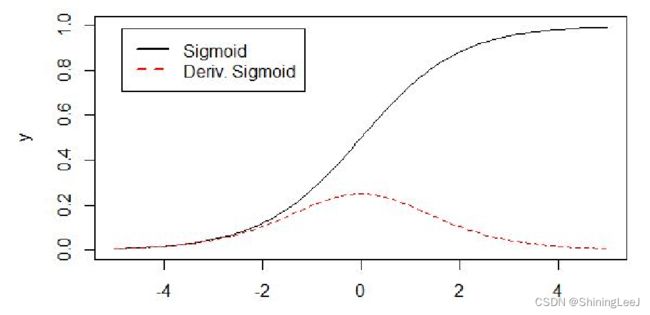
sigmoid函数

        多用于二分类问题，作为输出层，表示概率（并不是表示真实的概率，只是表达概率相对的大小）

但是sigmoid函数有一个致命的缺点：容易造成梯度消失问题（反向传播链式求导）

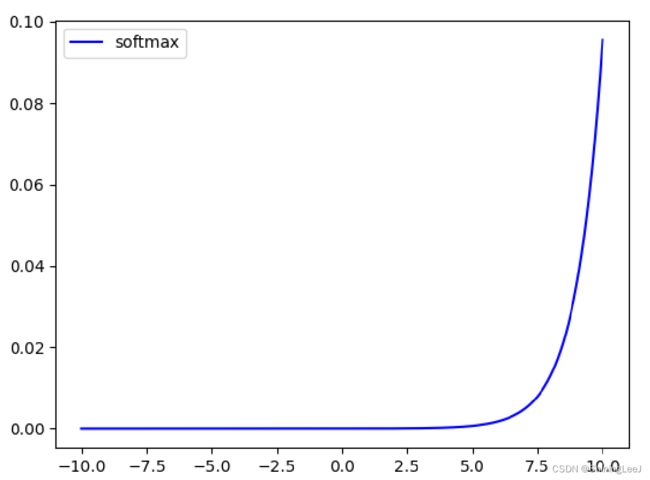
 softmax函数

        在多分类问题中，通常使用softmax函数作为激活函数，它可以对输出值进行归一化操作，把所有输出值都转化为概率，所有概率值加起来等于1。

 

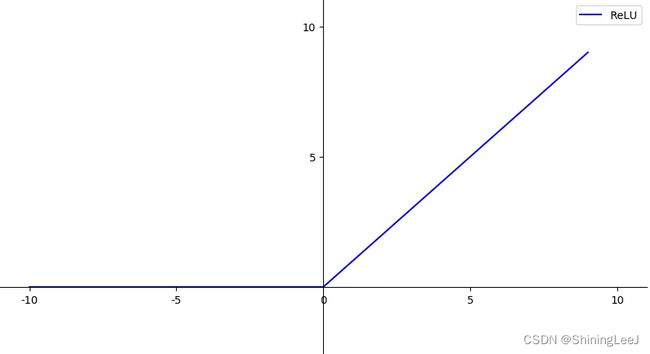
 ReLU函数

不存在梯度消失问题，是使用最频繁的激活函数

损失函数

​        深度学习是一种有监督的学习。在前向计算得到计算结果后，需要与**标签**进行对比得到计算结果与答案之间的差异，而这个差异就是损失。

​        注意：当计算结果与标签之间计算损失时，得到的损失可能为正，也可能为负。一定要将损失函数转化为整数，这样才方便对损失进行对比。

均方差损失函数

​        均方差损失函数属于是一个万金油的损失函数，既可以处理分类问题，也可以处理回归问题。

交叉熵损失函数

​        一个良好的神经网络要尽量保证对于每一个输入数据，神经网络所预测类别分布概率与实际类别分布概率之间的差距越小越好，即交叉熵越小越好。

​        交叉熵损失函数是专门用于分类问题，也可以用于回归问题，但是效果并不是很出色。

​        衡量两个概率分布之间的距离

注意：PyTorch中的交叉熵损失函数**自带了one-hot标签处理

# 自带Softmax输出函数，多分类交叉熵
nn.CrossEntropyLoss()
#  自带Sigmoid输出函数，二分类交叉熵
nn.BCEWithLogitsLoss()
# 不带输出函数的二分类交叉熵，需要用Sigmoid()激活
nn.BCELoss()
# 不带输出函数的多分类交叉熵，需要用Softmax()激活
nn.NLLLoss()

 全连接神经网络

        上面介绍了深度学习中的一些基本概念，包括感知机，激活函数等。下面就开始正式介绍全连接神经网络。

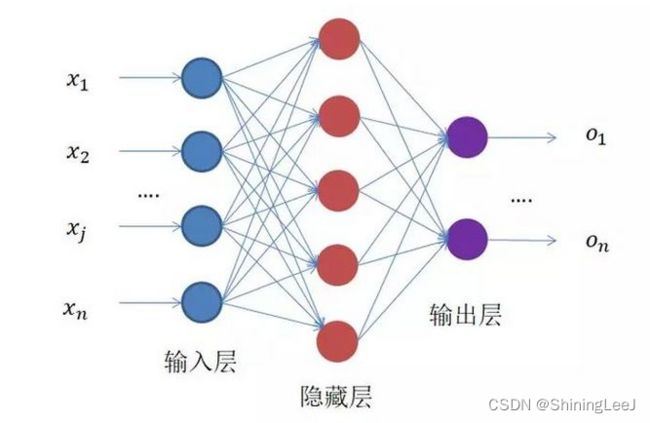
        全连接神经网络是一种多层的感知机结构。每一层的每一个节点都与上下层节点全部连接，这就是”全连接“的由来。整个全连接神经网络分为输入层，隐藏层和输出层，其中隐藏层可以更好的分离数据的特征，但是过多的隐藏层会导致过拟合问题。

 神经网络体验：A Neural Network Playground

单层神经网络

        了解了基本的概念，通过最简单的单层神经网络来了解深度学习的工作全过程。

感知机模型+激活函数输出

前向传播 （FP传播）

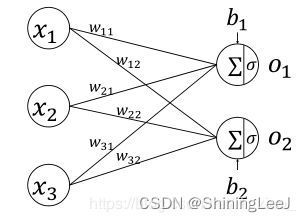
        通过输入层输入，一路前向计算，通过输出层输出的结果。如图指的是x1、x2、xn、与权重（w）相乘，然后进行求和，最后通过激活函数输出结果，这个过程就是前向传播。

         不算输入层，上面的网络结构总共有两层，隐藏层和输出层，它们“圆圈”里的计算都是下面公式的计算组合：

 线性变换：加权和偏置

非线性变换：激活函数

损失函数

        神经网络是一种监督性的学习，前向传播得到结果后，与标签进行对比，得到的差异就称为损失。损失函数有多种，这里只是列举了其中的一种。

        计算的到的损失可能有正数或者负数存在，无法准确的判断与标签的差异，所以需要将损失变为正数。

 Y为标准值，H为前向传播值

反向传播

（BP算法反向传播目的就是让损失降到最低。我们来看损失函数的公式：

                

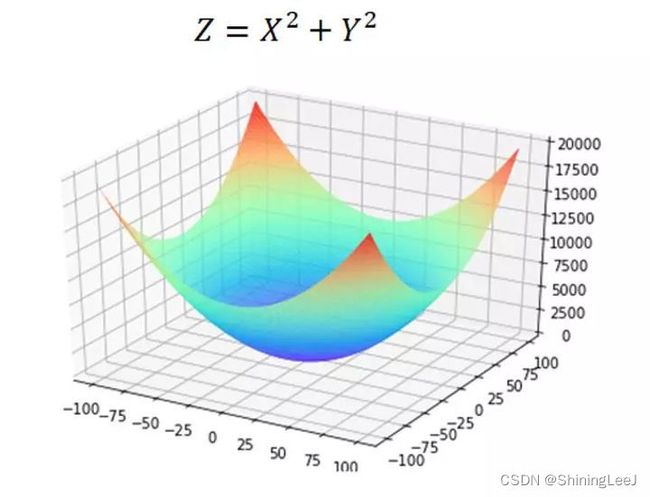
        其中的w和b为未知参数，这就是反向传播需要去更新的参数。将loss的公式进行简化，得到下面的公式和图像，为了让损失降到最低，其实就是要让最佳的位置到达图像的最底部（相当于是碗底）

         下面就来解决如何让损失到达“碗底”。这里的公式里面有两个参数，不方便进行理解，将其中一个参数作为常数，再来对图像进行研究。

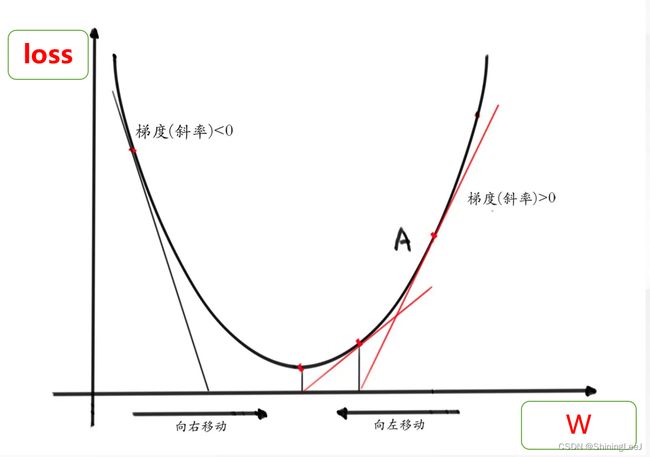
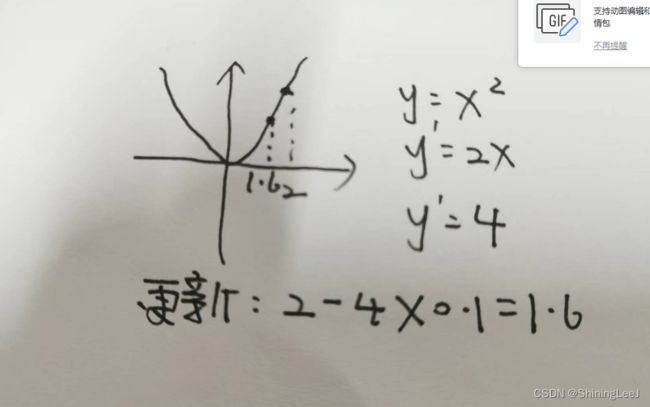
         进行反向传播的目的是将损失降到最低，也就是达到导数为0的点。将简化后的公式进行求导，得到梯度（斜率），将得到的梯度（斜率）乘以一个学习率（比如说为0.1），再去更新参数。

         这里注意学习率不可过大，如果学习率过大会出现直接跳过最低点的情况。这里是一个参数的情况，在存在w，b两个参数的情况下，使用偏导，也就是将一个参数看为常数，对另外一个参数进行求导。

         这里讨论的仅仅是一层的感知机，在真正的全连接神经网络之中是远远不止的。上一层的输出会带入到下一层的输入，所以就需要运用到链式法则来进行求导。

 

这里的每一层都使用sigmoid函数进行激活，每一层的输出如下：

 

对w3的偏导数：

对w2的偏导数： 

 对w1的偏导数：