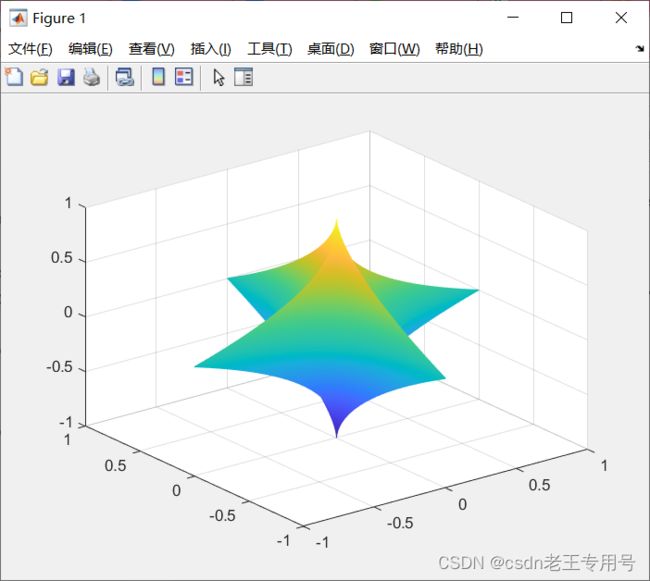
Matlab代码:绘制超二次曲面(超椭球体)
使用Matlab绘制超二次曲面
- 一、超二次曲面解析式与参数方程
- 二、matlab代码与运行结果
一、超二次曲面解析式与参数方程
超二次曲面的统一解析式为如下:
( x − x 0 h 1 ) 2 m + ( y − y 0 h 2 ) 2 n + ( z − z 0 h 3 ) 2 p = 1 \Big(\frac{x-x_0}{h_1}\Big)^{2m}+\Big(\frac{y-y_0}{h_2}\Big)^{2n}+\Big(\frac{z-z_0}{h_3}\Big)^{2p} = 1 (h1x−x0)2m+(h2y−y0)2n+(h3z−z0)2p=1
其中 ( x , y , z ) (x,y,z) (x,y,z) 表示超二次曲面上的任意一点, ( x 0 , y 0 , z 0 ) (x_0,y_0,z_0) (x0,y0,z0) 表示超二次曲面的中心点坐标, h 1 > 0 , h 2 > 0 , h 3 > 0 h_1>0,h_2>0,h_3>0 h1>0,h2>0,h3>0 和 m > 0 , n > 0 , p > 0 m>0,n>0,p>0 m>0,n>0,p>0 分别描述超二次曲面的体积参数和形状参数。
我这里是利用参数方程来对超二次曲面进行绘制
参数方程如下:
x = h 1 ∗ ( s i n ( β ) . ∗ c o s ( α ) ) 1 / m + x 0 y = h 2 ∗ ( s i n ( β ) . ∗ s i n ( α ) ) 1 / n + y 0 z = h 3 ∗ ( c o s ( β ) ) 1 / p + z 0 \begin{aligned} x &= h_1*(sin(\beta).*cos(\alpha))^{1/m}+x_0\\ y &= h_2*(sin(\beta).*sin(\alpha))^{1/n}+y_0\\ z &= h_3*(cos(\beta))^{1/p}+z_0\\ \end{aligned} xyz=h1∗(sin(β).∗cos(α))1/m+x0=h2∗(sin(β).∗sin(α))1/n+y0=h3∗(cos(β))1/p+z0
其中 0 < α < π 0<\alpha<\pi 0<α<π 且 0 < β < 2 π 0<\beta<2\pi 0<β<2π。
二、matlab代码与运行结果
需要注意根据象限进行分类,三维一共8个象限
h1 = 1; h2 = 1; h3 = 1; %曲面体积参数
m = 0.2; n = 0.3; p = 0.5; %曲面形状参数
x0 = 0; y0 = 0; z0 = 0; %超二次曲面中心点坐标
% 参数方程 需要分类解析 共八种情况
part = 1000;
alpha = linspace(0,pi,part); beta = linspace(0,2*pi,part);
for i = 1:1:part
for j = 1:1:part
if (sin(beta(i))*cos(alpha(j))>=0 && sin(beta(i))*sin(alpha(j))>=0 && cos(beta(i))>=0)
x(i,j) = h1*(sin(beta(i)).*cos(alpha(j))).^(1/m)+x0;
y(i,j) = h2*(sin(beta(i)).*sin(alpha(j))).^(1/n)+y0;
z(i,j) = h3*(cos(beta(i))).^(1/p)+z0;
else if (sin(beta(i))*cos(alpha(j))>=0 && sin(beta(i))*sin(alpha(j))>=0 && cos(beta(i))<0)
x(i,j) = h1*(sin(beta(i)).*cos(alpha(j))).^(1/m)+x0;
y(i,j) = h2*(sin(beta(i)).*sin(alpha(j))).^(1/n)+y0;
z(i,j) = -h3*abs(cos(beta(i))).^(1/p)+z0;
else if (sin(beta(i))*cos(alpha(j))>=0 && sin(beta(i))*sin(alpha(j))<0 && cos(beta(i))>=0)
x(i,j) = h1*(sin(beta(i)).*cos(alpha(j))).^(1/m)+x0;
y(i,j) = -h2*abs(sin(beta(i)).*sin(alpha(j))).^(1/n)+y0;
z(i,j) = h3*(cos(beta(i))).^(1/p)+z0;
else if (sin(beta(i))*cos(alpha(j))>=0 && sin(beta(i))*sin(alpha(j))<0 && cos(beta(i))<0)
x(i,j) = h1*(sin(beta(i)).*cos(alpha(j))).^(1/m)+x0;
y(i,j) = -h2*abs(sin(beta(i)).*sin(alpha(j))).^(1/n)+y0;
z(i,j) = -h3*abs(cos(beta(i))).^(1/p)+z0;
else if (sin(beta(i))*cos(alpha(j))<0 && sin(beta(i))*sin(alpha(j))>=0 && cos(beta(i))>=0)
x(i,j) = -h1*abs(sin(beta(i)).*cos(alpha(j))).^(1/m)+x0;
y(i,j) = h2*(sin(beta(i)).*sin(alpha(j))).^(1/n)+y0;
z(i,j) = h3*(cos(beta(i))).^(1/p)+z0;
else if (sin(beta(i))*cos(alpha(j))<0 && sin(beta(i))*sin(alpha(j))>=0 && cos(beta(i))<0)
x(i,j) = -h1*abs(sin(beta(i)).*cos(alpha(j))).^(1/m)+x0;
y(i,j) = h2*(sin(beta(i)).*sin(alpha(j))).^(1/n)+y0;
z(i,j) = -h3*abs(cos(beta(i))).^(1/p)+z0;
else if (sin(beta(i))*cos(alpha(j))<0 && sin(beta(i))*sin(alpha(j))<0 && cos(beta(i))>=0)
x(i,j) = -h1*abs(sin(beta(i)).*cos(alpha(j))).^(1/m)+x0;
y(i,j) = -h2*abs(sin(beta(i)).*sin(alpha(j))).^(1/n)+y0;
z(i,j) = h3*(cos(beta(i))).^(1/p)+z0;
else if (sin(beta(i))*cos(alpha(j))<0 && sin(beta(i))*sin(alpha(j))<0 && cos(beta(i))<0)
x(i,j) = -h1*abs(sin(beta(i)).*cos(alpha(j))).^(1/m)+x0;
y(i,j) = -h2*abs(sin(beta(i)).*sin(alpha(j))).^(1/n)+y0;
z(i,j) = -h3*abs(cos(beta(i))).^(1/p)+z0;
end
end
end
end
end
end
end
end
end
end
figure(1)
mesh(x,y,z); %绘制超二次曲面