卷积神经网络学习心得

卷积神经网络学习心得

---

---

一、卷积神经网络

1、卷积

一、卷积核（算子，即卷积神经网络上的提取特征的滤波窗口）
理解一
在卷积神经网络中，“卷积”更像是一个，特征提取算子。什么是特征提取算子呢？简单来说就是，提取图片纹理、边缘等特征信息的滤波器。
如：

如上图所示，假设，猫的上眼皮部分（框出部分），这部分的数据，展开后如图中数组所示**（这里，为了叙述简便，忽略了rgb三维通道，把图像当成一个二维数组[类比灰度图片]），我们使用一个算子，来检测横向边沿**——这个算子，让第一行的值减去第三行的值，得出结果。具体计算过程如下，比如，原图左上角数据，经过这个算子：
200×1+199×1+189×1+203×0+23×0+34×0+177×(−1)+12×(−1)+22×(−1)=328
然后，算子向右滑动一个像素，得到第二个输出：533，依次向右滑动，最终得到第一行输出；
​然后，向下滑动一个像素，到达第二行；在第二行，从左向右滑动，得到第二行输出……

从输出结果可以看出，在上眼皮处颜色较深，而眼皮上方和下方，无论是眼皮上方的毛发，还是眼皮下方的眼白，颜色都很浅，因此，这样做之后，如果滤波结果中有大值出现，就意味着，这里出现了横向边沿。不断在原图上滑动这个算子，我们就可以，检测到图像中所有的横向边沿。传统的机器视觉方法，就是设计更多更复杂的算子，检测更多的特征，最后，组合这些特征，得出判断结果。
​ 卷积神经网络，做了类似的事情，所谓卷积，就是把一个算子在原图上不断滑动，得出滤波结果——这个结果，我们叫做“特征图”（Feature Map），这些算子被称为“卷积核”(Convolution Kernel)。不同的是，我们不必人工设计这些算子，而是使用随机初始化，来得到很多卷积核（算子），然后通过反向传播，优化这些卷积核，以期望得到更好的识别结果。
理解二
定义一个卷积核（相当于权重），用来从图像中提取一定的特征。卷积核与数字矩阵对应位相乘再相加，得到卷积层输出结果。

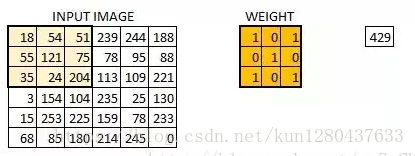
（429 = 181+540+511+550+1211+750+351+240+204*1）
卷积核的取值在没有以往学习的经验下，可由函数随机生成，再逐步训练调整

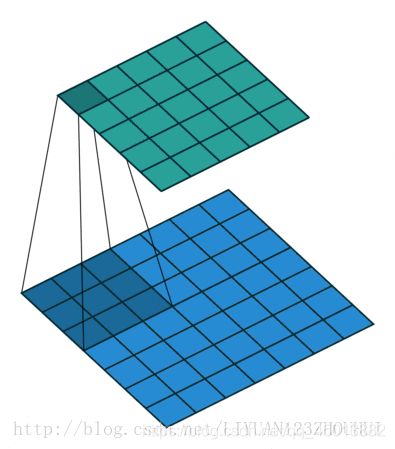
当所有的像素点都至少被覆盖一次后，就可以产生一个卷积层的输出（下图的步长为1）
机器一开始并不知道要识别的部分具有哪些特征，是通过与不同的卷积核相作用得到的输出值，相互比较来判断哪一个卷积核最能表现该图片的特征——比如我们要识别图像中的某种特征（比如曲线），也就是说，这个卷积核要对这种曲线有很高的输出值，对其他形状（比如三角形）则输出较低。卷积层输出值越高，就说明匹配程度越高，越能表现该图片的特征。
卷积层的具体工作过程
比如我们设计的一个卷积核如下左，想要识别出来的曲线如下右：

现在我们用上面的卷积核，来识别这个简化版的图片——一只漫画老鼠

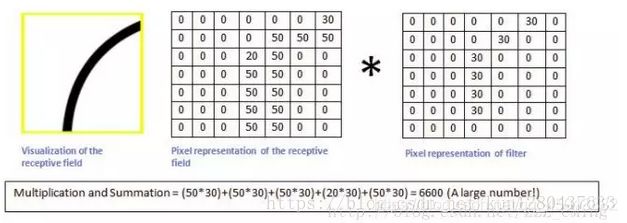
而用同一个卷积核，来识别老鼠的耳朵的时候，输出则很小：0

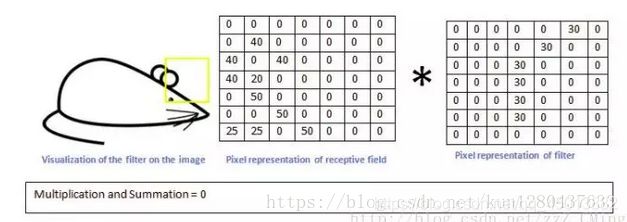
我们就可以认为：现有的这个卷积核保存着曲线的特征，匹配识别出来了老鼠的屁股是曲线的。我们则还需要其他特征的卷积核，来匹配识别出来老鼠的其他部分。卷积层的作用其实就是通过不断的改变卷积核，来确定能初步表征图片特征的有用的卷积核是哪些，再得到与相应的卷积核相乘后的输出矩阵

二、卷积核（算子）的权重
权重共享：在卷积神经网络中，卷积层的每一个卷积滤波器重复的作用于整个感受野中，对输入图像进行卷积，卷积结果构成了输入图像的特征图，提取出图像的局部特征。每一个卷积滤波器共享相同的参数，包括相同的权重矩阵和偏置项。共享权重的好处是在对图像进行特征提取时不用考虑局部特征的位置。而且权重共享提供了一种有效的方式，使要学习的卷积神经网络模型参数数量大大降低。
一个卷积核（相当于权重），用来从图像中提取一定的特征。卷积核与数字矩阵对应位相乘再相加，得到卷积层输出结果。
权重共享的作用：
权重共享 就是一个算子的权重作用于整张图片，主要用于提取某一类事物（具体看理解2）。训练的时候，不断的去训练识别一个物体1，识别该物体1的权重就会训练成具有该类物体的特征（即用该算子扫描其相应的图片时，该图片中的物体1就会与该算子相互作用输出一个特征更强的矩阵，而其他无关的物体与该算子相互作用之后就会削弱其特征，二重点突出该物体1）。权重共享，整张图片都用同一个算子，才会得到重点突出某一个物体的特征，削弱其他物体的特征的效果,所以最终得到的训练结果就是适合的权重，吧这个得到的适合权重，再重新导入到原来的网络中就可以进行对新图片的识别。

2、池化

使用降采样的原因是，根据图像局部相关性的原理，对图像进行子采样可以减少计算量，同时保持图像旋转不变性。
池化层的输入就是卷积层输出的原数据与相应的卷积核相乘后的输出矩阵
最大池化：max-pooling——选取指定区域内最大的一个数来代表整片区域
均值池化：mean-pooling——选取指定区域内数值的平均值来代表整片区域

3、激活函数

分别是s i g m o i d sigmoidsigmoid和r e l u relurelu函数，函数公式如下

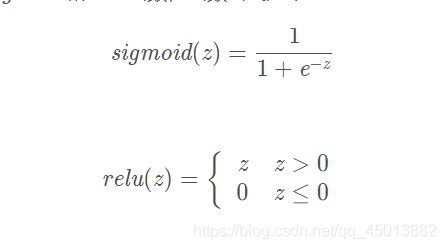
补充说明

引入激活函数的目的是，在模型中引入非线性。如果没有激活函数，那么，无论你的神经网络有多少层，最终都是一个线性映射，单纯的线性映射，无法解决线性不可分问题。引入非线性可以让模型解决线性不可分问题。

一般来说，在神经网络的中间层，更加建议使用r e l u relurelu函数，两个原因：

r e l u relurelu函数计算简单，可以加快模型速度；
由于反向传播过程中，需要计算偏导数，通过求导可以得到，s i g m o i d sigmoidsigmoid函数导数的最大值为0.25，如果使用s i g m o i d sigmoidsigmoid函数的话，每一层的反向传播，都会使梯度最少变为原来的四分之一，当层数比较多的时候可能会造成梯度消失，从而模型无法收敛。

3、全连接层

卷积层和池化层的工作就是提取特征，并减少原始图像带来的参数。然而，为了生成最终的输出，我们需要应用全连接层来生成一个等于我们需要的类的数量的分类器。

全连接层的工作原理和之前的神经网络学习很类似，我们需要把池化层输出的张量重新切割成一些向量，乘上权重矩阵，加上偏置值，然后对其使用ReLU激活函数，用梯度下降法优化参数既可。

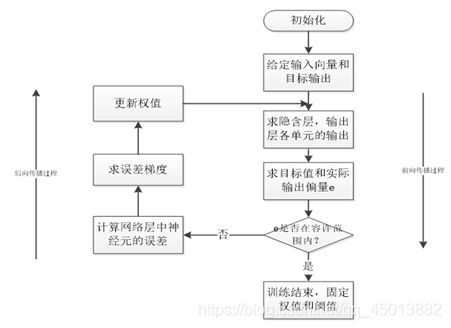
3、训练过程

1、网络进行权值的初始化；

2、输入数据经过卷积层、下采样层、全连接层的向前传播得到输出值；

3、求出网络的输出值与目标值之间的误差；

4、当误差大于我们的期望值时，将误差传回网络中，依次求得全连接层，下采样层，卷积层的误差。各层的误差可以理解为对于网络的总误差，网络应承担多少；当误差等于或小于我们的期望值时，结束训练。

5、根据求得误差进行权值更新。然后在进入到第二步。

二、传播过程

1.卷积神经网络的前向传播过程

1.1卷积层的前向传播过程

卷积层的向前传播过程是，通过卷积核对输入数据进行卷积操作得到卷积操作。数据在实际的网络中的计算过程，我们以图3-4为例，介绍卷积层的向前传播过程。其中一个输入为15个神经元的图片，卷积核为2×2×1的网络，即卷积核的权值为W1，W2，W3，W4。那么卷积核对于输入数据的卷积过程，如下图4-2所示。卷积核采用步长为1的卷积方式，卷积整个输入图片，形成了局部感受野，然后与其进行卷积算法，即权值矩阵与图片的特征值进行加权和（再加上一个偏置量），然后通过激活函数得到输出。

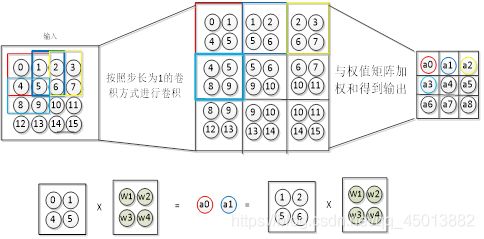
图4-2图片深度为1，卷积层的向前传播过程
而在图3-4中，图片深度为2时，卷积层的向前传播过程如图4-3所示。输入的图片的深度为4×4×2，卷积核为2×2×2，向前传播过程为，求得第一层的数据与卷积核的第一层的权值的加权和，然后再求得第二层的数据与卷积核的第二层的权值的加权和，两层的加权和相加得到网络的输出。

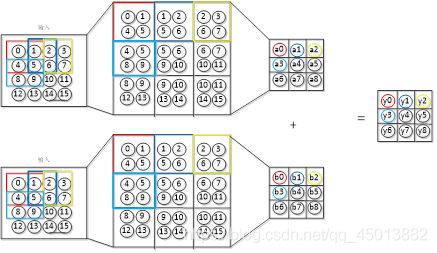
1.2下采样层的前向传播过程

上一层（卷积层）提取的特征作为输入传到下采样层，通过下采样层的池化操作，降低数据的维度，可以避免过拟合。如图4-4中为常见的池化方式示意。最大池化方法也就是选取特征图中的最大值。均值池化则是求出特征图的平均值。随机池化方法则是先求出所有的特征值出现在该特征图中的概率，然后在来随机选取其中的一个概率作为该特征图的特征值，其中概率越大的选择的几率越大。

1.3全连接层的向前传播过程

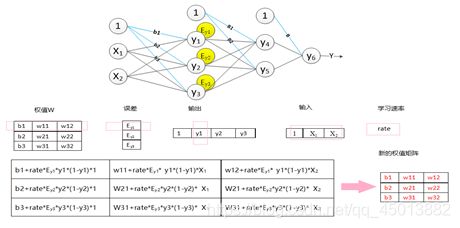
特征图进过卷积层和下采样层的特征提取之后，将提取出来的特征传到全连接层中，通过全连接层，进行分类，获得分类模型，得到最后的结果。图4-5为一个三层的全连接层。假设卷积神经网络中，传入全连接层的特征为x1,x2。则其在全连接层中的向前传播过程如图4-5所示。第一层全连接层有3个神经元y1,y2,y3。这三个节点的权值矩阵为W，其中b1,b2,b3分别为节点y1,y2,y3的偏置量。可以看出，在全连接层中，参数的个数=全连接层中节点的个数×输入的特征的个数+节点的个数（偏置量）。其向前传递过程具体如图所示，得到输出矩阵后，经过激励函数f(y)的激活，传入下一层。

2.全连接层的向前传播过程

当卷积神经网络输出的结果与我们的期望值不相符时，则进行反向传播过程。求出结果与期望值的误差，再将误差一层一层的返回，计算出每一层的误差，然后进行权值更新。该过程的主要目的是通过训练样本和期望值来调整网络权值。误差的传递过程可以这样来理解，首先，数据从输入层到输出层，期间经过了卷积层，下采样层，全连接层，而数据在各层之间传递的过程中难免会造成数据的损失，则也就导致了误差的产生。而每一层造成的误差值是不一样的，所以当我们求出网络的总误差之后，需要将误差传入网络中，求得该各层对于总的误差应该承担多少比重。

反向传播的训练过程的第一步为计算出网络总的误差：求出输出层n的输出a(n)与目标值y之间为误差。计算公式为：

其中，为激励函数的导函数的值。

2.1全连接层之间的误差传递

求出网络的总差之后，进行反向传播过程，将误差传入输出层的上一层全连接层，求出在该层中，产生了多少误差。而网络的误差又是由组成该网络的神经元所造成的，所以我们要求出每个神经元在网络中的误差。求上一层的误差，需要找出上一层中哪些节点与该输出层连接，然后用误差乘以节点的权值，求得每个节点的误差,具体如图所示：

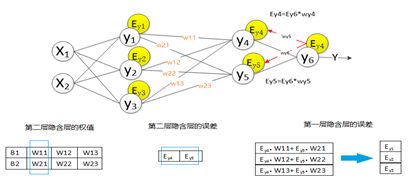
图4-6 全连接层中误差的传递过程

2.2当前层为下采样层，求上一层的误差

在下采样层中，根据采用的池化方法，把误差传入到上一层。下采样层如果采用的是最大池化（max-pooling）的方法，则直接把误差传到上一层连接的节点中。果采用的是均值池化（mean pooling）的方法，误差则是均匀的分布到上一层的网络中。另外在下采样层中，是不需要进行权值更新的，只需要正确的传递所有的误差到上一层。

2.3当前层为卷积层，求上一层的误差

卷积层中采用的是局部连接的方式，和全连接层的误差传递方式不同，在卷积层中，误差的传递也是依靠卷积核进行传递的。在误差传递的过程，我们需要通过卷积核找到卷积层和上一层的连接节点。求卷积层的上一层的误差的过程为：先对卷积层误差进行一层全零填充，然后将卷积层进行一百八十度旋转，再用旋转后的卷积核卷积填充过程的误差矩阵，并得到了上一层的误差。如图4-7为卷积层的误差传递过程。图右上方为卷积层的向前卷积过程，而右下方为卷积层的误差传递过程。从图中可以看出，误差的卷积过程正好是沿着向前传播的过程，将误差传到了上一层。

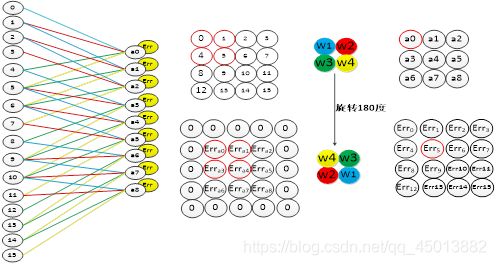
图4-7卷积层的误差传递过程

3卷积神经网络的权值更新

3.1卷积层的权值更新

卷积层的误差更新过程为：将误差矩阵当做卷积核，卷积输入的特征图，并得到了权值的偏差矩阵，然后与原先的卷积核的权值相加，并得到了更新后的卷积核。如图4-8，图中可以看出，该卷积方式的权值连接正好和向前传播中权值的连接是一致的。

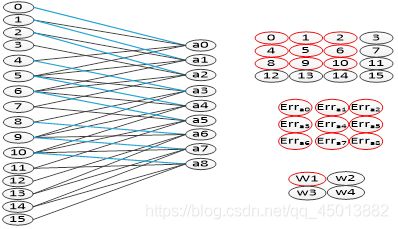
图4-8卷积核的权值更新过程

3.2全连接层的权值更新过程

全连接层中的权值更新过程为：

1、求出权值的偏导数值：学习速率乘以激励函数的倒数乘以输入值；

2、原先的权值加上偏导值，得到新的权值矩阵。具体的过程如图4-9所示（图中的激活函数为Sigmoid函数）。

总结