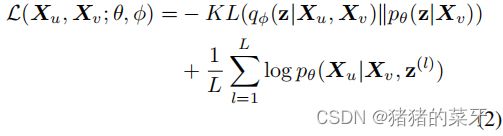Local Augmentation for Graph Neural Networks

目录

1 内容简介

2 主要贡献

3 准备工作

4 LA-GNN

4.1局部增强-LA

4.1.1动机

4.1.2效果

4.1.3方法

4.1.4讨论

4.2从下游图学习的生成模型训练

4.3 损失函数 

4.3.1 监督损失

4.3.2 一致性正则化损失

5 训练和推理过程

6 总结

1 内容简介

GNN 的关键思想是通过聚合来自本地邻域的信息来获得信息表示。

然而，邻域信息是否被充分聚合以学习具有少数邻居的节点的表示仍然是一个悬而未决的问题。

为了解决这个问题，本文提出了一种简单有效的数据增强策略，即局部增强，以学习以中心节点表示为条件的邻居节点表示的分布，并通过生成的特征增强 GNN 的表达能力。

局部增强是一个通用框架，可以以即插即用的方式应用于任何 GNN 模型。

它从学习的条件分布中对与每个节点相关联的特征向量进行采样，作为每次训练迭代中主干模型的附加输入。

GNN的核心是使用一种消息传递机制，从本地邻居中传递和聚合信息，以生成信息表示。

尽管GNN在从局部邻域学习节点表示方面取得了进展，但局部邻域信息是否足以获得有效的节点表示，特别是对于邻居数量有限的节点，仍然是一个开放的问题。

作者认为，局部邻域中有限数量的邻居限制了GNN的表达能力，阻碍了它们的性能，特别是在一些节点的邻居很少的样本匮乏情况下。

堆叠图层以扩大接受域可以合并多跳相邻信息，但会导致过度平滑，而没有与输入的剩余连接，并不是解决这个问题的直接解决方案。

现有的GNN模型架构的工作不能解决非常有限的邻居不利于学习节点表示的问题。

因此，重点是丰富低度节点的局部信息，以获得有效的表示。

为了促进在本地邻域中生成更多样本的聚合方案，本文提出了一种新颖高效的数据增强框架：图神经网络的局部增强 Local Augmentation GNN(LA-GNN)。

“局部增强”是指通过以局部结构和节点特征为条件的生成模型生成邻域特征。

具体来说，本文提出的框架包括一个预训练步骤，该步骤通过生成模型学习给定一个中心节点特征的连接邻居节点特征的条件分布。

如下图所示，然后利用该分布生成与该中心节点相关的特征向量，作为每次训练迭代的附加输入。此外，将生成模型的预训练和下游 GNN 训练解耦，允许数据增强模型以即插即用的方式应用于任何 GNN 模型。

图上的黄色圆圈对应于邻居节点。假设我们已经了解了局部邻域的分布，我们从局部邻域分布中生成特征，然后我们将原始特征和生成的特征作为下游GNN的输入。

2 主要贡献

• 提出了一种通用的增强策略，以在局部邻域中生成更多特征，以增强现有 GNN 的表达能力；

• 探索了图的预训练生成模型的新方向，以提高下游任务性能；

• 提出的框架是灵活的，可以应用于各种流行的骨干网。

3 准备工作

设G=(V,E)表示图，V节点集，E边集，即共有N个节点。

邻接矩阵定义为，即i、j 两点之间有边相连则，否则为0。

表示节点 的邻域，D表示度矩阵。

X表示特征矩阵，每一个节点v 都有一个特征向量与之相关联。

许多流行的GNNs直接对图结构进行操作，并通过图节点之间的消息传递来捕获图的依赖性。反复聚合节点v的邻域 的表示，并将聚合的信息及其表示向量组合起来，得到一个表示向量。GNN消息传递方案的第k层节点v 的表示向量是：

其中COM（·）和AGG（·）分别表示组合函数和聚合函数，为节点u和节点v之间的边向量。。

式(1)表示：节点v的所有第k-1层的邻居节点u的向量表示与所有相邻边二者的信息通过AGG(·)函数进行聚合 ，聚合后再与第k-1层的节点v的向量表示通过COM(·)函数进行信息的组合，得到第k层节点v 的表示向量。

以上便是GNN消息传递方案通过信息的聚合来更新节点的表示向量的过程。

4 LA-GNN

4.1局部增强-LA

4.1.1提出原因

现有的 GNN 专注于设计一种消息传递方案，以利用局部信息来获取节点表示。本文探索了一个新的方向，即可以在局部邻域中生成更多样本，特别是对于具有较少邻居的节点，以增强各种 GNN 的表达能力。为了在节点v 的邻域 中产生更多样本，需要知道其邻居节点表示的分布。由于这个分布与中心节点v 有关，可以通过生成模型根据中心节点的表示来学习它。

4.1.2效果

与为每个节点训练生成模型相比，为所有节点训练单个生成模型有三个好处：

1）通过生成模型学习图上所有节点的条件分布降低了计算成本。

2）在生成阶段，可以应用特定节点的特征向量作为输入(条件)并生成与该节点相关的特征向量。

3）具有更好的可扩展性和泛化性。对于添加到动态图中的新节点，可以直接生成特征向量，而无需重新训练新的生成模型，因为生成模型包含这样的泛化信息。

所以局部增强模型可以应用于归纳学习任务，例如图分类。

4.1.3方法

作者利用条件变分自动编码器conditional variational auto encoder (CVAE) 来学习给定中心节点 的连接邻居 的节点特征的条件分布。关于CVAE的设置，作者使用作为条件，因为的分布与有关。潜在变量 是从prior distribution---先验分布生成的，数据是通过以和 为条件的生成分布生成的：，。

令 表示变分参数， 表示生成参数，存在如下关系：

KL散度为不小于0的距离度量。

具体过程：

 并且证据下界（ELBO）可以写成：

式中 ，，L为节点v 的邻居数。

具体过程：

 正如前面讨论的，只是为所有节点训练一个CVAE。在训练阶段，目标是使用相邻的对作为输入，以最大化式 (2)的ELBO。在生成阶段，我们使用节点特征作为条件，并采样一个潜在变量作为解码器的输入。然后得到与节点v 相关联的生成特征向量。

4.1.4讨论

在学习以中心节点为条件的邻居特征的分布时，我们不考虑连接到每个邻居的其他节点对邻居特征的影响。该假设避免了对多跳邻居的条件作用的指数复杂度，显著提高了可伸缩性。

CVAE的具体过程如下：

作者基于MLP构建了CVAE。编码器和解码器都是两层MLP，每层有256个隐藏单元。对于节点 及其邻域，在训练阶段提取相邻节点对作为CVAE的输入，其中u∈Nv。在推理阶段，从中提取的一个潜在变量 和中心节点 的特征向量作为CVAE解码器的输入。因此，可以得到生成的特征向量。 

4.2从下游图学习的生成模型训练

大多数现有的GNN模型遵循消息传递机制，可以视为一个学习的分类或回归函数。为了进行预测，GNN模型需要估计相对于图结构 A 和特征矩阵 X 的后验分布PΘ(·|A，X)。如 · 可以是节点分类任务上的类标签Y。我们可以使用最大似然估计(MLE)，通过优化以下似然函数来估计参数Θ：

其中，i表示训练数据集中的第i个数据点。

 在我们的局部增强模型中，为了进一步提高GNN的表达能力，利用 作为输入条件，为中心节点v引入一个生成的特征向量，并从生成模型中进行采样。表示第 j 行生成的特征向量。在等式（3）中加入重写得到：

为了实现贝叶斯的可处理性，把等式（4）中的分解为两个后验概率的乘积：

其中，和分别表示GNN模型和生成模型近似的概率分布，由和参数化。

通过这样做，我们可以解耦提出的局部增强和特定的图学习，允许我们的增强模型应用于各种GNN模型，只对生成模型进行一次预训练。因此，局部增强可以看作是GNN训练之前的无监督预训练模型。等式（5）的表示能力优于单一预测器，因为我们为GNN模型提供了更多的局部邻居生成的样本。

4.3 损失函数 

训练LAGNNs的两个损失函数：监督损失和一致性损失。

4.3.1 监督损失

一旦完成了局部增强模型的预训练，我们就使用它生成的特征矩阵作为额外的输入，以增强GNN模型的表达能力。给定训练标签 K 和 S 增广特征矩阵，我们可以将节点分类任务的监督损失函数写成如下：

其中，。这只提供了一种监督损失函数，对于其他的图学习任务，如链接预测和图分类，监督损失函数可以进行相应的调整。 

4.3.2 一致性正则化损失

具体来说，一致性正则化损失函数的形式如下：

其中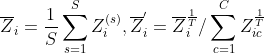，是锐化技巧，T是一个超参数，它可以调整这个分类分布的“温度”。锐化技巧可以减少预测的熵。 

5 训练和推理过程

首先，训练 CVAE，即局部增强模型。然后在每次训练迭代中采样一个由 CVAE 生成的不同特征矩阵作为附加输入来训练 GNN 模型。但是对于 GRAND，作者只在训练阶段对一个特征矩阵进行采样，因为作者研究发现使用这种采样策略可以获得更好的性能。

6 总结

本文提出了局部增强，这是一种利用生成模型来学习给定中心节点特征的中心节点邻居特征的条件分布的新技术。作者将生成的特征矩阵从训练有素的生成模型馈送到一些修改过的主干 GNN 模型，以提高它们的性能。实验表明，本文模型可以提高各种 GNN 架构和基准数据集的性能。此外，本文模型在各种半监督节点分类任务上取得了新的最先进的结果。本文提出的框架的一个限制是不利用 2 跳邻居或使用随机游走来为中心节点找到更多相关的邻居。未来的一项工作是如果中心节点的度数较小，则提取更多的 2或3 跳邻居，如果图较大，则学习随机采样节点的条件分布。