模式识别 K-mean|KNN

模式识别 K-mean|KNN

本篇文章以题目与题解的角度对K-mean与KNN进行简单介绍，所用题目为课程结业时的课题。作者是个小白，若文中存在错误之处，望批评指正！

模式识别——课题

有两个类别，x，y，样本的分布规律服从正态分布，其均值和方差分别为（2，2），（－2，4），每个类别里面分别有样本100个，按题目要求实现：
1.用k-mean对两类样本聚类
2.在（1）的基础上请使用k-近邻法判断下列sample中样本的分类情况（-0.7303，2.1624），（1.4445，-0.1649），（-1.2587，0.9187），（1.2617，-0.2086），（0.7302，1.6587）
3.讨论K值对分类的影响

注：数据链接

数据X_Ydata与label_XY
https://pan.baidu.com/s/1bA3-9KLQmJQuoYlq55Bg3A?pwd=qqrt%20%20提取码：qqrt

K-mean算法

条件

1、待分类的数据集
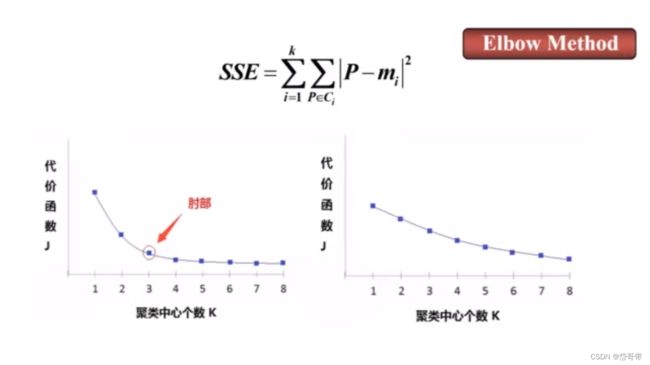
2、人工取定分类数目K（先验知识）或利用肘部法则确定K

K值的两种确定方法

基本思想

该方法取定 K个类别和选取K个初始聚类中心，按最小距离原则将各模式分配到 K类中的某一类，之后不断地计算类心和调整各模式的类别，最终使各模式到其判属类别中心的距离平方之和最小。

局限性

对数据分布敏感；对异常数据敏感；K的取值不容易确定

例题

已知有20个样本，每个样本有2个特征，数据分布如下图,使用K－均值法实现样本分类（K=2）。

样本序号	X1	X2	X3	X4	X5	X6	X7	X8	X9	X10	X11	X12	X13	X14	X15	X16	X17	X18	X19	X20
特征X1	0	1	0	1	2	1	2	3	6	7	8	6	7	8	9	7	8	9	8	9
特征X2	0	0	1	1	1	2	2	2	6	6	6	7	7	7	7	8	8	8	9	9

以X1，X2为坐标轴可得下图

第一步，令K=2，选初始聚类中心为

第二步，计算最小距离

||X-Y||表示向量的二范式，也可以称为欧氏距离，计算方法可用两点间的距离公式

得出分类图

第三步，根据新分成的两类，建立新的聚类中心

重复步骤2，得到新的两个分类后，再计算新的聚类中心

分类图

课题第一问

有两个类别，x，y，样本的分布规律服从正态分布，其均值和方差分别为（2，2），（－2，4），每个类别里面分别有样本100个，按题目要求实现：
1.用k-mean对两类样本聚类
根据上述对K-mean算法的介绍，利用matlab得到如下程序：
（K值这里是人工确定，没有利用肘部法则）

注：数据预处理，利用MATLAB的导入数据功能，将Excel的数据转存为mat文件。

clear all;close all;clc;
%数据处理
x1=cell2mat(struct2cell(load('X_Ydata.mat','x1')));%将结构体类型转换为矩阵
x2=cell2mat(struct2cell(load('X_Ydata.mat','x2')));%将结构体类型转换为矩阵
y1=cell2mat(struct2cell(load('X_Ydata.mat','y1')));%将结构体类型转换为矩阵
y2=cell2mat(struct2cell(load('X_Ydata.mat','y2')));%将结构体类型转换为矩阵
X=[x1 x2];%X数据集
Y=[y1 y2];%Y数据集
data=[X;Y];%X、Y合并后的数据集
N=2;%设置聚类数目
[m,n]=size(data);
pattern=zeros(m,n+1);
center=zeros(N,n);%初始化聚类中心
pattern(:,1:n)=data(:,:);
for x=1:N
    center(x,:)=data( randi(100,1),:);%第一次随机产生聚类中心
end
while 1
distence=zeros(1,N);
num=zeros(1,N);
new_center=zeros(N,n);

for x=1:m
    for y=1:N
    distence(y)=norm(data(x,:)-center(y,:));%计算到每个类的距离
    end
    [~, temp]=min(distence);%求最小的距离
    pattern(x,n+1)=temp;         
end
k=0;
for y=1:N
    for x=1:m
        if pattern(x,n+1)==y
           new_center(y,:)=new_center(y,:)+pattern(x,1:n);
           num(y)=num(y)+1;
        end
    end
    new_center(y,:)=new_center(y,:)/num(y);
    if norm(new_center(y,:)-center(y,:))<0.1
        k=k+1;
    end
end
if k==N
     break;
else
    center=new_center;
end
end
[m, n]=size(pattern);
%最后显示聚类后的数据
figure;
hold on;
for i=1:m
    if pattern(i,n)==1 
         plot(pattern(i,1),pattern(i,2),'r*');
         plot(center(1,1),center(1,2),'kx', 'MarkerSize', 14,'LineWidth', 4);
    elseif pattern(i,n)==2
         plot(pattern(i,1),pattern(i,2),'g*');
         plot(center(2,1),center(2,2),'kx', 'MarkerSize', 14,'LineWidth', 4);
    elseif pattern(i,n)==3
         plot(pattern(i,1),pattern(i,2),'b*');
         plot(center(3,1),center(3,2),'kx', 'MarkerSize', 14,'LineWidth', 4);
    elseif pattern(i,n)==4
         plot(pattern(i,1),pattern(i,2),'y*');
         plot(center(4,1),center(4,2),'kx', 'MarkerSize', 14,'LineWidth', 4);
    else
         plot(pattern(i,1),pattern(i,2),'m*');
         plot(center(4,1),center(4,2),'kx', 'MarkerSize', 14,'LineWidth', 4);
    end
end
grid on;

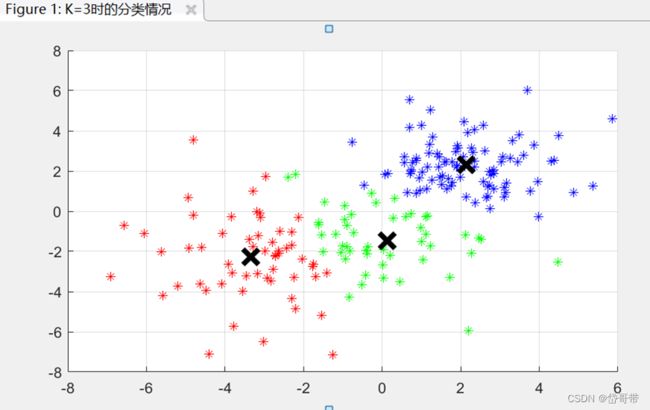
以X为数据集 K=2时，类中心：[1.827,1.341;2.438,3.495]

以X为数据集K=3时，类中心：[2.378,3.888;1.017,1.664;3.148,1.4163]

以X为数据集K=4时，类中心：[3.899,3.384;3.057,1.1008;0.908,1.257;1.598,3.271]

XY合集的分类情况

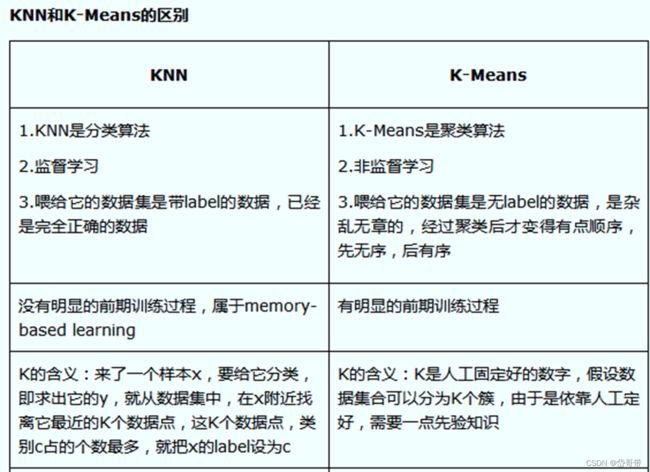
KNN算法

条件

已打上标签的数据集，对输入的待分类数据进行分类。
K值：根据样本的分布，选择一个较小的值，可以通过交叉验证选择一个合适的K值。K代表数据点个数。

基本思想

该方法取定 K个实例，计算离待分类数据距离最近的K个已分类数据的类别，把待分类数据归为类别占据数目最多的那一类。类似于投票表决。

局限性

1.计算成本很高，当数据集是几十亿个样本时，计算量是不可接受的；
2.在训练集较小时，泛化能力很差，非常容易陷入过拟合；
3.无法判断特征的重要性。

课题第二问

有两个类别，x，y，样本的分布规律服从正态分布，其均值和方差分别为（2，2），（－2，4），每个类别里面分别有样本100个，按题目要求实现：
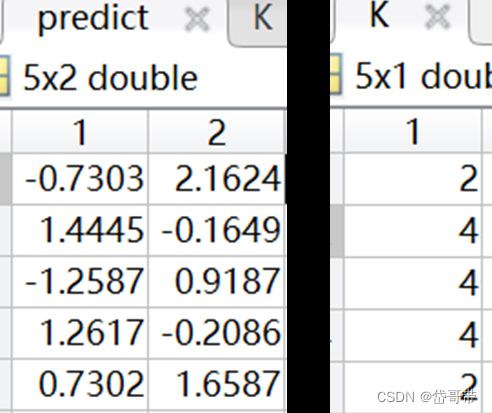
2.在（1）的基础上请使用k-近邻法判断下列sample中样本的分类情况（-0.7303，2.1624），（1.4445，-0.1649），（-1.2587，0.9187），（1.2617，-0.2086），（0.7302，1.6587）。

MATLAB代码

%加载数据集
train_x=xlsread('C:\Users\xiaocong\Desktop\label_XY','A2:A201');
train_y=xlsread('C:\Users\xiaocong\Desktop\label_XY','B2:B201');
k=xlsread('C:\Users\xiaocong\Desktop\label_XY','C2:C201');
predict_x=xlsread('C:\Users\xiaocong\Desktop\label_XY','A202:A206');
predict_y=xlsread('C:\Users\xiaocong\Desktop\label_XY','B202:B206');

%数据分组
train=[train_x train_y];
predict=[predict_x predict_y];
% rowrank=randperm(size(train,1));
% train_data=train(rowrank,:);

%KNN算法
K=knnclassify(predict,train,k,20,'euclidean','random');

结果

说明：K是五个样本点的类别

总结