RoadMap: A Light-Weight Semantic Map for Visual Localization towards Autonomous Driving
华为 秦通
本文贡献：
- 提出了一种用于自动驾驶的轻量化定位框架，包括车端建图，云端维护、融合、压缩，以及用户端定位。
- 使用传感器丰富的地图采集车或者robotaxi来收集更新地图，使用户车收益
- 实车验证所提出方案的有效性
一、车端建图
语义分割
使用语义分割网络获得当前图像中的语义分割结果，然后根据优化的相机位姿将其投影到世界坐标系中。
本文从使用的是基于CNN的语义分割网络（应该是区别于transformer），类似于以下几个网络：
分割类别：ground, lane line, stop line, road marker, curb（路牙）, vehicle, bike, and human，
其中 ground, lane line, stop line, and road marker are used for semantic mapping.其他类别被用于其他自动驾驶任务
反向投影变换 Inverse Perspective Mapping (IPM)
根据图像的消影点实现逆投影变换，但是由于感知噪声，场景距离越远，误差越大，所以本文只考虑ROI之内的像素进行变换（上图红框之内）。投影变换公式：
1 λ [ x v y v 1 ] = [ R c t c ] c o l : 1 , 2 , 4 − 1 π c − 1 ( [ u v 1 ] ) \frac{1}{\lambda}\left[\begin{array}{c} x^{v} \\ y^{v} \\ 1 \end{array}\right]=\left[\begin{array}{ll} \mathbf{R}_{c} \mathbf{t}_{c} \end{array}\right]_{c o l: 1,2,4}^{-1} \pi_{c}^{-1}\left(\left[\begin{array}{l} u \\ v \\ 1 \end{array}\right]\right) λ1⎣⎡xvyv1⎦⎤=[Rctc]col:1,2,4−1πc−1⎝⎛⎣⎡uv1⎦⎤⎠⎞
其中函数 π − 1 \pi^{-1} π−1是主要的逆投影变换，Rc, Tc是相机到车辆坐标系中心的外参
位姿图优化
采用GNSS + 局部里程计的方法优化位姿。
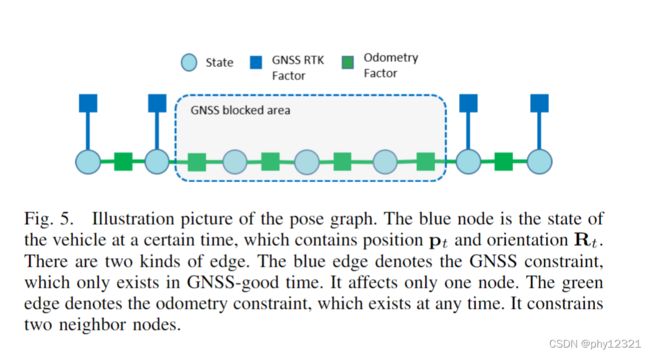
在GNSS信号好的地方最小化与GNSS信号的距离，在GNSS信号不好的地方最小化与里程计的距离：
min s 0 … s n { ∑ i ∈ [ 1 , n ] ∥ r o ( s i − 1 , s i , m ^ i − 1 , i o ) ∥ σ 2 + ∑ i ∈ G ∥ r g ( s i , m ^ i g ) ∥ σ 2 } , \min _{\mathbf{s}_{0} \ldots \mathbf{s}_{n}}\left\{\sum_{i \in[1, n]}\left\|\mathbf{r}_{o}\left(\mathbf{s}_{i-1}, \mathbf{s}_{i}, \hat{\mathbf{m}}_{i-1, i}^{o}\right)\right\|_{\sigma}^{2}+\sum_{i \in \mathcal{G}}\left\|\mathbf{r}_{g}\left(\mathbf{s}_{\mathbf{i}}, \hat{\mathbf{m}}_{i}^{g}\right)\right\|_{\boldsymbol{\sigma}}^{2}\right\}, s0…snmin⎩⎨⎧i∈[1,n]∑∥∥ro(si−1,si,m^i−1,io)∥∥σ2+i∈G∑∥rg(si,m^ig)∥σ2⎭⎬⎫,
r o ( s i − 1 , s i , m ^ i − 1 , i o ) = [ R ( q i − 1 ) − 1 ( p i − p i − 1 ) − δ p ^ i − 1 , i o [ q i − 1 ⋅ q i − 1 ⋅ δ q ^ i − 1 , i o ] x y z ] , r g ( s i , m ^ i g ) = p i − m ^ i g \begin{aligned} \mathbf{r}_{o}\left(\mathbf{s}_{i-1}, \mathbf{s}_{i}, \hat{\mathbf{m}}_{i-1, i}^{o}\right) &=\left[\begin{array}{c} \mathbf{R}\left(\mathbf{q}_{i-1}\right)^{-1}\left(\mathbf{p}_{i}-\mathbf{p}_{i-1}\right)-\delta \hat{\mathbf{p}}_{i-1, i}^{o} \\ {\left[\mathbf{q}_{i}{ }^{-1} \cdot \mathbf{q}_{i-1} \cdot \delta \hat{\mathbf{q}}_{i-1, i}^{o}\right]_{x y z}} \end{array}\right], \\ \mathbf{r}_{g}\left(\mathbf{s}_{\mathbf{i}}, \hat{\mathbf{m}}_{i}^{g}\right) &=\mathbf{p}_{i}-\hat{\mathbf{m}}_{i}^{g} \end{aligned} ro(si−1,si,m^i−1,io)rg(si,m^ig)=[R(qi−1)−1(pi−pi−1)−δp^i−1,io[qi−1⋅qi−1⋅δq^i−1,io]xyz],=pi−m^ig
位姿态图优化的结果：
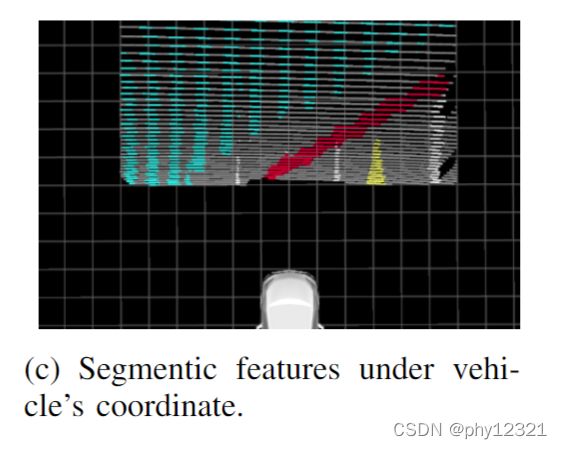
有了相机的pose， 就可以将提取的语义信息从车辆坐标系变换到世界坐标系中：
[ x w y w z w ] = R ( q i ) [ x v y v 0 ] + p i \left[\begin{array}{l} x^{w} \\ y^{w} \\ z^{w} \end{array}\right]=\mathbf{R}\left(\mathbf{q}_{i}\right)\left[\begin{array}{c} x^{v} \\ y^{v} \\ 0 \end{array}\right]+\mathbf{p}_{i} ⎣⎡xwywzw⎦⎤=R(qi)⎣⎡xvyv0⎦⎤+pi
为了防止同一个像素点在不同的帧中被分割成不同的类别，将地图分为0.10.10.1的网格地图，每个网格中保存了位置、语义标签以及标签的count，当一个语义点被分配到网格中时，对应的语义标签计数加一，最后选择最多的一个语义标签作为该网格的语义。去除了语义噪声后的语义地图如下：
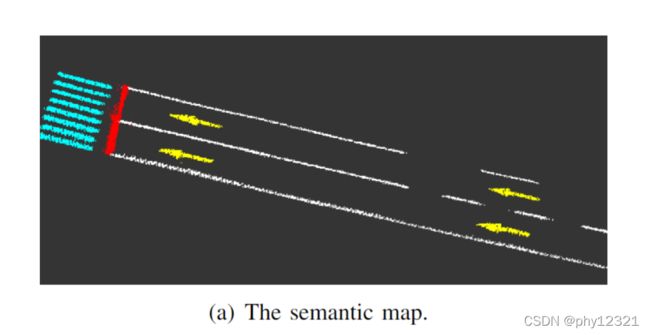
二、云端建图
地图的融合、更新
云端地图也是同样的网格格式，将车端的采集的数据上传到云端后，对每个网格内的语义计数进行即可
为了节省带宽，只上传有占用信息的网格的数据。
地图的压缩
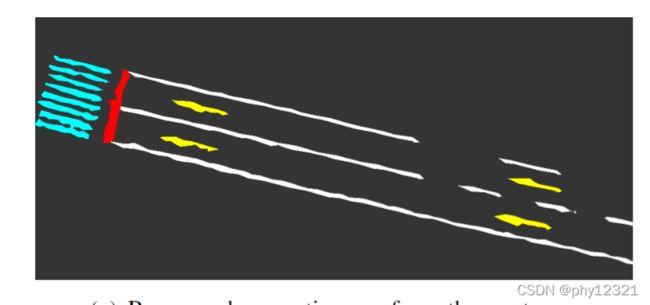
对语义网格进行轮廓提取，然后将轮廓线作为压缩后的地图进行存储。相当于丢弃了轮廓线内部的语义标签和计数信息。
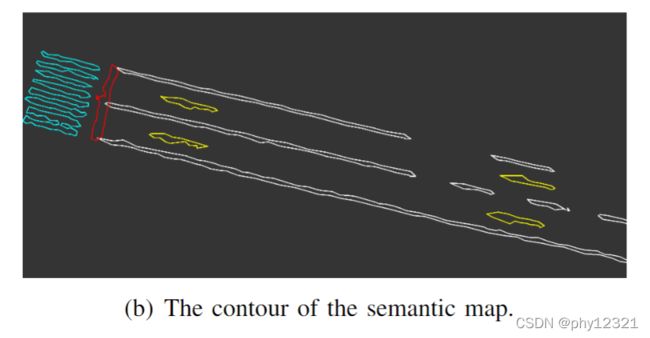
三、用户端定位
地图解压：
使用相同的语义标签填充轮廓线内部的网格：
地图ICP定位
车端进行语义分割，以及逆透视投影，与地图中的语义特征进行ICP配准：
定位过程：
q ∗ , p ∗ = arg min q , p ∑ k ∈ S ∥ R ( q ) [ x k v y k v 0 ] + p − [ x k w y k w z k w ] ∥ 2 , \mathbf{q}^{*}, \mathbf{p}^{*}=\underset{\mathbf{q}, \mathbf{p}}{\arg \min } \sum_{k \in \mathcal{S}}\left\|\mathbf{R}(\mathbf{q})\left[\begin{array}{c} x_{k}^{v} \\ y_{k}^{v} \\ 0 \end{array}\right]+\mathbf{p}-\left[\begin{array}{c} x_{k}^{w} \\ y_{k}^{w} \\ z_{k}^{w} \end{array}\right]\right\|^{2}, q∗,p∗=q,pargmink∈S∑∥∥∥∥∥∥R(q)⎣⎡xkvykv0⎦⎤+p−⎣⎡xkwykwzkw⎦⎤∥∥∥∥∥∥2,
然后使用EKF框架对定位结果进行平滑
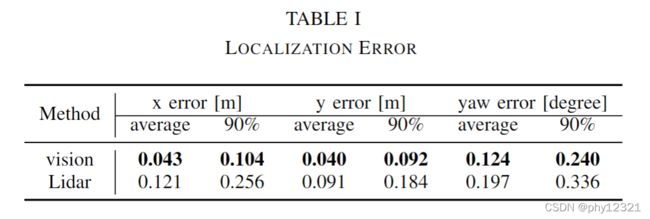
四、实验结果：
多辆采集车联合构建地图：
22KM， 16.7M，压缩后0.786M，平均36KB/KM
与激光雷达定位结果的比较
具体使用激光里程计还是基于激光地图的定位，没有交代。