leetcode 左程云笔记
P2 认识复杂度和简单排序算法
24:12 选择排序
26:53 冒泡排序
33:00 亦或运算可以理解为无进位相加,0亦或A 等于 A ,A亦或A等于0,36:00 不适用额外变量交换两个数
43:00 有关使用亦或的题目,在一个数组中,已知只有一种数出现了奇数次,其他所有数都出现了偶数次,找到这个数。第2问,如果有两种数出现了奇数次,其余都出现了偶数次,找到这两种数
1:07:53 提取出一个数字二进制最右侧的1
1:13 插入排序 先做到0到0位置有序,后做到0到1位置有序,后做到0到2有序,后做到0到3有序。每次都从后往前看,后面的数逐步往前换
插入排序的时间复杂度会因为数据状况的不同而变化,从0(N)到o(N2)。
1:31 在一个有序数组中,找某一个数是否存在
二分法,时间复杂度LogN,因为是一次砍一半
1:37 在一个有序数组中,找到大于等于某个数最左侧的位置
二分法二分到区间内没有数字,找到了这个数字就让right = mid-1
12233344555,找大于等于3最左侧的位置红色的3,首先二分 12233344555,然后黄3满足大于等于3,但是黄三的左侧还可能存在大于等于3的更左的位置(把当前黄三的位置记录下来),所以在黄三的左侧二分12233,然后蓝2不满足大于等于3,在蓝2的右侧二分,33,mid来到红三的位置,满足大于等于3,且比之前黄3的位置更左,就更新这个最左,然后去红三的左边找,没有了,while循环结束。
1:42 局部最小值问题,一个无序数组,任何两个相邻的数不相等
二分法的策略,二分法的标准是因题而异的
1:54 对数器
———————————————————————————————————————————
P3 OnlogN排序
剖析递归行为和时间复杂度的计算
5:00 使用代码结果求数组重点可能发生的溢出问题
9:00 递归结构过程讲解
17:00 master 公式来求解递归问题的时间复杂度
30:00 master公式如何求解时间复杂度
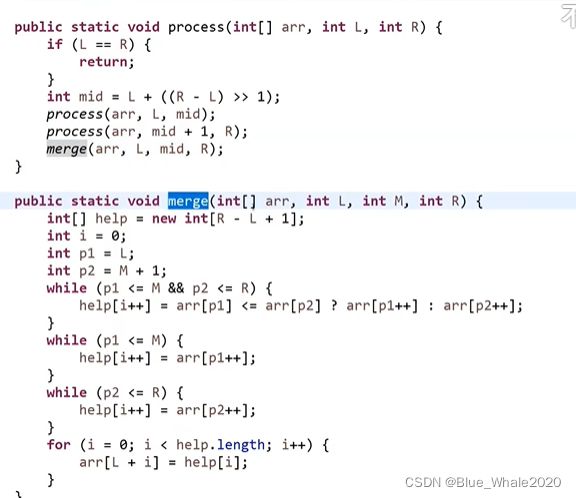
34:00 归并排序 merge sort
先让左侧部分排好序,再让右侧部分排好序,然后整体merge在一起
在递归中实现merge sort
56:00 之前的n平方排序算法为什么差,因为浪费了大量的比较行为没有被记录下来
1:00 小和问题
改写归并排序的merge过程
1:29 归并排序的拓展 逆序对问题,只要右边的数字比左边的数字小,就构成一个逆序对,打印所有逆序对的数量
这种由mergesort改写的题目 ,每年必出
1:31 堆排序
1:40 快速排序和荷兰国旗问题
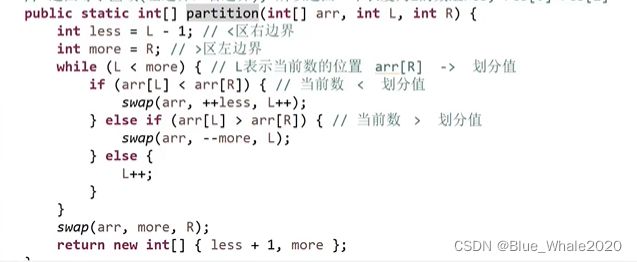
给定一个数,小于等于这个数的都在这个数的左边,大于等于这个数的都在这个数的右边(左边和右边不必有序)
方法:
当前数小于number,把当前数和小于等于区域的下一个数做交换,小于等于区域右扩,当前数也跳转到下一个
当前数i等于number ,直接跳下一个
当前数i大于number,把当前数和大于等于区域的前一个做交换,大于等于左扩,i原地不动
在大于区域和i相等是,过程停止。
2:02 快速排序1.0版本,利用荷兰国旗问题
2:06 快速排序2.0版本,整个区域,把整个数组中的最后一直值作为划分值,小于等于num放左边,等于num放中间,大于num放右边。然后在小于num区域和大于num区域递归,不断的玩下去
快速排序1.0和2.0版本最差的时间复杂度都是o(N2)
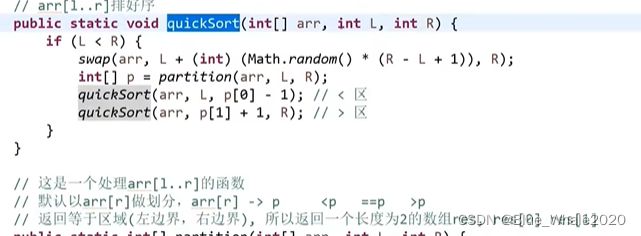
2:14 快速排序3.0 改进可能出现偏差的划分值,随即选择一个划分值
partition返回等于区域的左边界和右边界
———————————————————————————————————————————
P4 排序算法总结
8:56 堆结构 和完全二叉树类似
堆在逻辑概念上是一个完全二叉树结构
10:55 数组转化为完全二叉树结构
任意一个节点 i 的左孩子在数组中的位置是 2*i + 1 ,右孩子是2*i+2,父节点是(i-1)/2
17:00 怎么把数组转化为大根堆
用户的数字是一个一个输入到堆里的,每次加入都和自己的父节点比较,堆只是在2逻辑上是堆,在具体实现上还是数组,所以按照数组的插入即append是从前往后的,所以堆的插入顺序是自下而上的,每次加入与自己的父节点比较就是一个向上浮动的过程
25:30 heapinsert过程
28:00 删除操作,需要完成的是heapify,假设删除了堆顶,那么首先先把堆的最后一个位置复制到头位置,然后heapsize-1,然后heapify。
heapify就是从一个位置出发,然后逐步往下移动的过程
50:00 堆排序
先使用数组构造大根堆,然后拿出堆顶,具体方法是使用堆顶和最后一个元素交换,然后heapsize -- ,然后把剩下的节点重新heapify拿出最大值,而后循环
1:08 整个数组变成大根堆,而不是用户一个一个给数字,该怎么做,所有的节点按从右往左从下往上的顺序进行heapify,heapify的方法就是从上往下滑动
1:17 使用整体的heapify代替heapinsert 来为堆排序算法提速
1:19 堆排序拓展题目:一直一个几乎有序的数组,几乎有序是指每个元素移动的距离不超过K,请选择一个合适的排序算法针对其排序
假设这是一个从小到大的问题,我们就建立一个heapsize为K+1的小根堆,做heapify,把小根堆的最小值放在0位置上。
使用小根堆解决
1:37 比较器
为自己定义的结构告诉系统怎么比大小
对于所有的参数,返回负数第一个参数排前面,返回正数第二个参数排前面
重载比较运算符
1:48 使用比较器让系统构建出大根堆,因为系统默认构建的是小根堆
1:51 桶排序,桶排序是一种不基于比较的排序,不基于比较的排序都是根据数据状况决定的,所以桶排序的应用范围比较窄,要根据数据状况定制
1:53 年龄排序简化版(词频统计表),体现了桶排序的基本概念
1:58 基数排序
首先把所有数字左补0,补到同一个长度,根据个位数字决定数字到哪个桶里,数字先进桶先出桶,把所有数字从桶里按从左往右的顺序导出来,然后根据十位数字进桶,出桶,然后根据百位数字进桶
这个入桶出桶的操作在代码层面做了很多优化,这部分的讲解比较精彩
———————————————————————————————————————————
P5 链表
3:38 各种排序算法的稳定性评估
稳定性是指,值相同的元素在排完序之后能不能保持相对位置不变,基础类型的数据稳定性没有太大意义,稳定性主要会影响非基础类型的排序结果
9:10 选择排序做不到稳定性,选择排序在0-n的范围内选择一个最小值与第0位置做交换,这一步就失去了稳定性,冒泡排序具有稳定性因为总是相邻的两个数字做交换,插入排序具有稳定性,插入排序先0-1位置稳定,0-2位置稳定,0-3位置稳定以此类推,因为也是相邻的两个数字做交换,相同的数字不会交换,所以具有稳定性。归并排序可以做到稳定性,只要在merge的时候保持先拷贝左边的那个相等值,快速排序做不到稳定性,快速排序做不到稳定性,paratation的时候就做不到稳定性了,两种partation的方式(小于等于放左边,大于放右边)。堆排序完全做不到稳定性,堆排的第一步是把整个数组变成大根堆heapinsert,这里就失去稳定性了。
21:53 各排序算法的稳定性、时间复杂度、空间复杂度
一般排序会选择快速排序,如果有空间限制就使用堆排序,如果限制了稳定性,只能使用归并排序。
结论:结论基于比较的排序没有小于o(nlogn)的,同时也没有空间复杂度在o(N)同时还能做到稳定性的排序算法
42:28 哈希表和有序表
哈希表传递基础类型是按照值来传递的,按照自定义的类型是按照地址来传递的
59:22 有序表
———————————————————————————————————————————
P6 二叉树
0:0:53
两链表相交问题:可能有环可能无环,要求时间复杂度o(n)
4:42 判断一个链表是否有环的方法:
使用哈希表:每到一个节点就查询节点在不在哈希表里,不在就添加在表中
12:21快慢指针法
快指针如果指向null,那么链表无环,如果有环,快慢指针会在环上相遇
20:56 解决了两个链表各自有没有环这个问题之后,开始解决链表相交问题
25:33 如果两个链表的结尾不相同,那两个链表一定不会相交,因为不会有类似“X”形状的分叉结构
28:40 链表1无环 链表2无环,
遍历链表1,记录长度为length1,记录最后一个节点为end1,遍历链表2长度为length2,记录最后一个节点为end2,
判断end1和end2内存地址是不是一个,如果不是一个直接返回none
36:29 链表1和链表2一个有环一个没环,这种情况不可能相交,这种结构总会有某个节点有两个next指针,所以不可能
38:18 两个链表都有环
———————————————————————————————————————————
53:56 二叉树的基本结构
58:13 二叉树的递归遍历,递归序,递归序的每一个节点都会返回三次
1:01:44 由递归序得到先序遍历,中序遍历,后序遍历
先序遍历:第一次来到节点打印,第二次第三次啥也不做
中序遍历:第二次来到节点打印,第一次第三次啥也不做
后序遍历:第三次来到节点打印,第一次第二次啥也不做
1:10 非递归行为解决,先序遍历,使用栈
1:18 非递归行为解决,后序遍历,使用栈、
1:22 非递归行为解决,中序遍历,使用栈
1:39 打印二叉树的函数,便于调整代码
1:45 二叉树的深度优先遍历,等于二叉树的先序遍历
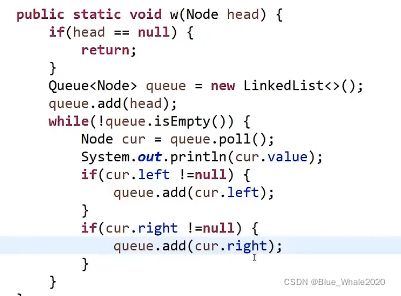
1:46 二叉树的宽度优先遍历,使用队列
(1) 头节点放队列中,然后弹出,弹出就打印,先放左再放右
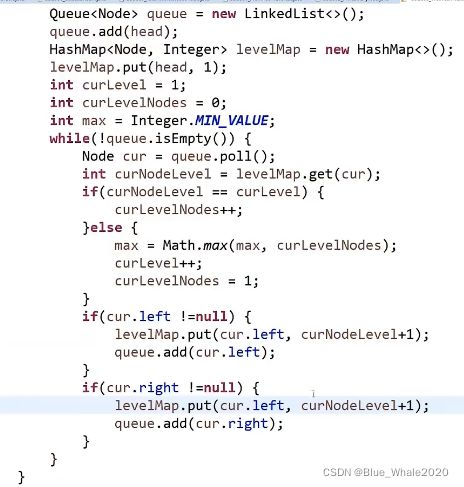
1:50 求一棵二叉树的最大宽度
除了简单的宽度优先遍历,我们还得设计一种机制,让代码知道当前节点在第几层
加入一张哈希表levelmap,头节点肯定是第一层。设置一个变量curlevel,记录当前在哪一层。设置一个变量curnode,记录当前层发现了几个节点。设置一个全局变量max,用来得到所有层哪一层节点是最多的,一开始等于系统最小
2:10 不用哈希表的方法求宽度
———————————————————————————————————————————
P6 图
2:31 怎么样判断一棵树是不是搜索二叉树
搜索二叉树 左树的节点都比根节点小,右树的节点都比根节点大
使用中序遍历来完成判断,之前的打印行为变成了动作
20:40 如何判断一棵二叉树是不是完全二叉树
完全二叉树:二叉树不满的节点必须从左到右排列
标准:1、有右孩子无左孩子返回false 2、在第一个条件不违规的情况下,第一个左右两孩子不全的情况,接下来的所有节点都必须是叶节点
34:10 如何判断一棵二叉树是满二叉树?
使用函数分别统计二叉树的深度和二叉树的节点个数,这两个数字之前有比例关系
37:15 二叉树的解题套路
38:00 使用这个套路判断二叉树是不是平衡二叉树
左树平衡,右数平衡,左右两树的高度差不能超过1
1:10 使用套路判断满二叉树
1:23:46 寻找最低公共祖先
1:48:07 找到一个节点的后继节点(中序遍历中一个节点的下一个节点)
后面讲了一种结构上的方法,不必使用生成中序序列再查找的方式
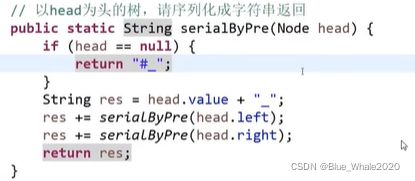
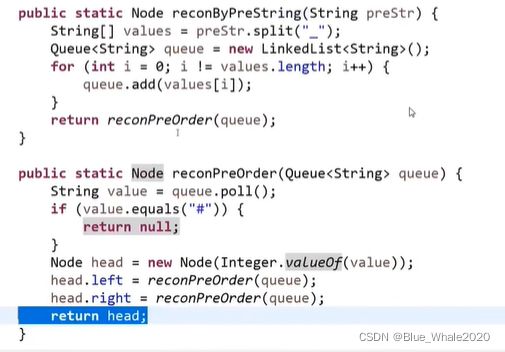
2:02 二叉树的序列化和反序列化
讲二叉树转化为具有结构的字符串 或将字符串转化为二叉树
有先序遍历序列化,中序遍历序列化,按层遍历序列化
2:15 微软的折纸问题
———————————————————————————————————————————P8 详解前缀树和贪心算法
3:00 图的基本概念
有效图和无效图
5:00 由图引申出的直接邻居
6:50 邻接矩阵表达图
17:30 常见图的表达方法
26:16 数据结构之间的转化(这个部分是重点)
40:00 宽度优先遍历
50:00 深度优先遍历
59:32 拓扑排序,如编译顺序的问题
1:12 最小生成树算法 P算法
1:59 Dijkstra算法,单元最短路径算法,这种方法要求权值没有负数的边,具体来说是不能出现一个累加和为负数的环,这样就会导致节点A走一大段回到自己的距离,比自己到自己的距离还要远,然后每转一圈都会越来越小
———————————————————————————————————————————
P9 暴力递归
5:17 前缀树的概念
由字符串画前缀树
30:00 查询某一个单词加入过几次
35:00 查询有几个字符串是以“XXX”作为前缀的
37:00 删除
———————————————————————————————————————————
59:37 贪心算法:基于莫一种标准进行排序,不从整体考虑,只求局部最优解
1:02 贪心算法实例 会议室问题
一些项目要占用一个会议室宣讲,会议室不能容纳两个项目同时宣讲,给一批项目的开始时间和结束时间,使会议室的场次最多
哪个会议结束时间早就安排谁
1:18 数组中有很多字符串,使用一种顺序将字符串的顺序都拼接起来,字典序
1:29 字典序排列贪心策略的证明 证明贪心排序策略是正确的 有传递性
1:52 一根金条切分成两半 是需要花费和长度数值一样的铜板的,一群人想要分整块金条,怎么分最省铜板
哈夫曼编码问题,贪心策略堆和排序是最常用的技巧
2:04 花费-收益-启动资金-最多能做几个项目
利用小根堆排序花费 利用大根堆排序利润
2:17 取得数据流中数字的中位数
利用大根堆和小根堆,保持较小的那一半数字在大根堆中,较大的那一半数字在小根堆中,一道经典题,输入一个数,看这个数字是不是小于大根堆的堆顶,是则进入大根堆,否则进入小根堆,然后比较两个堆的大小,如果两个堆的size之间超过了2,那么size大的那个就把堆顶弹出到size较小的那个里面,没有代码。
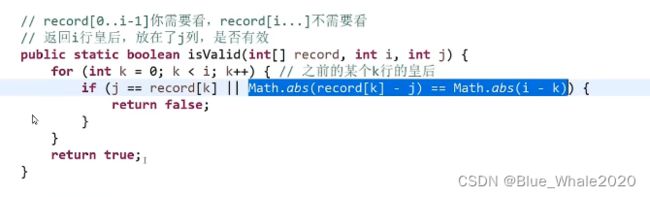
2:27 n皇后问题,一个n*n的棋盘上,摆上n个皇后,皇后不同行,不同列也不能在一个斜线上,需要返回共有集中摆法
2:48 皇后的常数级优化范围方法
———————————————————————————————————————————
补充视频
DJ特斯拉算法的加速
使用小根堆为找最小值的过程加速,但是不能使用系统提供的堆,系统使用的堆做不到针对某一个特定的节点调整
43:00 暴力递归
暴力递归尝试
1、把问题转化为规模缩小的同类问题的子问题
2、有明确的不需要继续进行递归的条件(base case)
3、有得到了子问题结果的决策过程
4、不记录每一个子问题的解
44:40 汉诺塔问题
57:30 打印一个字符串的全部子序列,包含空字符串
1:06 打印一个字符串全部的排列,1:18 递归中的分支限界
打印一个字符串的全部排列,要求不要出现重复字符串
利用交换解决
1:23 题目八 代表不同数值的纸牌排成一条线,玩家A和玩家B依次拿走纸牌,规定玩家A先拿,玩家B后拿,但是每个玩家只能拿走最左或最右的纸牌,同时玩家A和玩家B都决定聪明,请返回最后获胜者的分数
两种不同递归函数
1:32 给你一个栈,请你逆序这个栈并不能使用额外的数据结构,只能使用递归函数
递归函数技法的训练
递归套递归
1:40 规定1和A对应 2和B对应 3和C对应
那么字符串111就可以传华为AAA、KA、AK三种
给定一个数字字符串,返回有多少种转化结果,递归方案里加上if 多种判断
1:54 给定两个长度都为N的数组,weight和values分别代表物品的重量和价值,同时给一个能载重bag的袋子,你装的物品不能超过这个重量,返回能装下最多的价值是多少
2:03 N皇后问题
———————————————————————————————————————————
P11 基础提升 哈希函数与哈希表
3:42 哈希函数
1)输入无限,输出有穷尽。2)同样的输入对应同样的输出,没有随机因子 3)哈希碰撞,不同的输入会导致相同的输出,但是概率非常低 4)最重要的性质,输出的均匀性和离散性
19:00 对在S域上均匀分布的输出取模为m,则取模之后的输出在m域上也是均匀分布的
21:15 补充题目,一个大文件中的所有文件都是以无符号整数的形式编码的,一共有40亿个,如果只提供1G的内存,想要返回出现个数最多的数字
如果单纯使用哈希表来统计,使用字典格式来统计词频,1G内存不够用
休息之后后面会讲到,即使出现了碰撞的问题,但是在每一个小文件里会使用哈希表做精细的计数,所以碰撞问题不会影响到最后的结果
36:52 哈希表的实现
通过哈希函数计算每一个key对应的哈希值,然后将这个哈希值取模(比如17),取模结果得到5,那么就把这个key+value,以单向链表的方式串在编号为5的桶里。
如果哈希表发现自己某一个链过长(由于哈希函数的均匀性,其他链的长度也不会短),那么就会触发扩容逻辑
后面有关于计算、扩容和查找的复杂度运算
52:13 具体语言中哈希表的其他改进
1)开放地址法
54:20 题目:设计RandomPool结构,做到三种功能:1、insert 做到不重复加入 2、delete 将某个key移除 3、getRandom,等概率随机返回任何一个key,要求三种方法时间复杂度都是o(1)
没有有关哈希表的知识,纯粹的code技巧
1:07 布隆过滤器
公司有100亿个url组成的黑名单,只需要提供加入和查询两种操作,不需要提供删除
使用哈希表可以满足这个需求,但是需要过量的内存占用
布隆过滤器会存在把白名单数据转为黑名单的错误,而且这种错误率虽然较低但是不可避免
1:19 位图的概念
int类型的数组中的每一个格子 4字节 32个byte
long类型的数组每一个格子8个字节 64个byte
位图是byte类型的数组,每一个各自1byte
1:22 如何做出一个byte类型的数组,以及找到位图上的元素、获取他的状态、修改为1或修改为0操作
1:30 布隆过滤器就是一个大位图、布隆过滤器的工作过程
1:38 什么决定了布隆过滤器的失误率
1、位图长度,位图长度m越大 失误率越低
2、哈希函数的数量k,随着k的增多,失误率先减小后增大
1:45 布隆过滤器的三个公式,布隆过滤器的设计过程,公式的结果向上取整
布隆过滤器的思考前提是,允许有一定的错误率,没有删除行为,使用场景是类似黑名单记录的行为
布隆过滤器的设计和样本量和失误率有关
1:55 一致性哈希
用来讨论数据服务器如何组织
———————————————————————————————————————————
P12 基础提升,有序表和并查集
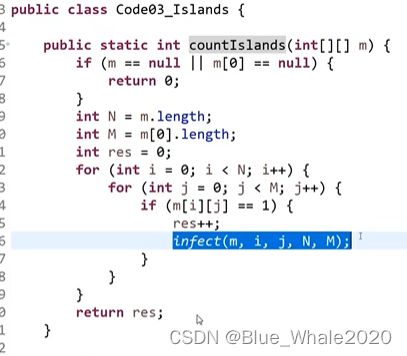
岛问题:一个矩阵中只有0和1两种值,一个值只能和自己的上下左右相连,如果有一片1连在一起,那么成为矩阵中有一个岛,给定一个矩阵,求矩阵中一共有几个岛?
感染过程可以把连篇的1变成2,然后只要找矩阵中剩下的1,不断的进行感染,最后走了几个感染过程就有几个岛
首先遍历所有的岛,每遇到一个1,就把所有的1都感染成2,然后让结果+1
感染是一个递归过程,basecase的确定比较容易,上下左右不超过边界,当前位置的被感染者必须是1
16:00 感染问题的时间复杂度
19:36 如果使用并行手段解决这个问题
如何使用将矩阵分片来解决这个问题
25:00 并查集结构
支持集合快速合并的操作,问题的引出
我需要查询两个集合是不是同一个,如果不是同一个就union在一起,而这种操作在不同的数据结构所需要的复杂度是不同的。比方说链表,想要union只需要将链表接在一起就行了,但是is same set操作会很慢,只能一个一个遍历。比方说哈希表,is same set会很快,只需要看B集合里面有没有A,A集合里面有没有B,但是union操作会很慢,所以是否存在一种结构,让 union操作和 is same set操作都很快,这就是并查集要解决的问题。
并查集是一种不断向上查找的图结构,属于同一个集合的顶端节点是相同的
37:00 并查集结构向上查找的过程的重要优化
在某一个链向上查找父节点的过程中,需要把这个链上的每一个节点直接指向根节点,让其扁平化
40:00 并查集结构代码
1:00:01 并查集结构的复杂度,在一个并查集结构中,findhead的调用次数越多,单次的平均复杂度越低
1:05 回到岛问题,怎么样做到并行
由于并行计算需要把矩阵“切开”,去交给不同的CPU,这个切开的过程会让原本的连通性消失,所以还需要手机边界信息,这部分没讲怎么具体实现,左说只有面试到牛逼的公司会遇到这种问题。
1:21 KMP算法
有字符串str1和str2,问str1是否包含str2,如果包含返回其实位置,要求时间复杂度o{N)完成
经典一个一个比较的办法时间复杂度高
1:34 开始正式讲
最长的前缀和后缀的匹配程度,一个字符都带有一个信息,而这个信息和字符本身无关,和这个字符前面的字符有关
设一段字符串 abbabbk
那么k的信息是这么得来的
前缀长度 后缀长度 前缀 后缀 是否相等
1 1 a b F
2 2 ab bb F
3 3 abb abb T
4 4 abba babb F
5 5 abbab bbabb F
那么前缀后缀相等的最大长度是3 ,k的信息为3
有这个了解之后就可以得到一个数组的nextarr
后面有关如何利用nextarr的特性就非常精彩了!
2:18 一个例子展示完整的过程
str1: a b b s a b b t c a b b s a b b e
str2: a b b s a b b t c a b b s a b b w
发现e和w不同,w的next值为7,那么就跳到t,相当于比对
a b b s a b b e
a b b s a b b t
发现e和t不相同,t的next值为3,那么就跳到s,相当于比对
a b b e
a b b s
发现e和s不同,s的next值为0,就跳到a,相当于比对
e
a
发现还不同,那么,str1的比对位置e往后移动一个,意思就是整个str1配不出str2了
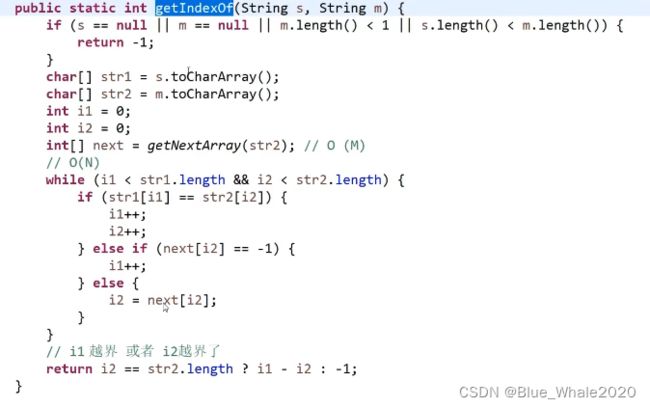
2:23 KMP算法的代码
i1是str1中待比对的位置,i2是str2中待比对的位置。
在比对的过程中,要求i1不越界,i2不越界,如果i1和i2对应的字符相同,则一起+1,如果不相同,就要求i2往前跳(根据next数组)。如果i2来到了零位置(next[i2]==-1 或者写为i2==0),那么i2没法往前跳了,需要i1换一个位置比对
2:47 怎么求解Next数组的代码
想求得i位置的最大前缀,需要用到i-1位置的最大前缀信息(如7),接下来比较str[i-1]和str[7],如果相同则i位置的信息为7+1 = 9,如果不相同,在cn>0(待比对位置cn还没有来到数组头部,即还可以往前跳),那就根据自己的next信息跳到往前的位置
———————————————————————————————————————————
P13 基础提升Manacher算法
马拉车算法
Manacher算法解决的问题,字符串的最长回文子串如何使用O(N)的时间复杂度求解
7:00 回文问题的经典解法暴力解法,以一个字符为中心向两边扩充,但是这种办法会错过长度为偶数的回文子串,解决办法是在每两个字符之间扩充字符,这样奇数次字符和偶数次字符都能比对到。这种方法不要求新添加的字符是原字符串里没有的,因为后添加的字符和新添加的字符之间不会相互影响
21:00 开始讲manacher算法,回文直径、回文半径、回文半径数组、最右回文右边界的概念,C为取到最右回文右边界时的中心
记以C为中心的回文区域左边界为L 右边界为R
情况1: 中心点i不在最右回文右边界中,则以中心点i为中心暴力扩充
情况2:中心点i在回文右边界R中,那么取得这个回文右边界的中心点C一定在i的左侧,根据C做i的对称点i*
情况2.1 如果i*的回文区域完全在以C为中心的回文区域中,那么i的回文半径大小和i*回文半径大小相同
53:00 情况2.2 i*回文区域的一部分位于以C为中心的回文区域外侧,则此时i自己的回文区域是i到R这一段
1:02 情况2.3 压线情况 我们不需要验证从i到R的那一段,那里不是回文,需要验证的是从R往右是不是回文数
1:16 时间复杂度
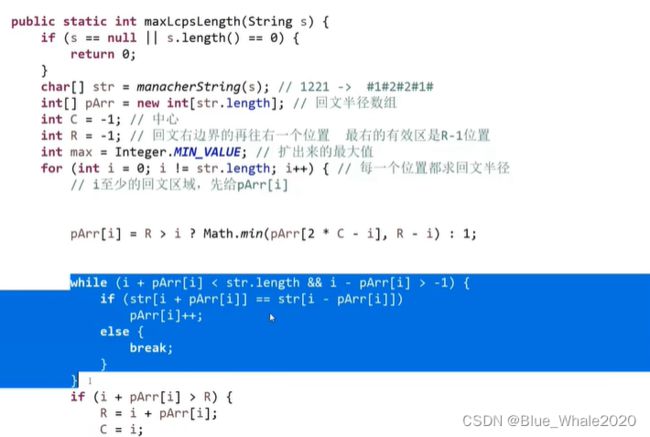
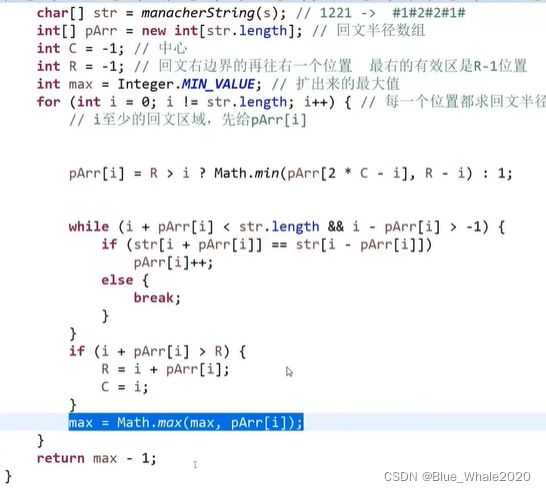
1:21 manacher代码,manacher方法不仅能解决回文子串的问题,回文字符串数组的概念能解决很多同类问题
返回的是原串的回文直径,如121的回文直径是3,但是max在代码中是经扩充后字符串的回文半径,如#1#2#1#,是4,这两者之间有一个减1的关系
1:40 窗口最大最小值结构(他说这几种结构被火车撞了都不能忘)
有一个整型数组arr和一个大小为w的窗口从数组最左边滑动到最右边,窗口每次右滑一个位置,要求输出arr和窗口大小w,返回每次滑动窗口的窗口内最大值res,res应该有n-w+1这么多个
可以选择R往右移动或者L往右移动,移动的过程需要保证L不会出现在R左侧
R动代表有一个数字被纳入到窗口中,L往右动代表一个数字被移除出窗口
1:49 算法流程
双端队列:可以从头部进出节点或尾部进出节点
流程:当R往右动的过程中,数字从右侧尾部进入双端队列,双端队列从始终保持单调性,头部节点最大,到尾部一次递减。如果新进来的数字发现自己会破坏队列的单调性,那就把队列内之前的数字弹出,弹出的数字不找回,一直弹出直到队列为空,或者新数字的进入不会破坏单调性
在L往右动的过程中,势必会导致队列中的一些数字过期,这时只需要检查过期数字是不是位于队列的头部,如果是:则从头部弹出,如果不是:则不做任何操作
2:11 单调栈结构
有一段整数数组,54672301 ,想得到任意一个整数x右侧,离x最近的比x大的数字。和x左侧离x最近的比x大的数字
2:16 单调栈的工作过程
单调栈需要维持从栈底到栈顶由大到小,如果新进来的数据可能破坏这种单调性,那就将之前的数据弹出,弹出的数据就地生成信息,当遍历到整数数组的结尾,栈里还有数字的时候就开始清算,依次弹出,每次弹出就记录他的信息
2:22 这种方法为什么是正确的
2:31 数组中有重复值的情况
2:39 单调栈的例题,定义:数组中只有正数,数组中的累计和和最小值的成绩,假设叫做指标A,给定一个数组,请返回子数组中,指标A的最大值(子数组是连续的)
我们只要遍历每一个数字,找到以当前数字i为最小值的子数组,这样考虑问题的话,很容易转化到单调栈的问题
———————————————————————————————————————————
P14 基础提升 活动窗口 单调栈结构
树型dp的套路
使用前提:如果题目的求解目标是S规则,则求解流程可以定为每一个节点为头节点的子树在S规则下的每一个答案,而且最终答案一定在其中
3:19 二叉树节点之间的最大距离问题
从二叉树的节点a出发,可以往上或者往下走,但沿途的节点只能经过一次,到达b所经过的节点数是a到b的距离,求整棵二叉树的最大距离
情况1: 根节点root不参与,那么最大深度来自于其左子树最大深度或者右子树最大深度
轻狂2:根节点root参与,那么最大深度来自于其左子树最大距离+右子树最大距离+1
精彩的递归思路详解
22:32 派对的最大快乐值
多叉树的数据结构
以头为x的参与还是不参与的细分
35:52 大活! 二叉树遍历中最炫酷的:morris遍历
一种遍历二叉树的方式,空间复杂度o(N),时间复杂度o(1),通过利用原树中大量空闲指针的方式,来达到省空间的目的
在不允许修改二叉树结构的题目中,morris是没法用的。笔试中不建议使用morris比较复杂,面试推荐
向右移动指的是向自己的右孩子移动
43:00 流程例子
从morris遍历的结果来看,如果一个节点有左树,那么一定可以出现两次,没有左树的节点只能到达一次
既然有左树的节点会来到两次,能不能知道是第几次来到这个节点? 可以,可以观察左树上mosttright节点的指向,如果指向null,那么是第一次来到。如果指向cur,那么是第二次来到
58:00 morris遍历的代码
1:05 时间复杂度和空间复杂度
1:10 如何使用先序和中序遍历得到morris遍历
一个满二叉树的morris序为1242513637
先序遍历:如果一个节点只到达一次,直接打印,如果可以到达两次,则第一次打印,那么就是1245367
1:15 中序遍历:一次的节点直接打印,两次的节点,第二次打印
1:18 后序遍历 :能回到自己节点第二次回到自己的时候,逆序打印自己的左树的右边界,当所有遍历结束,打印整棵树的有边界,退出
1:30 如何做到逆序打印,却不带来额外的空间复杂度,使用单链表的逆序操作(这里是二叉树的右子树逆序),然后在打印之后还原
1:33 morris遍历的应用:如何判断一棵树是不是搜索二叉树
中序遍历的过程中:如果结果是升序的,那么就是搜索二叉树
1:38 两种套路:1、二叉树递归 2、morris遍历的使用时机
如果发现这道题必须用第三次回到自己的信息强整合才能解决,那么就是用二叉树的递归套路,具体来一个节点必须先收集自己左树的信息,再收集自己右数的信息,然后回到自己做信息整合,
如果不必用第三次信息的强整合,那就morris遍历为最右解
———————————————————————————————————————————
有关大数据题目的解题技巧(前4个在之前的课程中提到过):
1) 哈希函数可以把数据按照种类分流
2)布隆过滤器用于集合的建立与查询,并可以节省大量空间
3)一致性哈希用来解决服务器的负载和管理问题
4)利用并查集做岛问题的并行计算
5)位图
6)分段统计的思想
7)利用堆、外排序做多个处理单元的分段合并
———————————————————————————————————————————
1:40 题目1:无符号整数都是32位的,现在有一个包含40亿个无符号整数的文件,要求只使用1GB的内存,找到哪些无符号整数是没在这个文件里出现过的。
这个基础问题在P11里面提到过
范围是0-2^32-1,我要准备一个相应的btye类型数组,需要2^32 / 8这么大空间,约为500M
进阶: 内存为3KB,只需找到一个没出现过的数
我们开辟一个无符号整形数组做词频统计表的话,那么这个数组的长度为 3KB/4 大约为512,所以我们使用一个int[512]这么大的数组.又因为代存储的数据是32位的,32位无符号数据的范围是2^32,那么可以推得,每一个int[i]数组里最大能累积的数为 2^32 / 512 = 83388608个。
在程序开始运行后,我们把每个带存储的数除8388608,就能知道这个数字该落在int数组的哪个桶内,当运行完所有的计算之后,肯定有一个桶是不满的,因为待存储的数据共有40亿个,小于32位无符号整数可以表示的范围
———————————————————————————————————————————
P15 基础提升 二叉树的morris遍历等
前面大数据的题目不感兴趣跳过了
位运算的题目
从1:06 给定两个32位有符号整数a b,返回a和b之中较大的那个,要求不做任何判断
首先可以将一个数字向右移动31位得到她的符号位,从而判断正负
然后让a-b,得到的结果的符号,
1:15 考虑到a-b可能会溢出的情况
1:23 判断一个32位正数是不是2的幂和4的幂
2的幂是2进制位中只能有一个位是1,然后让这个二进制数减1,那就会把唯一的1打散,如果x&(x-1) = 0,那就证明有唯一一个1
4的幂 2进制位中也是只能有一个位是1--条件1,而且这个1只能出现在0位、2位、4位、8位
在条件1的前提下,让x&(0101010101) =Z,如果Z不等于0,那就是4的幂
代码 1:33
1:34 卧槽感觉爆难,给定两个32位有符号整数a b,不使用算数运算符,实现a b的加减乘除操作
1:36 解决加法,首先对两个数字a和b异或,相同为0不同为1,异或是一种无进位加法,接下来我们需要得到进位信息,进一步,做a与b,得到进位信息序列,将这个进位信息序列左移一位,得到进位结果,接下来我们将进位结果和亦或结果相加(包括亦或+进位信息序列左移),我们重复这个过程,知道不再产生进位信息 代码在1:44
1:47 减法 b取反加1得到b的相反数,然后a 加b的相反数就是 a-b
1:48 乘法 二进制的乘法运算和小学时候的乘法运算是一样的 代码1:52.
1:59 最难的除法,现在要求 a/b ,先把b尽可能的往左移动以接近a,老师这种方法不太好理解,建议直接看视频,关于这个事情的理解,00101乘01100,其实代表的就是00101左移2位加上00101左移3位的结果,同理0111100除00101的过程中,发现00101左移3位能让0111100恰好剪掉他,那就在结果中记录上01000,对应了相乘过程中的左移结果除法的代码在2:10,2:12是代码流程,这个代码里使用的是被除数左移来替代了除数右移,因为除数右移可能会改变除数的符号位,然后导致结果错误,res |=,就是因为同一个位上的1只能出现1次,所以直接或就行了。
———————————————————————————————————————————
P16 大数据题目
9:23 阿里面试原题,机器人问题
int N = 1,2 ……N
int S = 1,2 ……N ,机器人的起始位置
int E = 1,2 ……N,机器人的运动目标,在机器人必须走K步的情况下,从S到达E共有多少种方法
16:00 代码,27:39,把这个递归函数拆开来看之后,看看还有哪些可以优化的地方,这个递归中存在很多重复解,我们需要一个表结构,把每一次递归的结果记录下去,这样就可以避免重复计算,比如都是f(2,2),虽然调用f(2,2,)的函数不一定相同,但是两个f(2,2)的返回结果是相同的,这种叫做无后效性的动态规划,无后效性是指函数的返回和之前的状态无关,在面试中的大部分dp都可以改成无后效性dp,所以说,dp的第1步优化就是记忆化搜索,35:05,进一步地,整理位置依赖,改成表结构动态规划的版本,48:00。根据递归的过程依赖关系推出来的
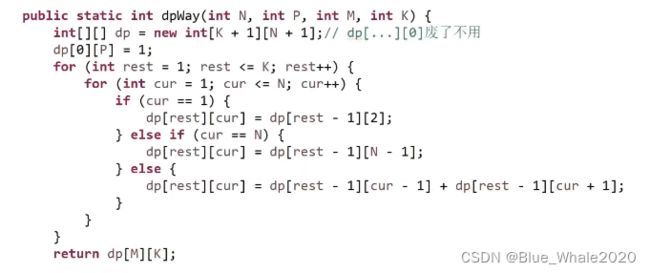
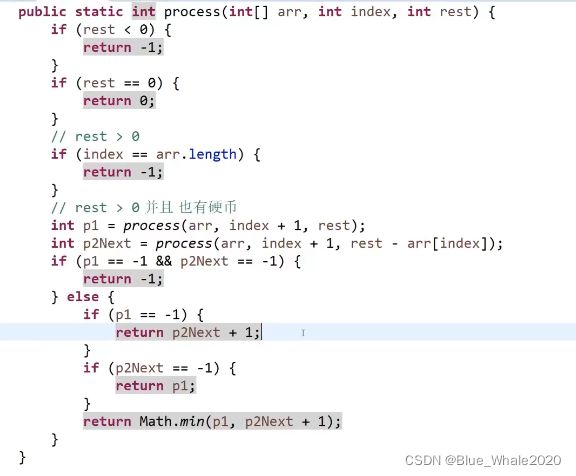
1:00 另一道例题,一个正数数组,其中每一个数字代表一个硬币的面值,现在给一个输入K,请问最少需要几个硬币能组出这个K,1:22,改出了最终版本的代码,1:24开始解释递归过程
1:32 开始记忆化搜索优化,在初始化表的时候,由于代码里-1用来指代无效解,0代表答案,那就用-2初始化这张表,-2代表这个节点算还是没算过。同时如果表的其中一个维度有负数,那就在代码中保留他,把代码中的所有return都记录在表的格子里就行了
1:45 动态规划表
课程总结:递归尝试的方法的一旦确定,记忆化搜索的方法就是加傻缓存,变成严格位置表依赖的方法,严格表方式:1、分析可变参数的变化范围 ,2个可变参数就是一个二维表 2、在表中标出要计算的终止位置 3、在表中根据basecase标注不用计算直接出答案的位置 4、推出普遍位置是如何依赖其他位置的 5、定出严格表的推理计算顺序,从哪些格子推到哪些格子 6、上面确定了之后,之后copy递归的方法
———————————————————————————————————————————
P17 暴力递归上
例题:两个人都能看到数组上的所有数字,两个人轮流玩游戏,每个人只能拿最左或最右,这个题之前说过,问谁拿的最多,返回获胜者的分数
s函数math.min的原因是,返回的是我所能得到的分数,但是控制权不在我,对方肯定会给我留下,在我下一步中所能选择的最少的那个,s函数和f函数都是我当前步能得到的信息,而“当前步”这一概念是和未来的选择有关的,这是一个递归函数,只有在来到最后一步时,当前步才不会和未来步相关
13:33 记忆化搜索和改动态规划
由于i小于j,所以这张表左下半区是无效的
然后这里面会有一种互相调用的问题,会比较难改表格,做熟悉了就好了 代码 28:49
29:10 三维动态规划
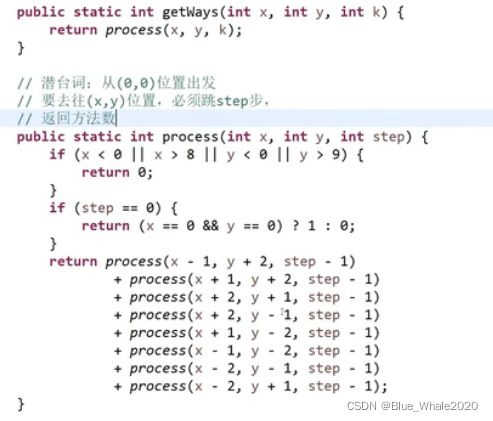
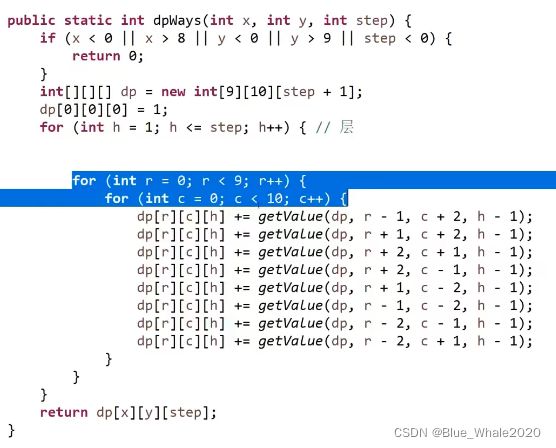
中国象棋,马停留在左下角,给出a,b 就是马要去的位置,马一定要跳k步,到ab的方法数有多少,这个代码是反过来走了
50:35 开始改动态规划,做表,其实是做一个体
1:05 下一道例题
给定一组 x,y 确定了这个格子有多大,(a,b)代表Bob在格子里的位置(可能越界),Bob要走k步等概率,一旦越界Bob就会死,问Bob活下来的概率有多大,
先返回bob活下来的次数,可以理解为long live = 0 ; live += ;live+=;live+=;live+=;,就是在每一层递归都把live初始化为0就行
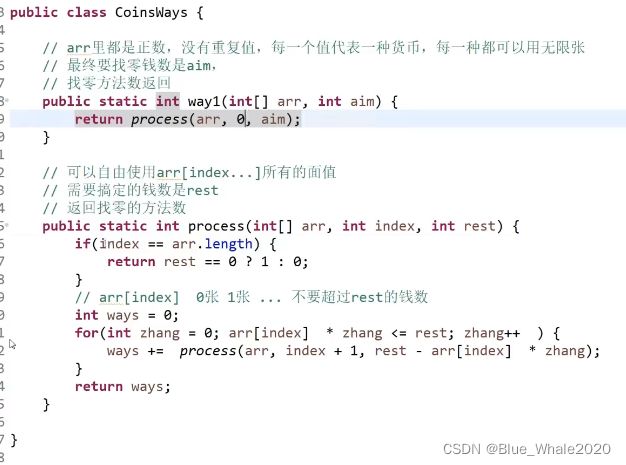
1:19: 给定一个数组,里面所有的数值都是正数,每一个位置的值代表一个面值的货币,一个面值代表可以使用任意张,要组出一个钱数,问方法数有多少种。这是在一个递归里面。使用for循环多次迭代下层递归的例子
basecase代表已经没有面值可以选了,看看目前位置搞定还是没搞定
1:28:07,如果有了动态规划表了之后,出现了一些枚举行为,怎么规划
f(0,1000)代表,0及其后面的货币自然选择,1000代表需要搞定1000,这个index之后自然选择的这个概念,老师好像经常用
准备一张二维表,有n+1行,因为index能达到n,有aim+1列,因为aim会取到0
改成动态规划就是直接抄递归行为,把递归改成之前的取值行为就行了
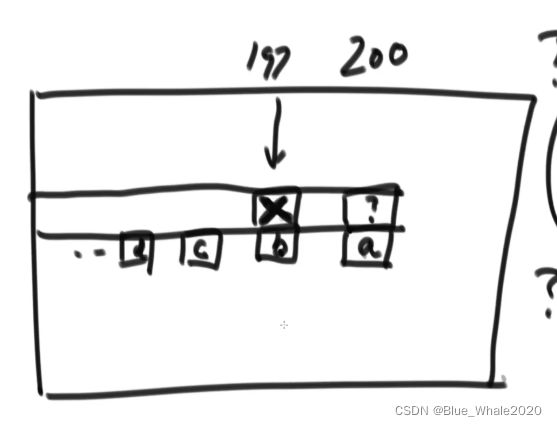
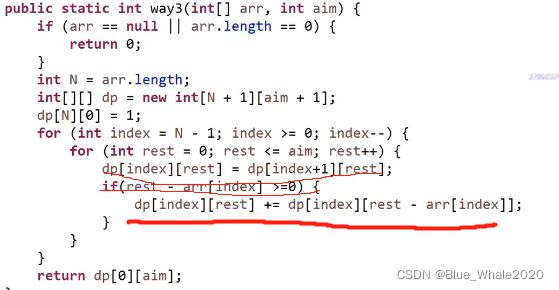
1:45 优化之后时间复杂度的计算,重点来了,在上面动态规划的版本中,有3个for循环,在求单独的一个格子的时候,存在枚举行为,就是一个格子的得出要累加下面的所有格子,这种枚举行为真的有必要吗? 没有!!,开始斜率优化,如果一个动态规划中有枚举行为,那么观察这一点的数值能不能有临近的点得来
这个?位置完全可以由这个x位置的值加a位置的值得来
改了这三行代码,首先一个格子的数值总是需要自己的下一个格子,此外还需要与本行中与自己相邻的【rest-arr[index]】的格子,
2:07,怎么评价自己想出的尝试方法的好坏,1)每一个可变参数自己的维度 最好就是一个整数,整数的变化范围远远比数组小 ,如果一道题需要单个可变参数突破0维的尝试方法,这种题一年不会超过5道题 2)参数的个数 ,参数个数少,维度就小
———————————————————————————————————————————
P18 基础提升-暴力递归(下)
有序表
7:46 有哪些结构可以实现有序表,红黑树、AVL树、Sizebalance tree(SZ)、跳表skiplist
前三个是平衡搜索二叉树系列 BST
12:55使用搜索二叉树来满足增加删除查找的要求,在不考虑平衡性的时候,用户每给一个数,大于根节点就右移,小于根节点就左移,如果搜索二叉树有了重复节点,就在当前节点加数据项就行了
有序表输入key =i,有序表能返回比i小的距离i最近的节点,使用搜索二叉树实现的话,就是从根节点往下滑动,遇到小于i的就先记录下来,然后去右子树上找,遇到大于i的就去左子树上找
19:00 搜索二叉树的删除
删除有两种简单的情况,第一种情况是要删除的节点是叶节点,另一种情况是要删除的节点不是左右两个孩子都全,直接让唯一的孩子替代被删除的节点位置就行了。麻烦的就是两个子树都全,这是可以选择左树的最右节点或者右数的最左节点
27:00 但是搜索二叉树没有平衡性,所以时间复杂度会很受输入数据的影响,但是不需要保证严格的平衡性,只要保证左树和右树的规模不要差太大就行了
32:00 AVL树是严格的平衡性,我们可以在搜索二叉树上实现左旋和右旋,使其成为带有自平衡操作的搜索二叉树,在此基础上,再使用上左旋和右旋就成为了AVL
34:00 开始讲解左旋和右旋,左旋和右旋可以调整平衡性
40:00 有关AVL树是怎么查到自己不平衡的,42:00,AVL树的检查时机是增加和删除的时候,删除是更复杂的情况
45:00 有关avl树的检查怎么查,存在四种平衡树平衡性被破坏的情况
1、LL型 左树的左边过长,直接右旋就行了 2、RR型 右树的右边过长,直接左旋就行了 3 LR形,就是把左树上过长的那条边的根节点,一直通过左旋和右旋调整至头节点 4、RL型
53:00 怎么确定是4种类型中的哪一种,code
红黑树和SB树的平衡标准是什么
1:04 SB树平衡性的定义,的每个子树的大小,不小于兄弟树的子树大小,就是叔叔的子树和侄子的子树比较 1:07 几种不平衡性的定义和对应的调整方式。
LL型:左子树的左子树大小,比右子树大
1:24 红黑树 说红黑树太难了 没必要学
1:32 跳表 1:47 调表的大规模举例,前面是小例子,1:55 跳表查找 1:57 调表的高度是和数据量有联系的,差不多等同于满二叉树
2:01 社会嗑
会用哪些产品,项目经历突出技术和解决了什么问题,个人评价对技术的看法是什么样的人
AWS 阿里云 火的概念 技术产品,该实现的产品 对比,产品对比,编项目,重点在于会不会这个新业务,需要调研比较热门的技术,这是一个学习路线
———————————————————————————————————————————
中级提升班1:
主要是刷题:
贪心策略,把绳子最右侧的点放在一个存在的点上,然后从右往左看,把绳子左侧的端点定位在数轴上,然后在数轴上找到大于等于左侧断点处最左的位置(二分法),然后下标计算得到长度
更好的方法
滑动窗口
确定一个左指针,每次定位在数轴中的每一个点,确定一个右指针,根据做指针再往左推L个位置。由于左右指针都不回退,所以整个时间复杂度为O(N),没有代码
16:37
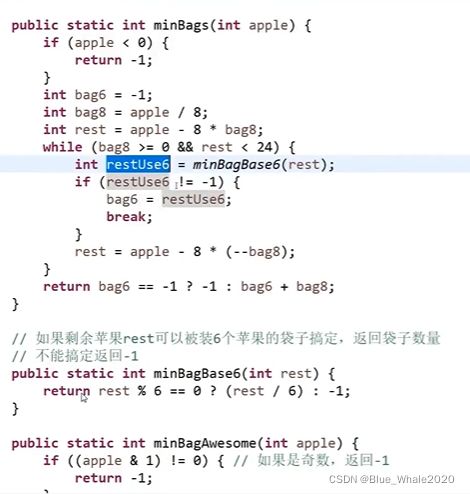
简单的策略是先尽量使用8类型的袋子
这里一个取巧的方法是,当剩余未搞定苹果的个数大于24个的时候,就不用接着试了。考虑一下大于24这个数字是怎么来的,假设一个大于24的数字M,那么M可以分解为m+24,那么肯定是之前使用了3*8个,剩余m,发现m用6整除不了,然后用2*8个,剩余m+8用6亦然整除不了,直到m+16,m+24,如果想用6解决m+24的话,其实6要先解决24,然后发现m之前已经算过解决不了了。
38:44:当发现一道面试题,入参是一个整数,出参也是一个整数,那么先写出特别傻的代码,然后分析规律,做优化
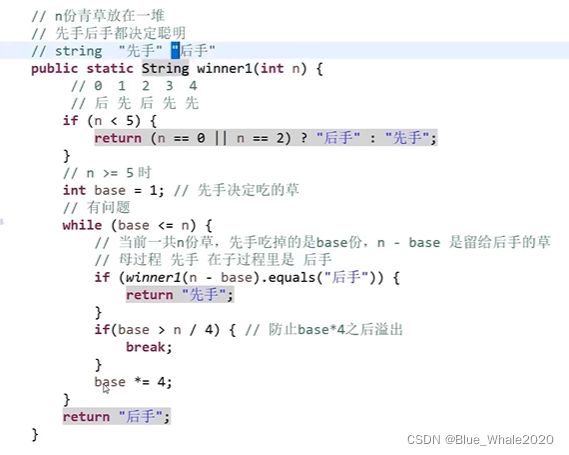
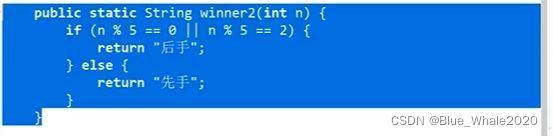
44:30 举例,关于先后手的递归+循环中的递归
先手和后手两只动物吃草,草的总数是一定的,每次规定只能吃4的n次方那么多草,请返回谁会赢
第20行中,winnner(n-base)是子过程,子过程中后手胜利,代表母过程即先手胜利,while中每次尝试自己吃更多的草能不能赢
1:05,这个递归的过程讲解,然后你打印这个结果,再总结规律,
得到下面的代码
预处理的技巧 1:10
我生成两个辅助数组,其中一个数组统计从左到右有几个G,一个从右到左统计有几个R,做的时候取一个分界线,分界线左边都是准备染色为R,分界线右边都是准备染色为G
1:28
一个矩阵中有几个子矩阵,时间复杂度是o(N^4)的,因为点两个随机的点,两个随机点的概率都是o(N^2)的,再相乘(构成一个矩阵),复杂度就成了o(N^4)了。正方形的概率是o(N^3).
使用两个for循环分别枚举长和宽,代表了任何一个左上角点的随机位置,使用第三个for循环来枚举边长(存在一个竖着先到边界或者一个横着先到边界的问题),再使用一个right矩阵和一个down矩阵,分别记录每一个点右侧有多少连续的1,记录每一个点下面有多少个连续的1
1:56
这种问题需要使用二进制来拼凑,先用1-5的等概率,产生等概率返0-1的,1-2返回0,4-5返回1,3返回重新来
等概率返回1-7,其实就是等概率返回0-6
只要数6有几个二进制位,需要3个,生成7的话就重做
第二问和第一问一样,第三问就连续生成两次,如果生成00或01就重做,得到10就算1,得到01就算0
———————————————————————————————————————————
中级提升班-2
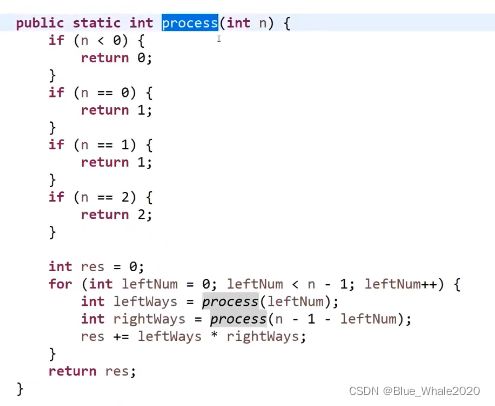
给定一个非负整数n,代表二叉树的节点数,请问共能生成多少种二叉树的结构
假设N个节点的种类是F(N),假设左数有i个节点,左数可能性就是F(i),那么右数的可能性就是F(N-i),总共的可能性九四F(i)*F(N-i),这里的i是从0变化到N-1的,把这些可能性全加起来,就是总的F(N)
code
8:00 括号串
我们应该怎么判断括号完整还是不完整,从左往右遍历一遍遇到左括号就count++,遇到右括号就是count--,第一个标准是,整个遍历的过程中不能出现count小于0的情况,第二个标准是遍历结束之后,count必须等于0
code:15:20
遇到的右括号,但是此时count为0,就说明之前没有多余的左括号可以和这个右括号配对了,所以直接在answer中加一就行了,代表需要使用多少个左括号,如果最后count大于0了,就说明之前有多余的左括号还没有配对,需要在answer中加上,代表还需要添加多好个右括号
17:46 给定一个数组,求差值为k的去重数字对
比如[3,2,7,5,0]这样一个数组,需要找到所有差值为2的,且不能重复,那答案就是(3,5)(5,7)(0,2),做法就是把所有这些数都放到哈希表里,然后找当前数字+差值的数字存不存在,就能避免重复,利用哈希表的查询很节省时间,没有code
23:00 magic操作
29:00 开始讲解, 两集合平均值相等时无法magic,一个magic操作其实只能从平均值大的集合中拿数,拿到平均值小的集合中
40:00 code,累加和记为double类型,因为平均数可能是小数,但是要去的数肯定是整数
较大的集合排个序,这样方便找平均值,较小的集合用哈希表记录下来,搬运的时候需要保证小集合里没有这个数
———————————————————————————————————————————
中级提升班3
5:12 题目四
从左往右遍历遇到左括号就count++,遇到右括号就count--,count产生的最大值就是最大深度
9:07补充题目 有一个有左括号和右括号的字符串,找到最长的有序括号子串
20:35 举例说明如何用dp来求这个问题
code:24:17
26:43 题目五
使用一个辅助空间来存放栈顶元素,维护的另一个栈是从小到大排序的
30:43 题目三
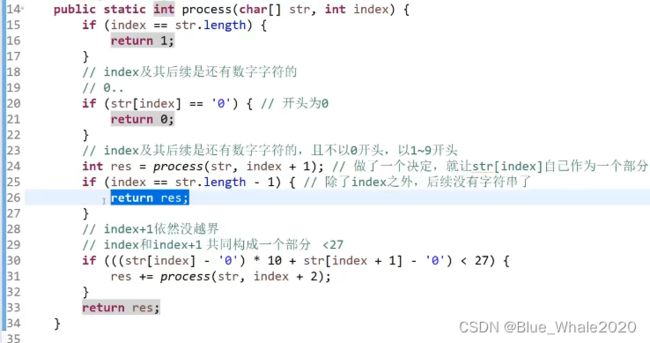
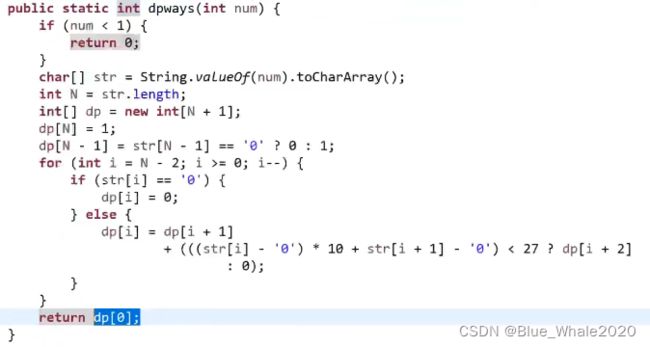
这是一个从左往右的尝试模型,F(I)代表从I位置开始,往后还有多少种可能,主函数在调用的时候直接返回F(0)就行了,
决策行为只有三种,当i位置是0时,没有办法转,可能结果是0,当i位置不是零,那么方法数是F(I+1),如果i位置和i+1位置之和小于26,那么还有一种方法数是F(I+2)
code:42:00
这个第26行代码是一个不好懂的地方,其实第26行和第33行的地址是相等的,他确定了整个大函数的返回时机,如果i位置已经来到了最后一个,后面没有i+1位置了(也就是25行的判断),那就返回res,如果还有后一个位置且小于26(30行的判断),那res需要类加上另一种可能才能返回
44:00 转动态规划表
46:30 题目七
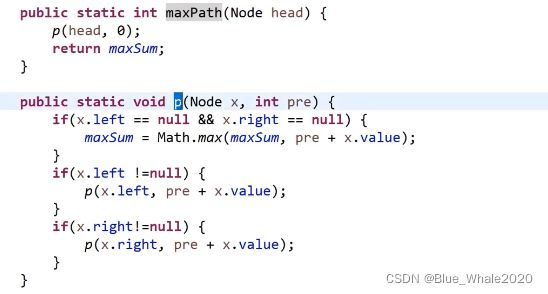
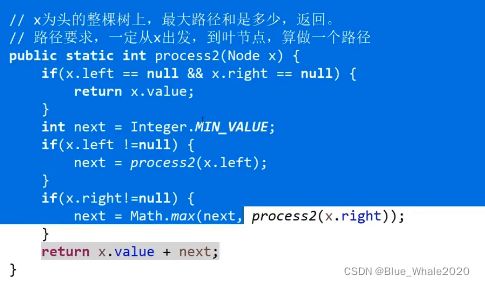
二叉树的每一个节点都有一个int型权值,给定一个二叉树,要求计算出从根节点到叶节点的所有路径中,权值和最大的值是多少
基础版的code,讲解在54:00
59:00 套路解
两个方法都可以
1:01 给定一个非负整数二维数组matrix,每行每列都是有序的,再给定一个非负整数aim,请判断aim是否再matrix中
最快的方式是从矩阵的右上角开始找,然后从右往左滑动,具体还是看视频吧,非常巧妙
变化形式,1:04:48,在一个二维数组中,只有0和1两种元素,且所有的0都在1的左边,返回含有1数量最多的行,做法还是从右上角开始走