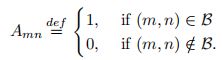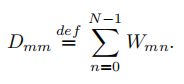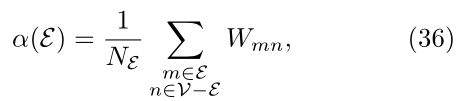Graph Signal Processing——Part I: Graphs, Graph Spectra, and Spectral Clustering （文献翻译）

 

目录

 

目录

0.Abstract

1.Introduction

2.图形定义和属性

2.1 基本定义

2.2 一些常用的图拓扑

2.3 图及其相关矩阵的性质

3.图矩阵的谱分解(特征分解)

3.1 邻接矩阵的特征值分解

3.1.1 特征及最小多项式的性质

3.2 谱图理论Spectral Graph Theory

3.2.1 DFT基本函数（离散傅里叶变换）是邻接矩阵特征向量的一种特殊情况

3.2.2 图积邻接矩阵的分解

3.2.3 矩阵幂和多项式的分解

3.3 拉普拉斯图的特征值分解

3.3.1 拉普拉斯特征值分解的性质

3.3.2 傅里叶分析是拉普拉斯谱的一个特例

4.顶点聚类与映射

4.1 基于图拓扑的聚类

4.1.1 最小切聚类算法

4.1.2 最大流量最小分割方法(Maximum-flow minimum-cut approach)

4.1.3 归一化(比率)最小切割

4.1.4 容量归一化最小切割

4.1.5 其他形式的归一化切割

4.2 图聚类的谱方法

---

注：vertices：翻译为顶点或节点

 

0.Abstract

图上的数据分析领域公认一种范式的转变，因为我们接近数据类的信息处理，这些数据通常是在不规则但结构化的领域(社交网络、各种自组织传感器网络)上获得的。然而，尽管历史悠久，目前的方法大多关注于图本身的优化，而不是直接推断学习策略，如检测、估计、统计和概率推理、从图上获取的信号和数据聚类和分离。为了填补这一空白，我们首先从数据分析的角度重新审视图拓扑，并通过图拓扑的线性代数形式(顶点、连接、指向性)建立图网络的分类。这作为图的光谱分析的基础，图拉普拉斯矩阵和邻接矩阵的特征值和特征向量被显示出来，以传达与图拓扑和高阶图属性相关的物理意义，如切割、步数、路径和邻域。通过一系列精心挑选的例子，我们证明了图的同构特性使基本属性和描述符在整个数据分析过程中得以保留，即使是在经典方法失败的图顶点重新排序的情况下。其次，为了说明对图信号的估计策略，通过对图的数学描述符的特征分析，以一般的方式介绍了图的谱分析。最后，建立了基于图谱表示(特征分析)的顶点聚类和图分割框架，说明了图在各种数据关联任务中的作用。支持的例子展示了图数据分析在建模结构和功能/语义推理中的前景。同时，第一部分是第二部分和第三部分的基础，第二部分论述了对图进行数据处理的理论、方法和应用，以及从数据中学习图拓扑。

特征分解（Eigendecomposition），又称谱分解（Spectral decomposition）是将矩阵分解为由其特征值和特征向量表示的矩阵之积的方法。需要注意只有对可对角化矩阵才可以施以特征分解。

https://baike.baidu.com/item/%E7%89%B9%E5%BE%81%E5%88%86%E8%A7%A3/12522621?fromtitle=%E8%B0%B1%E5%88%86%E8%A7%A3&fromid=19050835&fr=aladdin

1.Introduction

图信号处理是一个多学科的研究领域，其起源可以追溯到20世纪70年代[1,2,3]，但近年来迅速复苏。最近的发展，为了响应由全新类型的数据源提出的要求，通常是在不规则数据领域的图上的经典结果，以解决图上的信息和图上的信号的全新范式。这导致了先进的和有物理意义的解决方案在多方面的应用[4,5,6,7,8]。虽然图的新兴领域机器学习(GML)和图像信号处理(GSP)组成图形本身的经典优化方法(9、10、11、12、13、14、15),取得了重大进展重新定义基本数据分析范式(谱估计、概率推理、过滤、降维、集群、统计学习),让他们可以直接估计信号图(16、17、18、19、20、21,22,23,24，25,26]。事实上，在许多实际场景中，信号域不是由时间上的等距瞬时或是空间或变换域中的规则网格指定的，这是必要的。例子包括现代数据分析如社交网络建模或在智能电网数据域通常是不规则的,在某些情况下,甚至有关时间和空间的概念,在理想情况下,数据传感领域也应该反映的特定于域的属性考虑系统/网络;例如，在社交或网络相关的网络中，传感点及其连接性可能与特定的个人或主题有关，以及它们的链接，在不规则的域上处理，因此需要考虑数据属性，而不是时间或空间关系。此外，即使是在定义良好的时间和空间领域感知数据，通过图形引入的新的感知点之间的上下文和语义关系，有望使问题定义具有物理相关性，从而为分析和增强数据处理结果提供新的见解。在应用程序域的数据方便地定义为一个图表(社交网络、电网、车载网络、大脑连接),经典的时间/空间采样点的作用是由图的顶点（即节点，可观察数据值）来承担的,而顶点之间的边指定顶点连接的存在和性质(方向、强度)。这样，图就可以很好地利用测量数据和底层图拓扑之间的基本关系;这种整合物理相关数据属性的内在能力，使GSP和GML成为新兴大数据分析领域(BDA)的关键技术。事实上，在定义在不规则数据域上的应用中，图数据分析(Graph data Analytics, GDA)已经被证明是经典时间(或空间)序列分析中向前迈向量子领域的一步[27,28,29,30,31,32,33,34,35]，包括以下几个方面：
1)基于图形的数据处理方法不仅可以应用于技术、生物和社交网络，它们还可以改进现有技术，甚至在经典信号处理和机器学习方面创造出全新的方法
2)图表的参与使时间和空间的经典传感领域结构(也可以表示为一个线性或圆形图)以一个更高级的形式呈现,例如,通过从信号相似性或传感器关联的角度考虑感知点之间的连通性。

图数据分析的第一步是决定图作为一个新的信号/信息域的属性，然而，尽管数据感知点(图顶点)可能由应用本身很好地定义，但它们的连接性(边)却不是这样：
1）在各种计算机、社会、道路、交通和电力网络的情况下，顶点连通性通常是自然定义的，从而产生精确的底层图拓扑
2）在许多其他情况下，以图形形式定义的数据域成为问题定义本身的一部分，就像金融或智慧城市中的传感器网络的图形一样，在这种情况下，顶点连通性方案需要根据感知位置的特性或根据获得的数据来确定，例如在气象学中估计温度场

适当图结构定义的这一额外方面对于有意义和有效地应用GML和GSP方法至关重要。
考虑到这一点，本教程是为了响应多学科数据分析群体的迫切需求而编写的，这些群体需要从经典数据分析无缝地、严格地过渡到直接在不规则图域上运行的相应范式。为此，我们从回顾图的基本定义及其性质开始我们的方法，接着是物理直觉和图谱分析(特征分析)的逐步介绍。特别强调的是图矩阵的特征分解，它是图信号和信息处理的数学形式的基础。作为GML和GSP推广图的标准方法能力的一个例子，我们逐步地详细介绍了图离散傅里叶变换(GDFT)，并证明了它可以简化为有向圆图的标准离散傅里叶变换(DFT);这也说明了图方法的一般性质。最后，阐明谱顶点分析和谱图分割是理解图中不同但有物理意义区域之间关系的基础;这在区域基础设施建模、大脑连接、聚类和降维的例子中得到了演示。

2.图形定义和属性

图论作为数学的一个分支已经建立了近三个世纪，并已成为科学和工程领域的主要方法论，包括化学、运筹学、电气和土木工程、社会网络和计算机科学。图论在电气工程中的应用可以追溯到19世纪中期引入基尔霍夫定律。快进到两个世纪左右，从图上获得的数据分析已经成为信号处理和机器学习领域迅速发展的研究范式

2.1 基本定义

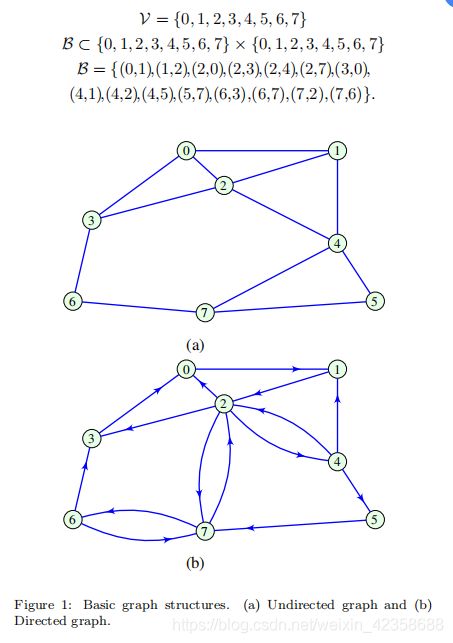
图G = {V, B}定义为一组由边B所连接而成的顶点V

• 定义:邻接矩阵的元素Amn，假设Amn∈{0,1}。如果顶点m和n不与边相连，则赋值Amn = 0，如果顶点m和n与边相连，则赋值Amn = 1，即

因此，相应的邻接矩阵Aun分别表示图1(a)和(b)中的无向图和有向图：

邻接矩阵不仅充分反映了数据采集的拓扑结构所产生的结构，而且承认了通常通过线性代数进行的特征分析，可以是稀疏的，也可以表现出其他一些有趣和有用的矩阵性质。

在矩阵中，若数值为0的元素数目远远多于非0元素的数目，并且非0元素分布没有规律时，则称该矩阵为稀疏矩阵；与之相反，若非0元素数目占大多数时，则称该矩阵为稠密矩阵。

注1:无向图的邻接矩阵是对称的
因为一个图完全由它的邻接矩阵（由给定的一组节点定义）决定，任何节点顺序的改变都会导致相应的邻接矩阵的改变。

注2:节点索引方案并不改变图本身(图是同构域)，所以原始图和重构图的邻接矩阵A1和A2之间的关系可用适当的置换矩阵P直接定义的，形式如下
回想一下，一个置换矩阵在每一行和每一列中都只有一个等于单位的非零元素（单位矩阵）。一般来说，通过加权图，这些边也可以传达关于它们连接的相对重要性的信息。

注3：权重矩阵W在形态上对应于边集B，因此一个有权图是一个无权图的一般扩展。通常假设边权是非负实数;因此，如果权值0与一条不存在的边相关联，则图可以用权值矩阵W来描述，类似于邻接矩阵A的描述。

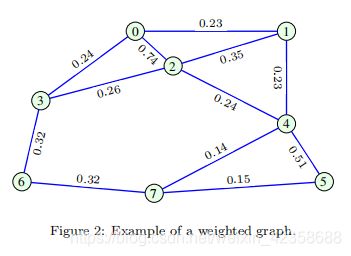
• 定义：权重矩阵W的元素Wmn指定顶点m和n之间的边和相应的权值，当Wmn = 0时，表示没有连接m和n顶点的边。且权矩阵W的元素为非负实数。图2给出了一个加权无向图的例子，其相应的权矩阵为：

在这个意义上，邻接矩阵A可以看作权值矩阵W的一种特殊情况，所有非零权值都等于一个单位。由此得出无向图的权矩阵也是对称的，但通常，对于有向图，此属性不成立。

• 定义：无向图的度矩阵D（degree matrix）是一个有元素的对角矩阵Dmm，它等于连接节点的所有边的权之和，即第m行元素的和

注4:对于无权无向图，元素Dmm的值等于与第m个顶点相连的边数。
节点度集中性Vertex degree centrality：节点的度集中性被定义为与该顶点相连的顶点的数量，通过这种方式它模拟了给定节点的重要性。对于无向无权图，一个节点的度集中性等于度矩阵的元素Dmm。
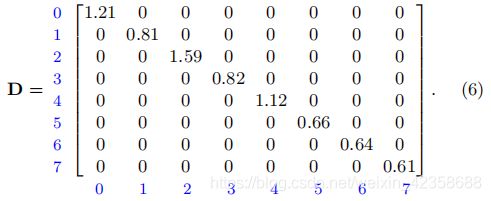
例1:对于图2中的无向加权图，度矩阵为

图连通的另一个重要描述符是图拉普拉斯矩阵L，它结合了权矩阵和度矩阵。

拉普拉斯矩阵的元素在对角线位置是非负实数，在非对角线位置是非正实数（负数或0）。
对于无向图，拉普拉斯矩阵是对称的，例如，图2中加权图的图拉普拉斯图矩阵为：

出于实际原因，使用归一化的拉普拉斯函数通常是有利的，定义为：

备注5:归一化拉普拉斯矩阵对于无向图是对称的，所有对角线值均为1，其迹等于节点数N。
通过拉普拉斯归一化得到的其他有趣的性质将在后面的应用中描述。
图拉普拉斯的另一种形式是所谓的随机游走拉普拉斯，定义为：

由于失去了原图的对称性，随机游走图的拉普拉斯图很少被使用

• 节点-权重图（Vertex-weighted graphs）：大部分的应用图论是基于edge-weighted图表,权重也可以引入vertex-weighted方法(尽管很少),即权重分配给每个节点的图。为此，我们可以使用一个对角矩阵V来定义节点权值vi,( i = 0,1，…， N-1），具有节点加权的图拉普拉斯的一个合理版本为：
  
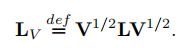
  当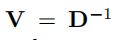时，该式可转化为（9）式

D=[1.21 0 0 0 0 0 0 0;0 0.81 0 0 0 0 0 0 ;0 0 1.59 0 0 0 0 0;0 0 0 0.82 0 0 0 0;0 0 0 0 1.12 0 0 0;0 0 0 0 0 0.66 0 0;0 0 0 0 0 0 0.64 0;0 0 0 0 0 0 0 0.61]
D_NI=inv(D)
W=[0 0.23 0.74 0.24 0 0 0 0;0.23 0 0.35 0 0.23 0 0 0;0.74 0.35 0 0.26 0.24 0 0 0;0.24 0 0.26 0 0 0 0.32 0;0 0.23 0.24 0 0 0.51 0 0.14;0 0 0 0 0.51 0 0 0.15;0 0 0 0.32 0 0 0 0.32;0 0 0 0 0.14 0.15 0.32 0]
L_N=D^(-1/2)*(D-W)*D^(-1/2)
L_RW=D_NI*(D-W)

------------------------------结果---------------------------------------
L_N =

    1.0000   -0.2323   -0.5335   -0.2409         0         0         0         0
   -0.2323    1.0000   -0.3084         0   -0.2415         0         0         0
   -0.5335   -0.3084    1.0000   -0.2277   -0.1798         0         0         0
   -0.2409         0   -0.2277    1.0000         0         0   -0.4417         0
         0   -0.2415   -0.1798         0    1.0000   -0.5932         0   -0.1694
         0         0         0         0   -0.5932    1.0000         0   -0.2364
         0         0         0   -0.4417         0         0    1.0000   -0.5121
         0         0         0         0   -0.1694   -0.2364   -0.5121    1.0000


L_RW =

    1.0000   -0.1901   -0.6116   -0.1983         0         0         0         0
   -0.2840    1.0000   -0.4321         0   -0.2840         0         0         0
   -0.4654   -0.2201    1.0000   -0.1635   -0.1509         0         0         0
   -0.2927         0   -0.3171    1.0000         0         0   -0.3902         0
         0   -0.2054   -0.2143         0    1.0000   -0.4554         0   -0.1250
         0         0         0         0   -0.7727    1.0000         0   -0.2273
         0         0         0   -0.5000         0         0    1.0000   -0.5000
         0         0         0         0   -0.2295   -0.2459   -0.5246    1.0000

2.2 一些常用的图拓扑

在处理图时，引入下列图拓扑分类是很有用的：
1)Complete graph:如果一个图的每一对顶点之间存在一条边，则该图是完备的。因此，对于所有m = n，完全图的邻接矩阵的元素Amn = 1，且Amm = 0，即不存在自连接。图3(a)给出了一个完全图的例子。
2)Bipartite graph:一个图，其图顶点V可以划分为两个不相交的子集E和H(V = E∪H, E∩H =∅),在同一个子集E或H内的顶点之间不存在边，称为二分图。图3(b)给出了E ={0,1,2}和H={3,4,5,6},所有边只表示集合E和H之间的连接。图3(b)中的图是一个完全二部图，其中，其邻接矩阵可以写成块矩阵的形式：

其中子矩阵AEH和AHE分别定义了属于集合E和h的顶点之间的连接。二分图也被称为Kuratowski图表,由表示，其中NE和NH表示各自集合的节点个数，特别强调的是，第一Kuratowski图可以用来定义一个图形是平面的条件
特例：多分图（多个节点集合）
3)Regular graph:如果一个无权图的所有节点都表现出相同的连通性(J)，则该图称为正则图(或J -正则图)。也就是说，连接到每个节点的边数都是是J。给出了正则图J = 4的一个例子图3 (c)。由(7)和(9)可知，J正则图的拉普拉斯行列式和规范化拉普拉斯行列式为：
   （即度矩阵D=JI）
4)Planar graph:能画在二维平面上而其各边不相交的图形称为平面图形。例如，如果图3(c)中的规则图中边(0,2)，(2,4)，(4,6)和(6,0)被绘制成由节点定义的圆外的拱形，所有的边交叉情况都将被避免，这样的图将是平面的
5)Star graph:这种图有一个中心顶点与所有其他顶点相连，没有其他边存在。图3(d)给出了星图的一个例子。观察到，一个星图可以看作是完全二部图的特例，在第一个集合e中只有一个顶点(即中心点为一个集合，其它点组成另外一个集合)。因此，一个有N个节点的星图，其中心节点的节点度集中性为n-1。
6)Circular graph:如果一个图的每个节点的度都是J = 2，那么这个图就是循环的。这个图也是J = 2的正则图。图3(e)给出了一个具有8个节点的循环图的例子。
7)Path graph:一系列连通顶点定义了一个路径图，其中第一个顶点和最后一个顶点的连通度为J = 1，其他顶点的连通度为J = 2。图3(f)给出了一个具有5个顶点的路径图的示例。
8)Directed circular graph:如果一个有向图的每个顶点只与一个前顶点和一个后继顶点相关，则说它是圆的。图3(g)给出了带有邻接矩阵的8个顶点的圆形有向图的一个例子。
注6:任何有向或无向圆图的邻接矩阵都是循环矩阵。
9)Directed path graph:有向路径图是由一个方向相连的一系列顶点定义的，其中第一个顶点和最后一个顶点没有各自的前身或后继顶点。图3(h)给出了一个具有5个顶点的有向路径图的例子。
注7:路径图和循环图(有向图和无向图)在数据分析中特别有趣，因为它们的域属性对应于经典的时间域或空间域。因此，任何为路径图和循环图开发的图信号处理或机器学习范式都等价于其相应的标准时间以及与或空间域范式。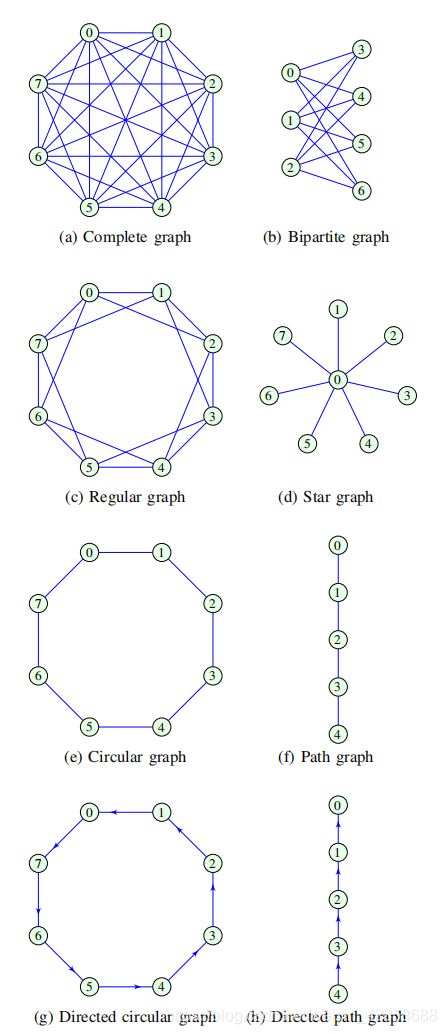
  FIGURE 3

2.3 图及其相关矩阵的性质

图分析中与图数据处理最相关的概念是:
1)对称:对于一个无向图，矩阵A、W、L都是对称的。
2)顶点m和顶点n之间的漫步是由顶点m开始到顶点n结束的边和顶点组成的连接序列。边和顶点可以包含在一次以上的漫步中。行走的长度等于无权图中包含的边的数目。从一个顶点m到一个顶点n，长度为K的行走次数等于矩阵第mn元素的值，可以通过数学归纳法证明，如下[46]:
(i)邻接矩阵A的元素Amn，根据定义，K = 1表示有一个长度的游走(图中顶点m和n之间的一条边);
(ii)假设矩阵的元素等于两个任意顶点m和n之间长度为k-1的步数;
(iii)m和n两个顶点之间长度为K的游走数量，等于节点m和过渡节点s两个顶点之间所有长度为K-1的游走数量，是由矩阵中ms位置的元素表示的，其是根据(ii)中的假设，对于所有顶点s，存在一条从s到目标节点n的边。如果过渡顶点s和最终顶点n之间存在一条边，那么Asn = 1。这意味着，两个顶点m和n之间的长度为K的游走数是的第m行与A的第n列的内积，可得的mn元素：

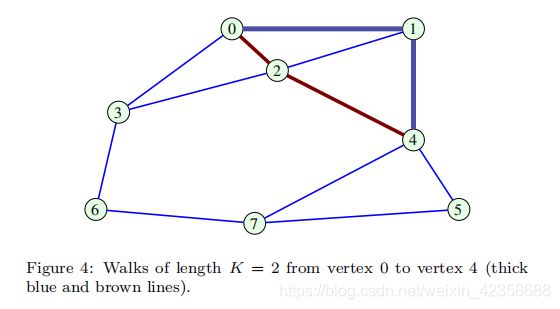
例子2：由图4可知，节点0和4的之间长度为2的游走数量为2（0 → 1 → 4 and 0 → 2 → 4），同理，所有节点的长度为2游走数量如下所示：

3)顶点m和n之间长度不大于K的游走数由下面矩阵的第mn个元素给出：

换句话说，行走的总次数等于所有行走的总和。
4)节点的K-neighborhood指的是该节点对应游走步长值为K的节点集合。基于（2）的性质，对于顶点m，其K-neighborhood由(16)中矩阵BK第m行非零元素的位置以及个数来指决定。K = 1和K = 2时顶点0的K-neighborhood如图5所示。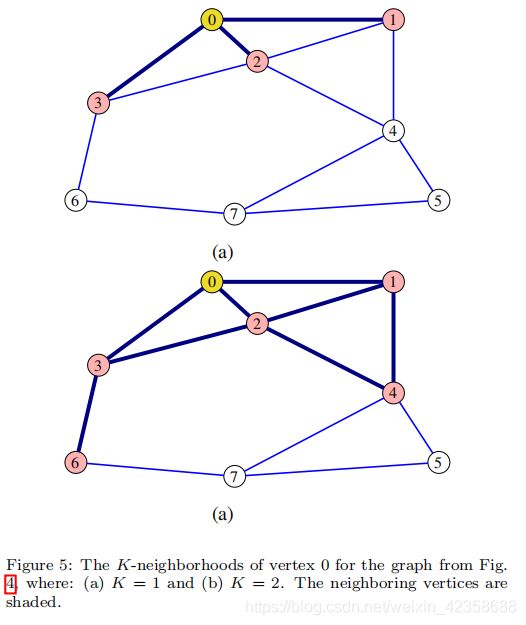

5）path是一种特殊的游走方式，其中每个顶点只能包含一次，而包含在路径中边的数量称为路径基数或路径长度(the path cardinality or path length)，路径权值定义为沿这些边的权值之和。
欧拉路径Euler path：如果图G中的一个路径包括每个边恰好一次，则该路径称为欧拉路径。一个无权图的欧拉路径确实存在当且仅当它的至多两个顶点是奇数次。
一个从同一个顶点开始和结束的欧拉路径称为欧拉回路，当且仅当每个顶点的度数都是偶数时它才存在。
哈密顿路径Hamiltonian path需要满足两个要求

• 每个顶点都要访问一次
• 能够回到初始顶点

6）distance：无权图中两个顶点m和n之间的距离rmn等于这两个顶点之间的最小路径长度。例如，在图4中，顶点1到顶点5的距离为r15 = 2。
7）diameter通径：图的通径d等于其顶点对之间的最大distance(边数)，即。例如，一个完整图的通径为d = 1，而图4中的图的通径为d = 3，其中一条最长distance为6→3→2→1。
8）Vertex closeness centrality节点紧密中心性：紧密中心性反应某一节点与其他节点之间的接近程度。如果一个节点离其他节点越近，那么他传播信息的时候也就越不需要依赖他人。一个节点到网络中各点的距离都很短，那么这个点就不会受制于其他点。点的紧密中心性是基于该节点到网络中其他所有节点的最短路径之和。其中，Cn越大，接近程度越高
                   
例如，图1(a)中n = 2和n = 5的顶点的距离和贴近度分别为f2 = 10, f5 = 14, c2 = 0.1, c5 = 0.071。
9）Vertex or edge betweenness：等于这个顶点/边在其他两个顶点之间的最短路径上充当桥梁的次数。
10）Spanning Tree and Minimum Spanning Tree.。一个图的生成树是一个子图，它是树形的，并把所有的顶点连接在一起。树没有周期，不能被断开连接。生成树的cost是树中所有边的权值之和。最小生成树是图的所有可能生成树中cost最小的一棵生成树。生成树通常用于图聚类分析。
在图论文献中，通常假设加权图的边权值与标准顶点距离rmn成正比。然而，在图上的数据分析中却不是这样，边的权值通常定义为顶点距离的函数，例如，通过高斯核，或其他一些数据相似度度量。最小生成树(MST)的最小代价函数可以定义为距离的和rmn = -2lnWmn。图2的生成树如图6所示。这个生成树的代价，作为所有距离(对数权重)的总和计算，rmn是15.67。

11)无向图的每一对顶点之间存在游走，则无向图是连通的。
12）如果图是不连通的，则它由两个或多个不相交但局部连通的子图(图分量)组成。回到数学形式，这样的不相交图产生了邻接矩阵A和拉普拉斯矩阵L的块对角线形式,对于一个图的M个不相交分量(子图)，这类矩阵的形式如下：

注意，这种块对角线形式只有在顶点编号遵循子图结构时才能获得。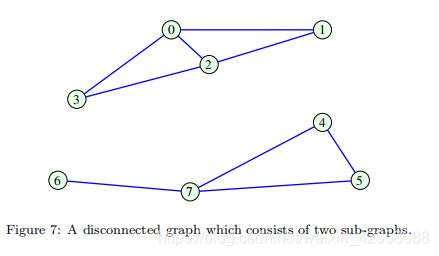

例3:图7所示图的邻接矩阵和相应的拉普拉斯函数为：

如上所述，这些矩阵采用块对角线形式，两个组成块清晰地分开。因此，对于图中的隔离顶点，A和L对应的矩阵的行和列都是零值。
13）定义在同一顶点集上的两个图，具有相应的邻接矩阵A1和A2，求和操作产生一个新的图，其邻接矩阵 A = A1 + A2
为了保持结果邻接矩阵中的二进制值Amn∈{0,1}，可以使用逻辑(布尔)求和规则进行矩阵加法，例如1 + 1 = 1。在本文中，在数据分析算法中假设算术求和规则，如属性(3)中的式(16)。
14)The Kronecker (tensor) product：两个分离的图G1 = (V1, B1)和G2 = (V2, B2)的克罗内克(张量)积产生一个新的图G = (V, B) ，其中：
i）V = V1×V2的是V1和V2的直接积,
ii）只有(n1,n2)∈B1和(m1, m2)∈B2,才有((n1, m1)，(n2, m2))∈B。图G的邻接矩阵A等于单独的邻接矩阵A1和A2的克罗内克乘积，即A = A1 ⊗ A2.
图8给出了两个简单图的克罗内克积的图解。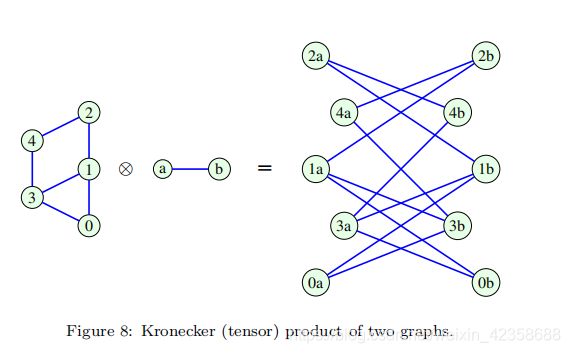

15）The Cartesian product (graph product)笛卡尔积(图积)：两个分离的图G1 = (V1, B1)和G2 = (V2, B2)的笛卡尔积(图积)产生一个新的图G = (V, B) ，其中：
i）V = V1×V2的是V1和V2的直接积,
ii）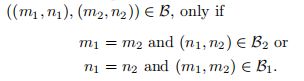

两个图的笛卡尔积的邻接矩阵A则由克罗内克积的和可以得出：

其中A1、A2分别为图G1、G2的邻接矩阵，N1、N2分别为图G1、G2中对应的顶点数，IN1、IN2分别为N1阶、N2阶的单位矩阵。两个简单图的笛卡尔积如图9所示。注意，对应于二维空间的两个图的笛卡尔积可以被认为是顶点和边的三维结构。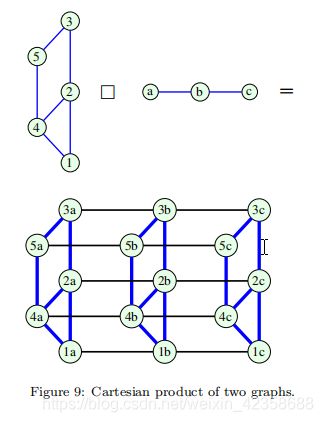

3.图矩阵的谱分解(特征分解)

作为对图进行优化和数据分析的先决条件，我们接下来将介绍线性代数工具和图拓扑之间的几个联系

3.1 邻接矩阵的特征值分解

像任何其他一般矩阵一样，图矩阵可以用特征值分解来分析。在这个意义上，如果Au = λu，则列向量u是邻接矩阵A的一个特征向量，与特征向量u相对应的常数λ称为特征值。
以上关系可以写成(A-λI)u = 0，u存在非平凡解的条件：det|A-λI|= 0.（非平凡解是齐次方程或齐次方程组的非零解）
换句话说，问题转化为寻找det|A-λI|的零点作为λ的一个多项式的根，称为矩阵A的特征多项式：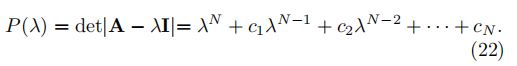

注8:图的特征多项式的阶数具有节点数N的物理意义，而特征值λ代表特征多项式的根，即P(λ)= 0。
一般来说，对于一个有N个顶点的图，其邻接矩阵有N个特征值，λ0，λ1，…,λN-1。某些特征值也可能是重复的，这表明在特征多项式中存在大于1的代数重数。一个特征多项式的根的总数，包括它们的重根数，必须等于它的次数N，因此
•特征值的代数重数λk，等于其作为特征多项式的重数;
•特征值的几何重数λk是与该特征值相关的线性无关特征向量的数目。
一个特征值的几何多重性(一个特征值的独立特征向量的数目)总是等于或低于其代数多重性。

1、几何重数：在矩阵bai运du算中，该矩阵有特征zhi值dao是重根，则该特征值所对应的特zhuan征向量所构成空间（即特征子空间，也是方程组(λI-A)x=0）的维数，称为几何重数。
2、代数重数：指方程的根的重数。

µ1, µ2, . . . ,µNm表示不同的特征值,及其对应的代数重数p1, p2,。， pNm，其中p1 +p2 +···+pNm = N等于所考虑的矩阵/多项式的阶数，Nm(≤N)是不同特征值的个数。特征多项式现在可以写成这样的形式: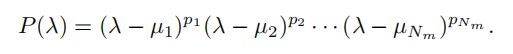

定义:通过将所有特征值的代数重数化为统一，得到邻接矩阵A的特征多项式的最小多项式，形式如下：

3.1.1 特征及最小多项式的性质

P1:特征多项式的阶数等于所考虑的图中顶点的个数。
P2:对于λ= 0,
P3:所有特征值的和等于邻接矩阵A的对角线元素的和，即其迹tr{A}。对于邻接矩阵P(λ)的特征多项式，即(22)中的c1值为c1 = tr{A} = 0。
P4:P(λ)的系数c2的等于边的数量乘以-1。这个属性，连同P3，从faddev - leverrier算法计算方阵a的特征多项式的系数，如c1 =- tr{A}， c2 = -1/2(tr{})，以此类推。由于tr{A} = 0和A2的对角线元素等于连接到每个顶点的边数(顶点度数)，所以边的总数等于tr{}/2 =-c2。
P5:最小多项式的次数Nm严格大于图通径(diameter)d。

例4:考虑一个有N个顶点且只有两个显著特征值λ0和λ1的连通图。那么最小多项式的阶为Nm = 2，而此图的通径为d = 1，表示为完全图。

例5:对于图1(a)中的图，其定义在(1)中邻接矩阵A的特征多项式为:
其特征值为：
在特征值不同的情况下，最小多项式等于特征多项式，Pmin(λ)= P(λ)。

例6:图7非连通图的邻接矩阵如式(19)所示，其特征多项式为：
，其特征值为：
λ ∈ {−1.5616,-1.4812, -1, -1, 0, 0.3111, 2.1701, 2.5616}.
观察到特征值λ=-1的重数大于1(重数为2)，因此相应的最小多项式变成：
​​​​​​
虽然该图是不连通的，但其邻接矩阵最大特征值λmax = 2.5616的重数为1。图的连通性与特征值的多重性之间的关系将在后面讨论。

3.2 谱图理论Spectral Graph Theory

如果A的所有特征值都是不同的(代数重数为1)，则(21)中特征值问题的N个等式，即，可以写成一个关于邻接矩阵的紧凑的矩阵方程：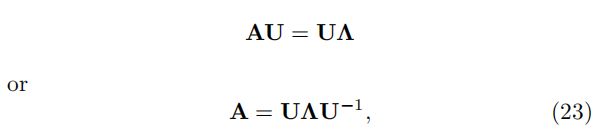

其中Λ= diag(λ0，λ1，…，λN-1)是一个对角线矩阵，其对角线上有特征值，而U是一个由特征向量uk作为其列组成的矩阵。由于特征向量u是通过求解由(21)定义的齐次方程组得到的，其形式为(A-λI)u = 0，特征向量u的一个元素可以任意选择。通常的选择是强制uk的L2范式的平方 
 

备注9:对于无向图，邻接矩阵A是对称的
对于任何对称矩阵：(i)都有实数特征值;(2)对角化的;(iii)有正交的特征向量，因此

注10:对于有向图，一般。
回顾一下，如果方阵的所有特征值都是不同的(这个条件是充分的，但不是必要的)，或者每个特征值的代数多重性与其几何多重性相等，那么方阵是可以对角化的。
对于某些有向图，其邻接矩阵的特征值代数重数大于1时，矩阵A可能不能对角化。在这种情况下，所考虑的特征值的代数多重性高于其几何多重性，可以使用约当范式。

定义:邻接矩阵特征值的集合称为图邻接谱graph adjacency spectrum。
注11:图的谱理论通过图的邻接关系的特征值和特征向量以及图的拉普拉斯矩阵来研究图的性质。
示例7:图1 (a)中给出的图,这个图邻接谱是根据λ∈{−2,-1.741,-1.285,-0.677,0.411,1.114,1.809,3.190},如图10所示(top)。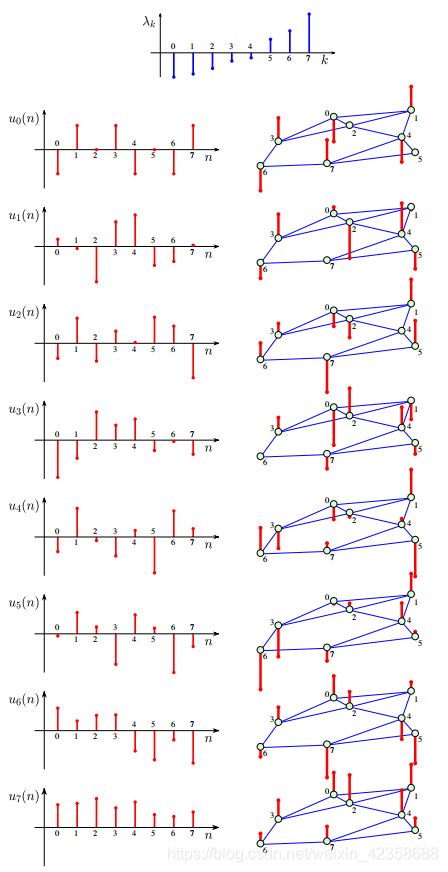

图10 展示了对于图1(A)所示无向图的邻接矩阵A特征值λk（谱指数(特征值数)k = 0,1，…， N-1），以及对应特征向量的元素uk(N)（顶点索引N = 0,1，…， N-1）。在顶点索引轴n(左)和图(右)上显示了不同的特征向量。

求式（1）A的特征向量和特征值
matlab代码：

A=[0,1,1,1,0,0,0,0;1,0,1,0,1,0,0,0;1,1,0,1,1,0,0,0;1,0,1,0,0,0,1,0;0,1,1,0,0,1,0,1;0,0,0,0,1,0,0,1;0,0,0,1,0,0,0,1;0,0,0,0,1,1,1,0]
[U,lamda]=eig(A) %求矩阵A的特征值和特征向量,其中lamda的对角线元素是特征值,其中U的X的列是相应的特征向量,

结果：
A =

     0     1     1     1     0     0     0     0
     1     0     1     0     1     0     0     0
     1     1     0     1     1     0     0     0
     1     0     1     0     0     0     1     0
     0     1     1     0     0     1     0     1
     0     0     0     0     1     0     0     1
     0     0     0     1     0     0     0     1
     0     0     0     0     1     1     1     0


U =

    0.4082    0.1232   -0.2563    0.6294    0.2478   -0.0357   -0.3811    0.3852
   -0.4082   -0.0341    0.4241    0.3062   -0.4845    0.3604   -0.1634    0.4089
    0.0000   -0.5981   -0.3015   -0.4786    0.0612    0.1162   -0.2586    0.4881
   -0.4082    0.4178    0.2068   -0.2536    0.3215   -0.5164   -0.2672    0.3320
    0.4082    0.5342    0.0129   -0.3581   -0.1099    0.3212    0.3441    0.4311
    0.0000   -0.3192    0.4430    0.1752    0.6086    0.0958    0.4944    0.2171
    0.4082   -0.2523    0.2921    0.0208   -0.4411   -0.6559    0.1563    0.1860
   -0.4082    0.0214   -0.5822    0.2396   -0.1402   -0.2145    0.5500    0.2615


lamda =

   -2.0000         0         0         0         0         0         0         0
         0   -1.7407         0         0         0         0         0         0
         0         0   -1.2850         0         0         0         0         0
         0         0         0   -0.6768         0         0         0         0
         0         0         0         0   -0.4109         0         0         0
         0         0         0         0         0    1.1143         0         0
         0         0         0         0         0         0    1.8086         0
         0         0         0         0         0         0         0    3.1905

例8:将图1(a)图中的顶点随机重新排序([0, 1, 2, 3, 4, 5, 6, 7] → [3, 2, 4, 5, 1, 0, 6, 7].)，如图11所示。观察在同一图中给出的图邻接谱保持相同的值，特征向量的顶点索引以与图顶点相同的方式重新排序，而特征值(谱)保持与原始图10相同的顺序
通过一个简单的检查，我们可以看到，例如，图10中n = 0的顶点索引位置的特征向量元素现在在图11中的n = 3的顶点索引位置。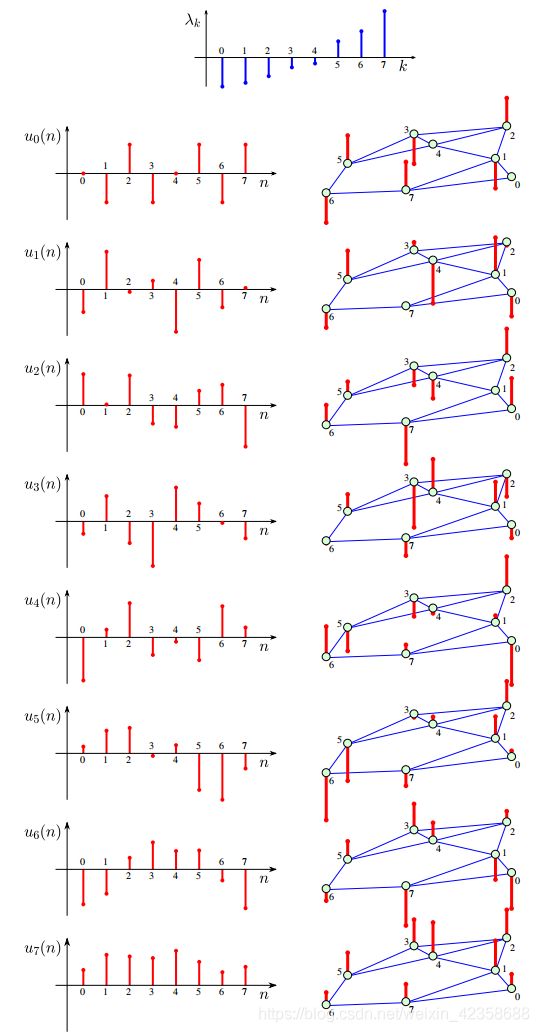

        图11
注12:图的一个独特特征是，重建顶点不会改变邻接矩阵的特征值，重建后的邻接矩阵的特征向量所包含的元素与原特征向量相同，只是按照顶点重编号进行了重新排序。这是由排列矩阵的性质得出的，如关系式(3)(即改变顶点索引方案并不改变图本身(图是同构域)，所以原始图和重述图的邻接矩阵之间的关系是用适当的排列矩阵P直接定义的)

3.2.1 DFT基本函数（离散傅里叶变换）是邻接矩阵特征向量的一种特殊情况

为了连续性的标准谱分析，我们将首先考虑有向圆，因为这种图拓扑可编译为标准的时间和空间域。
图3(g)中有向圆图的特征值分解，假设有N个顶点，根据定义和(14)中邻接矩阵的形式。当向量的元素为，则向量的元素为，即

其中uk(n)为给定顶点指标n = 0,1,...,N−1时特征向量uk的元素;k为特征向量(对应特征值)的指标，k = 0,1,...,N−1。这是一个一阶线性差分方程，其离散信号x(n)的一般形式为x(n) = ax(n−1)，其解为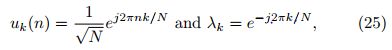

当k = 0,1,...,N−1时，证明该解满足差分方程(24)很简单。由于图是循环的，特征向量也表现出循环的特性，即uk(n) = uk(n+1)。为方便起见，利用单位能量条件unit energy condition 求出一阶线性差分方程通解内的常数。观察(25)中的特征向量完全对应于标准DFT谐波基函数。

DFT：https://blog.csdn.net/qq_39521554/article/details/79899225

备注13:当考虑有向圆图时，经典的DFT分析可以作为(25)中图谱分析的特例得到。可以看到，对于循环图，如（24），邻接矩阵A起着移位算子的作用（行列初等变换，“左行右列”），Auk的元素为uk(n−1)。在下面的章节中，此属性将用于在图形上定义移位操作符。

3.2.2 图积邻接矩阵的分解

我们已经在图8和图9中看到，复杂的图，例如具有三维节点空间的图，可以由两个不相交的图G1和G2的克罗内克(张量)积或笛卡尔(图)积得到。各自的邻接矩阵,A1和A2,应用到生成克罗内克图的邻接矩阵A⊗= A1⊗A2和笛卡尔图积A⊕= A1⊕A2。
对于矩阵A1和A2的克罗内克乘积的特征分解，以下是成立的：

换句话说,克罗内克积图的邻接矩阵的特征向量可由单个图的邻接矩阵的特征向量进行克罗内克积得到，如：

注14:单个图邻接矩阵的特征向量的维数远低于生成的图Kronecker积的邻接矩阵的维数。在分析这类图上观察到的数据时，可以使用此属性来降低计算复杂度。得到的图邻接矩阵的特征值等于组成图G1和G2邻接矩阵特征值的乘积，即:

图的笛卡尔积对应邻接矩阵分别为A1和A2，其特征分解为：


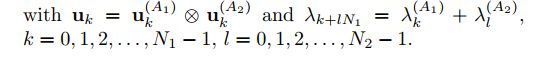
注15:图的克罗内克积和笛卡尔积在邻接矩阵中具有相同的特征向量，但其谱(特征值)不同(前者为积，后者为和)。

例9:经典的二维基函数(图像)2D-DFT是通过对图3中循环有向图与自身乘积的笛卡尔图乘积的光谱分析得出的。由(25)可知，每个图的特征向量元素为，则所得基函数的特征向量元素为：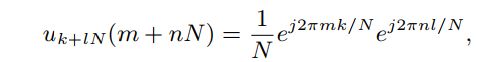

其中，k =0,1,...,N−1,l = 0,1,...,N−1,m =0,1,...,N−1，n= 0,1,...,N−1。
图12说明了N1 = N2 = 8时两个循环图的笛卡尔积：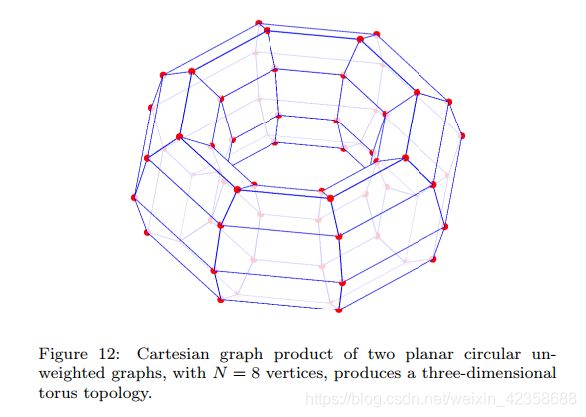

注16:图的笛卡尔积可以用于节点空间和图数据域的多维扩展，利用原图的低维特征向量可以有效地计算得到的特征向量(基函数)。

3.2.3 矩阵幂和多项式的分解

从特征分解的邻接矩阵(23)中，可以得出邻接矩阵的平方的特征值分解为：

同理：
进一步，对于任何矩阵函数，f(A)可以写成多项式形式：

其特征值分解一般为：
上式根据(26)中定义的矩阵幂的特征分解的性质，以及矩阵乘法算子的线性可得出

3.3 拉普拉斯图的特征值分解

谱分析的图形也可以执行定义在(7)的基于图拉普拉斯算子L。尽管拉普拉斯算子的特征值和特征向量并不直接相关，但为方便起见,我们这里采用相同的符号表示拉普拉斯算子的特征值和特征向量,就处理邻接矩阵A一样。因此，无向图的拉普拉斯图可以写成

其中，Λ= diag(λ0,λ1,...,λN−1)是一个具有拉普拉斯特征值的对角矩阵，U是其特征向量(列)的标准正交矩阵。注意无向图的拉普拉斯矩阵总是可对角化的，因为L是一个实对称矩阵,则拉普拉斯每个特征向量uk, (k = 0,1,...,N-1)满足:

定义:特征值的集合λk, k = 0,1,...,N−1,被称为是图谱或图的拉普拉斯谱(参考图的邻接谱A)。

例10:图2中无向图的拉普拉斯谱为：，其对应的特征向量展示在图13中
图14的无连接图的拉普拉斯谱为：如图15所示。无连接图的特点是有代数重数为2的零特征值，即λ0 =λ1 = 0。
备注17:注意，当使用基于图组件(子图)的节点索引时，即使图13连通图的图谱和未连接图15的图谱是相似的，但无连接图的给定谱指数的特征向量只无连接图分图中的一个有非零值。（即A1或A2中其中一个有非零值，另外一个全是零值，从图15可以看出）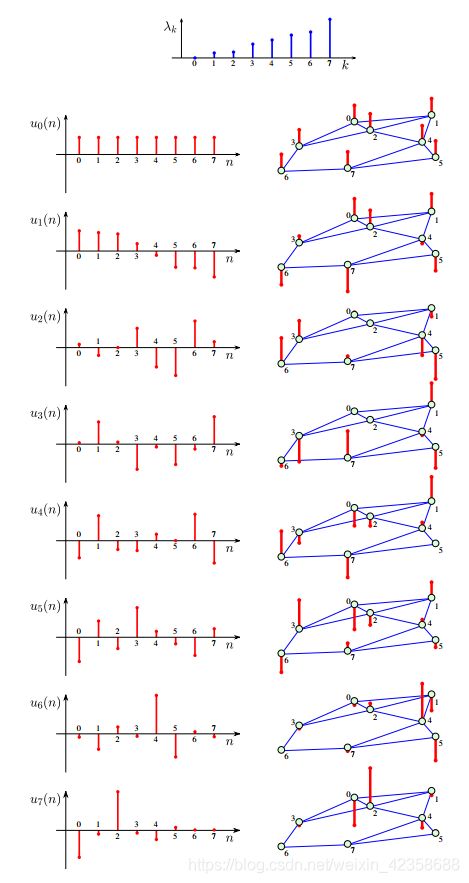

图13 与图10中邻接矩阵的特征向量比较可以看出，对于邻接矩阵A(图10)，其最光滑（特征向量同方向，大概同值）的特征向量对应最大的特征值，而对于图拉普拉斯矩阵L(图13)，其最光滑的特征向量对应最小的特征值λ0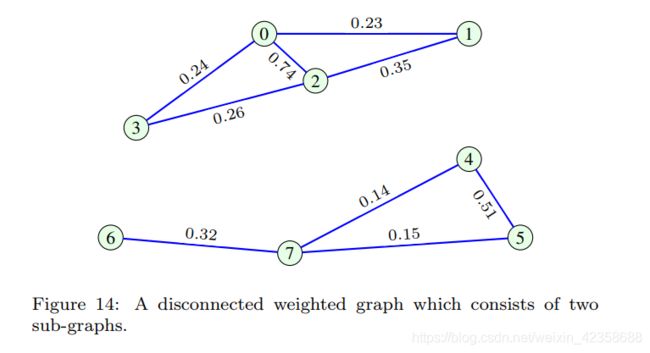


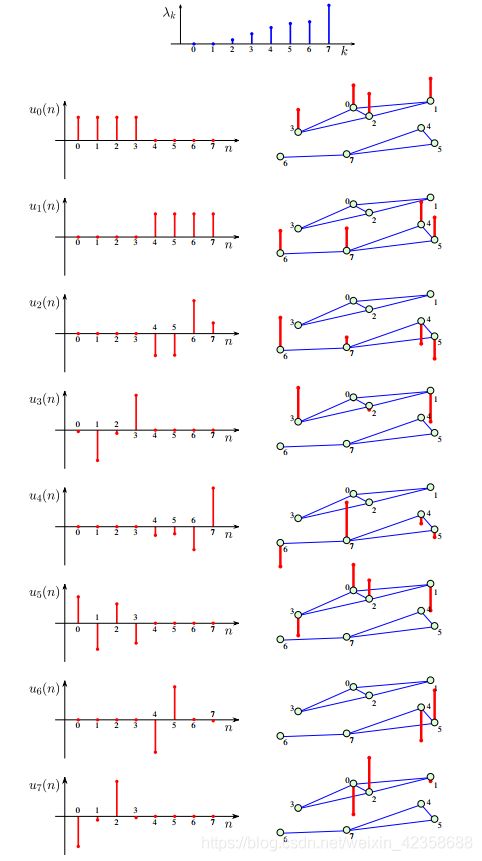
图15 该图具有代数重数为2的零特征值，即λ0 =λ1 = 0。可以看出，特征向量只在一子图上取非零值

3.3.1 拉普拉斯特征值分解的性质

L1:在(7)中定义的拉普拉斯矩阵L，其每一行(列)的元素之和为零。因此,这使得L与任何常数向量u的内积为0,即L u = 0 = 0·u。这意味着至少一个拉普拉斯算子的特征值是零,λ0 = 0,其相应的常数单位特征向量为：

L2:拉普拉斯矩阵的特征值λ0 = 0的重数等于对应图中连通分量(连通子图)的数目。（从图15可以看出，λ0=λ1=0，代数重数为2，有两个非连通子图）
这个性质源于这样一个事实，即不连通图的拉普拉斯矩阵可以写成块对角线形式，如(18)。块对角线矩阵的特征向量集是通过将各个块子矩阵的特征向量集组合在一起而得到的。由于不连通图的每个子图都表现为一个独立的图，那么根据L1的性质，对于每个子图λ0 = 0是对应块拉普拉斯子矩阵的特征值。（即每个子图的拉普拉斯矩阵都有一个零特征值）因此，特征值λ0 = 0的重数对应于不相交分量(子图)的个数。
这个性质不适用于邻接矩阵，因为在块(子图)或任意图的邻接矩阵中没有共同的特征值。在这个意义上，图拉普拉斯矩阵比相应的邻接矩阵具有更多的物理意义。
注18:如果λ0 =λ1 = 0，则图是不连通的。如果λ2 > 0，那么在这个图中正好有两个独立连接但全局不连通的子图。如果λ1≠ 0，那么这个特征值可以用来描述一个图的所谓代数连通性，λ1非常小的值表明这个图是弱连通的（接近0）。这可以作为图分割可能性的一个指标，如4.2.3节所述。

L3:和其他任何矩阵一样，拉普拉斯矩阵的特征值数和等于它的迹。对于标准化拉普拉斯矩阵，如果没有孤立的顶点，其特征值的总数等于顶点的数目N。

L4:图拉普拉斯矩阵的特征多项式中的系数Cn：
P(λ)= 0，因为λ= 0是拉普拉斯算子的特征值。
对于未加权图，系数c1等于边数乘以−2。根据属性P4的关系，这很容易说明c1 =−tr{L}。对于无权图，拉普拉斯行列式的对角线元素等于相应的顶点度数(边数)。因此，无权图的边数等于−c1/2。

例11:图1(a)图的拉普拉斯多项式的特征多项式为：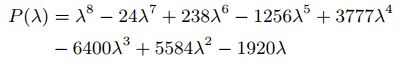

特征值λ∈{0,5.5616,5;4,4,3,1,1}。观察到λ= 1和λ= 4的特征值的重数大于1。最小多项式因此变成:

对于图7中的不连通图，拉普拉斯函数的特征多项式为:

特征值λ∈{0,0,1,2,3,4,4,4}。特征值λ= 0为代数重数为2，特征值λ= 4为代数重数为3，因此最小多项式为：

因为λ= 0的特征值具有代数重性为2（性质L2表示这个图是不连通的），有两个不连通的子图作为它的组成部分
L5:具有相同谱的图称为等谱图或共谱图。然而，等谱图不一定是同构的，非同构的等谱图的构造是图论中的一个重要课题。
注19:完全图是由其拉普拉斯谱唯一确定的。具有N个节点的完全无权图的拉普拉斯谱是λ∈{0,N,N,...,N}。因此，两个完全的等谱图也是同构的

图的同构：https://www.jianshu.com/p/c33b5d1b4cd9    简而言之同构图的邻接矩阵A相同

L6:对于J-正则图，如图3(c)所示，拉普拉斯矩阵和邻接矩阵的特征向量是相同的，而特征值的关系如下（上标L为拉普拉斯矩阵，上标A为相应的邻接矩阵）:

也可以写成：

L7:标准化拉普拉斯矩阵的特征值是非负和有上限的：
当且仅当图是二部图时，如图3(b)所示，上面的不等式等号成立。这将在下一个性质中得到证明

L8:归一化后具有不相交顶点集合E和H的二部图的拉普拉斯特征值和特征向量满足图谱折叠的关系：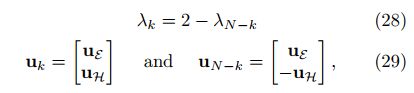

其中Uk为二部图的第k个特征向量，UE为Uk在第一组顶点E上的索引部分，UH为特征向量Uk在第二组顶点H上的索引部分。
为了证明这个性质，我们将无向二部图的邻接矩阵和标准化拉普拉斯矩阵写成块形式: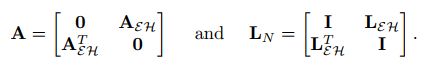

特征值的关系,现在可以写为：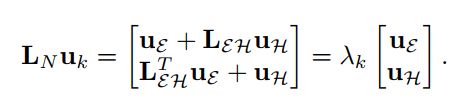


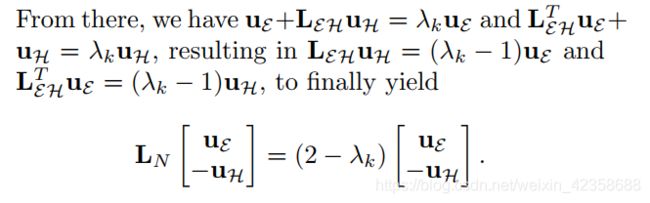
因为对于图来说，λ0 = 0总是成立的(参见性质L1)，由(28)可知，最大特征值是λN = 2，这也证明了二部图的性质L7

3.3.2 傅里叶分析是拉普拉斯谱的一个特例

考虑图3(e)中的无向循环图。然后，根据L1的性质，该图的拉普拉斯矩阵的特征分解关系Lu =λu可以有一个简单的形式：

通过求取图3(e)中的无向循环图的拉普拉斯L可以很容易地说明(30),假设N = 8个顶点，特征值分析可以得出：

(30)中二阶差分方程的解是
显然，对于每个特征值λk(除了λ0和最后一个特征值λN−1，对于一个偶数的N),我们可以选择两个正交的特征向量(例如φk = 0，φk =π/2)。这意味着大多数特征值的代数重数为2，即:λ1 =λ2，λ3 =λ4，以此类推。特征值的代数重数为2可以正式表示为：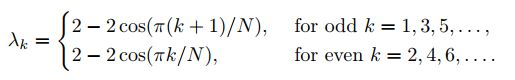

对于一个奇数的N，λN−2 =λN−1；而对于一个偶数的N，我们有λN−1 = 2，其代数多重数为1。
对应的特征向量形式为：

回顾一下,一个u2k−1和u2k（1 ≤ k ≤ N/2）特征向量的任意线性组合也是一个特征向量，因为对应的特征值是相等的(在这种情况下他们的代数和几何重数都等于2)。鉴于此,我们可以把全套的特征向量在另一个紧凑的形式给出：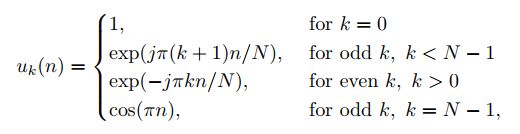

其中。很明显，正如所期望的那样，这组特征向量是标准正交的，每个特征向量uk对应于标准时空DFT中的标准调和基函数。

4.顶点聚类与映射

定义:顶点聚类是一种图学习方法，它的目的是将集合V中的顶点分组成多个不相交的子集，称为聚类( clusters)。被聚集成顶点子集的顶点Vi，被期望比其他子集中的顶点Vj有更大程度的群内相互相似(在某种意义上)。
图的聚类是指识别以及将节点放置不重叠子集的过程，使得每个子集的节点数据在某种意义上呈现相似性，图的分割是指将图划分为子图(组件)。
顶点相似性度量的概念及其用于相应地将顶点聚为图中的“相关”顶点集的使用，一直是机器学习和模式识别领域重要研究工作的焦点;这导致建立了许多用于图聚类[49]的顶点相似度量和相应的方法。这可以分为两大类:(i)基于图拓扑的聚类方法和(ii)基于光谱(特征向量)的图聚类方法。
注意，在传统的聚类中，一个顶点只在一个聚类中。一个顶点可能属于多个聚类的聚类类型被称为模糊聚类fuzzy clustering[49,50]，这种方法在图领域中还没有被广泛接受

4.1 基于图拓扑的聚类

在现有的许多方法中，最常见的是基于以下方法:
•以某种“最优”的方式找到断开图形连接的最小边集(基于最小切聚类算法)。
•根据图中最短路径数量最多的顶点或边(基于节点和边的聚类)来进行聚类。
•图的最小生成树是许多广泛使用的聚类方法的基础(51,52)。
•高连接子图[53]的分析也被用于图聚类。
•最后，图数据分析可以用于机器学习图聚类，例如，基于k-means的聚类方法[54,55]。

4.1.1 最小切聚类算法

我们将首先简要回顾图割的概念，因为图聚类的谱方法可以在(基于图拓扑的)最小割聚类的分析和近似的基础上引入和解释。
定义:考虑一个无向图由一组的顶点V和相应的边权重w构成, .假定一个顶点集分为k = 2的两个不相交的子集E和H。对于给定的顶点的子集E和H，这个图的切割，等于连接E和H这两个子集之间顶点的边的所有权值之和：

备注20:为了简单起见，我们将重点讨论顶点的k = 2个不相交子集的情况。然而，该分析可以直接推广到k≥2个不相交的顶点子集及其对应的最小k切。

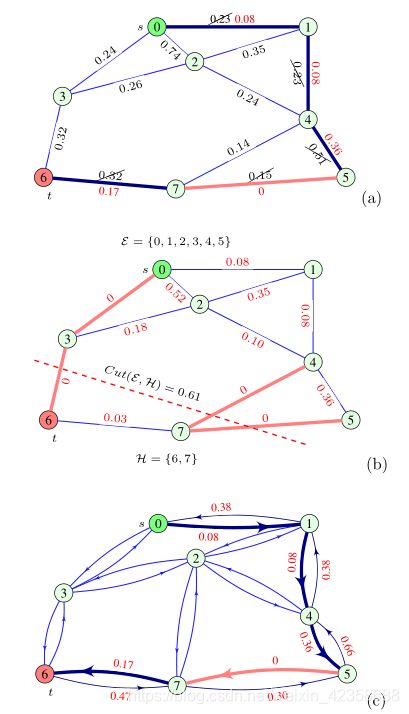
例12 图2有两个节点子集E ={0,1,2,3}和H = {4,5,6,7}，现将其分割为两个子图，两个子图存在联系的节点的边权重（图16红色线）之和为：cut(E,H) = 0.32+0.24+0.23 = 0.79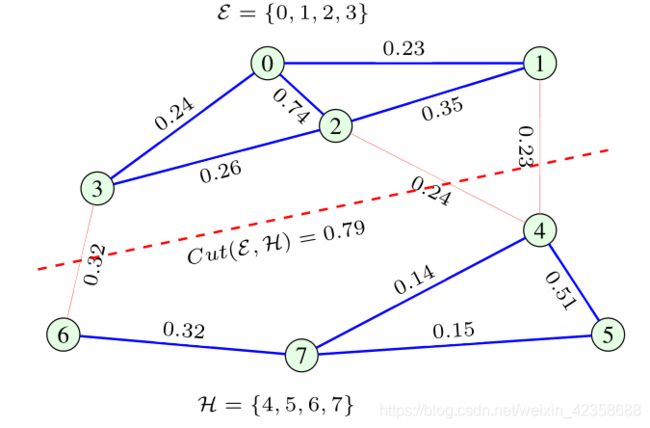

          图16 

定义:考虑到顶点集合V的所有可能划分，一个不相交子集E和H的权值之和最小的切割cut称为最小切割。用这种方法求图的最小分割是一个组合问题。
备注21:将一个偶数的N个顶点分裂成两个不相交的子集的所有可能组合的数目为(A排列)：

即使是一个N = 50个顶点的相对较小的图，将顶点分割成两个子集的组合数是C = 5.6·10^14,因此计算量特别巨大
例13 对于图16的图而言，最小分割为E ={0,1,2,3,4,5}和H = {6,7}，其cut=0.61，同时，8个节点分为两个子集共有127种可能，利用Stoer-Wagner algorithm也可找到最小分割

4.1.2 最大流量最小分割方法(Maximum-flow minimum-cut approach)

这种求解最小割问题的方法采用了流网络flow networks的框架。
定义:一个流网络是一个有向图，有两个给定的顶点(节点)，即源顶点s(the source vertex)和汇聚顶点t (the sink vertex)，其中边(弧)的容量由它们的权值定义。通过一条边的流量(信息，水，交通，…)不能超过其容量(边权值)。对于图中的任何顶点，所有输入流的总和等于所有输出流的总和(除了源顶点和汇聚顶点)
问题公式化。图划分的最大流量最小割解的目标是找到从源顶点s到汇聚顶点t的最大流量。该解决方案是基于最大流量最小割定理，说明最大流量从一个给定的源顶点s到一个给定的汇聚顶点 t，等于最小割值，也就是那些边权值(容量)的最小和，如果去掉，将断开源s和汇t(最小割容量)的连接。这个定理的物理解释是显而易见的，因为最大流量自然是由源和汇之间的图流容量瓶颈定义的。容量瓶颈(最大可能流)将等于最低容量(最低权值)的边,如果删除,将图分为两部分,一个包含顶点s,另包含顶点t。因此,最大流量的问题相当于最小分割的问题,在考虑s和t必须属于不相交的顶点子集E和H .这种带有预定义的顶点s和t的切割称为(s,t)切割。
备注22:一般来说，如果没有给出源顶点和汇聚顶点，应对所有源顶点和汇聚顶点的组合重复使用最大流量算法，以找到图的最小割。求解最小切最大流量问题最常用的方法是 the Ford–Fulkerson method

例14 Ford-Fulkerson方法是基于源和汇顶点之间的路径和对应流的分析。假设图2有权图的原点和汇聚点为s=0和t=6，一种可能存在的路径为0 → 1 → 4 → 5 → 7 → 6，如图17a实线所示。回顾一下，对于连接顶点s = 0和t = 6的路径，最大流量受到最小容量的限制(等于最小权值)。因此，对于考虑的路径0→1→4→5→7→6，从s = 0到t = 6的最大流量为：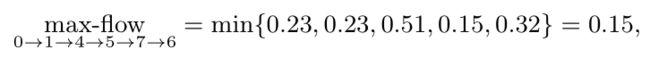

因为沿着这条路径的最小权值是连接顶点5和7的，所以W57 = 0.15。然后，最大流量的值从考虑的路径中的每个容量(权重)中减去最小容量0.15，新的剩余边缘容量(权重)在图17(a)的剩余图中用红色数字表示。重复相同的步骤重新挖掘可能路径0→3→6，0→2→4→7→6以及0→2→3→6后（3条路径都走了一遍，并在上一条路径的基础上做残差），在考虑每条路径后，对容量(边权值)进行适当的修正。如图17b所示，图的最终残差形式在以这样一种方式获得零容量边后，从s到t的非零流量的新路径就不能被定义。例如，如果我们考虑路径0→1→2→3→6(或任何其他路径)，残差图中，则其最大流量为0，因为边3→6的残差权值为0。现在，通过剩余的零容量(零权)边，我们得到了将汇聚顶点t = 6及其邻域与源顶点s = 0分离的最小切割。该切割如图17(b)所示，通过切割顶点3→6,4→7，5→7的连接边，将顶点H ={6,7}与其他顶点分。将这些边的原始总权值cut(E,H)= 0.32 + 0.14 + 0.15 = 0.61。
我们目前关注的是一个无向图,但自从Ford-Fulkerson算法通常用于有向图,注意到一个无向图可以被认为是一个有向图，只要每条边被分成两个拥有相同的权重但方向相反的边。在一个方向上(例如图17(a)中的边5-7)，在考虑的方向上流量等于其最大流量0.15后，另一个方向(姐妹边)变成0.30，如图17(c)所示。可以使用相反方向的边(两个方向的流量的代数和等于边的总容量)形成另一条从源到汇聚顶点的路径(如果可能的话)。更具体地说,假定方向上的边容量减少考虑流的值,而方向相反的另外一边增加了相同的流量,并且可以用来在相反方向发送流。图17(a)中路径的所有剩余容量均由图17(c)给出。为了清晰起见，图17(c)中没有显示

未被此流改变的边权值。

图17

4.1.3 归一化(比率)最小切割

可以使用许多优化方法来加强图聚类的一些期望属性。其中一种方法是图论中常用的归一化最小割，它是通过将cut(E,H)的值加上额外的项(代价)来使子集E和H同时尽可能大而引入的。归一化切割的一种显著形式(比率切割)如下：

NE和NH分别是E和H集合中顶点的个数，因NE+NH=N,所以当NE=NH=N/2时，(1/NE+1/NH)最小

例15 回顾例12和图16的图，对于顶点集E = {0,1,2,3}， H ={4、5、6、7},归一化切割计算为CutN(E,H) =(1/4 + 1/4) *0.79 = 0.395。这个切割也表示这个图的最小归一化切割;这可以通过检查这个(小)图中E和H的所有可能的切割组合来证实。图18显示了基于最小归一化切割的顶点聚类。但是，请注意，一般来说，最小切割和最小归一化切割不会产生E和H相同的顶点聚类。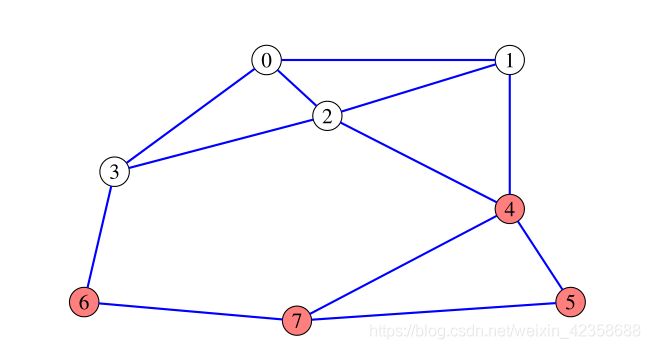

图18

4.1.4 容量归一化最小切割

在设计子集E、H的大小时，一个更一般的归一化切割形式也可能涉及顶点权值。通过分别定义这些集合的容量用这些容量来代替顶点的数量，在(33)中标准化切割的定义中，我们经过改进得到：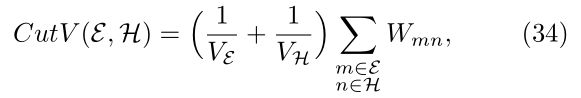

具有较高度的顶点被认为在结构上比具有较低度的顶点更重要。
以上讨论表明，寻找归一化最小割也是一个组合问题，对于这个问题，将在本节稍后讨论基于谱的近似解。

4.1.5 其他形式的归一化切割

除了两种基于顶点的数量和体积的标准切割，其他常用的形式在现有文献中包括:
1.切割的稀疏性，如下定义

其中V−E是V与E的集合差。切割的稀疏性ρ(E)与归一化切割有关，即Nρ(E) = CutN(E,H)(因为H = V−E和NE +NV−E = N)
图的稀疏性等于分割的最小稀疏性。由此可知，(33)中稀疏度最小的切割和最小归一化切割产生相同的集合E。(NE=NH=N/2)

2.子集的边扩展,定义为(E⊂V)

其中NE≤N/2，在(33)中观察到边扩展与归一化切割的密切关系。

3.子集的Cheeger比，定义为

φ(E)的最小值称为图的Cheeger常数或传导性。这种形式与体积归一化切割密切相关。

4.2 图聚类的谱方法

这类方法是经典的有向图拓扑分析的现代替代方法，有向图拓扑分析的顶点聚类是基于图的拉普拉斯特征向量的。图聚类的实用谱方法利用了图拉普拉斯算子的几个最光滑的特征向量（λ最大时）
顶点聚类的简化算法甚至可以只使用一个特征向量，即图拉普拉斯的第二个特征向量u1，在图上产生准最优聚类或划分方案。这在一系列应用中被证明是有效的，包括图形数据处理、机器学习和计算机视觉[62]。尽管这些算法很简单，但通常是相当准确的，大量研究表明，基于第二个特征向量u1的图聚类和切割很好地逼近了最优切割[63,64]。在图的聚类和划分中使用多个平滑特征向量将增加自由度的数目，从而在数据分析的实际应用中产生更有物理意义的聚类。为了更深入的了解，在引入图谱向量及其距离的概念，以及顶点的相似度和聚类的概念之前，我们将在回顾平滑度指数。