机器学习学习笔记之——监督学习之 k-NN 算法

监督学习

mglearn 库的下载地址：
链接：https://pan.baidu.com/s/1FkRGBFgtjqsZTikLEJbtzg
提取码：4db0

监督学习是最常用也是最成功的机器学习类型之一。如果想要根据给定输入预测某个结果，并且还有输入 / 输出对的示例时，都应该使用监督学习。这些输入 / 输出对构成了机器学习模型。我们的目标是对从未见过的新数据做出准确预测。监督学习通常需要人为来构建训练集，但之后的任务本来非常费力甚至无法完成，现在却可以自动完成，通常速度很快。

1、分类与回归

监督学习问题主要有两种，分别叫做分类（classification）与回归（regression）。

• 分类问题的目标是预测类别标签（class label），这些标签来自预定义的可选列表。分类问题有时可分为二分类（binary classification）和多分类（multiclass classification）。

  在二分类中，我们通常将一个类别成为正类（positive class），另一个类别成为反类（negative class）。

• 回归任务的目标就是预测一组连续值，编程术语叫做浮点数（float-point number），数学术语叫做实数（real number）。

区分分类任务和回归任务有一个简单的方法，就是问一个问题：输出是否具有某种连续性。如果在可能的结果之间具有连续性，那么它就是一个回归问题。

---

2、泛化、过拟合和欠拟合

在监督学习中，我们想要在训练数据上构建模型，然后能够对没见过的新数据（这些新数据与训练集具有相同的特性）做出准确预测。如果一个模型能够对没见过的数据做出准确预测，我们就说它能够从训练集泛化（generalize）到测试集。我们想要构建一个泛化精度足够高的模型。

判断一个算法在新数据上表现好坏的唯一度量，就是在测试集上的评估。

• 过拟合

  如果你在拟合模型时过分关注训练集的细节，得到了一个在训练集上表现很好、但不能泛化到新数据上的模型，那么就存在过拟合。

• 欠拟合

  与之相反，如果你的模型过于简单，那么你可能无法抓住数据的全部内容以及数据中的变化，你的模型甚至在训练集上的表现就很差。

我们的模型越复杂，在训练数据上的预测结果就越好。但是，如果我们的模型过于复杂，我们开始过多关注训练集上的每一个点，模型就不能很好地泛化到新数据上。

二者之间存在一个最佳的位置，可以得到最好的泛化性能。这就是我们想要的模型。

模型复杂度与数据集大小的关系

模型复杂度与训练数据集中输入的变化密切相关：数据集中包含的数据点的变化范围越大，在不发生过拟合的前提下你可以使用的模型越复杂。通常来说，收集更多的数据点可以有更大的变化范围，所以更大的数据集可以用来构建更复杂的模型。但是，仅复制相同的数据点或收集非常相似的数据是无济于事的。

收集更多的数据，适当构建更复杂的模型，对监督学习任务往往特别有用。在现实世界中，你往往能够决定收集多少数据，这可能比模型调参更为有效。

---

3、监督学习算法

3.1、一些样本数据集

我们将使用一些数据集来说明不同的算法。其中一些数据集很小，而且是模拟的。其目的是强调算法的某个特定方面。其他数据集是现实世界的大型数据集。

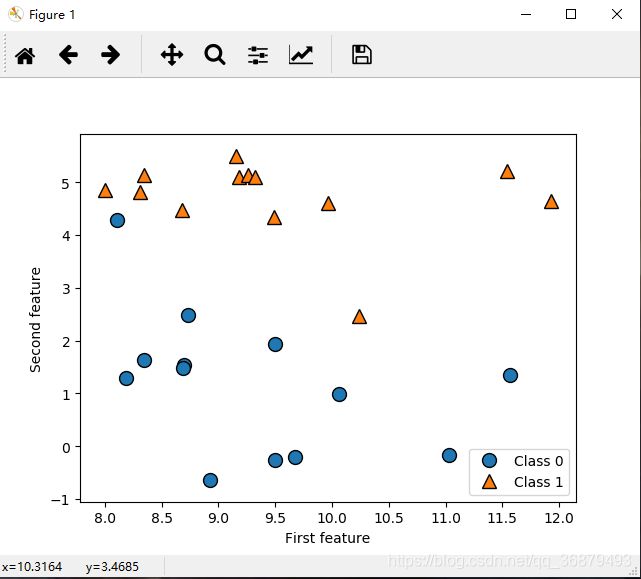
一个模拟的二分类数据集示例是 forge 数据集，它有两个特征。下列代码将绘制一个散点图，将此数据集的所有数据点可视化。图像以第一个特征为 x 轴，第二个特征为 y 轴。正如其他散点图那样，每个数据点对应图像中的一点。每个点的颜色和形状对应其类别：

# 生成数据集
X, y = mglearn.datasets.make_forge()
# 数据集绘图
mglearn.discrete_scatter(X[:, 0], X[:, 1], y)
plt.legend(["Class 0", "Class 1"], loc=4)
plt.xlabel("First feature")
plt.ylabel("Second feature")
print("X.shape: {}".format(X.shape))
# X.shape: (26, 2)

从 X.shape 可以看出，这个数据集包含 26 个数据点和 2 个特征。

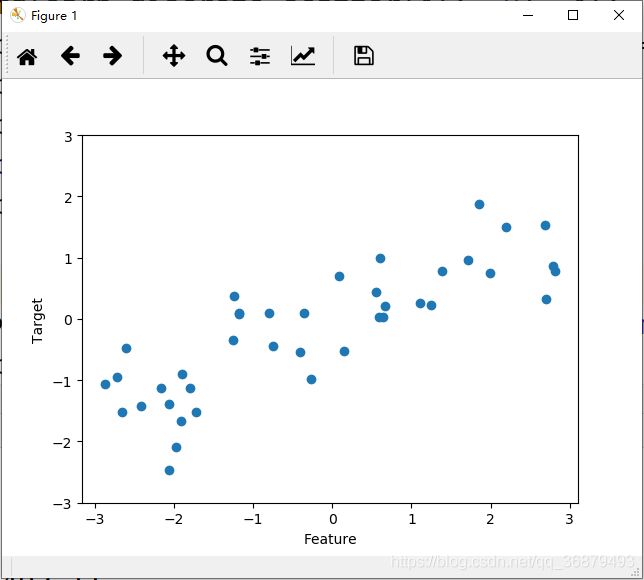
我们用模拟的 wave 数据集来说明回归算法。wave 数据集只有一个输入特征和一个连续的目标变量（或响应）。后者是模型想要预测的对象。下面绘制的图像中单一特征位于 x 轴，回归目标（输出）位于 y 轴：

X, y = mglearn.datasets.make_wave(n_samples=40)
plt.plot(X, y, 'o')
plt.ylim(-3, 3)
plt.xlabel('Feature')
plt.ylabel('Target')

我们之所以使用这些非常简单的低维数据集，是因为它们的可视化非常简单。从特征较少的数据集（也叫低维数据集）中得到的结论可能并不适用于特征较多的数据集（也叫高维数据集）。只要你记住这一点，那么在低维数据集上研究算法也是很有启发的。

除了上面这些较小的模拟的数据集，我们还将补充两个现实世界中的数据集。它们包含在 scikit-learn 中。其中的一个是威斯康星州乳腺癌数据集（简称 cancer），里面记录了乳腺癌肿瘤的临床测量数据。每个肿瘤都被标记为 “良性”或 “恶性”，其任务是基于人体组织的测量数据来学习预测肿瘤是否为恶性。

可以用 scikit-learn 模块的 load_breast_cancer 函数来加载数据：

from sklearn.datasets import load_breast_cancer
cancer = load_breast_cancer()
print("cancer.keys(): \n{}".format(cancer.keys()))
'''
cancer.keys(): 
dict_keys(['data', 'target', 'frame', 'target_names', 'DESCR', 'feature_names', 'filename'])
'''

包含在 scikit-learn 中的数据集通常被保存为 Bunch 对象，里面包含了真实数据以及一些数据集信息。关于 Bunch 对象，你只需要知道它与字典很相似，而且还有一个额外的好处，就是你可以用操作符来访问对象的值（比如用 bunch.key 来代替 bunch[‘key’]）

这个数据集共包含 569 个数据点，每个数据点有 30 个特征：

print("Shape of cancer data: {}".format(cancer.data.shape))
# Shape of cancer data: (569, 30)

在 569 个数据点中，212 个被标记为恶性，357 个被标记为良性：

print("Sample counts per class: \n {}".format(
    {n: v for n,v in zip(cancer.target_names, np.bincount(cancer.target))
     }))
# Sample counts per class: 
 {'malignant': 212, 'benign': 357}

为了得到每个特征的语义说明，我们可以看一下 feature_names 属性：

print("Feature names: \n {}".format(cancer.feature_names))
'''
Feature names: 
 ['mean radius' 'mean texture' 'mean perimeter' 'mean area'
 'mean smoothness' 'mean compactness' 'mean concavity'
 'mean concave points' 'mean symmetry' 'mean fractal dimension'
 'radius error' 'texture error' 'perimeter error' 'area error'
 'smoothness error' 'compactness error' 'concavity error'
 'concave points error' 'symmetry error' 'fractal dimension error'
 'worst radius' 'worst texture' 'worst perimeter' 'worst area'
 'worst smoothness' 'worst compactness' 'worst concavity'
 'worst concave points' 'worst symmetry' 'worst fractal dimension']
'''

可以使用 cancer.DESC 来了解数据的更多信息。

我们还会用到一个现实世界中的回归数据集，即波士顿房价数据集。与这个数据集相关的任务是，利用犯罪率、是否邻近查尔斯河、公路可达性等信息，来预测 20 世纪 70 年代波士顿地区房屋价格的中位数。这个数据集包含 506 个数据点和 13 个特征：

from sklearn.datasets import load_boston
boston = load_boston()
print("Data Shape: {}".format(boston.data.shape))	
# Data Shape: (506, 13)

对于我们的目的而言，我们需要扩展这个数据集，输入特征不仅包含这 13 个测量结果，还包括这些特征之间的乘积（也叫交互项）。换句话说，我们不仅将犯罪率和公路可达性作为特征，还将犯罪率和公路可达性的乘积作为特征。像这样包含导出特征的方法叫作特征工程（feature engineering）。这个导出的数据集可以用 load_extended_boston 函数加载。

X, y = mglearn.datasets.load_extended_boston()
print("X.shape: {}".format(X.shape))
# X.shape: (506, 104)

---

3.2、k 近邻（k-NN）

构建模型只需要保存训练数据集即可。想要对新数据点做出预测，算法会在训练数据集中找到最近的数据点，也就是它的 “最近邻”。

3.2.1、k 近邻分类

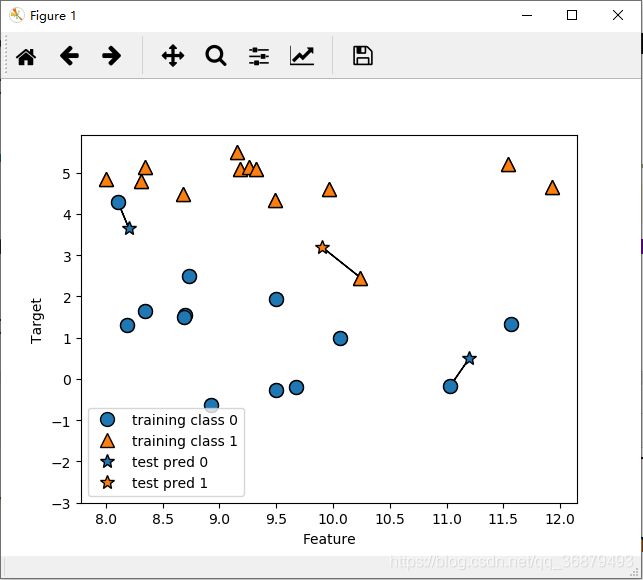
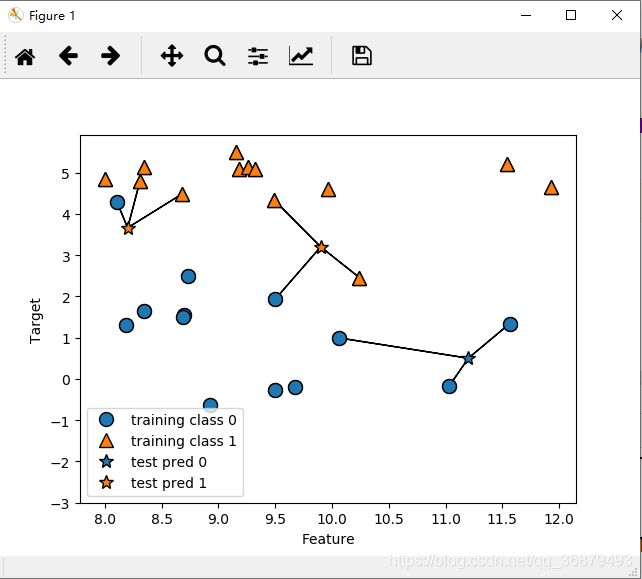
k-NN 算法最简单的版本只考虑一个最近邻，也就是与我们想要预测的数据点最近的训练数据点。预测结果就是这个训练数据点的已知输出。下图就是这种分类方法在 forge 数据集上的应用：

mglearn.plots.plot_knn_classification(n_neighbors=1)

<

这里我们添加了 3 个新数据点（用五角星表示）。对于每个新数据点，我们标记了训练集中与它最近的点。单一最近邻算法的预测结果就是那个点的标签（对应五角星的颜色）。

除了仅考虑最近邻，我还可以考虑任意个（k 个）邻居。这也是 k 近邻算法名字的由来。在考虑多于一个邻居的情况时，我们用 “投票法”（voting）来指定标签。也就是说，对于每个测试点，我们数一数多少个邻居属于类别 0，多少个邻居属于类别 1。然后将出现次数更多的类别（也就是 k 个近邻中占多数的类别）作为预测结果。下面的例子用到了 3 个近邻：

mglearn.plots.plot_knn_classification(n_neighbors=3)

可以发现，左上角新数据点的预测结果与只用一个邻居时的预测结构不同。

虽然这张图对应的是一个二分类问题，但方法同样适用于多分类的数据集。对于多分类问题，我们数一数每个类别有多少个邻居，然后将最常见的类别作为预测结果。

现在来看一下如何通过 scikit-learn 来应用 k 近邻算法。首先，将数据分为训练集和测试集，以便评估泛化性能：

from sklearn.model_selection import train_test_split
X, y = mglearn.datasets.make_forge()

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)

然后导入类并将其实例化。这时可以设定参数，比如邻居的个数。我们这里将其设为 3：

from sklearn.neighbors import KNeighborsClassifier
clf = KNeighborsClassifier(n_neighbors=3)

现在，利用训练集对这个分类器进行拟合。对于 KNeighborsClassifier 来说就是保存数据集，以便在预测时计算与邻居之间的距离：

clf.fit(X_train, y_train)

调用 predict 方法来对测试集进行预测。对于测试集中的每个数据点，都要计算它在训练集的最近邻，然后找出其中出现次数最多的类别：

print("Test set predictions : {}".format(clf.predict(X_test)))
# Test set predictions : [1 0 1 0 1 0 0]

为了评估模型的泛化能力的好坏，我们还可以对测试集和测试标签调用 score 方法：

print("Test set accuracy: {:.2f}".format(clf.score(X_test, y_test)))
# Test set accuracy: 0.86

3.2.2、分析 KNeighborsClassifier

对于二维数据集，我们还可以在 xy 平面上画出所有可能的测试点的预测结果。我们根据平面中每个点所属的类别对平面进行着色。这样可以查看决策边界（decision boundary），即算法对类别 0 和类别 1 的分界线。

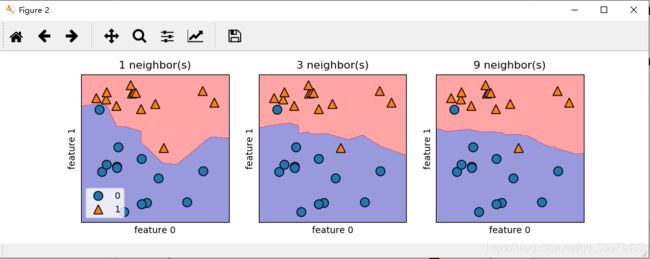
下面代码分别将 1 个、3 个和 9 个邻居的三种情况的决策边界可视化：

fig, axes = plt.subplots(1, 3, figsize=(10, 3))

for n_neighbors, ax in zip([1, 3, 9], axes):
    # fit 方法返回对象本身，所以我们可以将实例化和拟合放在一行代码中
    clf = KNeighborsClassifier(n_neighbors=n_neighbors).fit(X, y)
    mglearn.plots.plot_2d_separator(clf, X, fill=True,
                                    eps=0.5, ax=ax, alpha=.4)
    mglearn.discrete_scatter(X[:, 0], X[:, 1], y, ax=ax)
    ax.set_title("{} neighbor(s)".format(n_neighbors))
    ax.set_xlabel("feature 0")
    ax.set_ylabel("feature 1")
axes[0].legend

从左图可以看出，使用单一邻居绘制的决策边界紧跟着训练数据。随着邻居个数越来越多，决策边界也越来越平滑。更平滑的边界对应着更简单的模型。换句话说，使用更少的邻居对应着更高的模型复杂度，而使用更多的邻居对应着更低的模型复杂度。

我们来研究一下能否证实之前讨论过的模型复杂度和泛化能力之间的关系。我们将在现实世界的乳腺癌数据集上研究。先将数据集分成训练集和测试集，然后用不同的邻居个数对训练集和测试集的性能进行评估。输出如下：

X_train, X_test, y_train, y_test = train_test_split(
    cancer.data, cancer.target, stratify=cancer.target, random_state=66)

training_accuracy = []
test_accuracy = []
# n_neighbors 取值从 1 到 10
neighbors_settings = range(1, 11)

for n_neighbors in neighbors_settings:
    # 构建模型
    clf = KNeighborsClassifier(n_neighbors=n_neighbors)
    clf.fit(X_train, y_train)
    # 记录训练集精度
    training_accuracy.append(clf.score(X_train, y_train))
    # 记录泛化精度
    test_accuracy.append(clf.score(X_test, y_test))

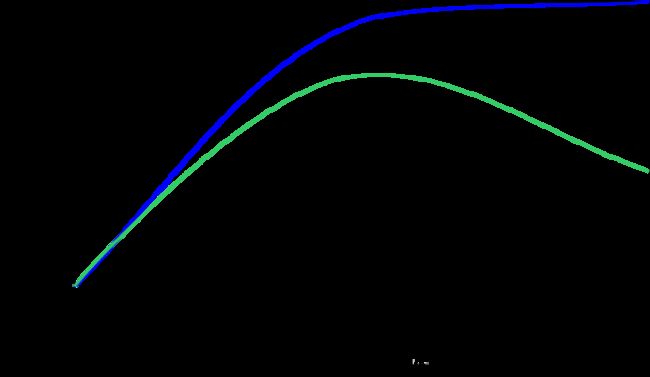
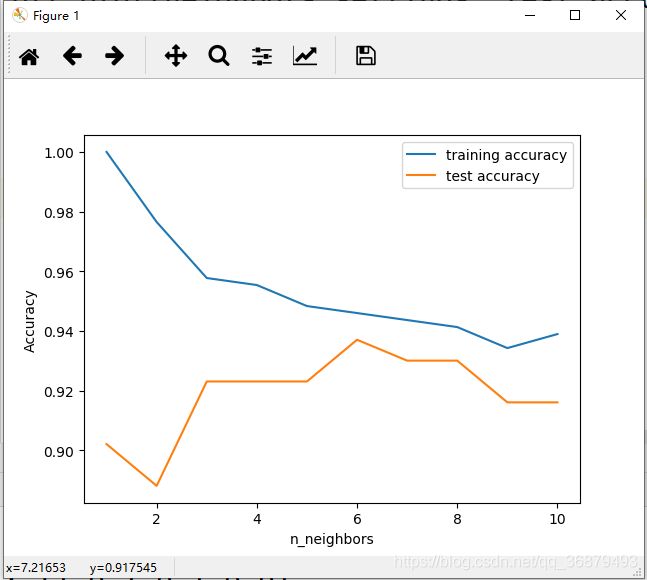
plt.plot(neighbors_settings, training_accuracy, label='training accuracy')
plt.plot(neighbors_settings, test_accuracy, label='test accuracy')
plt.ylabel('Accuracy')
plt.xlabel('n_neighbors')
plt.legend()

虽然现实世界的图像很少有非常平滑的，但我们仍可以看到过拟合和欠拟合的一些特征。仅考虑单一近邻时，训练集上的预测结果十分完美。但随着邻居个数的增加，模型变得更简单，训练集精度也随着下降。单一邻居时的测试集精度比使用更多邻居时要低，着表示单一近邻的模型过于复杂。与之相反，当考虑 10 个邻居时，模型又过于简单，性能甚至变得更差。最佳性能在中间某处。

3.2.3、k 近邻回归

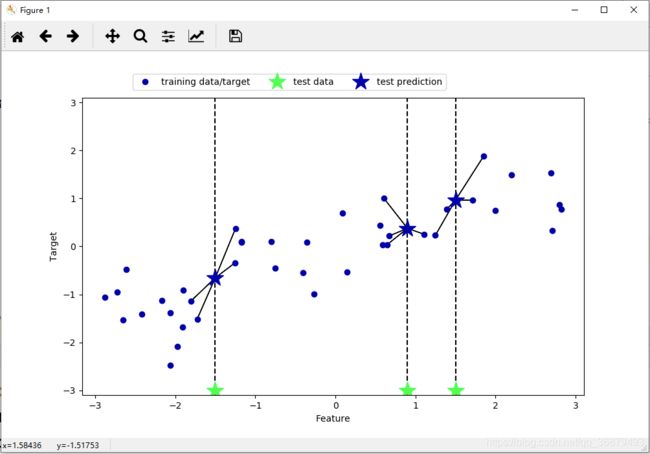
k 近邻算法还可以用于回归。我们还是先从单一近邻开始，这次使用 wave 数据集。我们添加了 3 个测试数据点，在 x 轴上用绿色五角星表示。利用单一邻居的预测结果就是最近邻的目标值。在下图中用蓝色五角星表示：

mglearn.plots.plot_knn_regression(n_neighbors=1)

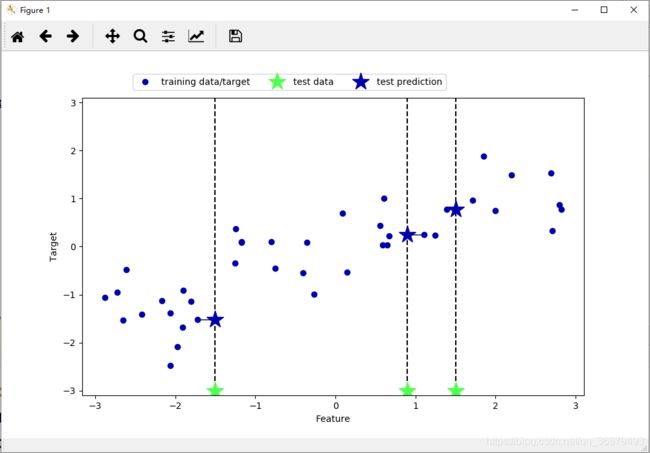
同样，也可以用多个近邻进行回归。在使用多个近邻时，预测结果为这些邻居的平均值：

mglearn.plots.plot_knn_regression(n_neighbors=4)

用于回归的 k 近邻算法在 scikit-learn 的 KNeighborsRegressor 类中实现。其用法与 KNeighborsClassifier 类似：

from sklearn.neighbors import KNeighborsRegressor
X, y = mglearn.datasets.make_wave(n_samples=40)

# 将 wave 数据集分成训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)

# 模型实例化，并将邻居个数设为 3
reg = KNeighborsRegressor(n_neighbors=3)
# 利用训练数据和训练目标来拟合模型
reg.fit(X_train, y_train)

现在可以对测试集进行预测：

print("Test set predictions: \n {}".format(reg.predict(X_test)))
'''
Test set predictions: 
 [-0.05396539  0.35686046  1.13671923 -1.89415682 -1.13881398 -1.63113382
  0.35686046  0.91241374 -0.44680446 -1.13881398]
'''

我们还可以用 score 方法来评估模型，对于回归问题，这一方法返回的是 R² 分数。R² 分数也叫作决定系数，是回归模型预测的优度度量，位于 0 到 1 之间。R² 分数等于 1 对应完美预测，R² 分数等于 0 对应常数模型，即总是预测训练集响应（y_train）的平均值：

print("Test set R^2: {:.2f}".format(reg.score(X_test, y_test)))
# Test set R^2: 0.83

3.2.4、分析 KNeighborsRegressor

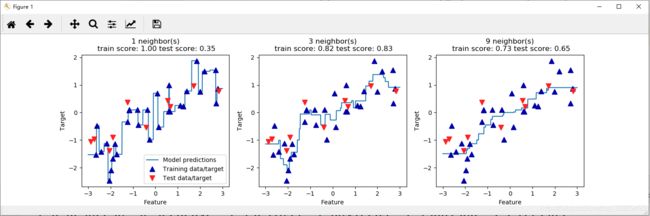
对于我们的一维数据集，可以查看所有特征取值对应的预测结果。为了便于绘图，我们创建了一个由许多点组成的测试数据集：

fig, axes = plt.subplots(1, 3, figsize=(15, 4))
# 创建 1000 个数据点，在 -3 和 3 之间均匀分布
line = np.linspace(-3, 3, 1000).reshape(-1, 1)
for n_neighbors, ax in zip([1, 3, 9], axes):
    # 利用1个、3个和 9 个邻居分别进行预测
    reg = KNeighborsRegressor(n_neighbors=n_neighbors)
    reg.fit(X_train, y_train)
    ax.plot(line, reg.predict(line))
    ax.plot(X_train, y_train, "^", c=mglearn.cm2(0), markersize=8)
    ax.plot(X_test, y_test, "v", c=mglearn.cm2(1), markersize=8)

    ax.set_title(
        "{} neighbor(s)\n train score: {:.2f} test score: {:.2f}".format(
            n_neighbors, reg.score(X_train, y_train),
            reg.score(X_test, y_test)))
    ax.set_xlabel("Feature")
    ax.set_ylabel("Target")

axes[0].legend(["Model predictions", "Training data/target",
                "Test data/target"], loc="best")

从图中可以看出，仅使用单一邻居，训练集中的每个点都对预测结果有显著影响，预测结果的图像经过所有数据点。这导致预测结果非常不稳定。考虑更多的邻居后，预测结果变得更加平滑，但对训练数据的拟合也不好。

3.2.5、优点、缺点和参数

• 参数

  1. 邻居个数

     使用较小的邻居个数（比如 3 个 或 5 个）往往能得到不错的性能

  2. 数据点之间距离的度量方法

     默认使用欧氏距离

• 优点

  1. 容易理解，在使用复杂的技术之前，尝试此算法是一种很好地基准方法
  2. 构建最近邻模型的速度很快，但如果训练集很大（特征数很多或者样本数很大），预测速度可能会很慢

• 缺点

  1. 使用 k-NN 算法时，对数据的预处理是很重要的
  2. 对于很多特征的数据集往往效果不好，对于大多数特征取值为 0 的数据集（所谓的稀疏矩阵）来说，这一算法的效果尤其不好