十大排序算法详细分析总结+图解及个人思考(上篇)-C++实现

排序概述

排序算法在学校考试，企业面试中都是高频高点，所以今天就针对这一知识点好好整理整理，也方便以后回顾复习！

排序前言

对于排序算法，不仅仅要了解算法原理，背下代码模板，更要理解该如何分析和评价一个排序算法！

所有代码均为C++，部分涉及C++11语法，均在win10平台下，VScode编译运行无误。

总览

十大排序算法分析：

排序的时间复杂度

由于排序数据的个数往往是不确定的，所以我们在分析时间复杂度时，不仅仅要考虑平均情况下的时间复杂度，还要分析在 最好情况 下的和 最坏情况 下执行效率有哪些差异，还有就是对于大部分排序算法，在执行过程中往往会涉及两个操作步骤，一个是 对元素的 比较，一个是对元素的 交换或移动，所以在分析的时候，就要改为关注 交换 或 移动 元素的次数。

排序算法的空间复杂度

一个排序算法所占用的空间的大小，不谈要排序的数据占据的空间，只谈 要实现这个排序操作需要占据的空间，这里就需要涉及一个概念：原地排序：

原地排序:就是指在排序过程中不必申请额外的存储空间，只利用原来存储待排数据的存储空间进行比较和排序的排序算法

即：原地排序不会产生多余的内存消耗

排序算法的稳定性

对于一般算法关注的主要是 时间复杂度 和 空间复杂度，对于排序算法，我们还有一个重要指标要关注，就是：排序算法的稳定性。

稳定性是指，在需要进行排序操作的数据中，如果存在值相等的元素，在排序前后，相等元素之间的排列顺序不发生改变。

我们目前学习的数据结构和算法，只是对模拟问题的思考解决，尚未完全涉及实际生活中复杂的数据，很难体会到实际中在排序中有多个数字，并且每个数字的属性会对其他属性造成的干扰，就会很本能的忽略 排序算法的稳定性。

这里引用 参考的例子(文末也会给出参考链接)，感觉很生动，瞬间理解了为什么要关注 排序算法的稳定性：Coderoger-超详细的十大排序算法总结

假如我们要给大学中的学生进行一个排序。每个学生都有两个数字属性，一个是学生所在年级，另一个是学生的年龄，最终我们希望按照学生年龄大小进行排序。而对于年龄相同的同学，我们希望按照年级从低到高的顺序排序。那么要满足这样的需求，我们应该怎么做呢？

第一个想到的，当然就是先对学生的年龄进行排序，然后再在相同年龄的区间里对年级进行排序。这种办法很直观且似乎没什么问题，但是仔细一想，会发现如果我们要进行一次完整的排序，我们需要采用5次排序算法(按年龄排序1次，四个年级分别排序4次)。那么我们有没有更好地解决办法呢？

如果我们利用具有稳定性的排序算法，这个问题就会更好地解决了。我们先按照年级对学生进行排序，然后利用稳定的排序算法，按年龄进行排序。这样，只需要运用两次排序，我们就完成了我们的目的。

基于选择的排序

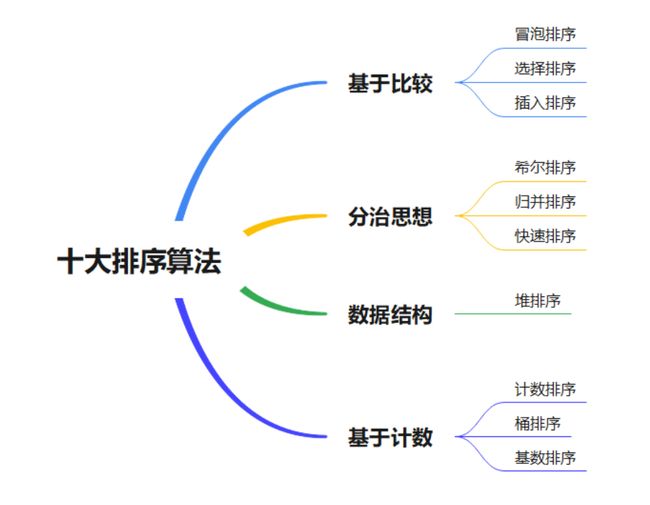
顾名思义，就是通过选择不同的数据进行交换或插入实现的排序，包括 插入排序，选择排序 和 冒泡排序。

插入排序

算法思想

首先将数组中的数据分为两个区间：一个是 已排序区间，一个是 未排序区间，这两个区间都是动态的，开始时，我们假设最左侧的元素都已经排好序了，视为 已排序区间，每一次都将 未排序区间的首个数据放入 排序号的区间内，直到未排序区间为空。

代码：

#include 
#include 

using namespace std;

void insertSort(vector<int>& arr,int len)
{
    //从1开始，认为第一个数据就是有序的第一个数据
    for(int i=1;i<len;i++)
    {
        //需要插入的元素
        int key=arr[i];
        //已排序的区间下标
        int j=i-1;
        //寻找插入位置
        while((j>=0)&&(arr[j]>key))
        {
            //元素向后移动，腾出插入位置
            arr[j+1]=arr[j];
            j--;
        }
        arr[j+1]=key;
    }
}
int main()
{
    vector<int> test={3,5,1,0,45,2,8,9,4,10,3};
    insertSort(test,test.size());
    for(auto x:test)
    {
        cout<<x<<" ";
    }
    cout<<"\n";

    system("pause");
    return 0;
}

算法分析

最好情况：数据已经有序，不用再移动任何元素，只要从头遍历一遍：$O(n)$,

最坏情况：数据为倒序，每次插入时都需要和已排序区间中所有元素进行比较，并移动元素：$O(n^2)$

平均情况：类似在数组中插入一个元素，平均时间复杂度为：$O(n^2)$

是原地排序吗？
在排序过程中，不需要额外的内存消耗，是一个原地排序算法。

是稳定排序吗？
在插入时，如果遇到相同元素，可以选择将其插入到之前元素的前面，也可以选择插入到后面，所以插入排序有可能是不稳定的。
这里我们随大流，认为 插入排序是稳定的！

选择排序

与插入排序类似，也是将数组分为 已排序 和 未排序 两个区间，但是在选择排序实现的过程中，不会发生元素的 移动，而是直接进行元素的 交换。
就可以理解为：不断在 未排序 的区间中，找到 最小的元素，放入 已排序的区间的尾部

代码：

#include 
#include 

using namespace std;

void selectionSort(vector<int>& arr)
{
    //最后一个元素必然是最大的元素，就不用再考虑了
    for(int i=0;i<arr.size()-1;i++)
    {
        int min=i;
        //确定最小元素
        for(int j=i+1;j<arr.size();j++)
        {
            if(arr[j]<arr[min])
            {
                min=j;
            }
        }
        //交换
        swap(arr[i],arr[min]);
    }
}
int main()
{
    vector<int> test={3,5,1,0,45,2,8,9,4,10,3};
    selectionSort(test);
    for(auto x:test)
    {
        cout<<x<<" ";
    }
    cout<<"\n";
    system("pause");
    return 0;
}

算法分析

最好情况和最坏情况，都要遍历 未排序区间，找到最小元素，所以时间复杂度都是 $O(n^2)$, 平均时间复杂度也都是 $O(n^2)$

是原地排序吗？
与 插入排序 一样，选择排序没有额外的内存消耗，是 原地排序

是稳定排序吗？
不是稳定排序，因为每次都要在未排序的区间中找到最小的值和前面的元素进行交换，如果遇到相同的元素，就会使他们的顺序发生交换。

冒泡排序

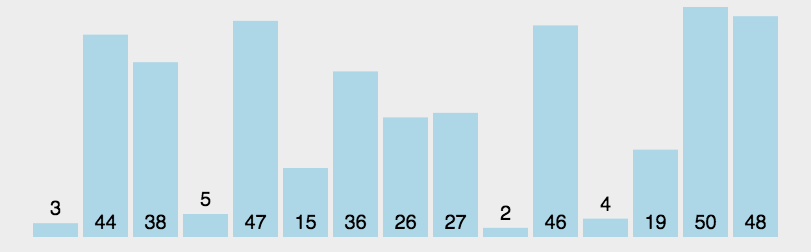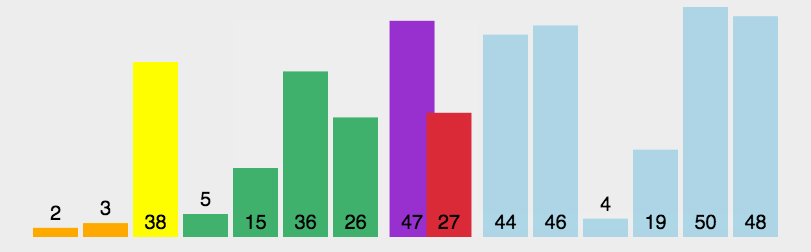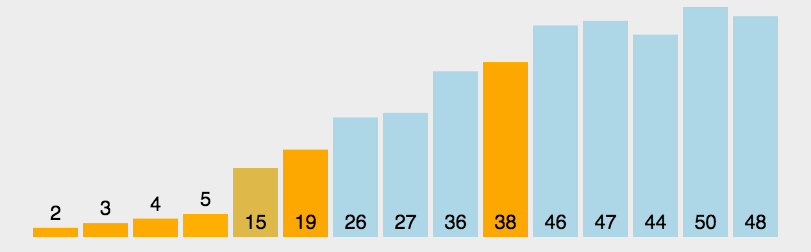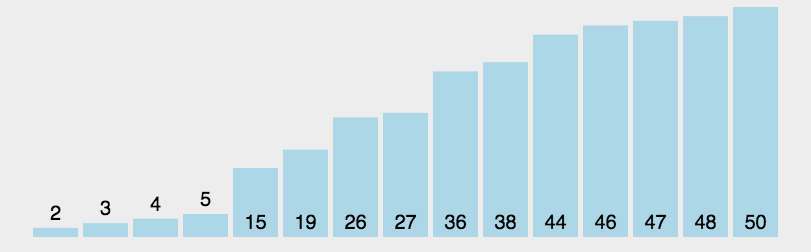
冒泡排序与插入排序不太一样，冒泡排序每次只对 相邻 两个元素进行操作，每次冒泡操作，都会 比较 相邻两个元素的大小，若不满足排序要求，就将他们交换，每一次冒泡，都会讲一个元素移动到它应该在的位置，该元素就是 未排序元素中 最大的元素

#include 
#include 

using namespace std;
void bubbleSort(vector<int>& arr)
{
    for(int i=0;i<arr.size();i++)
    {
        //注意遍历个数
        for(int j=0;j<arr.size()-i-1;j++)
        {
            //相邻元素比较，每次遇到大的就交换
            if(arr[j]>arr[j+1])
            {
                swap(arr[j],arr[j+1]);
            }
        }
    }
}
int main()
{
    vector<int> test={3,5,1,0,45,2,8,9,4,10,3};
    bubbleSort(test);
    for(auto x:test)
    {
        cout<<x<<" ";
    }
    cout<<"\n";
    system("pause");
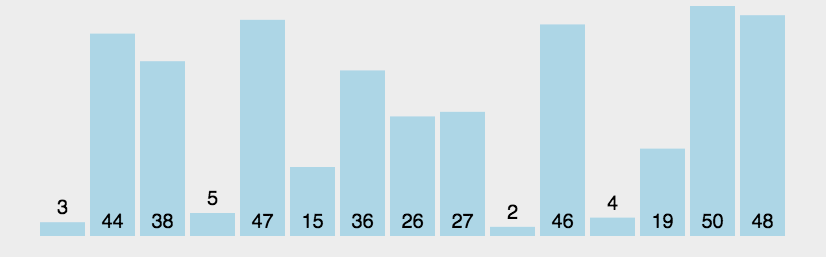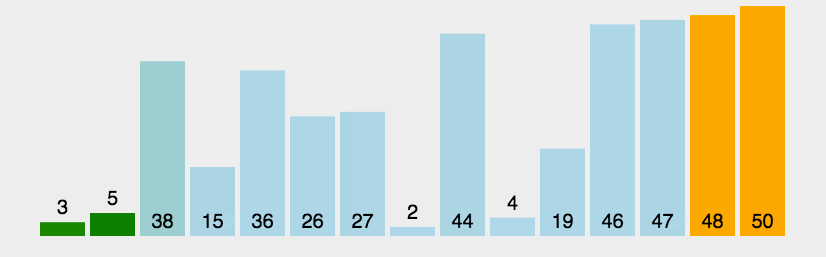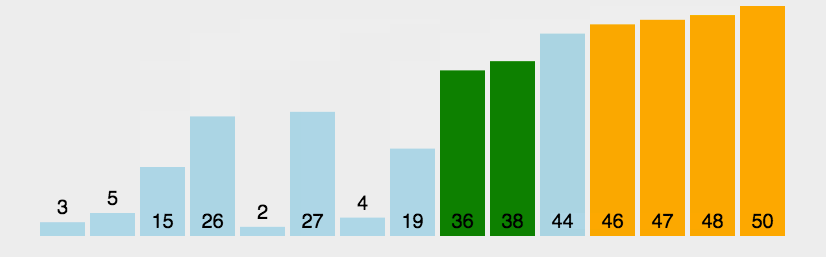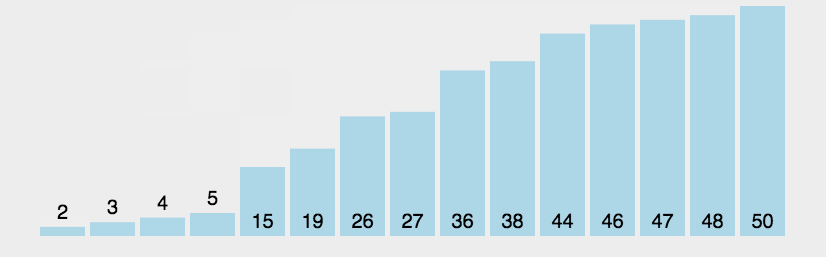
    return 0;
}

这里使用冒泡排序的思想，可以对冒泡排序，做一点优化：设置一个标志位，就可以不用每次都进行比较，进而交换，而是如果已经是有序的，就不再遍历，直接就跳出循环了

void bubble_sort(vector<int>& arr)
{
    for(int i=0;i<arr.size();i++)
    {
        //是否有序的标志位
        int flag=1;
        for(int j=0;j<arr.size()-i-1;j++)
        {
            if(arr[j]>arr[j+1])
            {
                swap(arr[j],arr[j+1]);
                //用flag为0来代表该趟排序仍然无序
                flag=0;
            }

        }
        //如果已经是有序的了，就直接跳出循环
        if(flag==1)
        {
            break;
        }
    }
}

关于冒泡排序的优化，我有篇初学C语言时整理的博客，写的还比较详细，初学者可以参考下：CSDN-夏海藻：冒泡排序及优化

算法分析

最好情况：只需要进行一次冒泡操作，没有任何元素发生交换，次数时间复杂度为：$O(n)$

最坏情况：要排序的数据 完全倒序排列，我们需要进行 $n$ 次冒泡操作，每次冒泡的时间复杂度为：$O(n)$, 所以总的时间复杂度为：$O(n^2)$

是原地排序吗？
冒泡的过程只涉及相邻数据之间的交换操作，没有额外的内存消耗，所以 冒泡排序是 原地排序算法

是稳定排序算法吗？
在冒泡的过程中，只有一次冒泡操作才会交换两个元素的顺序，所以我们为了冒泡排序的稳定性，在元素相等的情况下，我们不予交换，此时冒泡排序即为 稳定的排序

基于分治思想的排序

在计算机科学中，分治思想是很重要的算法思想，重要程度可以看做是 高中数学 的分类讨论 思想的使用。 分治法是基于 多项分支递归 的一种重要的算法思想。从名字可以看出，“分治”也就是“分而治之”的意思，就是 把一个复杂的问题分成两个或多个相同或类似的子问题，直到子问题可以简单直接地解决，原问题的解即为子问题的合并

分治算法一般都是 用 递归 来是实现的，具体的分治算法可以按照下面三个步骤来解决：

1. 分解: 将原问题分解我若干个规模较小，相对独立，与原问题形式相同的子问题
2. 解决：若子问题规模较小且容易解决，就直接解决，否则就继续递归解决各个子问题
3. 合并：将各个子问题的解合并为原问题的解

基于 分治思想的排序算法主要是 归并排序，快速排序 和 希尔排序

归并排序

归并排序的想法很简单，就是直接将数组一分为二，然后分别把左右数组排好序，再将排好序的左右两个数组合并成一个新数组，这样整个数组就全部都有序了。

1. 申请空间，使其大小为两个已排列的序列之和，该空间用来存放 合并 后的序列
2. 设定两个指针，最初的位置分别为两个 有序序列的 起始位置
3. 比较两个指针所指向的元素，选择较小的元素放入 合并孔家，并将指针移动到下一个位置
4. 重复步骤3，知道某一有序序列到达序列尾，然后将另一序列剩下的所有元素直接复制到 合并的 序列尾

#include 
#include 

using namespace std;


void merge(vector<int>& arr,int l,int r)
{
    if(l>=r)
    {
        return ;
    }
    //防止溢出
    int mid=l+r>>1;
    //生成有序序列
    merge(arr,l,mid);
    merge(arr,mid+1,r);
    
    int k=0,i=l,j=mid+1;
    vector<int> tmp(r-l+1);
    //二路归并
    while(i<=mid&&j<=r)
    {
        //先放入左边元素
        if(arr[i]<=arr[j])
        {
            tmp[k++]=arr[i++];
        }
        else
        {
            tmp[k++]=arr[j++];
        }
    }
    while(i<=mid)
    {
        tmp[k++]=arr[i++];
    }
    while(j<=r)
    {
        tmp[k++]=arr[j++];
    }

    //这里是 i=l(字母)
    for(int i=l,j=0;i<=r;i++,j++)
    {
        arr[i]=tmp[j];
    }
}

int main()
{
    vector<int> test={3,5,1,0,45,2,8,9,4,10,3};
    merge(test,0,test.size()-1);
    for(auto x:test)
    {
        cout<<x<<" ";
    }
    cout<<"\n";
    system("pause");
    return 0;
}

算法分析

归并排序的递归公式为：$T(n)=2\ast T(n/2)+n$, 即：对n个元素的递归排序需要的时间复杂度为左右子区间$n/2$ 个元素分别递归排序的时间，加上将两个已排序的子区间合并起来的时间$O(n)$, 当递归循环至最后一层时，可以推导出归并排序的(平均)时间复杂度为：$O(nlogn)$
引用证明过程如下：

是原地排序吗？
在代码中，我们需要使用一个临时数组，所以不是原地排序算法，空间复杂度为：$O(n)$

是稳定排序吗？
当我们遇到左右数组中的元素相同时，我们可以把左边的元素放入temp数组中，再放入右边数组的元素，这样就保证了相同元素的前后顺序不发生改变，所以 归并排序是一个 稳定 的排序算法。

快速排序

快排，也是利用 分治 思想实现的，具体做法是在 序列中 随机取一个元素作为哨兵元素，将所有小于该元素的放在左边，将所有大于该元素的放在右边，最后 哨兵元素的左边都是小于右边元素的(哨兵元素的右边都是大于左边的),然后 递归 的将左侧的子数组 和 右边的子数组 分别进行快速排序，这样就可以确保 整个数组都是有序的了

1. 挑选基准值：从数组中挑出一个元素，称为“基准”（pivot）
2. 分割：重新排序数组，所有比pivot小的元素摆放在pivot前面，所有比pivot值大的元素放在pivot后面(与pivot值相等的数可以到任何一边)。
3. 递归排序子数组：递归地将小于pivot元素的子序列和大于pivot元素的子序列进行快速排序。
4. 递归到最底部的判断条件是数列的大小是零或一，此时该数列显然已经有序。

#include 
#include 

using namespace std;

void quick_sort(vector<int>& arr,int l,int r)
{
    if(l>=r)
    {
        return ;
    }

    //分界
    int i=l-1,j=r+1,x=arr[l+r>>1];
    while(i<j)
    {
        do i++; while(arr[i]<x);
        do j--; while(arr[j]>x);

        if(i<j)
        {
            swap(arr[i],arr[j]);
        }
    }

    //递归左右两边
    quick_sort(arr,l,j);
    quick_sort(arr,j+1,r);

}
int main()
{
    vector<int> test={3,5,1,0,45,2,8,9,4,10,3};
    quick_sort(test,0,test.size()-1);
    for(auto x:test)
    {
        cout<<x<<" ";
    }
    cout<<"\n";
    system("pause");
    return 0;
}

算法分析

时间复杂度和上面 归并排序基本一致，如果恰好将数组分为两个大小一样的区间，则(平均)时间复杂度为：$O(nlogn)$, 在最坏情况下，时间复杂度为：$O(n^2)$

是原地排序吗？
没有额外的内存消耗，是原地排序算法

是稳定排序吗？
因为需要将 序列进行分割，并且涉及到 元素交换，顺序会发生变化，所以 快速排序 不是 一个稳定的排序。

半场总结

基于分治思想的，还有一个是 希尔排序，这个排序我们放到下半场讲解。我们先总结上半场 排序的基本特征。

上面讲的5种排序算法过程都是基于 元素之间的比较和交换，所以我们常常把这种排序算法称为 比较类排序。同时上面介绍的5种排序算法的 时间复杂度 最快也只能达到 $O(nlogn)$ (归并排序和快速排序的平均时间复杂度都是：$O(nlogn)$),所以我们也称这类排序算法称为 非线性时间比较类排序。

在下篇将介绍另外几种 线性时间非比较类排序，虽然这几种排序算法似乎效率更高，但是经过下面的介绍你就会发现，它们也并不是万能的。

最后

感谢观赏，一起提高，慢慢变强

参考

站在巨人的肩膀上

ACwing-Coderoger:超详细的十大排序算法总结

博客园-一像素:十大经典排序算法

ACwing-封禁用户：C++排序算法整理

排序面试问答 v1.0.pdf

其他内容来自网络