高斯消元法和列主销元法（Python实现）

目录

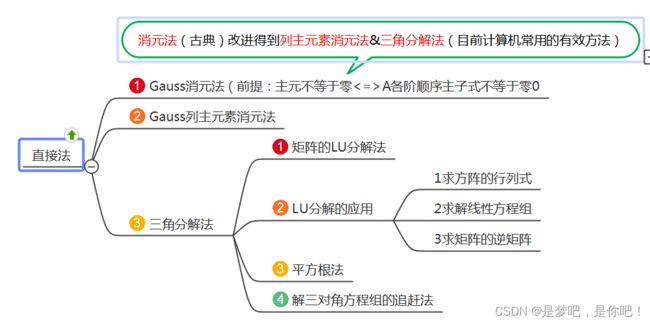
1、原理

（1）思维导图

 （2）原理

2、案例及实现 

（1）案例

（2）代码实现 

（3）结果

3、误差分析及心得体会

---

1、原理

（1）思维导图

 （2）原理

2、案例及实现 

（1）案例

（2）代码实现 

import numpy as np
# 判断系数矩阵是否为非奇异矩阵
def IsItNonSingular(A):
    row = len(A)  # 系数矩阵行数
    col = len(A[0])  # 系数矩阵列数
    # 控制第i步，A矩阵为n阶方阵
    for i in range(row - 1):
        # 若主元元素为0，则进行行变换
        if A[i][i] == 0:
            # 从后往前找出主元为0的列中，首个不为零的行
            # 对主元为0的行与此行进行行变换
            Str = []
            for h in range(row - 1, i, -1):  # 添加该列所有元素
                Str.append(A[h][i])
            Num = col - Str.index(next(filter(lambda x: x != 0, Str)))
            A[Num - 1], A[i] = A[i], A[Num - 1]  # 做行变换
        # 消元运算
        for j in range(i + 1, row, 1):
            coeff = A[j][i] / A[i][i]
            for k in range(i, col, 1):
                A[j][k] = A[j][k] - coeff * A[i][k]  # 系数矩阵消元
    # 判断该方程组系数矩阵是否为非奇异矩阵
    for i in range(row):
        if A[i][i] == 0:
            print("Coefficient matrix is not a nonsingular matrix.")
            return 'N'
    print("Coefficient matrix is a nonsingular matrix.")


def GuassElimination(A, b):
    row = len(A)  # 系数矩阵行数
    col = len(A[0])  # 系数矩阵列数
    ε = 1E-5  # 定义一个小量
    print("coefficient matrix：", A)
    print("Constant column：", b)
    # 控制第i步，高斯消元需要n-1步，A矩阵为n阶方阵
    for i in range(row - 1):
        if abs(A[i][i]) <= ε:  # 若主元为一个小量，则采用列主消元
            return None
        # 消元运算
        for j in range(i + 1, row, 1):
            coeff = A[j][i] / A[i][i]
            for k in range(i, col, 1):
                A[j][k] = A[j][k] - coeff * A[i][k]  # 系数矩阵消元
            b[j] = b[j] - coeff * b[i]  # 对应常数列消元

    # 回代过程
    x = [0] * col  # 初始化元组，用于后面存放解
    x[col - 1] = b[col - 1] / A[col - 1][col - 1]  # 第n个解
    for i in range(row - 2, -1, -1):
        for j in range(col - 1, i, -1):
            b[i] = b[i] - A[i][j] * x[j]
        x[i] = b[i] / A[i][i]
    print("The solution of the equations is：")
    for i in range(col):
        print("x{}:".format(i + 1), '%.8f' % x[i])
    print("\n")
    return x


def ColumnPrincipalElimination(A, b):
    row = len(A)  # 系数矩阵行数
    col = len(A[0])  # 系数矩阵列数
    print("coefficient matrix：", A)
    print("Constant column：", b)
    # 控制第i步，消元需要n-1步，A矩阵为n阶方阵
    for i in range(row - 1):
        # 每步运算前找出列中绝对值最大元素
        # 作行变换，让绝对值最大的元素行作主元
        Str = []
        for j in range(i, row, 1):
            Str.append(A[j][i])
        Num = Str.index(max(Str)) + i
        A[Num], A[i] = A[i], A[Num]  # 行变换
        b[Num], b[i] = b[i], b[Num]

        # 消元运算
        for j in range(i + 1, row, 1):
            coeff = A[j][i] / A[i][i]
            for k in range(i, col, 1):
                A[j][k] = A[j][k] - coeff * A[i][k]  # 系数矩阵消元
            b[j] = b[j] - coeff * b[i]  # 对应常数列消元

    # 回代过程
    x = [0] * col  # 初始化元组，用于后面存放解
    x[col - 1] = b[col - 1] / A[col - 1][col - 1]  # 第n个解
    for i in range(row - 2, -1, -1):
        for j in range(col - 1, i, -1):
            b[i] = b[i] - A[i][j] * x[j]
        x[i] = b[i] / A[i][i]
    print("The solution of the equations is：")
    for i in range(col):
        print("x{}:".format(i + 1), '%.8f' % x[i])
    # print("\n")
    return x
def main():
    b1 = [0.4043, 0.1550, 0.4240, -0.2557]
    b2 = [0.4043, 0.1550, 0.4240, -0.2557]
    test1 = [[0.4096, 0.1234, 0.3678, 0.2943], [0.2246, 0.3872, 0.4015, 0.1129], [0.3645, 0.1920, 0.3781, 0.0643],
                  [0.1784, 0.4002, 0.2785, 0.3927]]
    test2 = [[0.4096, 0.1234, 0.3678, 0.2943], [0.2246, 0.3872, 0.4015, 0.1129], [0.3645, 0.1920, 0.3781, 0.0643],
                  [0.1784, 0.4002, 0.2785, 0.3927]]
    # python为动态语言，
    # 在判断非奇异矩阵过程中会改动初值
    # 故重新赋值
    IsItNonSingular(test1)
    print("test1 Gaussian elimination test：")
    test1 = [[0.4096, 0.1234, 0.3678, 0.2943], [0.2246, 0.3872, 0.4015, 0.1129], [0.3645, 0.1920, 0.3781, 0.0643],
                  [0.1784, 0.4002, 0.2785, 0.3927]]
    GuassElimination(test1, b1)

    IsItNonSingular(test2)
    print("test2Gaussian column principal elimination test：")
    test2 = [[0.4096, 0.1234, 0.3678, 0.2943], [0.2246, 0.3872, 0.4015, 0.1129], [0.3645, 0.1920, 0.3781, 0.0643],
                  [0.1784, 0.4002, 0.2785, 0.3927]]
    ColumnPrincipalElimination(test2, b2)


if __name__ == '__main__':
    main()

（3）结果

Coefficient matrix is a nonsingular matrix.
test1 Gaussian elimination test：
coefficient matrix： [[0.4096, 0.1234, 0.3678, 0.2943], [0.2246, 0.3872, 0.4015, 0.1129], [0.3645, 0.192, 0.3781, 0.0643], [0.1784, 0.4002, 0.2785, 0.3927]]
Constant column： [0.4043, 0.155, 0.424, -0.2557]
The solution of the equations is：
x1: -0.18034012
x2: -1.66163443
x3: 2.21499710
x4: -0.44669701


Coefficient matrix is a nonsingular matrix.
test2Gaussian column principal elimination test：
coefficient matrix： [[0.4096, 0.1234, 0.3678, 0.2943], [0.2246, 0.3872, 0.4015, 0.1129], [0.3645, 0.192, 0.3781, 0.0643], [0.1784, 0.4002, 0.2785, 0.3927]]
Constant column： [0.4043, 0.155, 0.424, -0.2557]
The solution of the equations is：
x1: -0.18034012
x2: -1.66163443
x3: 2.21499710
x4: -0.44669701

Process finished with exit code 0

3、误差分析及心得体会