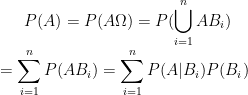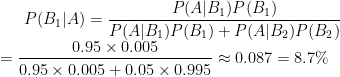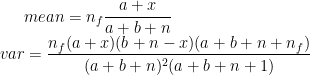hardworking mole
hardworking mole

贝叶斯数据分析

1.基础知识

条件概率公式：

对于任意两个事件A和B，且P(A)>0,定义在A发生的条件下，B发生的条件概率为

P(B|A)=\frac{P(AB)}{P(A)}

从而P(AB)=P(A)P(B|A),这就是乘法公式

推而广之，设A_1,A_2,...,A_n是任意n个随机事件，则有更一般的乘法公式

P(A_1A_2...A_n)=P(A_1)P(A_2|A_1)P(A_3|A_1A_2)...P(A_n|A_1A_2...A_{n-1})

全概率公式：

设B_1,...B_n是样本空间\Omega中的一个完备事件群（又称为\Omega的一个划分）。换言之，它们满足下列条件：

(a)两两不相交，即B_i\bigcap B_j=\varnothing (i\neq j)

(b)它们的并（和）恰好是样本空间，即\bigcup_{i=1}^{n}B_i=\Omega

设A为\Omega中的一个事件，则全概率公式为

P(A)=P(A\Omega )=P(\bigcup_{i=1}^{n}AB_i)\\ =\sum_{i=1}^{n}P(AB_i)=\sum_{i=1}^{n}P(A|B_i)P(B_i)

这个公式将事件A分解成一些两两不相交的事件之并。直接计算P(A)不容易，但分解后的那些事件的概率容易计算，从而使P(A)的计算变得容易了。

2.贝叶斯公式

在全概率公式的条件下，即存在样本空间\Omega的一个完备事件群\left \{ B_1,...B_n \right \},设A为\Omega中的一个事件，且P(B_i)>0(i=1,...,n),P(A)>0,则按照条件概率的计算方法，有

P(B_i|A)=\frac{P(A|B_i)P(B_i)}{P(A)}=\frac{P(A|B_i)P(B_i)}{\sum_{j=1}^{n}P(A|B_j)P(B_j)}

示例：一种诊断某癌症的试剂，经临床实验有如下记录：癌症病人试验结果是阳性的概率为95%，非癌症病人试验结果是阴性的概率为95%。现用这种试剂在某社区进行癌症筛查，该社区癌症发病率为0.5%,问某人反应为阳性时，该如何判断他是否患有癌症？

解：设事件A表示“试验结果是阳性”，事件B表示“被诊断者患癌症”，则B_1=B和B_2=\bar{B}构成一个完备事件群。由题意知：

P(A|B_1)=0.95,P(A|B_2)=0.05,P(B_1)=0.005,P(B_2)=0.995

现需计算P(B_1|A),P(B_2|A).由贝叶斯公式得

P(B_1|A)=\frac{P(A|B_1)P(B_1)}{P(A|B_1)P(B_1)+P(A|B_2)P(B_2)}\\ =\frac{0.95\times0.005}{0.95\times0.005+0.05\times0.995}\approx 0.087=8.7%

P(B_2|A)=1-P(B_1|A)=91.3%

练习：用贝叶斯公式解释“幸存者偏差”现象

用X表示飞机被击中的部位，取值集合为{机头，机翼，机身，机尾}

Y=0表示飞机坠毁

我们关心的是那些坠毁飞机被击中部位的分布

P(X|Y=0)=\frac{P(Y=0|X)P(X)}{P(Y=0)}\propto P(Y=0|X)P(X)

即关心X为哪些部位时，P(X|Y=0)比较大，从而应该加强这些部位的防护。由于二战期间的炮弹是不长眼睛的，所以可以将P(X)视为均匀分布，从而得到

P(X|Y=0)\propto P(Y=0|X)P(X)\propto P(Y=0|X)

类似地，可以得到

P(X|Y=1)\propto P(Y=1|X)P(X)\propto P(Y=1|X)

同时注意到P(Y=0|X)+P(Y=1|X)=1

我们仅能观察到返航飞机上弹痕的分布P(X|Y=1)，所以当某一部位X（例如机身）的弹痕较多时，说明P(X=机身|Y=1)较大，根据上述关系得到P(Y=1|X=机身)较大，而P(Y=0|X=机身)和P(X=机身|Y=0）较小，从而说明机身不是关键部位；相反地，如果另一部位X（例如机翼）弹痕较少时，该部位往往可能是关键部位，应加强防护。

贝叶斯公式也可用于纠正一些“成功学谬误”

3.贝叶斯统计学与经典统计学的主要区别

基于总体信息、样本信息、先验信息进行统计推断的方法和理论称为贝叶斯统计学。

  • 贝叶斯统计学与经典统计学的主要区别在于是否利用先验信息。
  • 在使用样本上存在差别，贝叶斯方法重视已出现的样本，对尚未发生的样本值不予考虑。
  • 贝叶斯学派重视先验信息的收集、挖掘和加工，使之形成先验分布而参加到统计推断中来，以提高统计推断的效果。

古典学派与贝叶斯学派的主要分歧：

（1）对于概率含义的解释：

        古典学派：一个事件的概率可以用大量重复试验下的频率来解释

        贝叶斯学派：将主观概率认为是认识主体对事件发生机会的相信程度，因为有些事件不可重复

（2）对于参数的理解：

        古典学派：参数是一个固定值，虽然可能未知，但可以推断

        贝叶斯学派：参数是随机变量，具有特定分布

4.贝叶斯参数估计

贝叶斯参数估计是基于贝叶斯公式的参数估计方法

p(\theta|x)=\frac{p(x|\theta) p(\theta)}{p(x)}=\frac{p(x|\theta )p(\theta )}{\int p(x|\theta )p(\theta )d\theta }

        其中，p(\theta |x)是参数\theta的后验分布，p(x|\theta )是x关于\theta的似然函数，p(\theta )是参数\theta的先验分布，p(x)是x的边缘分布，亦称归一化因子

 4.1先验分布是均匀分布的掷硬币试验

示例：掷硬币试验，掷出n次，设随机变量X表示正面向上的次数，因此随机变量X服从二项分布Bin(n,\theta),\theta是硬币正面向上的概率，概率分布如下：

p(X=x|\theta )=C_n^x \theta^x(1-\theta)^{n-x},x=0,1,...,n,

        其中x表示观测到正面向上的次数。

x关于参数\theta的似然函数p(X|\theta )=C_n^x \theta^x(1-\theta)^{n-x},x=0,1,...,n,(将掷出n次硬币看做一次掷n枚，x枚朝上)

参数\theta的先验分布：选取[0,1]区间上的均匀分布

p(\theta )=1,0\leq \theta \leq 1

x的边缘分布（归一化因子）

p(x)=\int_{0}^{1}p(x|\theta )p(\theta )d\theta =\int_{0}^{1}\binom{n}{x}\theta ^x(1-\theta )^{n-x}d\theta =\frac{1}{1+n}

将上述三项代入贝叶斯公式，得到参数\theta的后验分布

p(\theta |x)=(1+n)\binom{n}{x}\theta ^x(1-\theta )^{n-x}

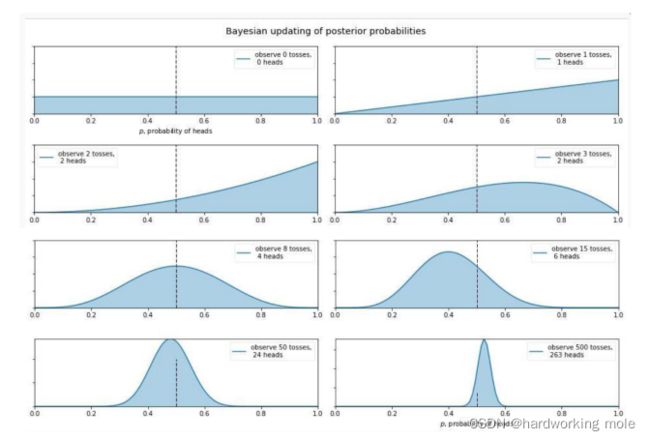
事实上，掷硬币试验的先验分布不一定为均匀分布。我们不妨将试验的先验分布设定为Beta分布，再次代入贝叶斯公式，来观察后验分布会有何变化。

4.2先验分布为Beta分布的掷硬币试验

首先对Beta分布进行简要介绍。

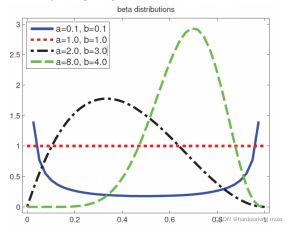
Beta分布是一组定义在[0,1]区间上的连续概率分布

Beta分布的概率密度函数为

Beta(\theta |a,b)=\left\{\begin{matrix} \frac{1}{B(a,b)}\theta ^{a-1}(1-\theta )^{b-1},0\leq \theta \leq 1\\ 0,others \end{matrix}\right.

        其中B(a,b)是Beta函数，定义为

B(a,b)=\frac{\Gamma (a)\Gamma (b)}{\Gamma (a+b)}

        其中\Gamma(\cdot )是Gamma函数，定义为

\Gamma (s)=\int_{0}^{\infty }x^{s-1}e^{-x}dx,s>0

参数a和b控制着Beta分布的形式

贝叶斯数据分析_第1张图片

  • 特别地，当a=b=1时，Beta分布就是[0,1]区间上的均匀分布
  • Beta分布通常作为二项分布的参数的先验分布使用

Beta分布的期望、众数、方差

mean=\frac{a}{a+b},mode=\frac{a-1}{a+b-2},var=\frac{ab}{(a+b)^2(a+b+1)}

回到掷硬币试验

将参数\theta的先验分布设定为Beta分布

Beta(\theta |a,b)=\frac{1}{B(a,b)}\theta ^{a-1}(1-\theta )^{b-1}

当a=b=1时，Beta分布就是[0,1]区间上的均匀分布

x的边缘分布（归一化因子）可以写为

p(x)=\int_{0}^{1}p(x|\theta )p(\theta )d\theta \\ =\int_{0}^{1}\binom{n}{x}\theta ^x(1-\theta )^{n-x}\frac{\Gamma (a+b)}{\Gamma (a)\Gamma (b)}\theta ^{a-1}(1-\theta )^{b-1}d\theta\\ =\binom{n}{x}\frac{\Gamma (a+b)}{\Gamma (a)\Gamma (b)}\int_{0}^{1}\theta ^{a+x-1}(1-\theta )^{b+n-x-1}d\theta \\ =\binom{n}{x}\frac{\Gamma (a+b)}{\Gamma (a)\Gamma (b)}\frac{\Gamma (a+x)\Gamma (b+n-x)}{\Gamma (a+b+n)}\int_{0}^{1}\frac{\Gamma (a+b+n)}{\Gamma (a+x)\Gamma (b+n-x)}\theta ^{a+x-1}(1-\theta )^{b+n-x-1}d\theta \\ =\binom{n}{x}\frac{\Gamma (a+b)}{\Gamma (a)\Gamma (b)}\frac{\Gamma (a+x)\Gamma (b+n-x)}{\Gamma (a+b+n)}\\ =\binom{n}{x}\frac{B(a+x,b+n-x)}{B(a,b)}

将x的边缘分布p(x)代入贝叶斯公式

p(\theta |x)=\frac{p(x|\theta )p(\theta )}{p(x)}\\ =\frac{\binom{n}{x}\theta ^x(1-\theta )^{n-x}\frac{1}{B(a,b)}\theta ^{a-1}(1-\theta )^{b-1}}{\binom{n}{x}\frac{B(a+x,b+n-x)}{B(a,b)} }\\ =Beta(\theta |a+x,b+n-x)

\theta的后验分布是参数为a+x和b+n-x的Beta分布。进一步可以发现，事实上a+x代表的即是硬币先验及后验中向上的总次数；b+n-x代表的是硬币先验及后验中向下的总次数。

后验概率密度最大的点（众数mode）是

\hat{\theta}_{MAP}=\frac{a+x-1}{a+b+n-2}

        称之为极大后验估计

考虑到极大似然估计(MLE)的结果为\hat{\theta }_{MLE}=\frac{x}{n},因此，后验众数可以看成极大似然估计结果和先验众数的加权组合。

\frac{a+x-1}{a+b+n-2}=w\times\frac{x}{n}+(1-w)\times\frac{a-1}{a+b-2}

        其中，w=\frac{n}{a+b+n-2}

当n变大，w趋向于1，后验众数趋向于极大似然估计结果

当a=b=1时，w=1，后验众数等于极大似然估计结果，极大后验估计结果与极大似然估计结果相同。

同理，若取后验均值作为贝叶斯参数估计的结果，\hat{\theta }_{Mean}=\frac{a+x}{a+b+n}

  • \hat{\theta }_{Mean}在小样本情形下比\hat{\theta }_{MLE}更合理
  • 当试验次数n增加时，\hat{\theta }_{Mean}趋向于\hat{\theta }_{MLE}
  • 使用先验原因：因为有些试验不能大量重复进行

贝叶斯数据分析_第2张图片

贝叶斯原理符合人们认知事物的模式：先验+数据=后验

 4.3后验预测分布

在已经掷出n次硬币并观测到x次正面向上的试验结果上，预测重新掷出n_f次硬币正面向上的次数y

后验预测分布:

首先，利用p(y,\theta)=p(y|\theta)p(\theta),第一次掷硬币与第二次结果无关两个条件，

p(y,\theta|n_f,x,n)=p(y|\theta,n_f,x,n)p(\theta|n_f,x,n)=p(y|n_f,\theta)p(\theta|x,n)

那么，后验预测分布为

p(y|n_f,x,n)=\int p(y,\theta|n_f,x,n)d\theta\\ =\int p(y|n_f,x,n,\theta)p(\theta|x,n)d\theta\\ =\int p(y|n_f,\theta)p(\theta|x,n)d\theta\\ =\int Bin(y|n_f,\theta)Beta(\theta|a+x,b+n-x)d\theta\\ =\int C_{n_f}^y\theta^y(1-\theta)^{n_f-y}\frac{\theta^{a+x-1}(1-\theta)^{b+n-x-1}}{B(a+x,b+n-x)}d\theta\\ =\frac{C^y_{n_f}}{B(a+x,b+n-x)}\int \theta ^{a+x+y-1}(1-\theta)^{b+n-x+n_f-y-1}d\theta\\ =C_{n_f}^y\frac{B(a+x+y,b+n-x+n_f-y)}{B(a+x,b+n-x)}

期望和方差分别为：

mean=n_f\frac{a+x}{a+b+n}\\ var=\frac{n_f(a+x)(b+n-x)(a+b+n+n_f)}{(a+b+n)^2(a+b+n+1)}

5.共轭先验

在硬币实验中，参数\theta的先验分布p(\theta)和后验分布p(\theta|x)都是Beta分布，称Beta分布是二项分布的共轭先验分布。

当先验分布和后验分布是同一种分布，称先验分布是似然函数的共轭先验分布。

只有给定似然函数，才能确定其共轭先验分布。也就是说，必须根据问题的性质选取其共轭先验分布。常见的共轭先验分布如下：

似然函数 参数 共轭先验分布
二项分布 成功概率 贝塔分布（Beta）
多项分布 成功概率 狄利克雷分布（Dirichlet）
泊松分布 参数\lambda 伽马分布（Gamma）
指数分布 参数\lambda 伽马分布（Gamma）
正态分布-方差已知 均值 正态分布（Normal,Gaussian）
正态分布-均值已知 方差 逆伽马分布（Inverse Gamma）

 对于一般形式的似然函数，共轭先验分布可能不存在

若选取某种分布作为参数\theta的先验分布，x的边缘分布（归一化因子）很可能没有解析表达式

p(x)=\int_{0}^{1}p(x|\theta)p(\theta)d\theta

这将导致参数\theta的后验分布没有解析表达式。解决方法：（1）Markov Chain Monte Carlo(MCMC)(2）Variational Inference(VI)

6.贝叶斯方法的应用

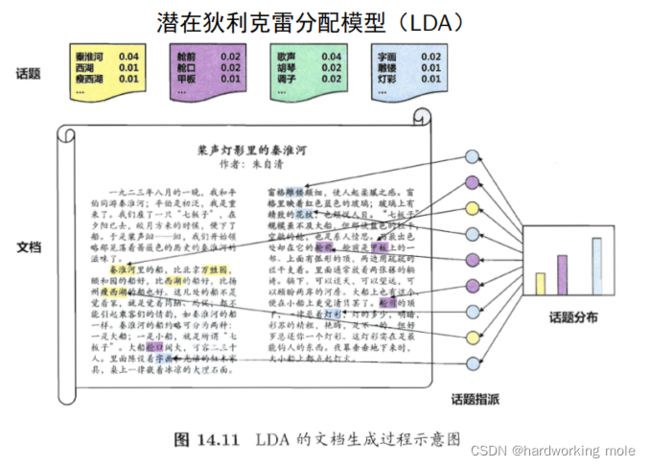
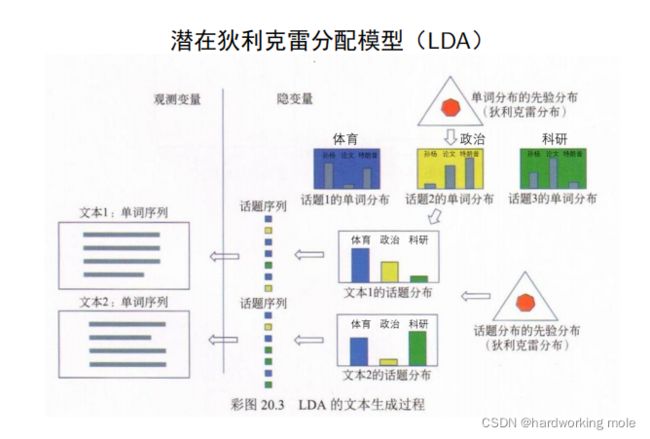
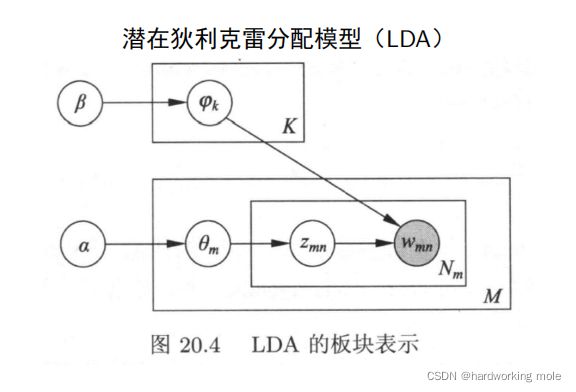
潜在狄利克雷的分配模型（LDA）

贝叶斯数据分析_第3张图片

贝叶斯数据分析_第4张图片 

贝叶斯数据分析_第5张图片

 

 

你可能感兴趣的:(概率论,nlp,自然语言处理)

  • 探索OpenAI和LangChain的适配器集成：轻松切换模型提供商 nseejrukjhad langchaineasyui前端python
    #探索OpenAI和LangChain的适配器集成：轻松切换模型提供商##引言在人工智能和自然语言处理的世界中，OpenAI的模型提供了强大的能力。然而，随着技术的发展，许多人开始探索其他模型以满足特定需求。LangChain作为一个强大的工具，集成了多种模型提供商，通过提供适配器，简化了不同模型之间的转换。本篇文章将介绍如何使用LangChain的适配器与OpenAI集成，以便轻松切换模型提供商
  • 使用Apify加载Twitter消息以进行微调的完整指南 nseejrukjhad twittereasyui前端python
    #使用Apify加载Twitter消息以进行微调的完整指南##引言在自然语言处理领域，微调模型以适应特定任务是提升模型性能的常见方法。本文将介绍如何使用Apify从Twitter导出聊天信息，以便进一步进行微调。##主要内容###使用Apify导出推文首先，我们需要从Twitter导出推文。Apify可以帮助我们做到这一点。通过Apify的强大功能，我们可以批量抓取和导出数据，适用于各类应用场景。
  • 深入理解 MultiQueryRetriever：提升向量数据库检索效果的强大工具 nseejrukjhad 数据库python
    深入理解MultiQueryRetriever：提升向量数据库检索效果的强大工具引言在人工智能和自然语言处理领域，高效准确的信息检索一直是一个关键挑战。传统的基于距离的向量数据库检索方法虽然广泛应用，但仍存在一些局限性。本文将介绍一种创新的解决方案：MultiQueryRetriever，它通过自动生成多个查询视角来增强检索效果，提高结果的相关性和多样性。MultiQueryRetriever的工
  • 自然语言处理_tf-idf _feivirus_ 算法机器学习和数学自然语言处理tf-idf逆文档频率词频
    importpandasaspdimportmath1.数据预处理docA="Thecatsatonmyface"docB="Thedogsatonmybed"wordsA=docA.split("")wordsB=docB.split("")wordsSet=set(wordsA).union(set(wordsB))print(wordsSet){'on','my','face','sat',
  • 免费的GPT可在线直接使用（一键收藏） kkai人工智能 gpt
    1、LuminAI（https://kk.zlrxjh.top）LuminAI标志着一款融合了星辰大数据模型与文脉深度模型的先进知识增强型语言处理系统，旨在自然语言处理（NLP）的技术开发领域发光发热。此系统展现了卓越的语义把握与内容生成能力，轻松驾驭多样化的自然语言处理任务。VisionAI在NLP界的应用领域广泛，能够胜任从机器翻译、文本概要撰写、情绪分析到问答等众多任务。通过对大量文本数据的
  • 推荐3家毕业AI论文可五分钟一键生成！文末附免费教程！ 小猪包333 写论文人工智能AI写作深度学习计算机视觉
    在当前的学术研究和写作领域，AI论文生成器已经成为许多研究人员和学生的重要工具。这些工具不仅能够帮助用户快速生成高质量的论文内容，还能进行内容优化、查重和排版等操作。以下是三款值得推荐的AI论文生成器：千笔-AIPassPaper、懒人论文以及AIPaperPass。千笔-AIPassPaper千笔-AIPassPaper是一款基于深度学习和自然语言处理技术的AI写作助手，旨在帮助用户快速生成高质
  • AI论文题目生成器怎么用？9款论文写作网站简单3步搞定 小猪包333 写论文人工智能深度学习计算机视觉
    在当今信息爆炸的时代，AI写作工具的出现极大地提高了写作效率和质量。本文将详细介绍9款优秀的论文写作网站，并重点推荐千笔-AIPassPaper。一、千笔-AIPassPaper千笔-AIPassPaper是一款功能强大的AI论文生成器，基于最新的自然语言处理技术，能够一键生成高质量的毕业论文、开题报告等文本内容。它不仅提供智能选题、文献推荐和论文润色等功能，还具有较高的用户评价。其文献综述生成功
  • AI大模型的架构演进与最新发展 季风泯灭的季节 AI大模型应用技术二人工智能架构
    随着深度学习的发展，AI大模型（LargeLanguageModels,LLMs）在自然语言处理、计算机视觉等领域取得了革命性的进展。本文将详细探讨AI大模型的架构演进，包括从Transformer的提出到GPT、BERT、T5等模型的历史演变，并探讨这些模型的技术细节及其在现代人工智能中的核心作用。一、基础模型介绍：Transformer的核心原理Transformer架构的背景在Transfo
  • 机器学习-聚类算法 不良人龍木木 机器学习机器学习算法聚类
    机器学习-聚类算法1.AHC2.K-means3.SC4.MCL仅个人笔记，感谢点赞关注！1.AHC2.K-means3.SC传统谱聚类：个人对谱聚类算法的理解以及改进4.MCL目前仅专注于NLP的技术学习和分享感谢大家的关注与支持！
  • 轻量级模型解读——轻量transformer系列 lishanlu136 #图像分类轻量级模型transformer图像分类
    先占坑，持续更新。。。文章目录1、DeiT2、ConViT3、Mobile-Former4、MobileViTTransformer是2017谷歌提出的一篇论文，最早应用于NLP领域的机器翻译工作，Transformer解读，但随着2020年DETR和ViT的出现(DETR解读，ViT解读)，其在视觉领域的应用也如雨后春笋般渐渐出现，其特有的全局注意力机制给图像识别领域带来了重要参考。但是tran
  • FlagEmbedding 吉小雨 python库python
    FlagEmbedding教程FlagEmbedding是一个用于生成文本嵌入（textembeddings）的库，适合处理自然语言处理（NLP）中的各种任务。嵌入（embeddings）是将文本表示为连续向量，能够捕捉语义上的相似性，常用于文本分类、聚类、信息检索等场景。官方文档链接：FlagEmbedding官方GitHub一、FlagEmbedding库概述1.1什么是FlagEmbeddi
  • 【NumPy】深入解析numpy.zeros()函数 二七830 numpy
    欢迎莅临我的个人主页这里是我深耕Python编程、机器学习和自然语言处理（NLP）领域，并乐于分享知识与经验的小天地！博主简介：我是二七830，一名对技术充满热情的探索者。多年的Python编程和机器学习实践，使我深入理解了这些技术的核心原理，并能够在实际项目中灵活应用。尤其是在NLP领域，我积累了丰富的经验，能够处理各种复杂的自然语言任务。技术专长：我熟练掌握Python编程语言，并深入研究了机
  • Humanize 项目教程 尤嫒冰
    Humanize项目教程humanizeAJSlibraryforaddinga“humantouch”todata.项目地址:https://gitcode.com/gh_mirrors/humani/humanize项目介绍Humanize是一个开源项目，旨在将机器生成的文本转换为更加自然、人性化的文本。该项目通过先进的算法和自然语言处理技术，使得AI生成的内容更加贴近人类的表达方式，从而提高
  • 全自动解密解码神器 — Ciphey K'illCode python_模块pythonvscode
    Ciphey是一个使用自然语言处理和人工智能的全自动解密/解码/破解工具。简单地来讲，你只需要输入加密文本，它就能给你返回解密文本。就是这么牛逼。有了Ciphey，你根本不需要知道你的密文是哪种类型的加密，你只知道它是加密的，那么Ciphey就能在3秒甚至更短的时间内给你解密，返回你想要的大部分密文的答案。下面就给大家介绍Ciphey的实战使用教程。1.准备开始之前，你要确保Python和pip已
  • CV、NLP、数据控掘推荐、量化 海的那边- AI算法自然语言处理人工智能
    下面是对CV（计算机视觉）、NLP（自然语言处理）、数据挖掘推荐和量化的简要概述及其应用领域的介绍：1.CV（计算机视觉，ComputerVision）定义：计算机视觉是一门让计算机能够从图像或视频中提取有用信息，并做出决策的学科。它通过模拟人类的视觉系统来识别、处理和理解视觉信息。主要任务：图像分类：识别图像中的物体并分类，比如猫、狗、车等。目标检测：在图像或视频中定位并识别多个对象，如人脸检测
  • 深度解析：如何使用输出解析器将大型语言模型（LLM）的响应解析为结构化JSON格式 m0_57781768 语言模型json人工智能
    深度解析：如何使用输出解析器将大型语言模型（LLM）的响应解析为结构化JSON格式在现代自然语言处理（NLP）的应用中，大型语言模型（LLM）已经成为了重要的工具。这些模型能够生成丰富的自然语言文本，适用于各种应用场景。然而，在某些应用中，开发者不仅仅需要生成文本，还需要将这些生成的文本转换为结构化的数据格式，例如JSON。这种结构化的数据格式在数据传输、存储以及进一步处理时具有显著优势。本文将深
  • 深入探讨：如何在Python中通过LangChain技术精准追踪大型语言模型（LLM）的Token使用情况 m0_57781768 pythonlangchain语言模型
    深入探讨：如何在Python中通过LangChain技术精准追踪大型语言模型（LLM）的Token使用情况在现代的人工智能开发中，大型语言模型（LLM）已经成为了不可或缺的工具，无论是用于自然语言处理、对话生成，还是其他复杂的文本生成任务。然而，随着这些模型的广泛应用，开发者面临的一个重要挑战是如何有效地追踪和管理Token的使用情况，特别是在生产环境中，Token的使用直接影响着API调用的成本
  • 使用最大边际相关性(MMR)选择示例：提高AI模型的多样性和相关性 aehrutktrjk 人工智能easyui前端python
    使用最大边际相关性(MMR)选择示例：提高AI模型的多样性和相关性引言在机器学习和自然语言处理领域，选择合适的训练示例对模型性能至关重要。最大边际相关性(MaximalMarginalRelevance,MMR)是一种优秀的示例选择方法，它不仅考虑了示例与输入的相关性，还注重保持所选示例之间的多样性。本文将深入探讨如何使用MMR来选择示例，以提高AI模型的性能和泛化能力。什么是最大边际相关性(MM
  • 使用LangChain和OpenAI实现高效文本标注 aehrutktrjk langchainpython
    使用LangChain和OpenAI实现高效文本标注引言在自然语言处理(NLP)领域，文本标注是一项重要且常见的任务。它涉及为文本分配标签，如情感、语言、风格等。本文将介绍如何使用LangChain和OpenAI的API来实现高效的文本标注系统。我们将探讨如何设置环境、定义标注模式，以及如何使用OpenAI的模型来执行标注任务。环境准备首先，我们需要安装必要的库并设置API密钥：%pipinsta
  • 【NLP5-RNN模型、LSTM模型和GRU模型】 一蓑烟雨紫洛 nlprnnlstmgrunlp
    RNN模型、LSTM模型和GRU模型1、什么是RNN模型RNN（RecurrentNeuralNetwork)中文称为循环神经网络，它一般以序列数据为输入，通过网络内部的结构设计有效捕捉序列之间的关系特征，一般也是以序列形式进行输出RNN的循环机制使模型隐层上一时间步产生的结果，能够作为当下时间步输入的一部分（当下时间步的输入除了正常的输入外还包括上一步的隐层输出）对当下时间步的输出产生影响2、R
  • 基于深度学习的文本引导的图像编辑 SEU-WYL 深度学习dnn深度学习人工智能
    基于深度学习的文本引导的图像编辑（Text-GuidedImageEditing）是一种通过自然语言文本指令对图像进行编辑或修改的技术。它结合了图像生成和自然语言处理（NLP）的最新进展，使用户能够通过描述性文本对图像内容进行精确的调整和操控。1.文本引导的图像编辑的挑战文本和图像之间的对齐：如何将文本中的语义信息准确地映射到图像中的特定区域或元素是一个关键挑战。这涉及到多模态数据的对齐和理解。编
  • 甘超波：NLP婚姻中如何与老人相处 甘超波
    哈喽，大家好我是甘超波，是一名NLP爱好者，每天一篇原创文章或视频，分享我的实战经验和案例，希望给你些启发和帮助看一下，在家庭中子女与老人观念不一致时案例1：在教育孩子方面，老人习惯用老一套教育方式教育孙子，子女受不了老人这种习惯，从而发生口舌之争？2：在生活习惯方面，老人喜欢吃剩菜剩饭，子女受不了老人这种习惯，从而发生口舌之争？.....这样的事情，我相信你或多或少都听过和看过，甚至了深有感悟。
  • 多模态Transformer之文本与图像联合建模 - Transformer教程 shandianfk_com ChatGPTTransformertransformer深度学习人工智能
    大家好，今天我们来聊聊一个既前沿又有趣的话题——多模态Transformer，特别是文本与图像的联合建模。对于很多小伙伴来说，Transformer这个词已经不陌生了，但它不仅仅应用于自然语言处理，还能在图像处理、甚至是多模态数据的处理上大显身手。接下来，我会带大家深入了解什么是多模态Transformer，以及它是如何实现文本与图像的联合建模的。Transformer简介首先，我们简单回顾一下T
  • 什么是AIGC？有哪些免费工具？ chent_某位 AIGC
    AIGC（AIGeneratedContent），即“人工智能生成内容”，是指通过人工智能技术自动生成各种类型的数字内容。AIGC让机器能够根据输入的信息或数据生成符合人类需求的文本、图像、音频、视频等内容，极大提高了内容创作的效率。AIGC的背景与起源随着深度学习和自然语言处理技术的快速发展，人工智能已经不再局限于简单的任务，如分类、预测和数据分析，而是具备了生成内容的能力。生成式AI模型，如O
  • transformer架构(Transformer Architecture)原理与代码实战案例讲解 AI架构设计之禅 大数据AI人工智能Python入门实战计算科学神经计算深度学习神经网络大数据人工智能大型语言模型AIAGILLMJavaPython架构设计AgentRPA
    transformer架构(TransformerArchitecture)原理与代码实战案例讲解关键词：Transformer,自注意力机制,编码器-解码器,预训练,微调,NLP,机器翻译作者：禅与计算机程序设计艺术/ZenandtheArtofComputerProgramming1.背景介绍1.1问题的由来自然语言处理（NLP）领域的发展经历了从规则驱动到统计驱动再到深度学习驱动的三个阶段。
  • 如何有效的学习AI大模型？ Python程序员罗宾 学习人工智能语言模型自然语言处理架构
    学习AI大模型是一个系统性的过程，涉及到多个学科的知识。以下是一些建议，帮助你更有效地学习AI大模型：基础知识储备：数学基础：学习线性代数、概率论、统计学和微积分等，这些是理解机器学习算法的数学基础。编程技能：掌握至少一种编程语言，如Python，因为大多数AI模型都是用Python实现的。理论学习：机器学习基础：了解监督学习、非监督学习、强化学习等基本概念。深度学习：学习神经网络的基本结构，如卷
  • 英伟达（NVIDIA）B200架构解读 weixin_41205263 芯际争霸GPGPU架构gpu算力人工智能硬件架构
    H100芯片是一款高性能AI芯片，其中的TransformerEngine是专门用于加速Transformer模型计算的核心部件。Transformer模型是一种自然语言处理（NLP）模型，广泛应用于机器翻译、文本生成等任务。TransformerEngine的电路设计原理主要包括以下几个方面：
  • 《昇思 25 天学习打卡营第 25 天 | 基于 MindSpore 实现 BERT 对话情绪识别 》 Sam9029 Mindscope模型学习深度学习
    《昇思25天学习打卡营第25天|基于MindSpore实现BERT对话情绪识别》活动地址：https://xihe.mindspore.cn/events/mindspore-training-camp签名：Sam9029环境配置确保安装了正确版本的MindSpore和MindNLP库。!pipuninstallmindspore-y!pipinstall-ihttps://pypi.mirror
  • 使用LangChain与Together AI模型交互：深入探讨和实践指南 llzwxh888 langchain人工智能交互python
    使用LangChain与TogetherAI模型交互：深入探讨和实践指南1.引言在人工智能和自然语言处理领域，TogetherAI已经成为一个强大的平台，提供了对50多个领先开源模型的访问。本文将深入探讨如何使用LangChain与TogetherAI模型进行交互，为开发者提供实用的知识和见解，同时解决可能遇到的常见问题。2.TogetherAI简介TogetherAI是一个强大的API平台，允许
  • OpenLM: 一个灵活的开源大语言模型接口工具 llzwxh888 语言模型人工智能自然语言处理python
    OpenLM:一个灵活的开源大语言模型接口工具引言在人工智能和自然语言处理快速发展的今天，大语言模型(LLM)已经成为许多应用的核心。然而，不同的LLM提供商往往有着各自的API和使用方式，这给开发者带来了一定的挑战。本文将介绍OpenLM，这是一个零依赖、兼容OpenAIAPI的LLM提供者接口，它可以直接通过HTTP调用不同的推理端点。我们将深入探讨OpenLM的特性、使用方法，以及如何将其与
  • 对股票分析时要注意哪些主要因素？ 会飞的奇葩猪 股票 分析 云掌股吧
    　　众所周知，对散户投资者来说，股票技术分析是应战股市的核心武器，想学好股票的技术分析一定要知道哪些是重点学习的，其实非常简单，我们只要记住三个要素：成交量、价格趋势、振荡指标。     一、成交量 　　大盘的成交量状态。成交量大说明市场的获利机会较多，成交量小说明市场的获利机会较少。当沪市的成交量超过150亿时是强市市场状态，运用技术找综合买点较准；
  • 【Scala十八】视图界定与上下文界定 bit1129 scala
    Context Bound，上下文界定，是Scala为隐式参数引入的一种语法糖，使得隐式转换的编码更加简洁。   隐式参数 首先引入一个泛型函数max，用于取a和b的最大值 def max[T](a: T, b: T) = { if (a > b) a else b }  因为T是未知类型，只有运行时才会代入真正的类型，因此调用a >
  • C语言的分支——Object-C程序设计阅读有感 darkblue086 applec框架cocoa
    自从1972年贝尔实验室Dennis Ritchie开发了C语言，C语言已经有了很多版本和实现，从Borland到microsoft还是GNU、Apple都提供了不同时代的多种选择，我们知道C语言是基于Thompson开发的B语言的，Object-C是以SmallTalk-80为基础的。和C++不同的是，Object C并不是C的超集，因为有很多特性与C是不同的。 Object-C程序设计这本书
  • 去除浏览器对表单值的记忆 周凡杨 html记忆autocompleteform浏览
                                       &n
  • java的树形通讯录 g21121 java
    最近用到企业通讯录，虽然以前也开发过，但是用的是jsf，拼成的树形，及其笨重和难维护。后来就想到直接生成json格式字符串，页面上也好展现。 // 首先取出每个部门的联系人 for (int i = 0; i < depList.size(); i++) { List<Contacts> list = getContactList(depList.get(i
  • Nginx安装部署 510888780 nginxlinux
    Nginx ("engine x") 是一个高性能的 HTTP 和 反向代理 服务器，也是一个 IMAP/POP3/SMTP 代理服务器。 Nginx 是由 Igor Sysoev 为俄罗斯访问量第二的 Rambler.ru 站点开发的，第一个公开版本0.1.0发布于2004年10月4日。其将源代码以类BSD许可证的形式发布，因它的稳定性、丰富的功能集、示例配置文件和低系统资源
  • java servelet异步处理请求 墙头上一根草 ｊａｖａ异步返回ｓｅｒｖｌｅｔ
    servlet3.0以后支持异步处理请求，具体是使用AsyncContext ，包装httpservletRequest以及httpservletResponse具有异步的功能，        final AsyncContext ac = request.startAsync(request, response);   ac.s
  • 我的spring学习笔记8-Spring中Bean的实例化 aijuans Spring 3
    在Spring中要实例化一个Bean有几种方法： 1、最常用的（普通方法） <bean id="myBean" class="www.6e6.org.MyBean" /> 使用这样方法，按Spring就会使用Bean的默认构造方法，也就是把没有参数的构造方法来建立Bean实例。 （有构造方法的下个文细说） 2、还
  • 为Mysql创建最优的索引 annan211 mysql索引
    索引对于良好的性能非常关键，尤其是当数据规模越来越大的时候，索引的对性能的影响越发重要。 索引经常会被误解甚至忽略，而且经常被糟糕的设计。 索引优化应该是对查询性能优化最有效的手段了，索引能够轻易将查询性能提高几个数量级，最优的索引会比 较好的索引性能要好2个数量级。 1 索引的类型 (1) B-Tree 不出意外，这里提到的索引都是指 B-
  • 日期函数 百合不是茶 oraclesql日期函数查询
      ORACLE日期时间函数大全 TO_DATE格式(以时间:2007-11-02 13:45:25为例) Year: yy two digits 两位年 显示值:07 yyy three digits 三位年 显示值:007
  • 线程优先级 bijian1013 javathread多线程java多线程
    多线程运行时需要定义线程运行的先后顺序。 线程优先级是用数字表示，数字越大线程优先级越高，取值在1到10，默认优先级为5。 实例： package com.bijian.study; /** * 因为在代码段当中把线程B的优先级设置高于线程A,所以运行结果先执行线程B的run()方法后再执行线程A的run()方法 * 但在实际中，JAVA的优先级不准，强烈不建议用此方法来控制执
  • 适配器模式和代理模式的区别 bijian1013 java设计模式
    一.简介        适配器模式：适配器模式（英语：adapter pattern）有时候也称包装样式或者包装。将一个类的接口转接成用户所期待的。一个适配使得因接口不兼容而不能在一起工作的类工作在一起，做法是将类别自己的接口包裹在一个已存在的类中。      &nbs
  • 【持久化框架MyBatis3三】MyBatis3 SQL映射配置文件 bit1129 Mybatis3
     SQL映射配置文件一方面类似于Hibernate的映射配置文件，通过定义实体与关系表的列之间的对应关系。另一方面使用<select>,<insert>,<delete>，<update>元素定义增删改查的SQL语句， 这些元素包含三方面内容 1. 要执行的SQL语句 2. SQL语句的入参，比如查询条件 3. SQL语句的返回结果
  • oracle大数据表复制备份个人经验 bitcarter oracle大表备份大表数据复制
    前提：    数据库仓库A（就拿oracle11g为例）中有两个用户user1和user2,现在有user1中有表ldm_table1,且表ldm_table1有数据5千万以上，ldm_table1中的数据是从其他库B（数据源）中抽取过来的，前期业务理解不够或者需求有变，数据有变动需要重新从B中抽取数据到A库表ldm_table1中。    
  • HTTP加速器varnish安装小记 ronin47 http varnish 加速
    上午共享的那个varnish安装手册，个人看了下，有点不知所云，好吧~看来还是先安装玩玩！ 苦逼公司服务器没法连外网，不能用什么wget或yum命令直接下载安装，每每看到别人博客贴出的在线安装代码时，总有一股羡慕嫉妒“恨”冒了出来。。。好吧，既然没法上外网，那只能麻烦点通过下载源码来编译安装了！ Varnish 3.0.4下载地址： http://repo.varnish-cache.org/
  • java-73-输入一个字符串，输出该字符串中对称的子字符串的最大长度 bylijinnan java
    public class LongestSymmtricalLength { /* * Q75题目：输入一个字符串，输出该字符串中对称的子字符串的最大长度。 * 比如输入字符串“google”，由于该字符串里最长的对称子字符串是“goog”，因此输出4。 */ public static void main(String[] args) { Str
  • 学习编程的一点感想 Cb123456 编程感想Gis
           写点感想，总结一些，也顺便激励一些自己.现在就是复习阶段，也做做项目.      本专业是GIS专业，当初觉得本专业太水，靠这个会活不下去的，所以就报了培训班。学习的时候，进入状态很慢，而且当初进去的时候，已经上到Java高级阶段了，所以.....，呵呵，之后有点感觉了，不过，还是不好好写代码，还眼高手低的，有
  • [能源与安全]美国与中国 comsci 能源
         现在有一个局面：地球上的石油只剩下N桶，这些油只够让中国和美国这两个国家中的一个顺利过渡到宇宙时代，但是如果这两个国家为争夺这些石油而发生战争，其结果是两个国家都无法平稳过渡到宇宙时代。。。。而且在战争中，剩下的石油也会被快速消耗在战争中，结果是两败俱伤。。。       在这个大
  • SEMI-JOIN执行计划突然变成HASH JOIN了 的原因分析 cwqcwqmax9 oracle
    甲说： A B两个表总数据量都很大，在百万以上。 idx1  idx2字段表示是索引字段 A B 两表上都有 col1字段表示普通字段 select xxx from A where A.idx1 between mmm and nnn      and exists (select 1 from B where B.idx2 =
  • SpringMVC-ajax返回值乱码解决方案 dashuaifu AjaxspringMVCresponse中文乱码
      SpringMVC-ajax返回值乱码解决方案   一：（自己总结，测试过可行） ajax返回如果含有中文汉字，则使用：（如下例：） @RequestMapping(value="/xxx.do")       public @ResponseBody void getPunishReasonB
  • Linux系统中查看日志的常用命令 dcj3sjt126com OS
    因为在日常的工作中，出问题的时候查看日志是每个管理员的习惯，作为初学者，为了以后的需要，我今天将下面这些查看命令共享给各位 cat tail -f 日 志 文 件 说 明 /var/log/message 系统启动后的信息和错误日志，是Red Hat Linux中最常用的日志之一 /var/log/secure 与安全相关的日志信息 /var/log/maillog 与邮件相关的日志信
  • [应用结构]应用 dcj3sjt126com PHPyii2
    应用主体 应用主体是管理 Yii 应用系统整体结构和生命周期的对象。 每个Yii应用系统只能包含一个应用主体，应用主体在 入口脚本中创建并能通过表达式 \Yii::$app 全局范围内访问。 补充: 当我们说"一个应用"，它可能是一个应用主体对象，也可能是一个应用系统，是根据上下文来决定[译：中文为避免歧义，Application翻译为应
  • assertThat用法 eksliang JUnitassertThat
    junit4.0  assertThat用法 一般匹配符1、assertThat( testedNumber, allOf( greaterThan(8), lessThan(16) ) ); 注释： allOf匹配符表明如果接下来的所有条件必须都成立测试才通过，相当于“与”（&&） 2、assertThat( testedNumber, anyOf( g
  • android点滴2 gundumw100 应用服务器android网络应用OSHTC
    如何让Drawable绕着中心旋转？ Animation a = new RotateAnimation(0.0f, 360.0f, Animation.RELATIVE_TO_SELF, 0.5f, Animation.RELATIVE_TO_SELF,0.5f); a.setRepeatCount(-1); a.setDuration(1000); 如何控制Andro
  • 超简洁的CSS下拉菜单 ini htmlWeb工作html5css
    效果体验：http://hovertree.com/texiao/css/3.htmHTML文件： <!DOCTYPE html> <html xmlns="http://www.w3.org/1999/xhtml"> <head> <title>简洁的HTML+CSS下拉菜单-HoverTree</title>
  • kafka consumer防止数据丢失 kane_xie kafkaoffset commit
    kafka最初是被LinkedIn设计用来处理log的分布式消息系统，因此它的着眼点不在数据的安全性（log偶尔丢几条无所谓），换句话说kafka并不能完全保证数据不丢失。   尽管kafka官网声称能够保证at-least-once，但如果consumer进程数小于partition_num，这个结论不一定成立。   考虑这样一个case，partiton_num=2
  • @Repository、@Service、@Controller 和 @Component mhtbbx DAOspringbeanprototype
    @Repository、@Service、@Controller 和 @Component 将类标识为Bean Spring 自 2.0 版本开始，陆续引入了一些注解用于简化 Spring 的开发。@Repository注解便属于最先引入的一批，它用于将数据访问层 (DAO 层 ) 的类标识为 Spring Bean。具体只需将该注解标注在 DAO类上即可。同时，为了让 Spring 能够扫描类
  • java 多线程高并发读写控制 误区 qifeifei java thread
    先看一下下面的错误代码，对写加了synchronized控制，保证了写的安全，但是问题在哪里呢？ public class testTh7 { private String data; public String read(){ System.out.println(Thread.currentThread().getName() + "read data "
  • mongodb replica set(副本集)设置步骤 tcrct javamongodb
    网上已经有一大堆的设置步骤的了，根据我遇到的问题，整理一下，如下： 首先先去下载一个mongodb最新版，目前最新版应该是2.6 cd /usr/local/bin wget http://fastdl.mongodb.org/linux/mongodb-linux-x86_64-2.6.0.tgz tar -zxvf mongodb-linux-x86_64-2.6.0.t
  • rust学习笔记 wudixiaotie 学习笔记
    1.rust里绑定变量是let，默认绑定了的变量是不可更改的，所以如果想让变量可变就要加上mut。 let x = 1; let mut y = 2; 2.match 相当于erlang中的case，但是case的每一项后都是分号，但是rust的match却是逗号。 3.match 的每一项最后都要加逗号，但是最后一项不加也不会报错，所有结尾加逗号的用法都是类似。 4.每个语句结尾都要加分
按字母分类： ABCDEFGHIJKLMNOPQRSTUVWXYZ其他