pytorch实现 minist 手写体分类任务
minist的分类任务在深度学习界属于hello world 级别的任务了,虽然任务简单,但是对入门来说还是相当重要的,这里采用pytorch来实现这个minist手写数字的分类任务
采用jupyter notebook的形式展现步骤
准备
1、环境中一定要准备好torch,对于项目项目的其他模块 如果没有直接采用 pip install 命令 安装即可
import torch
print(torch.__version__)
1.12.1
2、图表嵌入
使用%matplotlib命令可以将matplotlib的图表直接嵌入到Notebook之中,或者使用指定的界面库显示图表,它有一个参数指定matplotlib图表的显示方式。inline表示将图表嵌入到Notebook中。
%matplotlib inline
3、准备数据集,如果数据集不存在就在脚本目录下新建 data/minist目录下载数据集
from pathlib import Path
import requests
DATA_PATH = Path("data")
PATH = DATA_PATH / "mnist"
PATH.mkdir(parents=True, exist_ok=True)
URL = "http://deeplearning.net/data/mnist/"
FILENAME = "mnist.pkl.gz"
if not (PATH / FILENAME).exists():
content = requests.get(URL + FILENAME).content
(PATH / FILENAME).open("wb").write(content)
4、读取数据集,将分为 训练集((x_train, y_train)) 、验证集 ( (x_valid, y_valid))两部分
import pickle
import gzip
with gzip.open((PATH / FILENAME).as_posix(), "rb") as f:
((x_train, y_train), (x_valid, y_valid), _) = pickle.load(f, encoding="latin-1")
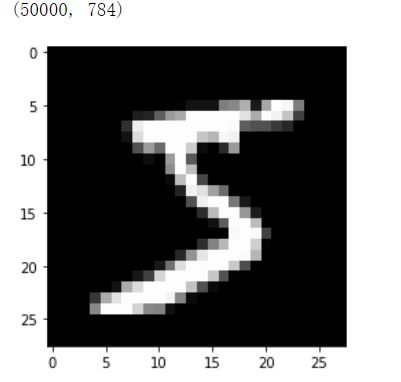
5、看看训练集 的第一个数据是什么样子的
from matplotlib import pyplot
import numpy as np
print(x_train.shape) #打印训练集的大小
pyplot.imshow(x_train[0].reshape((28, 28)), cmap="gray")
# 将训练集的 784个像素点重排列成28*28的图像 打印出来(注意这里没有赋值,不会影响到原数据本身)
构建模型
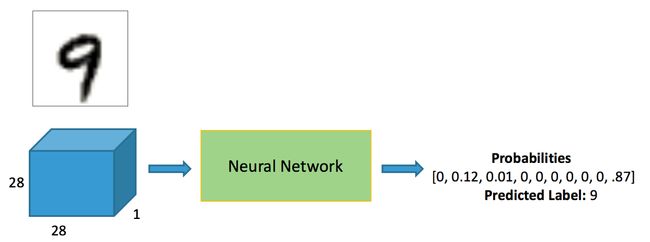
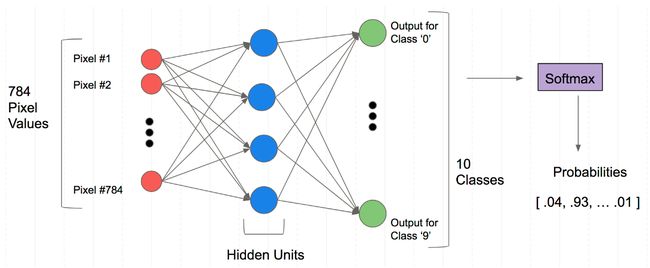
输入时一个784 的 对应着 每一个图像的维度(红色)
中间隐藏层 可以设置多层(上图中只画了一层 蓝色)
最后由于是十分类的任务,将输出神经元个数 (绿色)
6、 将数据转换为 tensor 格式,因为 torch的模型训练过程都是基于 tensor 的数据 ,它能够自动的帮助我们实现反向传播过程
import torch
x_train, y_train, x_valid, y_valid = map(
torch.tensor, (x_train, y_train, x_valid, y_valid)
) # 这里通过 函数 tensor数据map(torch.tensor, 原数据) 文成对数据的映射操作
n, c = x_train.shape
x_train, x_train.shape, y_train.min(), y_train.max()
print(x_train, y_train)
print(x_train.shape)
print(y_train.min(), y_train.max())
下面是执行结果
tensor([[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
...,
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.]]) tensor([5, 0, 4, ..., 8, 4, 8])
torch.Size([50000, 784])
tensor(0) tensor(9)
7、 模型搭建
from torch import nn
class Mnist_NN(nn.Module):
def __init__(self):
super().__init__()
self.hidden1 = nn.Linear(784, 128)
self.hidden2 = nn.Linear(128, 256)
self.out = nn.Linear(256, 10)
self.dropout = nn.Dropout(0.5)
def forward(self, x): # x 是输入数据 64 *784 64 是batch大小
# 注意 torch 训练时 一般都是一个batch 一个 batch的输入 batch大小由 dataLoader函数指定
x = F.relu(self.hidden1(x)) # 64 *128 这里实现的时输入到隐藏层神经元数据的映射
x = self.dropout(x) #
x = F.relu(self.hidden2(x)) # 另一个隐藏层
x = self.dropout(x) #
x = self.out(x)
return x
打印模型
net = Mnist_NN()
print(net)
Mnist_NN(
(hidden1): Linear(in_features=784, out_features=128, bias=True)
(hidden2): Linear(in_features=128, out_features=256, bias=True)
(out): Linear(in_features=256, out_features=10, bias=True)
(dropout): Dropout(p=0.5, inplace=False)
)
可以通过 模型名字.named_parameters() 打印模型中的各种参数的数据
权重参数一开始一般都是模型随机生成的,没有什么实际意义,主要看的是这些参数的shape
for name, parameter in net.named_parameters():
print(name, parameter,parameter.size())
hidden1.weight Parameter containing:
tensor([[ 1.3390e-02, -1.5857e-02, -7.1516e-04, ..., -1.8079e-02,
1.5434e-02, 2.7576e-02],
[ 7.9442e-03, -1.1649e-02, -3.3914e-02, ..., -2.9112e-02,
-2.9767e-04, -3.4292e-02],
[-7.8026e-03, 2.3379e-02, -1.0540e-02, ..., 3.5679e-02,
1.8505e-02, 3.0153e-02],
...,
[-1.1630e-02, 1.5202e-02, 3.0876e-02, ..., -1.9012e-02,
2.0537e-02, -9.2316e-03],
[-8.4422e-03, -2.0339e-02, 3.1877e-02, ..., -3.0178e-02,
2.4106e-02, -2.3417e-02],
[ 2.3607e-03, 2.1591e-02, 3.0494e-02, ..., 2.6278e-02,
-2.6456e-02, 3.9756e-05]], requires_grad=True) torch.Size([128, 784])
hidden1.bias Parameter containing:
tensor([-0.0231, -0.0269, 0.0183, 0.0143, 0.0262, -0.0005, -0.0277, 0.0070,
-0.0309, 0.0351, 0.0284, 0.0163, 0.0338, -0.0328, -0.0098, -0.0338,
0.0091, -0.0230, 0.0262, 0.0316, -0.0203, -0.0220, -0.0012, -0.0240,
-0.0078, -0.0353, -0.0190, 0.0021, 0.0050, -0.0173, 0.0324, -0.0021,
-0.0008, 0.0227, 0.0252, 0.0131, -0.0336, -0.0039, 0.0068, 0.0253,
0.0252, -0.0342, 0.0060, 0.0156, 0.0308, -0.0164, -0.0210, -0.0244,
-0.0073, 0.0313, -0.0172, -0.0345, 0.0064, -0.0260, -0.0096, -0.0258,
-0.0218, 0.0259, -0.0134, -0.0188, 0.0218, 0.0030, 0.0191, -0.0197,
-0.0337, 0.0087, -0.0113, 0.0091, 0.0075, -0.0225, -0.0209, -0.0196,
0.0085, -0.0005, 0.0032, -0.0014, 0.0293, 0.0242, -0.0238, -0.0343,
-0.0003, -0.0131, -0.0209, -0.0186, -0.0091, -0.0010, -0.0349, 0.0312,
-0.0259, -0.0276, -0.0250, 0.0024, 0.0038, 0.0027, 0.0097, 0.0109,
-0.0011, 0.0347, -0.0318, -0.0320, -0.0123, 0.0351, 0.0245, -0.0352,
0.0125, 0.0216, -0.0205, 0.0111, 0.0139, 0.0238, -0.0074, 0.0156,
-0.0296, 0.0069, -0.0062, 0.0304, 0.0056, -0.0331, 0.0011, 0.0181,
0.0067, 0.0323, 0.0019, -0.0353, 0.0117, -0.0320, 0.0082, 0.0157],
requires_grad=True) torch.Size([128])
hidden2.weight Parameter containing:
tensor([[-0.0292, 0.0668, 0.0180, ..., 0.0638, 0.0365, -0.0806],
[-0.0453, 0.0683, -0.0168, ..., 0.0742, -0.0197, -0.0044],
[-0.0706, -0.0204, -0.0646, ..., -0.0337, 0.0381, 0.0224],
...,
[ 0.0189, -0.0351, -0.0503, ..., 0.0809, -0.0232, -0.0300],
[ 0.0787, 0.0404, -0.0860, ..., -0.0521, -0.0537, 0.0269],
[ 0.0776, 0.0439, -0.0874, ..., -0.0616, 0.0108, -0.0066]],
requires_grad=True) torch.Size([256, 128])
hidden2.bias Parameter containing:
tensor([-0.0179, 0.0424, -0.0011, 0.0221, 0.0126, 0.0451, -0.0424, -0.0524,
-0.0080, 0.0400, -0.0512, -0.0701, 0.0639, 0.0821, -0.0208, -0.0594,
-0.0878, 0.0477, -0.0226, 0.0346, -0.0100, -0.0544, 0.0412, 0.0461,
0.0462, -0.0792, -0.0041, -0.0179, -0.0391, 0.0422, 0.0360, -0.0649,
-0.0405, 0.0009, 0.0273, 0.0417, -0.0277, 0.0760, 0.0467, -0.0658,
-0.0525, 0.0323, 0.0411, 0.0214, 0.0328, -0.0642, -0.0418, 0.0304,
0.0096, -0.0443, 0.0273, -0.0776, 0.0641, -0.0498, -0.0203, 0.0192,
0.0586, -0.0192, -0.0584, 0.0659, 0.0762, -0.0634, -0.0432, 0.0146,
-0.0627, 0.0112, -0.0745, -0.0247, -0.0679, -0.0434, 0.0697, 0.0658,
-0.0330, 0.0744, -0.0368, 0.0526, -0.0308, -0.0032, 0.0774, -0.0195,
-0.0869, -0.0180, 0.0399, 0.0418, -0.0653, -0.0406, -0.0406, 0.0555,
0.0348, 0.0251, 0.0225, 0.0629, 0.0202, -0.0840, -0.0576, -0.0532,
0.0031, 0.0772, -0.0811, 0.0468, 0.0027, -0.0329, 0.0362, 0.0632,
-0.0544, 0.0580, 0.0136, -0.0274, -0.0124, 0.0626, -0.0051, -0.0735,
0.0740, 0.0322, -0.0709, -0.0674, -0.0509, 0.0377, -0.0169, -0.0715,
-0.0745, 0.0751, -0.0567, -0.0312, 0.0103, 0.0099, 0.0704, -0.0822,
-0.0562, -0.0875, 0.0030, 0.0066, 0.0791, -0.0710, 0.0269, 0.0076,
0.0179, -0.0228, -0.0527, 0.0125, 0.0534, 0.0251, -0.0573, -0.0238,
-0.0010, -0.0588, 0.0771, -0.0303, -0.0497, -0.0616, 0.0536, -0.0544,
-0.0263, 0.0130, -0.0624, -0.0556, 0.0091, 0.0217, 0.0514, 0.0722,
-0.0726, -0.0007, 0.0640, 0.0341, -0.0409, 0.0748, -0.0478, 0.0353,
-0.0208, 0.0809, -0.0599, 0.0394, 0.0595, 0.0481, -0.0725, 0.0633,
0.0388, -0.0181, -0.0525, 0.0503, 0.0338, 0.0154, 0.0495, -0.0468,
-0.0355, 0.0218, 0.0361, -0.0038, -0.0060, -0.0832, 0.0192, 0.0616,
0.0160, -0.0578, -0.0652, 0.0858, 0.0859, -0.0460, -0.0466, -0.0731,
0.0475, -0.0061, -0.0029, 0.0586, -0.0853, 0.0151, -0.0264, 0.0849,
0.0586, 0.0273, -0.0388, -0.0114, 0.0511, 0.0138, 0.0849, -0.0010,
0.0500, -0.0125, -0.0270, -0.0495, 0.0079, 0.0510, 0.0820, 0.0564,
-0.0291, -0.0189, 0.0470, -0.0020, -0.0539, -0.0464, 0.0194, -0.0609,
-0.0739, -0.0512, -0.0694, 0.0802, -0.0193, 0.0207, 0.0350, 0.0600,
-0.0666, -0.0740, 0.0250, 0.0096, -0.0151, -0.0610, -0.0481, -0.0059,
0.0709, -0.0606, -0.0510, 0.0401, -0.0569, -0.0752, 0.0163, 0.0571],
requires_grad=True) torch.Size([256])
out.weight Parameter containing:
tensor([[-0.0335, -0.0395, -0.0313, ..., 0.0609, 0.0167, 0.0246],
[ 0.0061, 0.0312, 0.0201, ..., 0.0031, 0.0564, 0.0077],
[-0.0461, -0.0233, -0.0534, ..., -0.0535, -0.0399, -0.0293],
...,
[ 0.0098, 0.0508, 0.0563, ..., -0.0531, -0.0513, -0.0597],
[ 0.0418, -0.0037, 0.0404, ..., 0.0225, -0.0026, -0.0314],
[-0.0493, -0.0155, -0.0173, ..., 0.0320, -0.0611, 0.0176]],
requires_grad=True) torch.Size([10, 256])
out.bias Parameter containing:
tensor([ 0.0594, 0.0460, 0.0581, -0.0160, -0.0477, -0.0608, 0.0384, 0.0355,
-0.0373, 0.0061], requires_grad=True) torch.Size([10])
读取数据 (采用 TensorDataset和DataLoader来简化)
torch 中的 Dataset 和 DataLoader 对于输入数据的处理整理并读取是两个非常重要的函数,前者作用一般将数据和标签对应好, 后者主要指定数据的batchsize 还有是否打乱等,
这两个函数 需要花很多时间去l理解掌握,这里不详细展开
8、数据集读取
from torch.utils.data import TensorDataset
from torch.utils.data import DataLoader
bs = 64 # batch size
train_ds = TensorDataset(x_train, y_train)
train_dl = DataLoader(train_ds, batch_size=bs, shuffle=True)
valid_ds = TensorDataset(x_valid, y_valid)
valid_dl = DataLoader(valid_ds, batch_size=bs * 2)
定义获取数据的函数
def get_data(train_ds, valid_ds, bs):
return (
DataLoader(train_ds, batch_size=bs, shuffle=True),
DataLoader(valid_ds, batch_size=bs * 2),
)
9、模型训练
一般在训练模型时加上model.train(),这样会正常使用Batch Normalization和 Dropout
测试的时候一般选择model.eval(),这样就不会使用Batch Normalization和 Dropout
import numpy as np
def fit(steps, model, loss_func, opt, train_dl, valid_dl):
for step in range(steps):
model.train()
for xb, yb in train_dl:
loss_batch(model, loss_func, xb, yb, opt)
model.eval()
with torch.no_grad():
losses, nums = zip(
*[loss_batch(model, loss_func, xb, yb) for xb, yb in valid_dl]
# zip 用来数据大包整一个元组,zip(* 数据 ) 这用具再将数据的元组打开
)
val_loss = np.sum(np.multiply(losses, nums)) / np.sum(nums)
print('当前step:'+str(step), '验证集损失:'+str(val_loss))
10、 获取模型以及优化器
from torch import optim
def get_model():
model = Mnist_NN()
return model, optim.SGD(model.parameters(), lr=0.001)
11、定义损失
def loss_batch(model, loss_func, xb, yb, opt=None):
loss = loss_func(model(xb), yb)
if opt is not None:
loss.backward()
opt.step()
opt.zero_grad()
return loss.item(), len(xb)
12 、 训练
train_dl, valid_dl = get_data(train_ds, valid_ds, bs)
model, opt = get_model()
fit(25, model, loss_func, opt, train_dl, valid_dl)
当前step:0 验证集损失:2.281765052032471
当前step:1 验证集损失:2.2548073917388916
当前step:2 验证集损失:2.2168532493591306
当前step:3 验证集损失:2.1594999446868894
当前step:4 验证集损失:2.071791256713867
当前step:5 验证集损失:1.9400685039520265
当前step:6 验证集损失:1.7583607305526734
当前step:7 验证集损失:1.5454200302124024
当前step:8 验证集损失:1.336092336654663
当前step:9 验证集损失:1.161786738395691
当前step:10 验证集损失:1.0268419866561889
当前step:11 验证集损失:0.9225819948196411
当前step:12 验证集损失:0.841665417098999
当前step:13 验证集损失:0.7782670201301575
当前step:14 验证集损失:0.7254350215911866
当前step:15 验证集损失:0.680208807182312
当前step:16 验证集损失:0.6434079674720764
当前step:17 验证集损失:0.6106972219467163
当前step:18 验证集损失:0.5825114577293397
当前step:19 验证集损失:0.558058225440979
当前step:20 验证集损失:0.5358199080467224
当前step:21 验证集损失:0.5162367730140686
当前step:22 验证集损失:0.5001176020145416
当前step:23 验证集损失:0.48417559719085695
当前step:24 验证集损失:0.4703081311225891