关于S/N、Eb/N0 、Es/N0 的关系
一、从“数据比特”到“符号”再到“采样点”
探讨题目中SNR、Eb/N0 、Es/N0 的关系,必须要对“数据比特”到“符号”再到“采样点”这数据的三种形态有清楚的认知,明白各个参量在发送端处于什么样的位置/状态。
首先是数据比特(信息比特),就是我们想要传输的二进制数据 ,速率(信息速率)为 R b R_{b} Rb
数据比特需要经过信道编码、多进制映射变成一个个 符号(信道符号),速率(符号速率)为 R s R_{s} Rs
这些符号经过 (上)采样(采样速率往往是符号速率的整数倍)得到采样点,速率为采样速率 f s f_{s} fs
下图为三种数据状态的关系
(1)、数据比特 到 符号:
我们定义 变量 k k k 为:一个符号对应的数据比特的数量 。 即 k = R b R s k=\frac{R_{b}}{R_{s}} k=RsRb
如果数据比特到符号要经过码率为 R R R的信道编码,以及 M M M进制的调制,易得 k = R ⋅ l o g 2 M k=R\cdot log_{2}M k=R⋅log2M
如:数据比特经过了码率为4/7的汉明码,以及4进制的QPSK调制,那么 k = 4 7 ⋅ l o g 2 4 = 8 7 k=\frac{4}{7}\cdot log_{2}4=\frac{8}{7} k=74⋅log24=78
(2)、符号 到 采样点:
定义变量:sps(sample per symbol)为,每个 符号 对应的采样点数,或者说每个符号采几次样。 即 s p s = f s R s sps=\frac{f_{s}}{R_{s}} sps=Rsfs
则易得: f s R b = s p s k \frac{f_{s}}{R_{b}}=\frac{sps}{k} Rbfs=ksps
二、S/N、Eb/N0 、Es/N0 的关系
在模拟通信中SNR是一个衡量信噪比常用的指标,但在数字通信系统中,我们将传输的数据分割成一个个码元,用码元能量 E s E_{s} Es,码元速率 R s R_{s} Rs来描述一个离散的数据系统更为妥当。鉴于不同系统采用的编码方式以及调制方式不同,为了统一,在 比特级(比特能量 E b E_{b} Eb,比特速率 R b R_{b} Rb) 角度来分析信噪比更为“公平”。
(1)、S/N 到 Es/N0
根据定义S/N是信号功率与 E s ⋅ R s E_{s}\cdot R_{s} Es⋅Rs 噪声功率 N 0 ⋅ W N_{0}\cdot W N0⋅W之比,即
S N = E s ⋅ R s N 0 ⋅ W \frac{S}{N}=\frac{E_{s}\cdot R_{s}}{N_{0}\cdot W} NS=N0⋅WEs⋅Rs 注意:
- (1) N 0 N_{0} N0为高斯白噪声功率谱密度,这是相对于复信号来说的;对于实信号,功率谱密度为 N 0 / 2 N_{0}/2 N0/2。
- (2) W W W为信号带宽,常常用 f s f_{s} fs替代,(这是为什么?有知道的小伙伴可以在评论区留言)
那么;
S N = E s ⋅ R s N 0 ⋅ f s = E s N 0 ⋅ 1 s p s \frac{S}{N}=\frac{E_{s}\cdot R_{s}}{N_{0}\cdot f_{s}}=\frac{E_{s}}{N_{0}}\cdot \frac{1}{sps} NS=N0⋅fsEs⋅Rs=N0Es⋅sps1
(2)、 Es/N0 到 Eb/N0
由于一个信号的功率S可以表示为
S = E s ⋅ R s = E b ⋅ R b S=E_{s}\cdot R_{s}=E_{b}\cdot R_{b} S=Es⋅Rs=Eb⋅Rb
由第一节中Rs与Rb的关系,则可以得到
E s E b = k \frac{E_{s}}{E_{b}}=k EbEs=k
E s N 0 = E b N 0 ⋅ k \frac{E_{s}}{N_{0}}=\frac{E_{b}}{N_{0}}\cdot k N0Es=N0Eb⋅k
则易得: S N = E b N 0 ⋅ k s p s \frac{S}{N}=\frac{E_{b}}{N_{0}} \cdot \frac{k}{sps} NS=N0Eb⋅spsk
至此我们得到了S/N与Eb/N0的关系;
三、在仿真工作中如何应用?(以matlab为例)
仿真过程中一般画的都是Eb/N0(dB)为横轴的误码率曲线图,如图
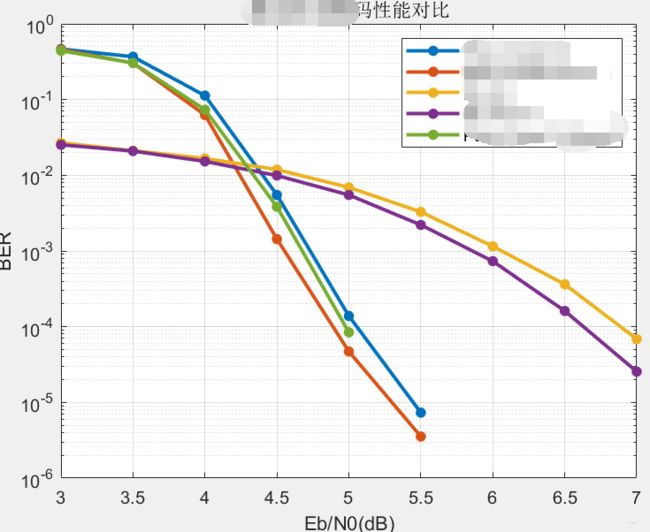
这里的应用就是将Eb/N0(dB)转化为S/N在添加,再根据S/N添加高斯白噪声。
在matlab中添加高斯白噪声的方式有两种:
无论哪种都得先将Eb/N0转化为S/N:
由于 S N = E b N 0 ⋅ k s p s \frac{S}{N}=\frac{E_{b}}{N_{0}} \cdot \frac{k}{sps} NS=N0Eb⋅spsk所以,
S N ( d B ) = E b N 0 ( d B ) + 10 ⋅ l o g 10 k s p s \frac{S}{N} (dB)=\frac{E_{b}}{N_{0}}(dB)+10\cdot log_{10} \frac{k}{sps} NS(dB)=N0Eb(dB)+10⋅log10spsk
matlab实现
snrdB=ebn0dB+10*log10(k/sps);
- 1 matlab自带awgn()函数
具体用法我就不详细说了,大家 用help awgn命令看看就好
signal_addnoise=awgn(your_signal,snrdB,'measured');
注意:这里的yoursignal 是采样过后的信号,下同。
- 2 用随机序列模拟
由S/N (dB)的定义 s n r ( d B ) = 10 ⋅ l g S N snr(dB)=10\cdot lg \frac{S}{N} snr(dB)=10⋅lgNS易得:
N = σ 2 = S × 1 0 − S N ( d B ) 10 N=\sigma ^{2}=S×10^{-\frac{\frac{S}{N} (dB)}{10}} N=σ2=S×10−10NS(dB)
N=(sum(yoursignal.^2)/length(yoursignal)) * 10^(-snrdB/10);
S是采样点的平均能量,N是采样点平均噪声能量,求得N以后,可以按照以下代码添加噪声
signal_addnoise=your_signal+randn(size(your_signal)).*sqrt(N/2)+1i*randn(size(your_signal)).*sqrt(N/2);
注意,这里我都是默认信号为复信号,如果是实信号,实现方式又是怎样呢?
附加:实信号推导
实信号的话,推导应该从哪里开始变化的呢?
我其实已经在文章中写了,在第二节,第一小节中,实信号功率谱密度应该把 N 0 N_0 N0替换为 N 0 2 \frac{N_0}{2} 2N0,那么
S N = E s N 0 ⋅ 2 s p s = E b N 0 ⋅ 2 ⋅ k s p s \frac{S}{N}=\frac{E_{s}}{N_{0}}\cdot \frac{2}{sps}=\frac{E_{b}}{N_{0}}\cdot \frac{2\cdot k}{sps} NS=N0Es⋅sps2=N0Eb⋅sps2⋅k
所以,
S N ( d B ) = E b N 0 ( d B ) + 10 ⋅ l o g 10 2 ⋅ k s p s \frac{S}{N} (dB)=\frac{E_{b}}{N_{0}}(dB)+10\cdot log_{10} \frac{2 \cdot k}{sps} NS(dB)=N0Eb(dB)+10⋅log10sps2⋅k
snrdB=ebn0dB+10*log10(2*k/sps);
- 1 matlab 自带awgn函数
signal_addnoise=awgn(your_signal,snrdB,'measured');
- 2 用随机序列模拟
由S/N (dB)的定义 s n r ( d B ) = 10 ⋅ l g S N snr(dB)=10\cdot lg \frac{S}{N} snr(dB)=10⋅lgNS易得:
N = σ 2 = S × 1 0 − S N ( d B ) 10 N=\sigma ^{2}=S×10^{-\frac{\frac{S}{N} (dB)}{10}} N=σ2=S×10−10NS(dB)
N=(sum(yoursignal.^2)/length(yoursignal)) * 10^(-snrdB/10);
S是采样点的平均能量,N是采样点平均噪声能量,求得N以后,可以按照以下代码添加噪声
signal_addnoise=your_signal+randn(size(your_signal)).*sqrt(N);
