知识蒸馏在目标检测中的应用

知识蒸馏在目标检测中的应用

Knowledge Distillation

日常训练中，我们往往使用复杂的模型，大量的计算资源，以便于能够从非常大，高度冗余的数据中提取信息。假如我们已经训练好一个复杂的模型，要想部署到服务器或者设备上，则对部署资源要求比较高，而且推理时间会相对很慢。但是在实际应用中，部署对时延和计算资源都有很高的要求。各种对模型瘦身的方法也都陆续出现，比如模型压缩，模型量化等等。

知识蒸馏是一种模型压缩的算法，它训练小模型去模仿一个已经训练好的大模型或者集合模型。有时候这种训练方式被认为是“teacher-student”模式，大而笨重的模型被称为“teacher”，小而轻巧的模型被称为“student”。一旦大模型训练完成，我们就可以使用一种特殊的训练方式，将大模型中的知识转移到便于模型的小模型中，这种方式被称为“蒸馏”。

Soft Target vs Hard Target

一种将大模型的通用能力转换到小模型中的方法是将大模型的类别概率作为“soft target”去训练小模型。当soft target 具有较高的熵时，在训练阶段，soft target能够比hard target提供更多的信息和训练案例间更小的方法，那么小模型通常就可以在比大模型少得多的数据上进行训练，并且可以使用更高的学习率。

比如，在MNIST任务中，大模型通常能够以高置信度得到正确的答案，但是学习到的大部分信息都存在于soft target极小概率的比率中。加入某个输入的“2”更加形似“3”，而某个“2”更加形似“7”。如果用hard target（0，1）来表示，它们的值是相同的；但是用soft target表示，它们分数值有所不同。“2”与“3”相似，除“2”的概率值之外，“3”的概率值要比其他数的值高，同理，“2”与“7”相似，那么“7”的概率值要比其他数的值高。如下图所示，而且soft target分布的熵要相对高些，其包含的知识也就更丰富。

Distillation

神经网络通常由一个softmax函数$q_i=\frac{exp\left(z_i\right)}{{\sum }_{j}exp\left(z_j\right)}$输出类别分类，为了提供类别之间的soft概率分布，将原softmax函数加以修改，如下所示：
$$q_j=\frac{exp\left(z_i/T\right)}{{\sum }_{j}exp\left(z_j/T\right)}$$
其中参数$T$表示“温度”。当$T=1$，为原softmax函数。$T$值越高，softmax的输出概率分布区域越平滑（softer），输出概率分布也提供更多teacher模型发现的与预测类别相似的类别信息，论文作者Hinton称其为镶嵌在teacher模型中的“dark knowledge”。简单的蒸馏形式是：对大模型上的softmax使用较高的温度，生产出tranfer set中每一个实例的soft target 分布，然后通过训练transfer set，将知识转移到小模型中。当训练小模型时，需要相同的温度。当小模型训练完成后，它的温度将设为1。

如下图所示，小模型训练时，目标函数由两个子目标函数组成，第一个目标函数是soft target和soft label的交叉熵函数，小模型和大模型使用相同的温度。第二个目标函数是小模型原交叉熵目标函数。

Faster RCNN

Faster RCNN包含三个子模型，一个卷积网络提取特征，一个region proposal network(RPN)生成候选框和一个分类和回归网络（RCN），输出分类结果和候选框信息。我们回想一下Faster RCNN的损失函数：
$$L\left(\left\{p_i\right\},\left\{t_i\right\}\right)=\frac{1}{N_{cls}}\sum _i{L}_{cls}\left\{p_i,p_i^{\ast }\right\}+\lambda \frac{1}{N_{reg}}\sum _i{p}_i^{\ast }{L}_{reg}\left(t_i,t_i^{\ast }\right)$$

Learning Efficient Object Detection Models with Knowledge Distillation

在多类别目标检测领域实施蒸馏技术，相对于图像分类，有如下几种挑战：

1. 由于检测标签更加昂贵并且体积更小，检测性能的性能会因为压缩而受到更大的影响。
2. 假设每一类别都是同等重要的，知识蒸馏被提出用于分类。但是对于背景类别更加普通的检测，则不是这样的。
3. 检测相比于分类，是更复杂的任务。检测包括分类和bbox回归。
4. 我们讲重点放在一个领域内的知识传输，不需要额外的数据或标签。反对可能依赖来自于其他域的数据工作。

Overall Structure

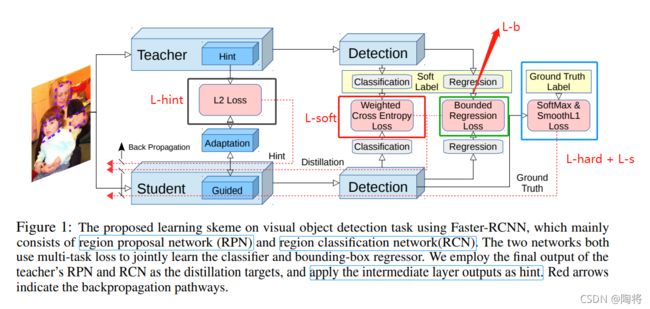
《Learning Efficient Object Detection Models with Knowledge Distillation》是第一篇将知识蒸馏用到多类别目标检测中的论文。论文中提出一种端到端的网络应用知识蒸馏学习紧凑的多类别目标检测模型。模型整体建构如下图所示：

• 首先，我们采用学校到的线索（the hint based learning）鼓励student网络的特征表达相似于teacher 网络。
• 再者，我们使用知识蒸馏框架在RPN和RCN模块中学习更强的分类模型。为了解决目标检测种类别不平衡问题，我们为蒸馏网络使用了weighted cross entropy loss。
• 最后，我们将teacher的回归输出转换为上界的一种形式（a form of upper bound）。那也就是说，如果一个学生的回归输出比teacher的回归输出要好，那么没有额外的loss应用了。

那么总目标函数就可以如下所示：

$$\begin{array}{c}{L}_{RCN}=\frac{1}{N}{\sum }_i{L}_{cls}^{RCN}+\lambda \frac{1}{N}{\sum }_j{L}_{reg}^{RCN}\\ L_{RPN}=\frac{1}{M}{\sum }_i{L}_{cls}^{RPN}+\lambda \frac{1}{M}{\sum }_j{L}_{reg}^{RPN}\\ L=L_{RPN}+L_{RCN}+\gamma L_{Hint}\end{array}$$

其中$N$是RCN的批次大小，$M$是RPN的批次大小。$L_{cls}$是分类损失函数；$L_{reg}$ 是bbox回归损失函数；$L_{hint}$表示鼓励student模仿teacher特征反馈的线索损失函数。其中参数$\lambda$和$\gamma$是能够平衡不同损失函数的超参数。

KD for cls with Imbalanced Classes

假设有数据集$\left(x_i,y_i\right),i=1,2,\cdots ,n$，其中$x_i\in \chi$是输入图像，$y_i\in \varsigma$是类型标签。

$t$是teacher 模型，$Z_t$是最后score输出，预测值$P_t=softmax\left(\frac{Z_t}{T}\right)$，相似地，$s$是student模型，预测值为$P_s=softmax\left(\frac{Z_s}{T}\right)$，那么student $s$在训练时被优化的损失函数如下所示：

$$L_{cls}=\mu L_{hard}\left(P_s,y\right)+\left(1-\mu \right)L_{soft}\left(P_s,P_t\right)$$

$L_{hard}$是hard loss损失函数，使用Faster RCNN中的gt 标签，和Faster RCNN中的分类损失函数一样；$L_{soft}$是soft损失函数，是使用teacher网络的预测值；$\mu$是平衡hard 和soft损失函数的参数。soft 标签涵盖teacher网络没有发现的不同类别之间的关系信息，从soft标签中，student网络能够继承到这些隐藏的信息。hard和soft损失函数都是交叉熵函数，不同于简单的分类问题，检测问题需要解决不同类别之间的不平衡问题。分类问题，分类错误仅仅出现在前景类别中，但是在检测问题中，前景和背景都能够导致分类错误，并且前景分类错误的频率是稀少的。为了解决这个问题，论文中采用adopt class-weighted cross entropy 作为蒸馏损失函数。

$$L_{soft}\left(P_s,P_t\right)=-\sum {\omega }_c{P}_{t}Log{P}_s$$

对于背景类别，采用较大的权重；对于其他类别，则采用较小的权重。比如在PASCAL数据集中，对背景类别则定义${\omega }_0=1.5$，对于其他类别，设置${\omega }_i=1$。

$P_t$和hard label相似，对一个类别的概率非常接近于1，大多数其他的概率接近于0，温度参数$T$的引用则soften输出。使用较高的温度将会迫使teacher 模型$t$输出softer labels，以至于概率接近于0的类别将不会被loss函数忽略。对于简单的任务，比如手写字分类，是非常适当的。但是对于更难的问题，一个比较大的温度值$T$产生更多的噪音，不利于学习，导致预测错误是非常高的。因此，在大型数据集上的分类，需要较低的$T$值。甚至对于更难的问题，比如目标检测，在蒸馏损失函数中不使用温度参数值$T=1$在实际应用中，性能最优。

KD for Regression with Teacher Bounds

在目标检测中，bbox回归需要调整物体的位置和大小信息，对检测的准确率至关重要。不像学习离散类别的蒸馏模型，由于实数值回归输出是无界限的，teacher模型的回归输出可能会向student模型提供错误的导向，也许teacher模型的回归输出和真实方向相反呢。因此，为了避免直接以teacher模型的回归输出为导向，论文中提出了将teacher模型的回归输出作为student模型的上界。一般来说，student模型的输出向量要尽可能地接近gt标签，但是如果一旦student模型的输出向量超过teacher模型输出加上特定一个margin值的和，那么对于此student模型，不需要额外的损失函数。论文称此损失函数为teacher bounded regression loss,$L_b$。那么回归的损失函数如下所示：

$$\begin{array}{c}{L}_b\left(R_s,R_t,y\right)=\{\begin{array}{cc}\Vert R_s-y{\Vert }_2^2,& if\Vert R_s-y{\Vert }_2^2+m>\Vert R_t-y{\Vert }_2^2\\ 0,& othersize\end{array}\\ L_{reg}=L_{s{L}_1}\left(R_s,y_{reg}\right)+\nu L_b\left(R_s,R_t,y_{reg}\right)\end{array}$$

其中$m$是margin；$y_{reg}$ 是回归的gtlabel； $R_s$是student模型的回归输出； $R_t$是teacher模型的回归输出； $\nu$是权重参数，$L_{s{L}_1}$是Faster RCNN中的L1 损失函数。

Hint Learning with Feature Adaptation

论文《Fitnets: Hints for thin deepnets》表明将teacher网络中的中间表达作为hint能够帮助训练过程，并且提高student模型的最后性能。假设$Z$是teacher网络中我们选择作为hint的中间表达层，$V$是student网络中导向层（guided layer）的输出，用L2距离来表示两者之间的差异。
$$L_{Hint}\left(V,Z\right)=\Vert V-Z{\Vert }_2^2$$

但是在此论文中，作者使用的是L1损失函数。当应用hint learning时，则需要teacher和student网络相关联的层有相同的神经元，所以为了匹配hint和guided层的通道数，作者在guided 层之后增加了一个调整层。当hint和guided层都是卷积层，跳帧层则采用了$1\times 1$的卷积层；当hint和guided层都是全连接层时，调整层也是全连接层。

$$L_{Hint}\left(V,Z\right)=\Vert V-Z{\Vert }_1$$

Result

Table 1 中显示了4个student模型（VGG16，VGGM，AlexNet，Tucker）在PASCAL，COCO，KITTI和ILSVRC数据集上的mAP值。第二列模型的信息中展示模型的参数量和每张图片在GPU上的运行时间。其中带有‘-’的行没有使用蒸馏模型，可作为标准进行对比。从表中可以看出，越复杂的模型作为teacher能够帮助student模型表现更好。

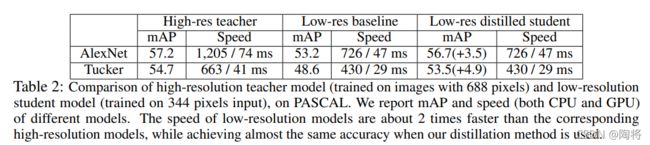
除此之外，论文中还发现了一种新的teacher-student模式，student和teacher网络结构一样，但是student网络的输入是按比例缩小的，teacher网络的输入保持高分辨率。图像的分辨率能够影响目标检测的性能。当使用低质量图片时，能够减少卷积资源和减速计算。Table 2 中展示了在PASCAL VOC 数据集上，teacher模型的输入保持原分辨率，将原分辨率缩放一半作为student模型的输入时的模型效果。我们可以看出，经过蒸馏后的低分辨率student模型的mAP和teacher模型的mAP相差一个点左右，但是速度在CPU/GPU上都将近提升了一倍。

Distilling Object Detectors with Fine-grained Feature Imitation

github代码地址：Distilling-Object-Detectors

hint learning中通过最小化teacher 和student模型高层次特征之间的差异提高student模型的性能。但是论文中发现在检测模型中直接应用hint learning会降低性能。这是因为分类模型更加关注全局信息，检测模型更加关注和gt物体重叠的区域信息。尤其是对目标检测，背景实例是多种多样的，直接应用所有的特征将不可避免地引入不关注区域的大量噪音。

检测模型关注的是局部目标区域，受知识蒸馏思想指引，我们直观认为响应在目标附近近anchor位置特征的差异性会会携带帮助检测模型检测出目标实例的信息。近物体anchor位置的特征差异揭示了学习型teacher模型是如何趋向于通用。teacher对拥挤物体交叉点的反映和对物体位置的反应反映除了teacher如何分离和检测那些拥挤的物体的。

此篇论文开发出了一个简单易用的细粒度特征模拟方法，利用teacher模型对近目标anchor位置的特征差异 （the discrepancy of feature response on the near object anchor location）提取复杂监测模型中的信息。下图是论文思想的展示。

Imitation region estimation

近目标anchor位置形成了每一个物体的局部特征区域。为了能够定义和学习这个局部特征区域，论文中利用gt bbox和anchor priors为每一个图像计算这些区域并记为mask $I$，并且通过一个阈值参数$\phi$控制区域大小。

对于每一个gt box，我们计算它和所有anchor的IOU，得到一个$W\times H\times K$ 大小的IOU图$m$，其中$W$和$H$表示特征图的宽和高，$K$表示$K$个预设anchor box。接着我们找到最大的IOU值$M=max\left(m\right)$，乘以阈值参数$\phi$获得过滤阈值$F=\phi \ast M$。然后我们将IOU图上大于$F$的位置保存下来，并使用或操作把它们结合起来得到大小为$W\times H$ 的mask。最后，循环完所有的gt box，并且结合所有的masks，得到最终版的细粒度模仿mask（fine-grained imitation ）$I$。

当$\phi =0$时，生成的mask包括特征图上所有的位置，当$\phi =1$时，则没有任何位置信息。所以可以通过改变$\phi$得到不同的imitation mask。

为了探索$\phi$的作用，不断变换阈值参数$\phi$， 分别在0.5X和0.25X的student模型上进行实验验证，并画出不同$\phi$下模型性能折线图。如下图所示，从图中看出，随着$\phi$值得增大，模型mAP值也随之增高，当$\phi =0.5$时到达顶点，并下降。

为了能够更好地理解imitation mask，论文利用toy检测模型在输入图像上可视化一些masks $I$。下图显示了不同尺寸的imitation masks并且覆盖上输入图像上。在下图的6张图片上，子图（a）是原图，子图（b）（c）（d）分别由$\phi =0.2$ ,$\phi =0.5$ 和$\phi =0.8$生成。子图（e）和（f）分别是使用固定的阈值参数$F=0.5$和$F=0.8$。从图中可以看出，当$F=0.5$时，一些物体已经开始消失了，当$F=0.8$时，几乎所有的imitation mask都消失了。

Fine-grained feature imitation

为了能够开展模仿，论文中在相应student模型后在计算student和teacher特征距离之前添加了一个全卷积调整层。添加调整层有两个原因。第一：student模型特征通道数目可能与teacher模型的特征数目不匹配，添加的调整层可以调整学生模型通道数目以便于计算特征距离。第二：当student模型和teacher模型具有相匹配的特征时，迫使student模型接近teacher模型的特征直接导致最小化收益。

下面具体介绍特征模仿细节。定义student模型guided 特征图为$s$，相应的teacher模型特征图为$t$。定义尺寸为$W\times H$的特征图上每一个近目标anchor位置为$i,j$，那么训练studnet模型最小化如下目标函数去学习teacher检测模型的知识。

$$l=\sum _{c=1}^C{\left(f_{adap}{\left(s\right)}_{ijc}-t_{ijc}\right)}^2$$

加上imitation mask $I$，蒸馏目标函数定义如下所示，其中$N_p={\sum }_{i=1}^W{\sum }_{j=1}^H{I}_{ij}$是mask中的正例数目，$f_{adap}\left(\cdot \right)$是调整函数

$$L_{imitation}=\frac{1}{2N_p}\sum _{i=1}^W\sum _{j=1}^H\sum _{c=1}^C{I}_{ij}{\left(f_{adap}{\left(s\right)}_{ijc}-t_{ijc}\right)}^2$$

蒸馏目标函数，再加上原检测模型训练目标函数$L_{gt}$，那么studnet模型的总的目标函数如下定义，其中$\lambda$是模拟权重平衡参数。

$$L=L_{gt}+\lambda L_{imitation}$$

imitation with Faster RCNN

halved student model

使用backbone网络为Resnet101的Faster RCNN为teacher模型，对每一层（包括全连接层）的通道数减半构建student 模型。我们在Pascal VOC07数据集上进行实验。从下表中我们看出减半的student模型的mAP低于teacher模型8%，但是student模型加上模仿操作之后，mAP提升3.8%。从实验结果中，也可以看出论文中提出的方法能够帮助student模型从teacher模型中学校到知识。

Shallow studnet network

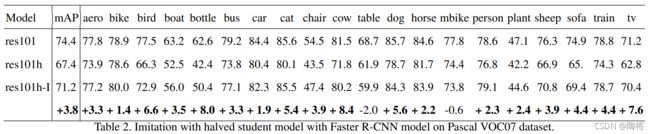
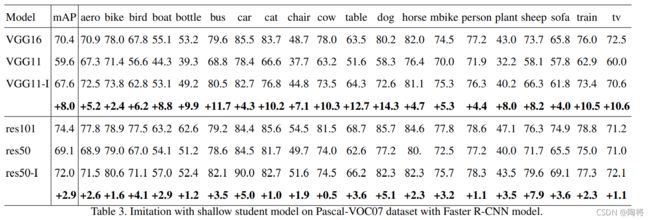
选择和teacher模型相似的结构作为student模型的backbone。论文中做了两组实验，第一组是VGG16为backbone的Faster RCNN作为teacher模型，VGG11为backbone的Faster RCNN作为student模型。第二组是Resnet101为backbone的Faster RCNN作为teacher模型，Resnet50为backbone的Faster RCNN作为student模型。结果如下图所示。可以从图中看出，两组模仿模型都有所提高，特别是第一组实验，提高了8%，将studnet模型和teacher模型两者之间mAP的差异从10.8%缩小到2.8%。

multi-layer imitation

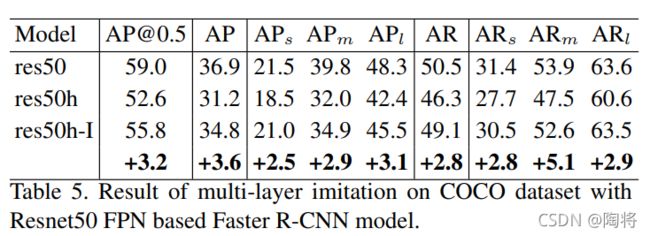
上两种实验都是在单层的特征图上，论文还在多层特征图上（FPN）进行实验。带FPN的Faster在不同尺寸anchor的不同层上进行区域提取。计算每一层相对应的anchor的imitation region，并且让student模型模仿每一层的特征。teacher模型是基于Resnet50 FPN的Faster RCNN，student模型是上述第一种 halved student model。实验结果如下所示。在COCO数据集上，模拟studnet模型比原studnet模型mAP提高了3.2%。

参考

1. Distilling the Knowledge in a Neural Network
2. 模型压缩 | 知识蒸馏经典解读
3. Knowledge Distillation
4. Learning Efficient Object Detection Models with Knowledge Distillation
5. Distilling Object Detectors with Fine-grained Feature Imitation