【实战 python】 第4章 决策树—— 信息增益 ID3（连续值处理）习题4.3 python实现

4.3 试编程实现基于信息熵进行划分选择的决策树算法，并为表4.3中数据生成一棵决策树。

理论知识：笔记（四）机器学习（周志华）第4章 决策树

Homework4.3-ID3Model.py

#!/usr/bin/python
# -*- coding: utf-8 -*-
# @Time    : 2019/8/20 9:00
# @Author  : Cabbage
# @project : decisionTree
# @FileName: Homework4.3-ID3Model.py
# @Blog    ：https://blog.csdn.net/lzbmc

from numpy import *
import pandas as pd
from math import log
import operator
import pickle  # python序列化对象，这里序列化保存树结构的字典对象

# 计算数据集的香农熵
def calcShannonEnt(dataSet):
    numEntries = len(dataSet)  # 分母：训练数据的数量
    labelCounts = {}  # 分子：数据集或者每个子集中，每个类别（好瓜、坏瓜）出现的次数
    # 给所有可能分类创建字典
    for featVec in dataSet:
        currentLabel = featVec[-1]  # 取最后一列数据
        if currentLabel not in labelCounts.keys():  # 第一次出现时先给它初始值0
            labelCounts[currentLabel] = 0
        labelCounts[currentLabel] += 1
    shannonEnt = 0.0
    # 以2为底数计算香农熵
    for key in labelCounts:
        prob = float(labelCounts[key]) / numEntries
        shannonEnt -= prob * log(prob, 2)  # Ent=-(∑pk㏒pk)  --> Ent减每一个结果 P75(4.1)
    return shannonEnt


# 对离散变量划分数据集，取出该特征取值为value的所有样本
def splitDataSet(dataSet, axis, value):
    retDataSet = []
    for featVec in dataSet:
        if featVec[axis] == value:  # 判断此列axis的值是否为value
            reducedFeatVec = featVec[:axis]  # 此行数据的前axis列
            reducedFeatVec.extend(featVec[axis + 1:])  # axis列之后的数据
            retDataSet.append(reducedFeatVec)  # 注意extend与append的区别。
            # 三句合写为一句
            # retDataSet.append(featVec[:axis] + featVec[axis + 1:])
            # a、b为例，extend,append是在a原地址操作，改变的是a。
            # extend：去掉列表b最外层的[]，然后追加到a。append：将整个列表b作为一个值来添加。
            # +：新的变量c来实现相加，相加的过程和extend一样，但不是在被加的对象的地址上操作的。
    return retDataSet


# 对连续变量划分数据集——二分法。不大于或者大于value的样本分别保存，进行划分
# direction规定划分的方向，决定是划分出小于value的数据样本还是大于value的数据样本集
def splitContinuousDataSet(dataSet, axis, value, direction):
    retDataSet = []
    for featVec in dataSet:
        if direction == 0:
            if featVec[axis] > value:
                retDataSet.append(featVec)  # 连续型特征和特征值都不删除
        else:
            if featVec[axis] <= value:
                retDataSet.append(featVec)
    return retDataSet


# 选择最好的数据集划分方式
def chooseBestFeatureToSplit(dataSet, labels):
    numFeatures = len(dataSet[0]) - 1  # 特征的数目，最后一列是类别
    baseEntropy = calcShannonEnt(dataSet)  # 经验熵 Ent(D)
    bestInfoGain = 0.0  # 最优的信息增益值。
    bestFeature = -1  # 最优的Feature编号
    bestSplitDict = {}  # key:value = {连续型特征标签:最优划分点}
    # bestSplitValue = None  # 连续型特征的最优划分点
    for i in range(numFeatures):
        featList = [example[i] for example in dataSet]  # 获取第i列(第i特征)下的所有数据，存到列表中

        # 对连续型特征进行处理
        # 为每一个连续型特征寻找最优划分点，并计算在最优划分点时的信息增益
        if type(featList[0]).__name__ == 'float' or type(featList[0]).__name__ == 'int':  # 判断当前属性是否为连续型.等价于type(featList[0]) == float:
            # 产生n-1个候选划分点
            sortfeatList = sorted(featList)  # 二分法：先对属性值从小到大进行排序
            splitList = []
            for j in range(len(sortfeatList) - 1):  # 每一个划分点是相邻属性值的平均
                splitList.append((sortfeatList[j] + sortfeatList[j + 1]) / 2.0)

            bestSplitEntropy = 10000
            slen = len(splitList)  # 划分点个数
            # 求用第j个候选划分点划分时，得到的信息熵，并记录最佳划分点
            for j in range(slen):
                value = splitList[j]  # 划分点的值value <=value,>value
                newEntropy = 0.0  # 创建一个临时的信息熵，用来作比较
                subDataSet0 = splitContinuousDataSet(dataSet, i, value, 0)  # 划分数据集  >value
                subDataSet1 = splitContinuousDataSet(dataSet, i, value, 1)  # <=value
                # print(subDataSet0)
                # print(subDataSet1)

                prob0 = len(subDataSet0) / float(len(dataSet))  # >value的比例
                prob1 = len(subDataSet1) / float(len(dataSet))
                newEntropy = prob0 * calcShannonEnt(subDataSet0) + prob1 * calcShannonEnt(subDataSet1)  # P75(4.2)的减数
                if newEntropy < bestSplitEntropy:  # 越小越好 因为Ent(D)固定-newEntropy
                    bestSplitEntropy = newEntropy
                    bestSplit = j
            # 用字典记录当前特征(属性)的最佳划分点
            bestSplitDict[labels[i]] = splitList[bestSplit]
            infoGain = baseEntropy - bestSplitEntropy  # 当前连续型特征最优划分点的信息增益

        # 对离散型特征进行处理
        else:
            uniqueVals = set(featList)  # 特征值去重
            newEntropy = 0.0
            # 针对每个特征值，划分数据集 并 计算各子集的信息熵
            for value in uniqueVals:
                subDataSet = splitDataSet(dataSet, i, value)  # 第i个特征取值为value对应的每个样本组成的数据集
                prob = len(subDataSet) / float(len(dataSet))  # Dv/D
                newEntropy += prob * calcShannonEnt(subDataSet)  # prob*信息熵，累加每一个特征值value的
            infoGain = baseEntropy - newEntropy  # 离散型特征的 信息增益

        #  比较每一个特征的信息增益，选择最大的。 例如纹理
        if infoGain > bestInfoGain:
            bestInfoGain = infoGain
            bestFeature = i

    # 返回：最优划分特征所在的列，和连续型{特征标签:最优划分点}
    return bestFeature, bestSplitDict


# 采用多数表决（投票）的方法决定该叶子结点的分类。
# 例如：敲声=沉闷的数据中，好瓜:2，坏瓜:3-->敲声=沉闷是坏瓜
def majorityCnt(classList):
    classCount = {}  # 存储每个类别标签出现的频率 key:value = {属性值:出现的次数}
    for vote in classList:
        if vote not in classCount.keys():
            classCount[vote] = 0
        classCount[vote] += 1
    sortedClassCount = sorted(classCount.items(), key=operator.itemgetter(1), reverse=True)  # 字典按1(value)进行排序，变成列表
    # [(k,v), (),...]
    return sortedClassCount[0][0]


# 主程序，递归产生决策树
def createTree(dataSet, labels, data_full, labels_full):
    classList = [example[-1] for example in dataSet]  # 数据集最后一列的数据,类别
    if classList.count(classList[0]) == len(classList):  # 一、如果样本都属于同一类，例如都是好瓜，就没必要再分类了。
        return classList[0]
    if len(dataSet[0]) == 1:  # 二、所有特征都用完了，但类别标签仍然不是唯一的,返回出现次数最多的类别
        return majorityCnt(classList)

    bestFeat, bestSplitDict = chooseBestFeatureToSplit(dataSet, labels)  # 选择最优划分特征  bestFeat:最优特征所在索引
    if bestFeat == -1:  # 三、没有选出最优划分特征，返回出现次数最多的类别
        return majorityCnt(classList)

    bestFeatLabel = labels[bestFeat]  # 列对应的特征标签。
    # 1、最优划分特征是离散型
    if type(dataSet[0][bestFeat]).__name__ == 'str':
        # 注意：这里不能在if上面，全局变量的话对于连续型特征的key会不相等，例如密度和密度<=0.381
        myTree = {bestFeatLabel: {}}  # 初始化myTree，使用特征标签创建树，多级字典的形式展现树
        featValues = [example[bestFeat] for example in dataSet]  # 最优特征列对应的取值
        uniqueVals = set(featValues)  # 特征值去重，有几个不同取值  dataSet随着数据集划分会变小 {'青绿', '乌黑'}

        # dataSet随着数据集的划分，子集中包含的属性值会减少，比如纹理：清晰，稍糊，模糊。
        # 在清晰下的子集中5个样本，最优特征为色泽，实际色泽有青绿、乌黑、浅白，这5个样本没有浅白，会造成缺失。
        # 因此，需要一个包含全部数据的data_full，来获取所有特征值。
        # 因为，在划分数据时，删除最优划分特征所对应的列，导致在dataSet和data_full 中对应的列（bestFeat）不同
        # 所以，先找到最优特征对应的标签即bestFeatLabel，然后标签对应在data_full列，最后得到该列对应的不同特征值。
        bestFeatIndexInFull = labels_full.index(bestFeatLabel)  # list.index(key)：返回key出现的第一个位置
        featValuesFull = [example[bestFeatIndexInFull] for example in data_full]
        uniqueValsFull = set(featValuesFull)  # 这一特征在全部数据集中的所有特征值
        # print(uniqueVals, 'uniqueValsFull:', uniqueValsFull)  # {'浅白', '青绿', '乌黑'}

        del (labels[bestFeat])  # 离散型特征选择完之后就不再作为划分特征
        for value in uniqueValsFull:  # 例如最优特征：纹理；uniqueVals：清晰，稍糊，模糊
            if value in uniqueVals:
                subLabels = labels[:]  # 去掉最优划分特征之后，剩下的特征集
                valueDataSet = splitDataSet(dataSet, bestFeat, value)  # 特征值为value的所有数据
                myTree[bestFeatLabel][value] = createTree(valueDataSet, subLabels, data_full, labels_full)
                # print('===', myTree)  # 先输出嵌套的最里层
            else:
                myTree[bestFeatLabel][value] = majorityCnt(classList)  # 子集没有的特征值，返回出现次数最多的类别

    # 2、连续型特征，不删除
    else:
        bestSplitValue = bestSplitDict[bestFeatLabel]  # 特征对应的最优划分点
        bestFeatLabel = labels[bestFeat] + '<=' + str(bestSplitValue)  # 密度变为：密度<=0.381
        myTree = {bestFeatLabel: {}}  # 初始化myTree，使用特征标签创建树，多级字典的形式展现树

        subDataSet0 = splitContinuousDataSet(dataSet, bestFeat, bestSplitValue, 0)  # >value
        subDataSet1 = splitContinuousDataSet(dataSet, bestFeat, bestSplitValue, 1)  # <=value
        myTree[bestFeatLabel]['否'] = createTree(subDataSet0, labels, data_full, labels_full)
        # print('连续型否：', myTree)  # 先输出最底层的键值对，作为上一层的value
        myTree[bestFeatLabel]['是'] = createTree(subDataSet1, labels, data_full, labels_full)
        # print('连续型是：', myTree)
    return myTree


# 使用pick模块存储决策树
def storeTree(inputTree, filename):  # 序列化的对象可以在磁盘上保存，需要时读取
    fw = open(filename, 'wb')  # 'w'TypeError: write() argument must be str, not bytes 改成‘wb’
                            # pickle存储方式默认是二进制方式 ,要以二进制方式打开文件
    pickle.dump(inputTree, fw)
    fw.close()

# 读取决策树模型
def grabTree(filename):
    fr = open(filename, 'rb')
    return pickle.load(fr)


if __name__ == "__main__":
    df = pd.read_csv('data/Watermelon3.0')
    data = df.values[:, 1:].tolist()  # 获取内部数据，保存成列表格式
    data_full = data[:]  # 复制一份,为了避免特征划分导致特征对应数据的缺失
    labels = df.columns.values[1:-1].tolist()  # 表头：特征
    labels_full = labels[:]  # 复制一份

    myTree = createTree(data, labels, data_full, labels_full)
    print('myTree:', myTree)

    filename = './DTModel/ID3Model'
    storeTree(myTree, filename)
    #
    # loadModel = grabTree(filename)
    # print(loadModel)

   

输出结果：
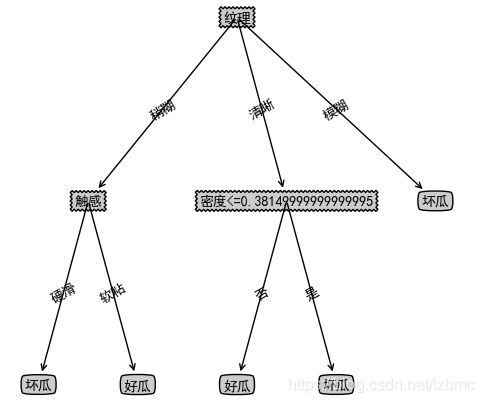
myTree: {‘纹理’: {‘稍糊’: {‘触感’: {‘硬滑’: ‘坏瓜’, ‘软粘’: ‘好瓜’}}, ‘模糊’: ‘坏瓜’, ‘清晰’: {‘密度<=0.38149999999999995’: {‘否’: ‘好瓜’, ‘是’: ‘坏瓜’}}}}

Homework4.3-ID3Plt.py

#!/usr/bin/python
# -*- coding: utf-8 -*-
# @Time    : 2019/8/22 20:36
# @Author  : Cabbage
# @project : decisionTree
# @FileName: Homework4.3-ID3Plt.py
# @Blog    ：https://blog.csdn.net/lzbmc

import matplotlib.pyplot as plt
import pickle

# 定义文本框和箭头格式。两种格式的文本框分别代表叶结点和其他节点。
decisionNode = dict(boxstyle="sawtooth", fc="0.8")  # 决策树根结点和内部结点的属性。
# boxstyle="sawtooth" ：文本框的边缘是波浪线，fc="0.8" ：颜色深度。可以写为decisionNode={boxstyle:'sawtooth',fc:'0.8'}
leafNode = dict(boxstyle="round4", fc="0.8")
arrow_args = dict(arrowstyle="<-")  # 箭头样式
# 下面两句解决中文乱码问题
plt.rcParams['font.sans-serif'] = [u'SimHei']
plt.rcParams['axes.unicode_minus'] = False


# 计算树的叶子节点数量，以确定x轴的长度
def getNumLeafs(myTree):
    numLeafs = 0
    firstStr = list(myTree.keys())[0]  # dict.keys()返回的不在是list类型了，也不支持索引。先转换成list
    # firstStr = myTree.keys()[0]
    secondDict = myTree[firstStr]
    for key in secondDict.keys():
        if type(secondDict[key]).__name__ == 'dict':  # {'纹理': {'模糊': '坏瓜', '稍糊': {'触感': {'软粘': '好瓜',}}}}
            numLeafs += getNumLeafs(secondDict[key])  # 只要value字典，就一直递归，直到不是(模糊: 坏瓜),此时是叶结点+1
        else:
            numLeafs += 1
    return numLeafs


# 计算树的最大深度，以确定y轴的长度
def getTreeDepth(myTree):
    maxDepth = 0
    firstStr = list(myTree.keys())[0]
    secondDict = myTree[firstStr]
    for key in secondDict.keys():
        if type(secondDict[key]).__name__ == 'dict':  # 如果value是字典就加以，直到不是，取最大
            thisDepth = 1 + getTreeDepth(secondDict[key])
        else:
            thisDepth = 1
        if thisDepth > maxDepth:
            maxDepth = thisDepth
    return maxDepth


# 绘制带箭头的注解
def plotNode(nodeTxt, centerPt, parentPt, nodeType):
    createPlot.ax1.annotate(nodeTxt, xy=parentPt, xycoords='axes fraction', \
                            xytext=centerPt, textcoords='axes fraction', va="center", ha="center", \
                            bbox=nodeType, arrowprops=arrow_args)


# nodeTxt为要显示的文本，centerPt为文本的中心点，parentPt为箭头指向文本的点，xy是箭头尖的坐标，xytest设置注释内容显示的中心位置
# xycoords和textcoords是坐标xy与xytext的说明（按轴坐标），若textcoords=None，则默认textcoords与xycoords相同，若都未设置，默认为data
# va/ha设置节点框中文字的位置，va为纵向取值为(u'top', u'bottom', u'center', u'baseline')，ha为横向取值为(u'center', u'right', u'left')


# 在父子节点间 填充文本信息。也就是剪头线上的标注，在两个点坐标的中心处添加标注
def plotMidText(cntrPt, parentPt, txtString):
    xMid = (parentPt[0] - cntrPt[0]) / 2.0 + cntrPt[0]
    yMid = (parentPt[1] - cntrPt[1]) / 2.0 + cntrPt[1]
    # print(xMid, yMid, txtString)
    createPlot.ax1.text(xMid, yMid, txtString, va="center", ha="center", rotation=30)


# 递归函数，树的宽度来计算判断节点的位置，是放在所有叶子节点的中间，不仅仅是它子结点的中间。
# 其中两个全局变量plotTree.xOff和plotTree.yOff，用于追踪已绘制的节点位置，并放置下个节点的恰当位置
def plotTree(myTree, parentPt, nodeTxt):  # nodeTxt:key
    numLeafs = getNumLeafs(myTree)
    depth = getTreeDepth(myTree)
    firstStr = list(myTree.keys())[0]
    cntrPt = (plotTree.xOff + (1.0 + float(numLeafs)) / 2.0 / plotTree.totalW, plotTree.yOff)  # 按照叶子结点个数划分x轴(0.5, 1.0)
    # print('cntrPt:', cntrPt)
    plotMidText(cntrPt, parentPt, nodeTxt)  # 箭头线上文本
    plotNode(firstStr, cntrPt, parentPt, decisionNode)  # 判断结点
    secondDict = myTree[firstStr]
    plotTree.yOff = plotTree.yOff - 1.0 / plotTree.totalD  # 采用的自顶向下的绘图，需要依次递减Y坐标；按比例减少plotTree.yOff
    for key in secondDict.keys():  # value为字典，继续递归
        if type(secondDict[key]).__name__ == 'dict':
            plotTree(secondDict[key], cntrPt, str(key))
        else:  # 为叶子结点
            plotTree.xOff = plotTree.xOff + 1.0 / plotTree.totalW  # x方向计算节点坐标
            plotNode(secondDict[key], (plotTree.xOff, plotTree.yOff), cntrPt, leafNode)  # 绘图，叶子结点
            plotMidText((plotTree.xOff, plotTree.yOff), cntrPt, str(key))  # 添加文本信息
    plotTree.yOff = plotTree.yOff + 1.0 / plotTree.totalD  # 下次重新调用时恢复y


# 主函数
def createPlot(inTree):
    fig = plt.figure(1, facecolor='white')  # 新建一个画布，背景设置为白色的
    fig.clf()  # 清空绘图区
    axprops = dict(xticks=[], yticks=[])
    createPlot.ax1 = plt.subplot(111, frameon=False, **axprops)  # frameon表示是否绘制坐标轴矩形
    plotTree.totalW = float(getNumLeafs(inTree))  # 树的宽度#全局变量宽度 = 叶子数
    plotTree.totalD = float(getTreeDepth(inTree))  # 树的深度#全局变量高度 = 深度
    plotTree.xOff = -0.5 / plotTree.totalW  # 例如绘制3个叶子结点，坐标应为1/3,2/3,3/3
    plotTree.yOff = 1.0  # 但这样会使整个图形偏右因此初始的，将x值向左移一点。
    plotTree(inTree, (0.5, 1.0), '')
    plt.show()


if __name__ == '__main__':
    filename = './DTModel/ID3Model'
    fr = open(filename, 'rb')
    tree = pickle.load(fr)
    createPlot(tree)

结果：

Homework4.3-ID3ClassifyTest.py

#!/usr/bin/python
# -*- coding: utf-8 -*-
# @Time    : 2019/8/23 19:41
# @Author  : Cabbage
# @project : ML
# @FileName: Homework4.3-ID3ClassifyTest.py
# @Blog    ：https://blog.csdn.net/lzbmc

def classify(inputTree, featLabels, testVec):
    firstStr = list(inputTree.keys())[0]  # 根结点 key
    firstLabel = firstStr[:]
    secondDict = inputTree[firstStr]  # 剩下的值

    if '<=' in firstStr:  # 连续型特征在模型保存时key变了
        firstStr = firstStr.split('<=')[0]  # 得到对应标签，需要拆开

    featIndex = featLabels.index(firstStr)
    for key in secondDict.keys():
        # 离散型特征
        if type(testVec[featIndex]).__name__ == 'str':
            if testVec[featIndex] == key:
                if type(secondDict[key]).__name__ == 'dict':  # 字典，递归继续往下走
                    classLable = classify(secondDict[key], featLabels, testVec)
                else:  # 叶子结点，返回结果
                    classLable = secondDict[key]
        # 连续型特征
        else:
            value = float(firstLabel.split('<=')[1])
            if testVec[featIndex] > value:  # 大于判断条件，特征对应的特征值为否 {'密度<=0.381': {'否': '好瓜', '是': '坏瓜'}
                if type(secondDict['否']).__name__ == 'dict':
                    classLable = classify(secondDict['否'], featLabels, testVec)
                else:
                    classLable = secondDict['否']
            else:
                if type(secondDict['是']).__name__ == 'dict':
                    classLable = classify(secondDict['是'], featLabels, testVec)
                else:
                    classLable = secondDict['是']

    return classLable


labels = ['色泽', '根蒂', '敲声', '纹理', '脐部', '触感', '密度', '含糖率']
testData = ['浅白', '蜷缩', '浊响', '清晰', '凹陷', '硬滑', 0.5, 0.002]
tree = {'纹理': {'清晰': {'密度<=0.38149999999999995': {'否': '好瓜', '是': '坏瓜'}}, '稍糊': {'触感': {'软粘': '好瓜', '硬滑': '坏瓜'}},
               '模糊': '坏瓜'}}
testClass = classify(tree, labels, testData)
print(testClass)

结果：好瓜