基于python的灰色预测模型
灰色系统
我们称信息完全未确定的系统为黑色系统,称信息完全确定的系统为白色系统,灰色系统就是这介于这之间,一部分信息是已知的,另一部分信息是未知的,系统内各因素间有不确定的关系。
特点
- 用灰色数学处理不确定量,使之量化。
- 充分利用已知信息寻求系统的运动规律。
- 灰色系统理论能处理贫信息系统。
直接上代码
首先引入所需要的库
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
data = pd.read_excel("E:/桌面/灰色预测.xlsx",sheet_name=1)
list1 = data["序列"]
tlist1 = [2014,2015,2016,2017,2018]完整代码。
编写函数GM11(x,n)
fy = []
def GM11(x,n):
'''
灰色预测
x:序列,numpy对象
n:需要往后预测的个数
'''
x1 = x.cumsum()#一次累加
z1 = (x1[:len(x1) - 1] + x1[1:])/2.0#紧邻均值
z1 = z1.reshape((len(z1),1))
B = np.append(-z1,np.ones_like(z1),axis=1)
Y = x[1:].reshape((len(x) - 1,1))
#a为发展系数 b为灰色作用量
[[a],[b]] = np.dot(np.dot(np.linalg.inv(np.dot(B.T, B)), B.T), Y)#计算待估参数
result = (x[0]-b/a)*np.exp(-a*(n-1))-(x[0]-b/a)*np.exp(-a*(n-2)) #预测方程
S1_2 = x.var()#原序列方差
e = list()#残差序列
for index in range(1,x.shape[0]+1):
predict = (x[0]-b/a)*np.exp(-a*(index-1))-(x[0]-b/a)*np.exp(-a*(index-2))
e.append(x[index-1]-predict)
print(predict) #预测值
fy.append(predict)
print("后验差检验")
S2_2 = np.array(e).var()#残差方差
C = S2_2/S1_2#后验差比
if C<=0.35:
assess = '后验差比<=0.35,模型精度等级为好'
elif C<=0.5:
assess = '后验差比<=0.5,模型精度等级为合格'
elif C<=0.65:
assess = '后验差比<=0.65,模型精度等级为勉强'
else:
assess = '后验差比>0.65,模型精度等级为不合格'
#预测数据
predict = list()
for index in range(x.shape[0]+1,x.shape[0]+n+1):
predict.append((x[0]-b/a)*np.exp(-a*(index-1))-(x[0]-b/a)*np.exp(-a*(index-2)))
predict = np.array(predict)
return {
'a':{'value':a,'desc':'发展灰数'},
'b':{'value':b,'desc':'控制灰数'},
'predict':{'value':result,'desc':'第%d个预测值'%n},
'C':{'value':C,'desc':assess},
'predict':{'value':predict,'desc':'往后预测%d个的序列'%(n)},
}
if __name__ == "__main__":
data = np.array(list1)
x = data[0:5]#输入数据
#y = data[0:]#需要预测的数据
result = GM11(x,1)
predict = result['predict']['value']
predict = np.round(predict,1)
#print('真实值:',x)
print('预测值:',predict)
print(result)
print("残差检验")
a = []
for i in range(5):
a.append(abs(fy[i]-list1[i]))
print('%.5f%%' % ((abs(fy[i]-list1[i]))/list1[i]))
print("关联度检验")
c= []
for i in range(5):
b = (min(a)+0.5*max(a))/(abs(a[i])+0.5*max(a))
c.append(b)
print("ρ = 0.5 关联度为:",np.mean(c))
#print(y)
print(predict)
fy.append(3.8)检验
后验差检验,关联度检验,残差检验。解释(上面代码已经包含)
print("后验差检验")
S2_2 = np.array(e).var()#残差方差
C = S2_2/S1_2#后验差比
if C<=0.35:
assess = '后验差比<=0.35,模型精度等级为好'
elif C<=0.5:
assess = '后验差比<=0.5,模型精度等级为合格'
elif C<=0.65:
assess = '后验差比<=0.65,模型精度等级为勉强'
else:
assess = '后验差比>0.65,模型精度等级为不合格'后验差检验检验结果判定
关联度与残差检验。
print("残差检验")
a = []
for i in range(5):
a.append(abs(fy[i]-list1[i]))
print('%.5f%%' % ((abs(fy[i]-list1[i]))/list1[i]))
print("关联度检验")
c= []
for i in range(5):
b = (min(a)+0.5*max(a))/(abs(a[i])+0.5*max(a))
c.append(b)
print("ρ = 0.5 关联度为:",np.mean(c))关联度检验结果大于0.6即可。
输出结果。
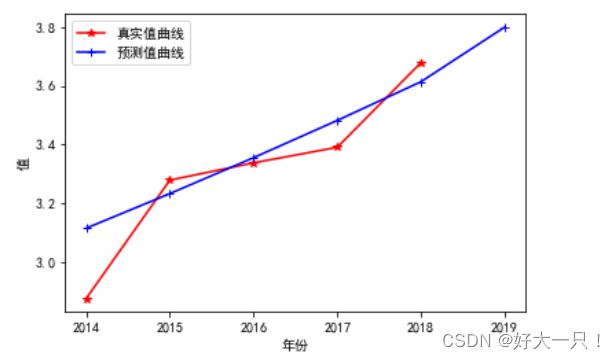
对结果与源数据进行对比
#作图
import numpy as np
import matplotlib.pyplot as plt
x1 = np.array([2014,2015,2016,2017,2018])
y1 = np.array(x)
x2 = np.array([2014,2015,2016,2017,2018,2019])
y2 = np.array(fy)
plt.plot(x1,y1,'r*-',label='真实值曲线') #真实值
plt.plot(x2,y2,'b+-',label='预测值曲线') #预测值
plt.xlabel('年份')
plt.ylabel('值')
plt.legend()
plt.plot()
plt.show()利用python对灰色系统进行预测适用于短期预测,对长期预测效果并不是很好。若需要长期预测可使用ARIMA(p,d,q)模型。